一种新型两自由度永磁电机动力学模型*

2020-11-27贾鹏志张永顺

机电工程技术 2020年10期

贾鹏志，张永顺

（大连理工大学精密与特种加工教育部重点实验室，辽宁大连 116024）

0 引言

在航空航天以及医学工程等领域中，对可实现多自由度运动的高集成机器人手腕关节装置的需求与日俱增。传统上，多自由度手腕关节通常是由多个单自由度关节串联而成，通过协调各关节多台电机的转动来合成多自由度手腕关节的侧摆、俯仰和自转三自由度运动。该类型手腕存在机械结构复杂、不紧凑、运动不解耦、传动精度低、柔顺与变刚度控制困难等缺点[1]。针对上述问题，研究者渴望能够开发直接实现多自由度驱动的紧凑电机装置，以提高多自由度机器人手腕装置的综合性能，尤其是消除电机与减速器构成驱动单元的反向自锁特性，希望能够便利地实现柔顺与变刚度控制。随着稀土永磁材料的不断发展，结合球形电机结构在多维运动方面的优越性，多自由度永磁式球形电动机已经成为国内外研究热点[2]。

英国学者威廉姆斯和莱斯维[3]设计了一种两自由度球形电机；美国乔治亚大学的Kok-meng Lee等[4-5]基于变磁阻的思想设计了一种感应电机，并进行了一系列的后续研究；新加坡南洋理工大学的学者[6-7]研究了一种直流球形永磁电机。

中国多自由度永磁电机的研究工作始于20世纪80年代后期，虽然相对较晚，但也取得了一些具有一定影响的研究成果。如合肥工业大学的王群京等[8]提出了一种步进式永磁球形电机；天津大学[9-10]将海尔贝克阵列性质的永磁体引入到球形电机设计，所研制的直流永磁球形电机包含海尔贝克阵列永磁体以及三层定子线圈；北京航空航天大学[11]联合研制了一种新型球形电机，包含8个永磁体磁极以及24个定子线圈。

迄今为止，多自由度永磁球形电机大多采用多磁极转子和多层线圈阵列定子类型基本结构。大量的永磁体磁极以及定子线圈所带来的问题便是电机内部的三维磁场环境越发复杂，精确控制难度大。多自由度永磁电机的理论和技术尚处在探索中，离实际应用还有一定的距离。

大连理工大学胶囊机器人课题组[12]研制了双半球欠驱动胶囊机器人，通过嵌入主动半球内的径向磁化永磁体与空间旋转磁场对的旋转轴线的随动效应（即双半球欠驱动胶囊机器人的轴线会追随空间旋转磁场的旋转轴线转动并最终与其基本重合的物理现象）来控制机器人轴线绕定点摆动并可于任意方向悬停。受此启发，本文将胶囊机器人轴线随动原理应用于永磁球形电机驱动原理，实现了一种新型两自由度永磁电机的结构设计与理论仿真，结果表明原理切实可行。

1 电机基本结构

两自由度永磁电机的设计主要是通过一个电机装置完成侧摆、俯仰两个运动的输出。原理上应用了永磁体在旋转磁场中的随动效应[13]；结构上利用2 个十字万向节结构替代了球面结构，实现两自由度运动的同时，避免了复杂球面的存在。

新型永磁电机的整体结构如图1 所示，大体可分为两个部分。第一部分为定子部分，即三轴正交的亥姆霍兹线圈组；第二部分为转子随动部分，包括内部十字万向节（内安装有转子永磁体）、外部万向节（安装有制动机构、阻尼机构、测量机构等）以及机架。

图1 两自由度电机整体结构示意图

1.1 亥姆霍兹线圈组

定子部分由3 组相互正交的亥姆霍兹线圈组成，亥姆霍兹线圈组中各线圈相对位置如图1所示，3对线圈轴线相互垂直且交于一点。作用是为转子永磁体提供万向旋转磁场，空间万向旋转磁场旋转轴线的方位与旋转方向是通过通入3组线圈电流反相位叠加原理实现的[14]。

1.2 转子随动部分

转子随动部分如图2所示，主要包括内部十字万向节、外部万向节及机架。内部十字万向节与外部万向节安装于机架上，显著特征是内部十字万向节和外部万向节的转动中心相同，并通过连接杆连接外部万向节和内部万向节的输出轴构成电机转动轴线，实现电机转动轴线即连杆轴线绕旋转中线的定点旋转运动，实现了电机随动部分的定点随动。外部万向节的运动可实现检测与控制，内部万向节处于自由状态，进而可以实现电机转动轴线方位的控制。下面介绍外部万向节运动的检测与控制。

1.2.1 外部万向节

如图3 所示，外部万向节主要包括内环和外环两部分，上方有一通用输出端接口。同时，还包括阻尼器、制动器、编码器，这些器件主要为了实现外部万向节的运动控制，并安装于外部万向节。内环为整体的环形结构，外环为半环形结构。

外部万向节内外环之间通过轴连接，轴与外环通过键连接，与内环通过法兰轴承连接，轴会随外环转动。内环与机架之间同样由轴连接，轴与机架之间通过法兰轴承连接，与内环通过键连接，轴随万向节内环转动。此种连接方式也为阻尼器、编码器及制动器的安装提供了方便。

外部万向节一方面可在电机工作时承受负载，另一方面也为制动机构、阻尼机构及测量机构的安装提供了额外的空间，避免了由于线圈组而导致的安装空间不足的问题。

图2 转子随动部分

（1）制动机构

制动机构为电磁制动器，如图3 所示安装于外部万向节两旋转关节处，实现对两个自由度的锁定。当电机静止时，电磁制动器实现对外部万向节的锁定，以固定转子部分方位；当电机旋转时，电磁制动器解除对万向节的锁定，以实现转子部分与万向旋转磁场的随动，即实现侧摆与俯仰转动的驱动。

图3 外部万向节

（2）阻尼机构

阻尼机构由2个阻尼器构成，如图3所示安装于外部万向节两旋转关节处，在电机进行俯仰、侧摆运动时提供阻尼，以便减缓侧摆与俯仰姿态调整时的振动。

（3）测量机构

测量机构选取2个绝对编码器，如图3所示安装于外部万向节两旋转关节处，实现对侧摆与俯仰转动2个角度的实时测量，并传输给控制系统，以实现对侧摆与俯仰角度转动的准确控制。

1.2.2 内部十字万向节

内部十字万向节结构如图4 所示，柱形壳体通过轴承安装于内部万向节环形部分上，两者共同组成一个十字万向节。十字万向节通过轴承安装于机架上。中心的柱形壳体可进行侧摆俯仰两个自由度的运动。永磁体通过轴承安装于十字万向节的柱形壳体内部，可进行自转。柱形壳体分为两部分，通过螺钉连接。柱形壳体上方安装有连接杆，两者通过螺钉固定，连接杆的另一端穿过外部万向节外环，如图2所示。

图4 内部十字万向节部分

内部万向节的作用是在耦合磁力矩的驱动下实现永磁体侧摆与俯仰自由转动，并灵活地实现与万向旋转磁场的随动，同时为永磁体提供支撑。

2 电机工作原理

电机断电时，如图2 所示，制动器对外部万向节锁定，无法进行侧摆俯仰运动。电机通电工作时的步骤如下：

第一步，根据目标位置确定空间万向旋转磁场的轴线方向，结合图1中三轴亥姆霍兹线圈组的结构及磁场强度确定线圈组所需通入的电流；

第二步，向线圈组内施加相应电流，产生相应的空间旋转磁场，图4 中永磁体在旋转磁场的作用下开始进行自转，但由于制动器对万向节两自由度的锁定无法进行侧摆、俯仰运动；

第三步，制动器通电取消对万向节的锁定，在随动效应下，永磁体轴线追随旋转磁场轴线进行侧摆、俯仰运动，同时带动双万向节同步运动；

第四步，通过图3 中编码器实时反馈位置信息，根据反馈信息，进行进一步地控制、调整；

第五步，重复第四步，当反馈信息显示达到目标位置并稳定或在目标位置以极小幅度振动，制动器断电再次对万向节锁定，固定电机方位，线圈断电，电机到达且固定于指定位置。

3 电机动力学模型建立及仿真

3.1 建立坐标系

如图5 所示，Ox0y0z0为固定坐标系，其3 条轴线分别与亥姆霍兹线圈组的3条轴线重合，且Oy0轴与外部万向节内环旋转轴线重合。赖柴坐标系初始时与固定坐标系Ox0y0z0重合，首先固定坐标系先绕Oy0旋转α角度，得到中间坐标系Ox1y0z′，再将中间坐标系 Ox1y0z′绕 Ox1轴旋转β角度，得到赖柴系Ox1y1z1。

永磁体轴线始终与赖柴系的Oz1轴重合，随赖柴系摆动且以角速度ω绕Oz1轴旋转。坐标变换中的两个角度α、β刚好与外部万向节内环同机架之间的相对转角、外部万向节内外环相对转角一致，直接对应永磁体的侧摆，俯仰角度可由编码器直接测出。

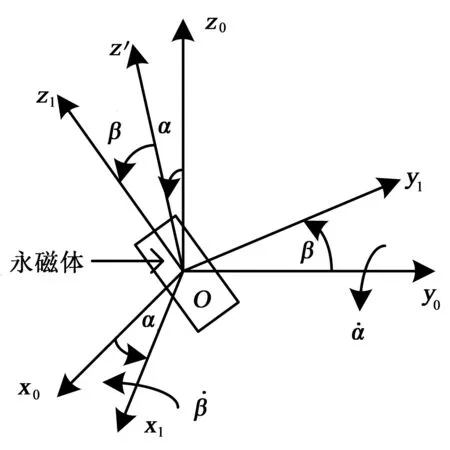
图5 赖柴系与固定坐标系关系

3.2 仿真分析

利用拉格朗日方程建立电机动力学模型后，通过Matlab/Simulink数值法计算姿态角α、β的动力学特性。假定电机本身无重力矩影响且所加负载视为质点，电机动力学方程如下：

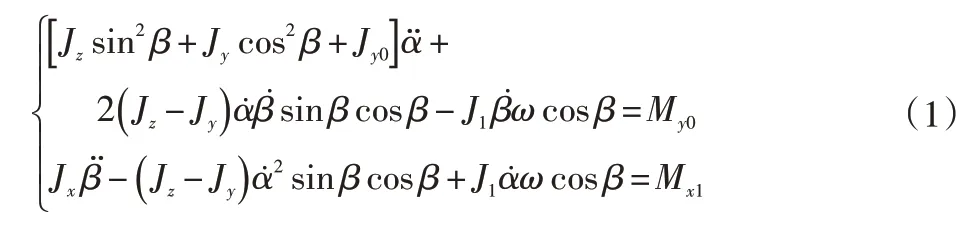
式中：α，β为2 个姿态角；Jx、Jy、Jz分别为随转子永磁体侧摆俯仰运动部分结构（包括永磁体，不包括外部万向节内环）绕赖柴系Ox1轴、Oy1轴、Oz1轴的转动惯量；J1为永磁体绕赖柴系Oz1轴转动惯量；Jy0为外部万向节内环与内部十字万向节环形部分绕Oy0轴转动惯量；My0、Mx1为Oy0轴与Ox1轴上的外力矩。

系统仿真参数如表1所示。

表1 系统仿真参数

当假定负载质量m=0.1 kg，且固定于电机输出端时，分别观察磁矢量大小及角速度大小变化对电机运动过程中姿态角的影响。

保持B=15 mT不变，减小旋转角速度时，如图6所示，虽然角速度减小了，但姿态角（α，β）最终位置相差无几。不同点在于稳定所需时间随角速度的减小而增加，且角速度越小，摆动的幅度也越大。由于重力矩的存在，最终稳定位置与预设的磁场轴线方位有小幅偏移。

保持磁场旋转角速度ω=20π rad/s 不变，改变磁矢量大小时，如图7所示，随着磁矢量的增大，最终稳定位置与磁场轴线越来越接近，B=50 mT 时几乎没有偏移。随着磁矢量的增大，姿态角抖动得也越快。

图6 磁场角速度对姿态角影响

图7 磁矢量大小对姿态角影响

图8 阻尼对姿态角影响

除了磁矢量大小及旋转角速度外，阻尼对于点击的运动也有一定影响。保持磁场旋转角速度ω=20π rad/s，磁矢量大小B=15 mT不变，改变阻尼矩系数时，如图8所示，阻尼矩系数越大，运动过程越稳定，且稳定所需时间越小。从图8中可以看出，稳定位置与磁场轴线仍有小幅偏差，但随着阻尼矩系数的变化，最终的稳定位置不发生任何变化。