用Hawgent皓骏动态数学软件提效几何开放题的教学——以“旋转求角问题”的教学为例

黄 静 胡云高 张祥婕

（[1]广西师范大学附属外国语学校 广西·桂林 541004；[2]广西师范大学数学与统计学院 广西·桂林 541006）

几何开放题是中考的热点问题，高效的几何开放题教学对培养学生思维的深刻性、全面性、严谨性、灵活性等方面具有重要作用。在传统的教学中，教师只通过枯燥的讲解和概括常见模型让学生掌握类型题，学生难以在抽象的几何情境中准确挖掘题目中隐含的条件和几何模型，难以全面分析多解的情况，解题低效。Hawgent皓骏动态数学软件功能强大、操作简便，具有数学化、视觉化、动态化呈现数学对象与思维的功能，是提效学生数学学习的神器。本文试图应用Hawgent皓骏动态数学软件，以较为典型的旋转求角问题为例，呈现旋转求角问题的教学片段及评析，以期提升几何开放题的教学有效性。

1 教学设计的基本思路

针对上述提及的不足，对“旋转求角问题”的教学进行思考。首先引导学生对例题进行审题，旋转问题要关注旋转中心、旋转角、旋转方向这三大基本要素，接着动态展示三角板的旋转过程，引导学生讨论旋转角与所求角之间的联系，将未知向已知转化，特别是要让学生抓住平行这个关键的前提条件，善于运用平行线间拐点模型。问题解决后，对解题思路与方法进行概括，同时结合平行线拐点模型复习回顾，这个环节注重发散学生思维，以灵活转化。最后以该例题的变式结尾，在变式拓展中体现变与不变的本质。

2 教学片段的实录评析

2.1 教学片段及实录

限于篇幅主要呈现解题阶段的教学片段。

典例：如图1，将一副三角板的直角重合放置，其中，∠A=30°，∠CDE=45°。若三角板ACB的位置保持不动，将三角板CDE绕点C旋转一周。在这一过程中，是否会存在△CDE其中一边与AB平行?如果存在，请你画出示意图，并直接写出∠ECB的大小；如果不存在，请说明理由。

（解题环节）师：我们选取顺时针为旋转方向讨论。在解决与旋转有关的问题时，我们需先确定旋转中心与旋转角，由题知，旋转中心为点C，旋转角为∠BCE，通过动态的展示（操作Hawgent皓骏动态数学积件），第一次平行发生在哪两条边之间呢？∠ECB如何求得？

生1：我发现第一次平行应该发生在AB//CD，这时候∠ECB，∠ACD都为旋转角，又因为AB//CD，所以∠ECB=∠ACD=∠BAC=30°。

师：非常好，你抓住了旋转角都相等这一个特点，还把平行当作解决问题的条件。

师：那么当△CDE继续旋转后，还能得到那些直线平行呢？让我们接着看。我们可以发现第二次平行是AB//CE，此时所求角为旋转角，∠BCE=120°是怎样得到的呢？

小圆：与第一次平行类似，∠BCE=∠ACB+∠ACE，因为AB//CE，所以∠ACE=∠A=30°，则∠BCE=∠ACB+∠ACE=90°+30°=120°。

师：哎，不错，看来这些都难不倒大家，继续旋转，我们发现，第三次平行时，有AB//DE，且∠CBE=165°，观察图像，∠ECB怎么求？

小静：可以发现∠ECB=∠BCA+∠ACE。

小方：（产生困惑）那∠ACE的度数该怎么得到呢？

师：我把几条主要的边用红线标出（如图1），大家看看有什么启发？

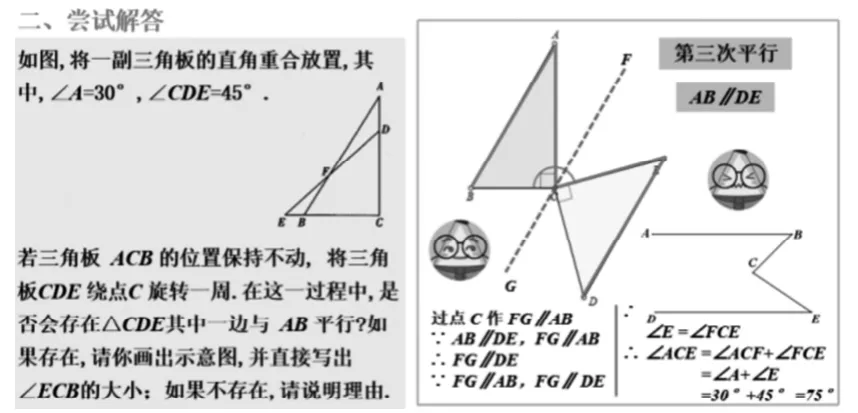
图1

小方：哦！可以过点C作平行线，然后再运用内错角相等！

师：是的，这就变成了我们之前常见的平行线间拐点问题。很容易发现这是我们熟悉的“铅笔型”。那你们能把证明过程写出来吗？

生2：没问题。过点C作FG//AB，∵AB//DE，FG//AB，∴FG//DE，∵FG//AB，FG//DE，∴∠A=∠ACF，∠E=∠FCE，∠ACE=∠ACF+∠FCE=75°，∴∠ECB=∠BCA+∠ACE=165°。

师：通过上述推导，再结合我们的动画观察（动态展示），相信同学们也能很轻易求出第四次与第五次平行，它们都是通过平行线的性质即可求得。

师：我们接着往下看，当出现第六次平行时（如图1，即AB//DE时，旋转角是哪个？此时要求解∠ECB是不是就有一些难度了呢？

生3：可以考虑用∠DCE减去∠DCB。

生4：我觉得也可以把它看作是平行线的拐点问题，可以过点C作AB的平行线。

师：不错，大家的方法都非常好。如果我们把几条边抽象出来，就可以把它看作是平行线间的拐点问题来求解，这也是我们所熟悉的“锄头型”。

小圆：我知道，∠BCE=∠BCG-∠GCE，过点C作平行线后，有FG//AB,FG//DE，所以∠ABC=∠BCG，∠E=∠GCE，代入求得∠BCE=∠BCG-∠GCE=∠ABC-∠E=15°。

师：非常好！

师：通过本节课学习，我们解决了这个“旋转求角”问题。大家有什么收获呢？

小方：我感受到要先弄清所求角与旋转角分别是谁，再通过图中角的关系求解。

师：有道理。其实我们可以把很多题目转化成学习过的几何模型来求解，只要把握住旋转中变与不变的量，善于联系已知模型，问题就会变得简单化。

师：最后老师准备了一个小问题供大家思考，同学们想一想，如果把题目中的“△CDE其中一边与AB平行”这个条件变式成“DE所在直线与AB垂直”，那么此时的旋转角大小是多少呢？请大家发挥自己的聪明才智，一起解决这个问题吧！

2.2 教学片段评析及反思

针对学生难以理解旋转中角度与角的关系如何变化的问题，本次教学结合Hawgent皓骏动态数学软件展示了“旋转求角问题”的解题过程，具有以下几个突出的亮点：

2.2.1 “拖”“动”结合，挖掘隐含条件

审题的关键在于引导学生弄清题意，学会分析题目中的已知和未知。首先，利用Hawgent皓骏动态软件，根据题意，以顺时针为旋转方向，拖动三角板CDE，可以直观看到旋转的三要素，即旋转中心、旋转角、旋转方向，其次，拖动三角板旋转一周，可确定旋转角的取值范围，明确旋转三要素是解决问题的切入口。教师结合动画演示，提问学生旋转角在变化过程中可由哪些角构成，师生互动解读隐含信息。

2.2.2 “数”“形”相依，明确旋转过程

解题环节建立在学生已有的知识经验上，首先，顺时针拖动三角板CDE，可直观看到旋转角的变化，当三角板发生平行时，要引导学生把平行当作条件，将所求角转化为已知角的和差关系，接着，在平行的前提下联系边角关系求解，引导学生思考如何将求角转化为已知几何模型，即将求角问题转化为平行线间的拐点问题。最后，让学生类比第三次平行来求解所有平行的情况。通过Hawgent皓骏动态数学技术软件的展示，结合题意呈现出三角板的旋转过程，主要突出旋转角的动态变化，“数”“形”相依。通过激发学生对旋转情况的讨论，不仅体现了学生的主体地位，同时达到了“授人以鱼的同时授人以渔与欲”的目的。

2.2.3 “动”“静”互用，发散解题思维

在解决这个旋转求角问题时，每一次平行都可以运用平行线的性质来求角度，并把其中几次平行抽象成已经学习过的拐点问题。在传统教学中，学生无法把握解题过程的动态变化，而运用动态技术，能促进学生对题目的理解，帮助提升学生的数学思维品质，培养学生的核心素养。除此之外，旋转求角还能将图形全等、相似、方程等结合起来。基于学生的学情和已有认知，在复习初中几何时，可以考虑以旋转这一类问题作为切入点，把其他的知识点有机结合起来系统地复习，开拓学生的多维度思考。

但是，用Hawgent皓骏动态数学软件提效几何开放题教学需要教师对Hawgent皓骏软件有一定的熟练度，同时要求教师在动态呈现过程中恰当地引导学生思考。