圆弧齿轮排肥器圆弧结构参数仿真试验及优化

顿国强，高志勇，郭艳玲*，刘宇轩，毛宁，纪文义

（1.东北林业大学机电工程学院，哈尔滨150040；2.东北林业大学工程技术学院，哈尔滨150040；3.东北农业大学工程学院，哈尔滨150030）

施肥是农业生产中的重要过程，不合理的施肥会影响农作物根系对养分的吸收，并导致土壤退化、肥力下降、板结等，不利于农业可持续发展[1]。排肥器是施肥作业中的重要机械部件，而机具作业性能对施肥的效果有着重要影响。目前，市面上主要使用的排肥器为外槽轮式排肥器，但由于排肥轮槽脊结构以及肥料颗粒尺寸不规则等因素的影响，外槽轮式排肥器在排肥过程中经常出现肥量不均匀、断条等现象[2]。

有关外槽轮式排肥器的研究主要包括结构参数与工作参数对排肥性能的影响等方面，如：顿国强等[3]采用工程离散元法（engineering discrete element method,EDEM），分析了外槽轮式排肥器排肥舌倒角机构参数对排肥均匀性的影响；杨洲等[4]利用EDEM 和三维打印成型技术分析了外槽轮式排肥器槽轮凹槽半径、螺旋升角和转速等参数对排肥量的影响；张涛等[5]通过模拟外槽轮式排肥器排肥过程，得出外槽轮不同工作长度对排肥量的影响；汪博涛等[6]分析了外槽轮工作长度、排肥轴转速、排肥舌开口角度对排肥均匀性的影响，并根据结果分析进行了参数优化；吕昊[7]利用自主研发的离散元仿真软件对外槽轮式排肥器的肥料颗粒运动状态及排肥特性进行了仿真分析。目前，对于排肥器排肥性能的研究，大多集中在对外槽轮式排肥器结构参数的优化上，无法解决排肥轮槽脊结构造成流量均匀性较差的问题。因此，设计新型排肥器对提升排肥流量均匀性具有十分重要的意义。

基于此，本研究设计了提高排肥流量均匀性的圆弧齿轮排肥器。首先，通过对排肥器结构设计与理论分析，确定了影响圆弧齿轮排肥器排肥量的因素；其次，设计了二因素五水平的二次正交旋转试验，并应用EDEM仿真技术对不同参数下的圆弧齿轮排肥器的排肥状况进行分析；最后，制造出最优结构参数的圆弧齿轮排肥器，并进行了台架试验。旨在为优化圆弧齿轮排肥器的圆弧结构参数和提高排肥均匀性提供参考。

1 离散元法理论模型

离散元法能够根据颗粒间的运动力以及颗粒之间的碰撞，将颗粒间的力进行传递来分析模型之间的受力情况。离散元法描述碰撞的过程就是接触的产生和发生作用的过程。排肥器工作时，多个肥料颗粒相互摩擦碰撞，适合离散元法中软球颗粒分析理论，因此，本研究采用软颗粒接触模型[8]；考虑到普通化肥之间没用黏结力，故采用赫兹（无滑动）接触模型[9]。

离散元法通过在颗粒i和j（或者接触壁）间设定弹簧、阻尼器、滑动器与耦合器的方式来模拟软颗粒之间的接触形式[10-12]，如图1所示。

2 外槽轮式排肥器和圆弧齿轮排肥器对比分析

2.1 排肥器结构对比

如图2A 所示，外槽轮式排肥器主要由外壳、排肥外槽轮和排肥舌等组成，且外槽轮的槽脊结构容易造成排肥间断。如图2B所示，圆弧齿轮排肥器主要由壳体，圆弧排肥齿轮，主、从动齿轮轴和驱动六方轴孔等组成。圆弧齿轮排肥器通过变频器调节圆弧排肥齿轮的转速来控制排肥量，电机通过驱动六方轴以驱动主动齿轮轴转动，两直齿渐开线圆柱齿轮轴通过转动传递动力，直齿渐开线圆柱齿轮轴与圆弧排肥齿轮间通过螺钉连接传动。

2.2 排肥器排肥效果对比

本研究所设计的圆弧齿轮排肥器相比于外槽轮式排肥器的突出优点是能够提高排肥流量的均匀性。如图3 所示，利用EDEM 软件模拟2 种排肥器的排肥过程，分别取一个工作循环进行对比分析。

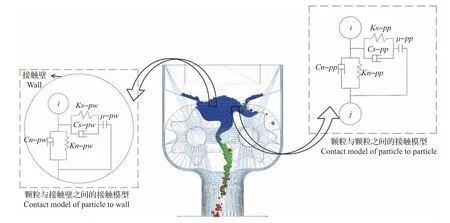
图1 软球模型对颗粒间（或颗粒-接触壁间）接触力的简化处理Fig.1 Simplifying treatment of contact forces of particle to particle(or particle to wall)by soft-sphere model

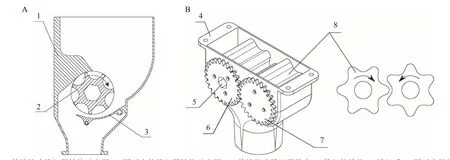
图2 2种排肥器结构对比Fig.2 Comparison of two fertilizer apparatuses’ structures

从图3A 中可看出：当外槽轮式排肥器的槽结构刚到排肥舌时，前一槽里的肥料已经完全掉落，造成“断条”现象；而当槽结构全部越过排肥舌时，槽里的肥料堆积掉落；如此循环往复，造成排肥不均匀。从图3B中可看出：肥料经圆弧排肥齿轮间隙实现排肥，圆弧排肥齿轮间隙大小稳定，且圆弧齿轮的齿槽连续交替运动，提高了排肥流量的均匀性，避免了普通排肥器的堵塞和间歇性排肥问题。

3 圆弧齿轮排肥器结构理论分析

分析排肥器关键结构参数，排肥器排出肥料的总质量计算公式如下：

式中：m表示排出肥料的质量，g；ρb表示肥料的堆积密度，g/mm3；V表示排出肥料的体积，mm3。

由式（1）知，排肥器排出肥料的质量m为肥料的堆积密度ρb和排出肥料的体积V的乘积，而肥料的堆积密度ρb为肥料的固有属性。因此，若要改变排出肥料的质量m，只有通过改变排出肥料的体积V来实现。

图3 2种排肥器排肥效果对比Fig.3 Comparison of two fertilizer apparatuses’ discharging effects

如图4所示，排出肥料的体积V计算公式如下：

式中：l表示两圆弧排肥齿轮之间的最小槽长，mm；l′表示圆弧排肥齿轮工作槽段长度，mm；L表示圆弧排肥齿轮转动1周的长度，mm；ω表示圆弧排肥齿轮转动的速度，r/min；t表示圆弧排肥齿轮转动时间，s。

图4 排肥器设计参数Fig.4 Design parameters of fertilizer apparatus

其中，两圆弧排肥齿轮之间的最小槽长l为：

式中：r1为圆弧排肥齿轮的轮槽圆弧半径，mm；r2为圆弧排肥齿轮的轮脊圆弧半径，mm。

截取部分图4 所示圆弧齿轮排肥器，放大后如图5所示。圆弧排肥齿轮实际上是由半径为r1的圆弧GB、半径为r2的圆弧CF及其两段公切线BC与FI的圆周阵列所组成，其中BC与FI等长。连接AB、CD、AD、AO、DO，同时，AD交公切线BC于E，令∠EAB为δ，∠DAO为θ。令AE=c1，DE=c2，AD=c，BC=a；结合图4可知，DO=R，AO=l－R。

结合圆弧齿轮排肥器设计与图5基本参数计算排肥量参数的公式如下。

圆弧排肥齿轮转动1周的长度L为：

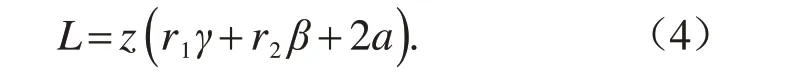
式中：z为圆弧排肥齿轮齿数；β为圆弧排肥齿轮轮脊圆弧圆心角，rad；γ为圆弧排肥齿轮轮槽圆弧圆心角，rad。其中，圆弧排肥齿轮齿数z为：

式中：α为轮脊圆弧圆心与轮槽圆弧圆心夹角，rad。

由几何关系知，圆弧排肥齿轮轮脊圆弧圆心角β和圆弧排肥齿轮轮槽圆弧圆心角γ分别为：

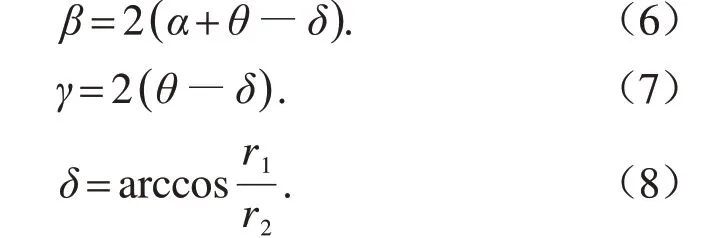
对于不同的施肥对象，由式（2）可知，影响圆弧齿轮排肥器排肥性能的圆弧结构参数主要有两圆弧排肥齿轮之间的最小槽长l、圆弧排肥齿轮工作槽段长度l′、圆弧排肥齿轮转动1 周的长度L。由式（4）～（14）可知，圆弧排肥齿轮转动1周的长度L由齿数z、两圆弧排肥齿轮中心距l′′、等效半径r、圆弧排肥齿轮的轮槽圆弧半径r1和圆弧排肥齿轮的轮脊圆弧半径r2共同决定；而由式（3）可知，两圆弧排肥齿轮之间的最小槽长l与圆弧排肥齿轮的轮槽圆弧半径r1、圆弧排肥齿轮的轮脊圆弧半径r2有关。而圆弧排肥齿轮工作槽段长度l′、两圆弧排肥齿轮中心距l′′是制造圆弧齿轮排肥器的固有参数。

综上分析，为探索圆弧结构参数对圆弧齿轮排肥器排肥性能的影响，考虑到实际情况，选取r=34 mm，l′=50 mm，l′′=70 mm 作为本研究的不变因素[12]，选取圆弧排肥齿轮的轮槽圆弧半径r1和两圆弧排肥齿轮之间的最小槽长l作为影响因素，如图6所示。

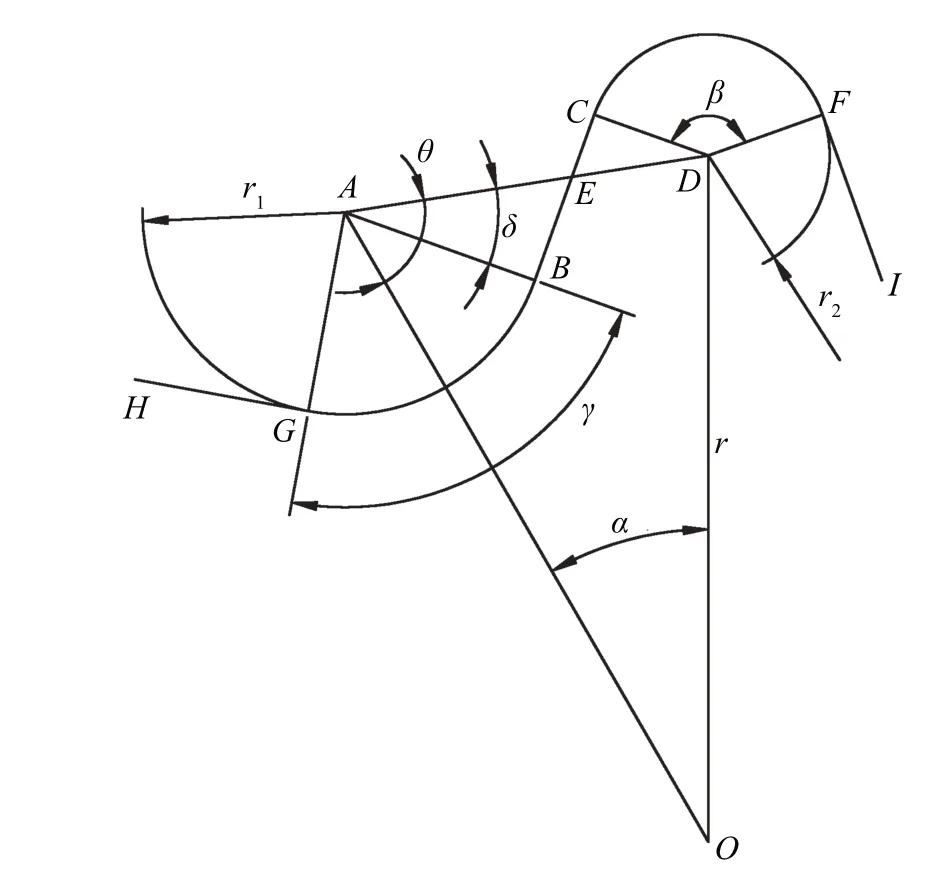
图5 参数计算图解Fig.5 Diagram of parameter calculation

4 基于离散元法的仿真试验

离散元法作为有效的颗粒体运动的分析方法，已经在工业、农业等领域被广泛应用[13-14]。通过前述理论分析，本研究选取圆弧排肥齿轮的轮槽圆弧半径r1和两圆弧排肥齿轮之间的最小槽长l这2 个因素进行仿真试验。试验采用单因素分析和响应曲面设计。

4.1 仿真试验设计

为探究r1和l这2 个影响因素对排肥性能的影响，设计相应的试验方案[15]。在研究圆弧排肥齿轮的轮槽圆弧半径r1对排肥性能的影响时，设计转速为40 r/min，以圆弧排肥齿轮的轮槽圆弧半径r1为试验因素，根据实际要求，r1选7、8、9、10、11 mm 共5 组试验，每组试验设置3 个重复；在研究两圆弧排肥齿轮之间的最小槽长l对排肥性能的影响时，设计转速为40 r/min，以圆弧排肥齿轮之间的最小槽长l为试验因素，根据实际要求，l选3、4、5、6、7 mm共5 组试验，每组试验设置3 个重复。试验在排肥器出肥口处设置监测网格（a），通过监测网格内排肥量稳定性变异系数σ来反映排肥流量的均匀性；在肥料收集器底部设置排肥量监测网格（b），通过监测网格内单位时间排肥量的决定系数R2来反映排肥流量的均匀性。

4.2 肥料颗粒模型的建立

选择山东兖矿鲁南化肥厂生产的尿素作为离散元建模的试验材料，从化肥中随机抽取100 粒尿素颗粒，使用世达牌91512数显式游标卡尺[世达工具（上海）有限公司]测得尿素颗粒长、宽、高的平均值分别为2.52、2.49、2.61 mm，使用UTP-313型电子天平（上海花潮电器有限公司）测得尿素单粒平均质量为0.011 g。经过统计计算，单粒尿素的等效直径为2.54 mm，密度为1 283 g/mm3。在EDEM 颗粒工厂中，设置颗粒平均半径为1.27 mm，大小服从μ=1.27，σ2=0.29的正态分布。参数设置如表1所示。

4.3 接触参数的设置

本研究采用赫兹（无滑动）模型作为尿素颗粒与颗粒、圆弧齿轮排肥器（材料为聚乳酸）之间的接触模型。参考文献[16]，EDEM 上的具体参数设置如表2所示。

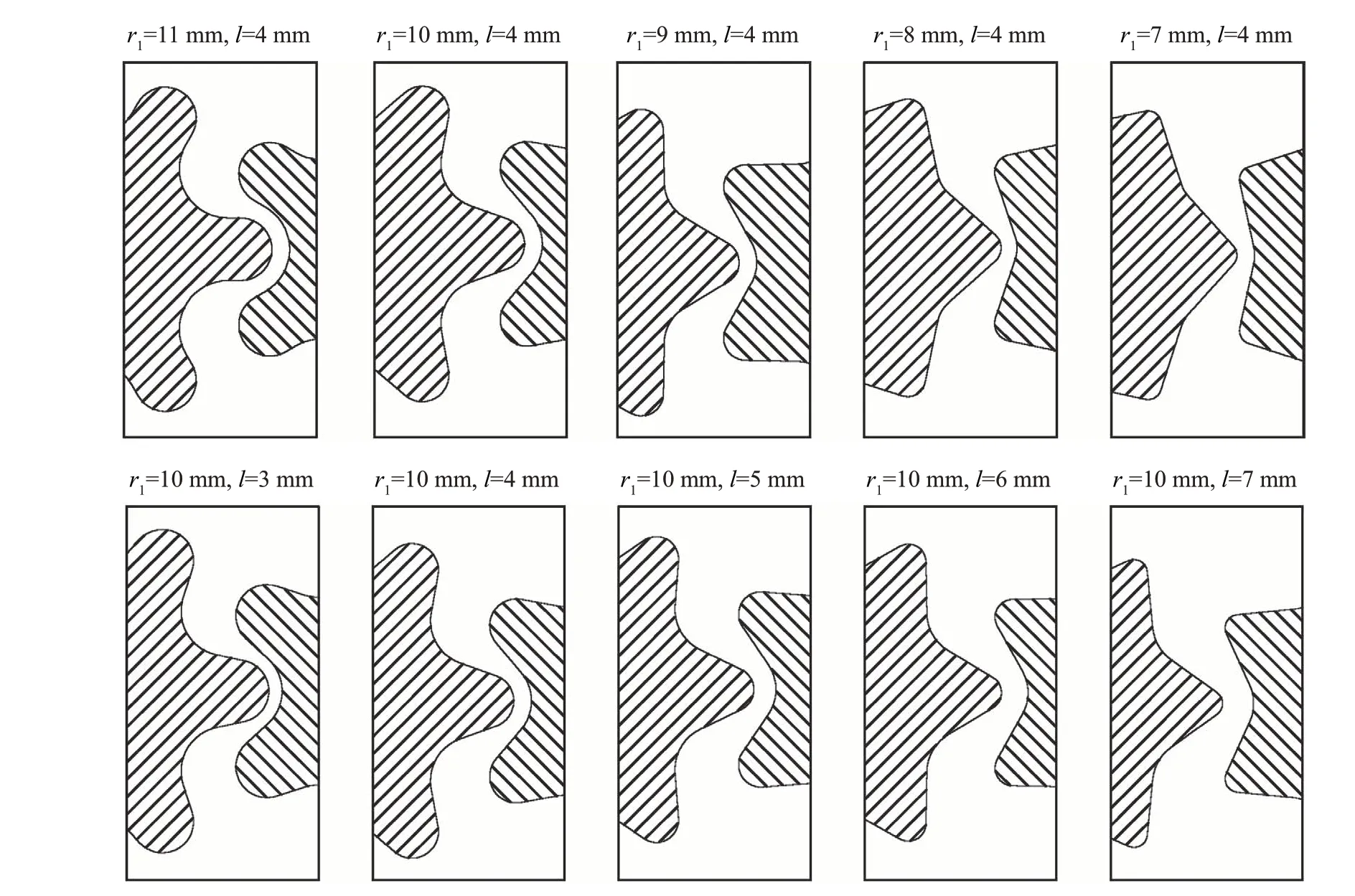
图6 r1和l对圆弧排肥齿轮形状的影响Fig.6 Influence of r1 and l on the circular arc discharging fertilizer gear’s shape

表1 EDEM中颗粒参数设置Table 1 Setting of particle parameters in EDEM

4.4 几何模型的建立和导入

使用Solidworks 2016进行圆弧齿轮排肥器的设计和三维模型建立，除去不必要的、非接触的结构设计，并另存为.step格式文件。在EDEM中导入.step文件，并进行模型零件参数设置。为排肥轮设置转速，同时设置颗粒工厂（particle factory）参数，其中生产颗粒总数（total number）设置为3 000，每秒生产颗粒数目（target number per second）为3×104，仿真模型如图7所示。

表2 EDEM中变量参数设置Table 2 Setting of variable parameters in EDEM

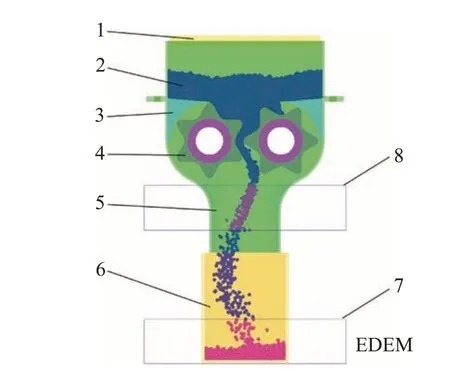
图7 仿真几何模型Fig.7 Model of simulation geometry

4.5 仿真计算设置

设置瑞利时间步长（Rayleigh time step）为5×10－6s，仿真总时长（total time）为2 s，数据记录时间间隔（target save interval）为0.01 s，设定网格尺寸（simulator cell size）为3Rmin。

5 基于响应曲面的试验设计

响应曲面法（response surface methodology,RSM）是运用数学和统计方法，对多变量问题进行数学建模分析，从而获取最优工艺条件或者参数的方法[17]。以监测网格（a）内排肥量稳定性变异系数σ和监测网格（b）内单位时间排肥量的决定系数R2为试验指标，进行响应曲面试验。

5.1 排肥均匀性的评价指标

据4.1节的介绍，试验在排肥器出肥口处设置监测网格（a），在EDEM的后处理模块设置输出折线图（line）的时间范围（time range）为0.3～2.0 s，Y轴的属性（primary attribute）设置为质量（mass,total），如图8所示。

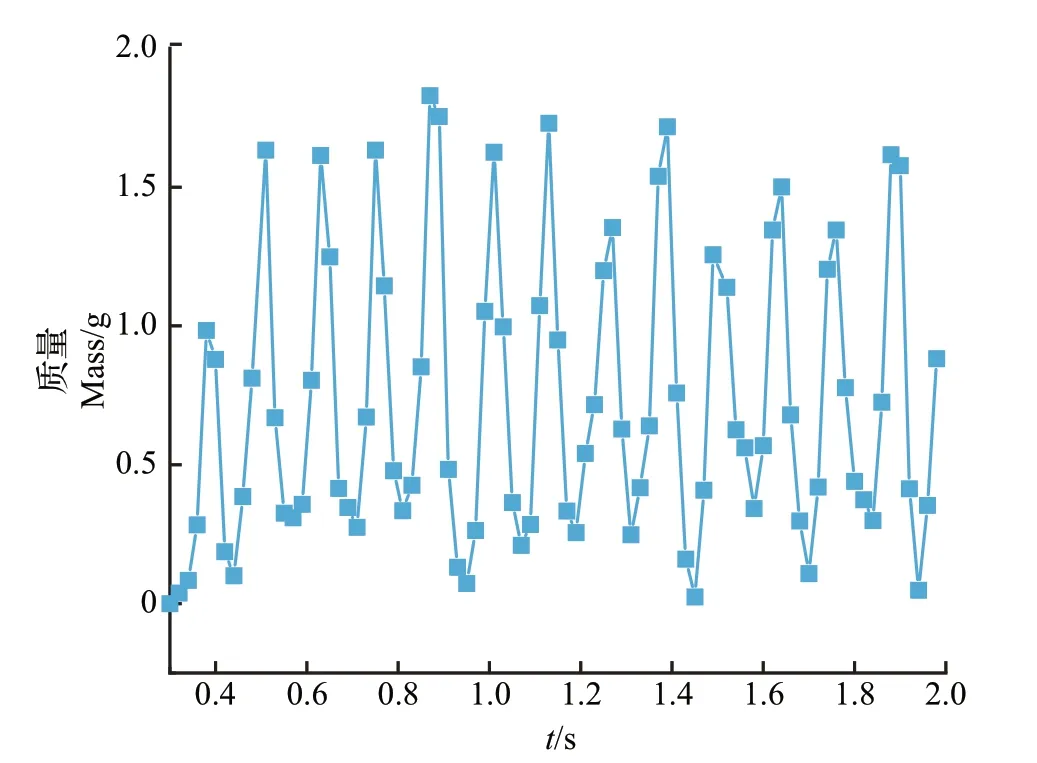
图8 单次试验监测网格（a）内肥料颗粒质量变化Fig.8 Mass change of fertilizer particle from monitoring grid(a)in single experiment

式中：σ为0.3～2.0 s 时间内通过监测网格（a）的肥料颗粒质量的变异系数。

试验在肥料收集器底部设置排肥量监测网格（b），在EDEM的后处理模块设置输出折线图（line）的时间范围（time range）为0.3～2.0 s，Y轴的属性（primary attribute）设置为质量（mass, total），如图9所示。

每次试验设置圆弧排肥齿轮的转速为20、40、60、80、100 r/min，分别进行3次试验，以不同转速时的监测网格（b）内单位时间排肥量的决定系数R2来反映排肥流量的均匀性，如式（18）～（19）所示。

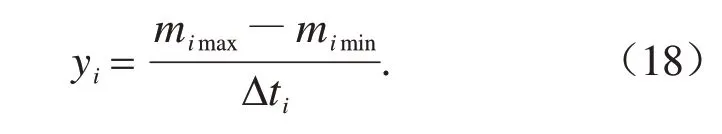
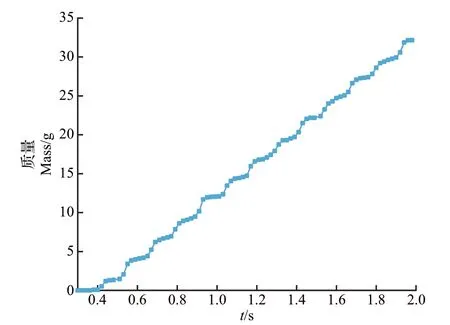
图9 单次试验监测网格（b）内肥料堆积质量变化Fig.9 Mass change of fertilizer accumulation from monitoring grid(b)in single experiment

式中：i=1, 2, 3, 4, 5，分别表示在转速为20、40、60、80、100 r/min 时的试验；yi为第i次试验时单位时间排肥量，g/s；mimax为第i次试验时0.3～2.0 s 内肥料最大堆积量，g；mimin为第i次试验时0.3～2.0 s 内肥料最小堆积量，g；Δti为第i次试验的仿真时间差，s，此处Δti=1.7 s。

式中：R2为决定系数；SSR 为数据的回归平方和（sum of squares for regression）；SST 为数据的总离差平方和（sum of squares for total）。

5.2 试验方法及结果

为探索圆弧结构参数对圆弧齿轮排肥器排肥性能的影响，选取圆弧排肥齿轮的轮槽圆弧半径r1和两圆弧排肥齿轮之间的最小槽长l作为影响因素，采用二因素五水平的二次旋转正交试验设计，用Design-Expert 8.0 分析软件进行数据处理[18]，优化选出排肥量最均匀的圆弧排肥齿轮结构参数，如表3～4所示。

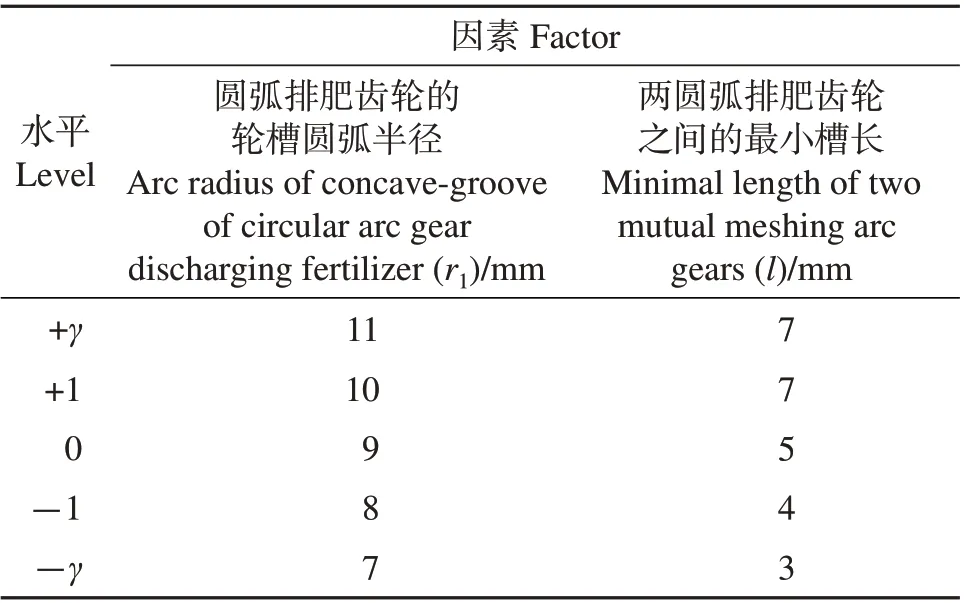
表3 试验因素与水平Table 3 Experimental factors and levels

表4 二次正交旋转试验方案及结果Table 4 Experimental schemes and results of quadratic orthogonal rotary

6 试验结果与分析

6.1 监测网格（a）内排肥量稳定性变异系数的方差分析

根据表4 的试验数据，应用Design-Expert 8.0软件得出监测网格（a）内排肥量稳定性变异系数σ的方差分析结果（表5）。由此得出影响监测网格（a）内排肥量稳定性变异系数σ的2个因子与性能指标的关系：

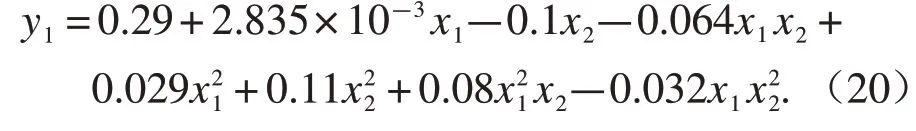
由表5的方差分析结果可知，因子x2极显著，因子x1x2、x22、x21x2在水平α=0.05 时显著，其他因子不显著。

6.2 监测网格（b）内单位时间排肥量决定系数的方差分析

根据表4 的试验数据，应用Design-Expert 8.0软件得出监测网格（b）内单位时间排肥量的决定系数R2的方差分析结果（表6）。由此得出监测网格（b）内单位时间排肥量决定系数R2的2 个因子与性能指标的关系：

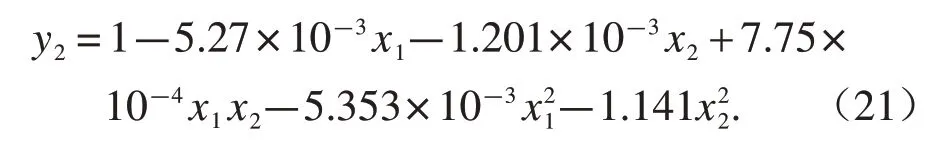
由表6的方差分析结果可知，因子x1极显著，因子x21在水平α=0.05时显著，其他因子不显著。

表5 各因子对监测网格（a）内排肥量稳定性变异系数影响的方差分析Table 5 Variance analysis of the influence of each factor on the stability coefficient of variation of discharging fertilizer in monitoring grid(a)

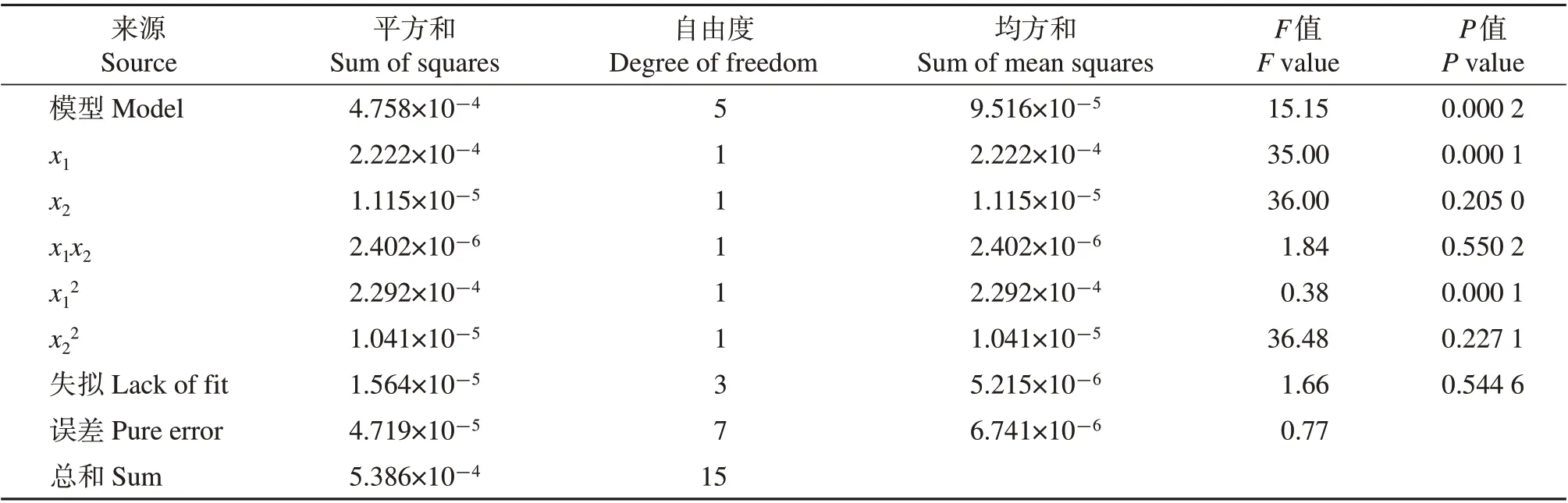
表6 各因子对监测网格（b）内单位时间排肥量的决定系数影响的方差分析Table 6 Variance analysis of the influence of each factor on the coefficient of determination of discharging fertilizer per unit time in monitoring grid(b)

6.3 监测网格（a）内颗粒肥料质量变化变异系数的响应曲面分析

由图10 可知：监测网格（a）内排肥量稳定性变异系数最小值为0.200，响应曲面沿圆弧排肥齿轮的轮槽圆弧半径方向变化较缓慢，且随着r1数值的增大，变异系数呈现先增大后减小的趋势；响应曲面沿两圆弧排肥齿轮之间的最小槽长方向变化较明显，随着l数值的增大，变异系数呈现先减小后增大的趋势。由实际工作状态和图6 易知：当l增大时，两圆弧排肥齿轮之间的间隙增大，当轮槽和轮脊交替时，肥料滑落，造成排肥不均匀；当l减小时，肥料不易下落，排肥也不均匀。

6.4 监测网格（b）内单位时间排肥量决定系数的响应曲面分析

由图11 可知：监测网格（b）内单位时间排肥量的决定系数最大值为0.995，响应曲面沿圆弧排肥齿轮的轮槽圆弧半径方向变化较明显，且随着r1数值的增大，决定系数呈现先增大后减小的趋势；响应曲面沿两圆弧排肥齿轮之间的最小槽长方向变化较缓慢，随着l数值的增大，决定系数呈现先增大后减小的趋势。

6.5 最佳参数验证

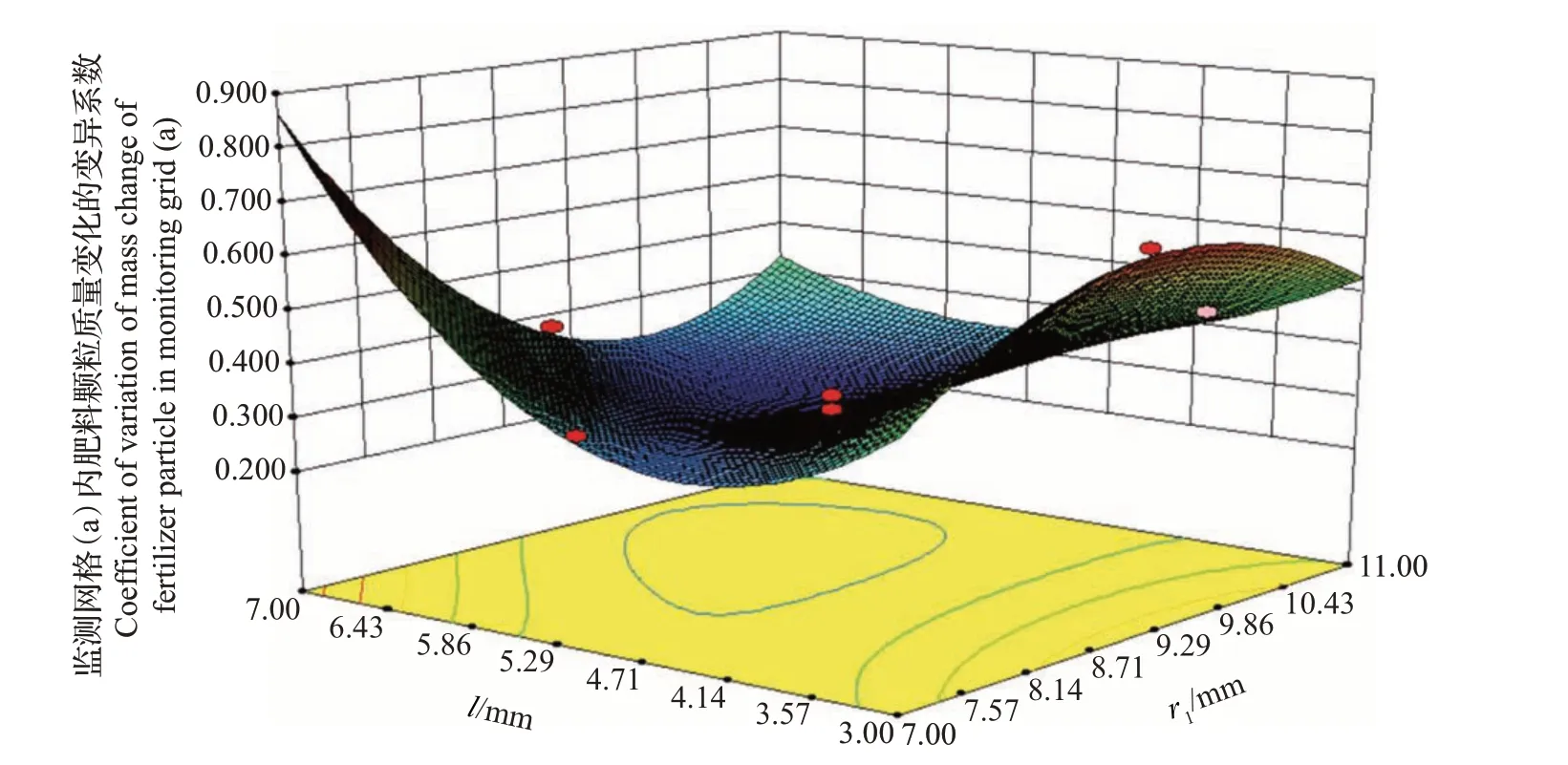
图10 最小槽长l与轮槽圆弧半径r1对变异系数的响应曲面图Fig.10 Response surface map of the minimal length of two mutual meshing arc gears l and the arc radius of concave-groove r1 to coefficient of variation

图11 最小槽长l与轮槽圆弧半径r1对决定系数的响应曲面图Fig.11 Response surface map of the minimal length of two mutual meshing arc gears l and the arc radius of concave-groove r1 to coefficient of determination

利用Design-Expert 8.0软件对优化参数进行分析，监测网格（a）内排肥量稳定性变异系数σ取最小值，监测网格（b）内单位时间排肥量的决定系数R2取最大值，得出最优的参数组合：圆弧排肥齿轮的轮槽圆弧半径为8.54 mm，两圆弧排肥齿轮之间的最小槽长为5.22 mm，此时，变异系数为0.28，决定系数为0.997 2。

为验证最优参数的作业效果，在东北林业大学林业与木工机械工程技术中心对圆弧齿轮排肥器进行台架试验，试验装置如图12所示。

试验装置由试验台架、步进电机、圆弧齿轮排肥器、肥料箱、传输带等组成，利用该试验装置进行排肥器排肥效果验证。以尿素为试验材料，设置排肥轮转速为40 r/min，试验时间为10 s，并设置5 次重复，进行验证试验。由试验结果可知，排肥量稳定性变异系数为0.27，单位时间排肥量的决定系数为0.998 0。与理论值变异系数0.28、决定系数0.997 2相比，相对误差分别为－3.57%和0.08%。相对误差较小，表明试验结果可靠。由此说明，此参数下的圆弧齿轮排肥器排肥更加均匀，符合田间施肥要求。

7 结论

图12 3D打印模型及试验装置Fig.12 Three-dimension printing model and experimental equipment

1）设计了圆弧齿轮排肥器，对圆弧排肥齿轮的结构参数进行了理论分析，探索了圆弧结构参数对圆弧齿轮排肥器排肥均匀性的影响，建立了圆弧排肥齿轮的轮槽圆弧半径r1和两圆弧排肥齿轮之间的最小槽长l与排肥均匀性数学指标之间的关系。

2）应用EDEM 仿真软件进行了圆弧齿轮排肥器排肥过程的仿真，并进行了二因素五水平的二次旋转正交试验。仿真试验结果表明：圆弧排肥齿轮的轮槽圆弧半径对单位时间排肥量的决定系数影响显著，两圆弧排肥齿轮之间的最小槽长对排肥量稳定性变异系数影响显著，得出的最优结构参数为圆弧排肥齿轮的轮槽圆弧半径8.54 mm，两圆弧排肥齿轮之间的最小槽长5.22 mm，此时，变异系数为0.28，决定系数为0.997 2。

3）根据最优参数制造圆弧齿轮排肥器，并进行台架试验，其排肥量稳定性变异系数为0.27，单位时间排肥量的决定系数为0.998 0，与理论值变异系数0.28、决定系数0.997 2 相比，相对误差分别为－3.57%和0.08%。相对误差较小，表明试验结果可靠。说明利用离散元法来模拟排肥器工作过程是可靠的。