基于文化混洗蛙跳算法求解连续空间优化问题

张 强, 朱刘涛, 王 颖

(东北石油大学 计算机与信息技术学院, 黑龙江 大庆 163318)

混洗蛙跳算法(shuffled frog leaping algorithm, SFLA)[1]是一种具有粒子群优化算法全局搜索和模因算法局部搜索的元启发式智能优化算法, 具有收敛较快、 参数调整少、 搜索能力强等优势, 已广泛应用在函数优化[2-3]、 车间调度[4-6]、 故障诊断[7-8]、 聚类问题[9-10]和图像处理[11-12]等领域. 但该算法也存在一些不足： 1) 混洗蛙跳算法按适应值降序的方式分配到子群内, 导致最后一个子群内个体的适应值整体偏低, 从而影响整个蛙群的寻优性能； 2) 每个子群内更新最差青蛙, 并根据子群内的最优青蛙调整位置, 易导致最差青蛙具有趋同性, 使青蛙种群多样性降低, 对于多模优化问题混洗蛙跳算法易陷入局部最优； 3) 混洗蛙跳算法未充分利用整个蛙群中其他个体的迭代寻优信息, 导致子群易被限制在较小的寻优空间. 文献[13-15]提出了一种文化算法理论, 该算法是由信念空间和群体空间构成的双层进化结构. 群体空间通过接受函数将优秀青蛙的经验选择性地传递到信念空间, 而信念空间再通过影响函数将进化过程中的优秀经验反馈到群体空间, 以指导个体的进化, 通过两个空间的相互影响准确反映进化过程, 进而提高寻优效率和速率. 本文通过在基本混洗蛙跳算法原理的基础上引入文化算法的理念, 提出一种文化混洗蛙跳算法(cultural shuffled frog leaping algorithm, CSFLA), 改进了群体空间和信念空间内个体的进化方式, 设计了相应的接受函数实现个体优秀经验及进化信息的有效传递, 并通过影响函数将信念空间的进化信息反馈到群体空间, 以进一步指导青蛙个体在优化问题空间进行有效寻优.

1 基本混洗蛙跳算法

基本混洗蛙跳算法的思想是将整个青蛙群体分为不同的子群体, 每个子群体的最差个体先向子群内最优个体学习产生新个体, 如果新个体优于最差个体则替换; 否则再向种群最优个体学习产生新个体, 如果新个体优于最差个体则替换; 否则随机产生一个个体. 当子群进化到指定次数后就重新划分子群进行寻优, 直至满足所设置的结束条件.

1.1 种群初始化

混洗蛙跳算法将每只青蛙都视为优化问题的解, 设青蛙种群规模为P(P=mn, 其中m为子群个数,n为子群内青蛙个数), 最大进化代数为T, 子群迭代次数为t.

1.2 子群划分原理

先计算每个青蛙的适应度f(X), 再按降序排序. 设蛙群中适应值最好的青蛙为Pg, 用X(j)k表示第k个分组内的第j个青蛙,j=1,2,…,n,k=1,2,…,m. 按

Gk={X(j)k,f(j)k|X(j)k=X(k+m(j-1)),f(j)k=f(k+m(j-1))}

(1)

将青蛙种群分为m个子群, 每个子群均包含n个青蛙. 图1为蛙跳算法分组示意图.

1.3 子群内青蛙进化

设每个子群内最优解为Xb, 最差解为Xw, 整个种群当前最优解为Xg, 利用下式对每个子群的Xw进行更新：

(2)

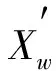
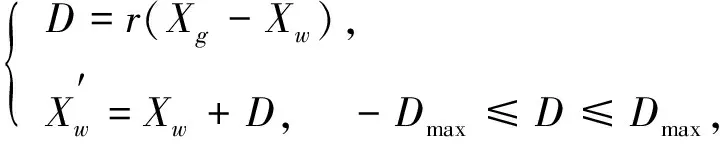
(3)

图1 蛙跳算法分组示意图Fig.1 Schematic diagram of frog leaping algorithm grouping

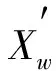
当每个子群分别迭代指定次数时, 如果达到群体进化最大进化代数T或满足寻优精度则输出结果, 否则将所有青蛙个体整合完成青蛙种群的信息共享, 继续进行子群划分、 子群个体进化, 直至满足算法终止条件.

2 文化混洗蛙跳算法原理

文化混洗蛙跳算法的基本框架由种群空间和信念空间构成. 种群空间包含优化问题的候选解, 主要由采用蛙跳算法的进化方式进行寻优; 信念空间主要用于保存进化过程中的优秀经验, 采用螺旋更新的方式在最优解附近寻找更优解, 进而加速寻优性能. 信念空间通过接受函数从群体空间获得优秀个体； 通过信念空间的不断进化后, 再通过影响函数将优秀个体的经验反馈给群体空间, 进而指导群体空间的个体进化.

2.1 群体空间进化方式

文化混洗蛙跳算法群体空间进化方式仍采用经典混洗蛙跳算法的更新方式, 即只更新每个分组内的最差个体. 但原算法最差个体是先向组内最优个体学习, 未改善则再向当代整个蛙群最优个体学习, 这种学习方式较单一, 未充分考虑个体经验和全局经验的相互作用关系, 易导致算法陷入局部最优. 基于此, 本文提出一种改进方法, 将向种群最优个体学习的方式改进成向组内最优个体、 种群最优个体和信念空间个体(信念空间通过影响函数提供)同时学习, 实现公式为

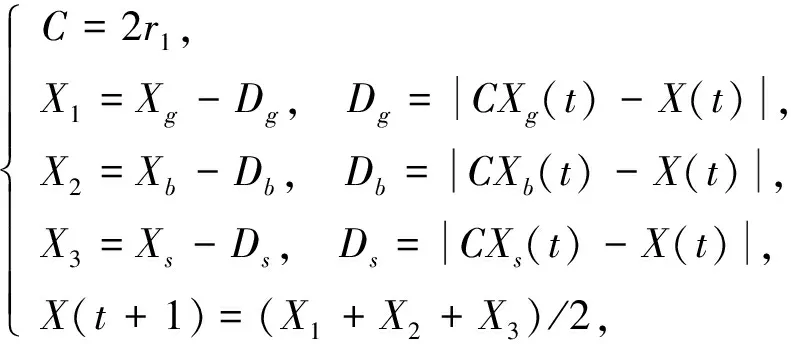
(4)

其中:Xg(t)为种群最优个体；Xb(t)为组内最优个体；Xs(t)为信念空间的个体；t表示当前迭代次数；X(t+1)为第(t+1)代青蛙的位置；r1在[0,1]内随机取值.

2.2 信念空间进化方式

信念空间内的个体来自于群体空间的较优个体. 研究表明, 优秀个体附近更易找到更优个体, 所以可对信念空间内的个体进行寻优. 为模拟个体进行周围寻优的进化方式, 本文个体位置更新采用螺旋方式, 同时为降低信念空间个体聚集到局部最优解的几率, 需个体以一定概率进行随机游走. 如果通过螺旋更新或随机游走方式获得的个体优于原个体则替换, 否则不进行任何操作. 个体跳跃步长计算公式为

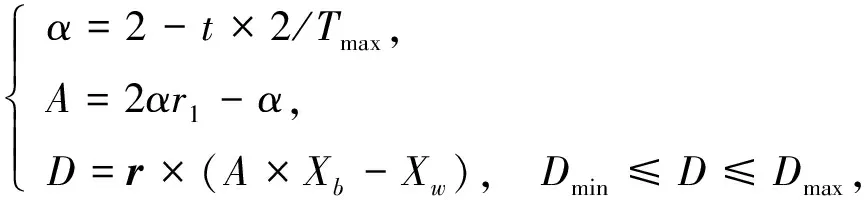
(5)

其中:Xb为信念空间内最优个体;Xw为组内最优个体;t表示当前迭代次数;Tmax为最大迭代次数；r,r1在[0,1]内随机取值.

本文将扰动系数A作为概率阈值, 在优化过程中,A的变化范围随着α的减小而减小; 当|A|≤1时, 使用螺旋进化方式更新位置, 能加快族群内的青蛙向最优位置靠拢; 当|A|>1时, 采用个体随机游走方式完成对猎物的捕食.

1) 个体螺旋进化寻优. 首先计算信念空间内最优个体与最差个体之间的距离, 然后在最优个体与最差个体间创建螺旋运动轨迹, 促使青蛙种群在迭代中快速聚集在某一区域, 以加快算法后期的收敛速度, 其更新公式为

(6)

其中:l为[-1,1]内的随机概率；Xb表示信念空间内最优个体.

2) 个体随机游走. 以信念空间内最优个体为参照, 适当扩大蛙群的搜索范围, 并使空间内的青蛙由原位置不断向最优解位置移动, 其更新公式为

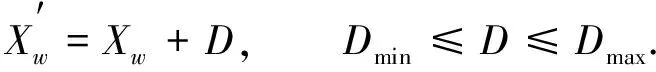
(7)

2.3 接受函数

接受函数的作用是从群体空间将优秀个体输送到信念空间. 本文算法设信念空间的个体数量为子群个数的2倍(2m个), 在算法迭代初期子群内的个体分布相对分散, 所以每个子群将最好的两个个体输送到信念空间. 但算法到迭代后期, 每个子群的个体位置相对集中, 故算法通过下式计算每个子群的方差：

(8)

2.4 影响函数

影响函数的作用是将信念空间的优秀经验传递给群体空间, 用于指导个体进行寻优, 其主要思想是通过引入较优个体引领整个子群内个体的进化. 首先, 在信念空间选择适应度最好的m个个体(m为子群个数)； 其次, 为改进后续子群整体适应度值偏低的情形, 将算法按适应度升序把m个个体分配给文化蛙跳算法的m个子群, 即将适应度最好的个体分配给最后一个子群, 适应度第二好的个体分配给倒数第二个子群, 以此类推.

3 仿真实验

本文选用如表1所示的12个常用基准测试函数(包括单峰问题和多峰问题)进行仿真实验.

表1 12个典型优化函数

Table 1 Twelve typical optimization functions

将文化混洗蛙跳算法(CSFLA), 与混洗蛙跳算法的4种改进算法(MSFLA[16],MSFLA1[17],ISFLA[18],MSFLA2[19])以及近几年提出的8种智能算法(鲸鱼优化算法(WOA)[20]、 灰狼算法(GWO)[21]、 飞蛾扑火算法(MFO)[22]、 布谷鸟算法(CSA)[23]、 蝙蝠算法(BAT)[24]、 多元宇宙算法(MVO)[25]、 果蝇算法(FFOA)[26]、 乌贼算法(CFA)[27])进行对比实验. 实验环境为: Intel(R)Core(TM)i7 8750H CPU双核处理器(2.20 GHz, 2.21 GHz), 16 GB内存, Microsoft Windows 10 Professional操作系统, 采用MATLAB R2014a进行编码并实现. 对每个测试函数, 本文算法及4种蛙跳改进算法均采用相同的参数设置, 其他8种算法参数均按原文献的设置方式. 设最大迭代次数为100, 种群数为40, 子群数为5, 每种算法分别计算20次取平均值. 每种算法分别对12个函数的100维进行优化对比, 性能对比结果如图2所示.

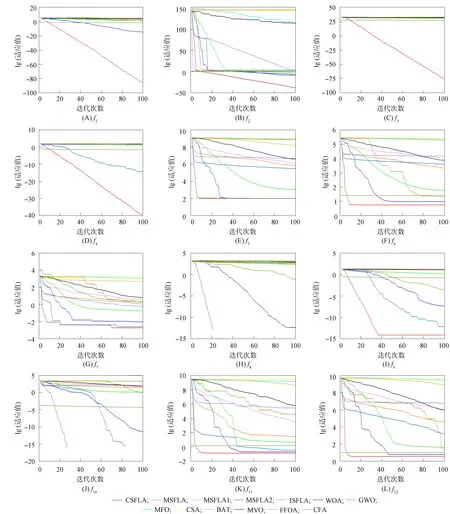
图2 不同算法对不同测试函数的迭代曲线对比Fig.2 Comparison of iterative curves of different algorithms for different test functions

由图2可见： CSFLA的寻优速度和寻优精度均优于其他对比算法； WOA的寻优性能相对较好, 但并非对12个优化函数都优于其他算法, 其他算法在一些函数也有一定的优势; 从单峰函数f1～f4的迭代曲线可见, CSFLA相对于其他算法, 能快速收敛到最优解. 多峰多极值函数局部极值的个数随维数的增加而呈指数级增长, 但由多峰多极值函数f8～f10的优化结果可见, CSFLA均求解到了最优值0, 即使在500维函数测试也能求解到最优值, 函数f6,f7,f9,f11,f12的优化结果优于其他对比算法, 且从迭代曲线可见, 算法可在40次迭代内即能获得较好的结果, 这也表明由于信念空间个体优秀经验的反馈, 加速了算法寻优效率, 提高了寻优性能.

为验证本文算法对高维优化问题的求解能力, 选取函数f3～f12作为测试函数, 优化问题维数设为500, 其他算法运行参数不变. 选取最优值(min)、 平均值(avg)和标准方差(std)进行对比, 对比结果列于表2.

表2 不同算法对函数f3～f12的500维问题寻优结果对比

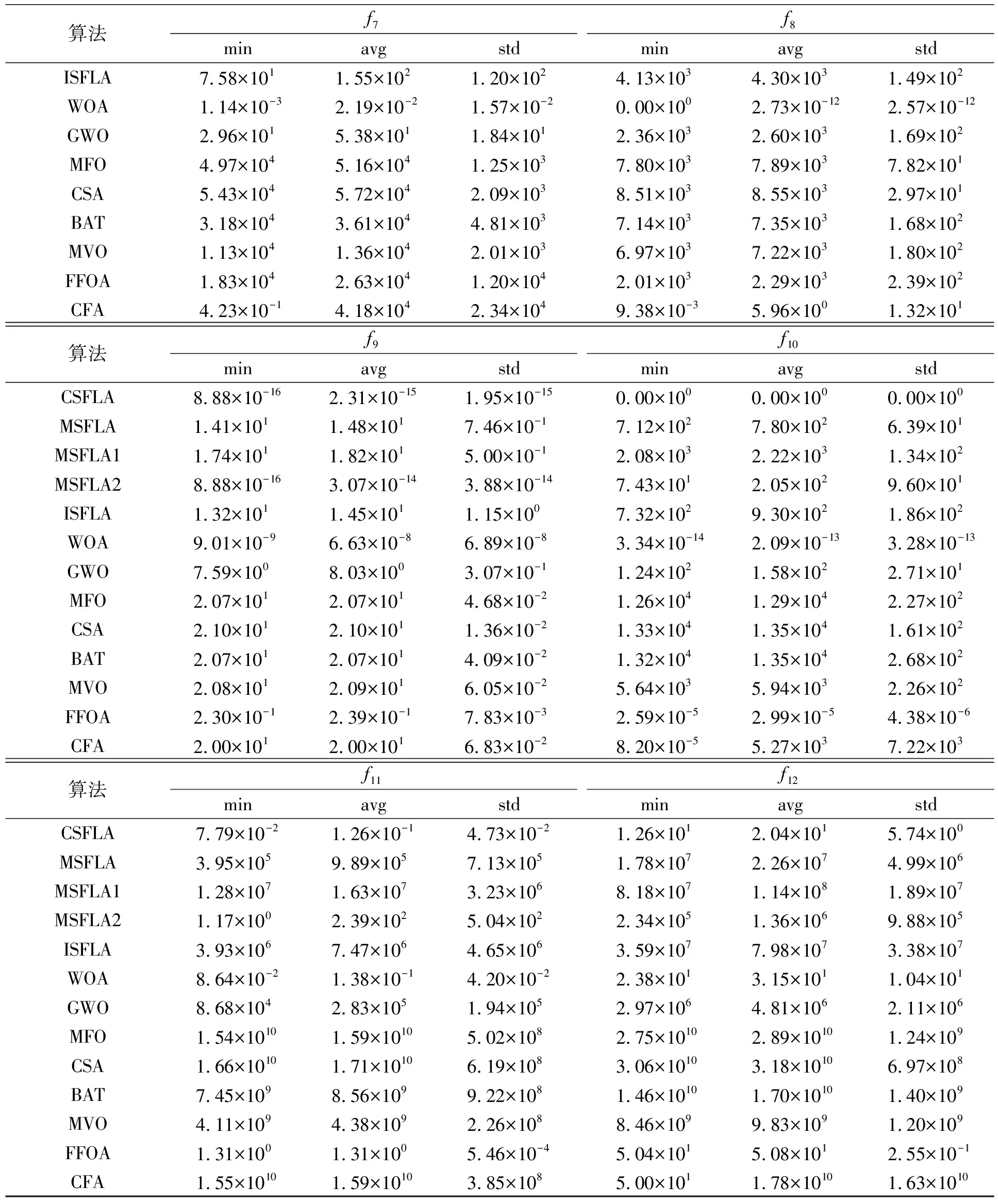
续表2

由表2可见, CSFLA性能优于其他算法. 对于f3,f4函数, CSFLA的寻优精度明显优于其他算法； 对于f8,f10函数, CSFLA均找到了全局最优解； CSFLA,WOA和FFOA对f5,f12函数的寻优结果数量相同; CSFLA和WOA对f6,f10,f11函数的寻优结果相似; CSFLA和MSFLA2对f7,f9函数的寻优结果相似, 但CSFLA平均值和标准差相对更好, 且进化次数明显优于其他算法. 其原因如下：

1) 引入信息空间指导群体空间进化, 有效记录了算法进化过程中形成的优秀经验, 同时对信念空间的个体利用螺旋方式在最优个体周围查找更优解, 并通过影响函数将优秀进化经验反馈到群体空间提供个体寻优性能；

2) 相对于基本蛙跳算法, CSFLA改进了最差个体的进化方式, 增加了最差个体的参考知识, 分别为子群最优、 种群最优和信念空间的知识, 较好地平衡了个体进行局部寻优和全局探索.

综上所述, 本文将文化算法理论与混洗蛙跳算法进行融合, 基于社会学理论改进最优个体的进化方式, 利用螺旋进化和随机游走的方式在最优个体周围寻找更优解, 同时利用种群最优、 子群最优和信念空间的知识平衡个体的局部寻优和全局探索. 通过对12个基准函数测试的结果表明, 该算法可用较少的迭代次数获取较优的结果, 尤其针对单峰函数寻优效果更明显. 所以本文算法可应用到适应值计算复杂度较大的优化问题中.