基于动量因子优化学习率的BP神经网络PID参数整定算法

胡黄水, 赵思远, 刘清雪, 王出航, 王婷婷

(1. 长春工业大学 计算机科学与工程学院, 长春 130012； 2. 吉林建筑科技学院 计算机科学与工程学院, 长春 130114;3. 长春师范大学 计算机科学与技术学院, 长春 130032)

PID(比例-积分-微分)控制算法是工业控制中的通用方法之一, 因其结构简单而广泛应用于冶金、 轻工和机械等工业控制中, 控制效果由PID参数决定[1-3]. 在实际工业控制中, 根据不同的控制效果需求用专家经验设置PID参数, 无法实时调整, 因此PID控制算法在非线性和复杂系统中应用效果较差[4-6].

近年来, 利用智能控制算法对PID参数整定成为研究热点, 如神经网络PID、 模糊逻辑PID、 遗传算法PID等, 这些智能控制算法均具有较强的学习能力[7-9]. 神经网络在智能控制、 预测控制[10-11]、 模式识别[12-13]和信号处理[14]等领域应用广泛. 其中BP神经网络具有并行分布式处理、 鲁棒性强和容错性强等特点, 并具有自适应学习和较强的逼近非线性映射能力, 因此神经网络PID控制算法是控制复杂系统的常用方法之一[15-16], 广泛应用于建模和控制较复杂的非线性系统[17]中. 但传统的BP神经网络在学习过程中学习率始终保持不变, 若学习率选取过小, 则每次权值的调整量小, 网络收敛速度慢； 若学习率选取过大, 则每次权值的调整量大, 而较大权值调整量可能导致网络在误差最小值处产生振荡现象, 网络因此变得发散而不能收敛[18]. 针对上述传统BP神经网络具有训练过程中易陷入局部极小值和收敛速度较慢的缺点, 研究人员已提出了各种改进的BP神经网络控制算法： 文献[19]提出了一种既可加快学习速度又可保持稳定的方法, 即在迭代公式中增加一个动量项, 可有效抑制网络训练中可能出现的振荡现象, 具有缓冲平滑的作用, 并有利于脱离平坦区, 加快训练速度; 文献[20]提出了一种添加多重动量项的方法, 该方法能有效减少网络训练次数, 加快收敛速度; 文献[21]提出了一种改进的BP算法, 该算法的动量系数根据当前的梯度最速下降方向和权值上一步的改变方向自适应变化. 为进一步加快神经网络的收敛速度, 在借鉴现有改进算法的基础上, 本文设计一种新的BP神经网络PID参数自适应整定算法, 该算法通过动量因子优化学习率和增加动量项抑制网络训练中由于学习速率选取过大可能导致的振荡现象, 优化了神经网络的收敛速度.

1 BP神经网络的PID控制

传统PID控制器属于一种线性控制器, 其原理是系统的实际输出值与期望值形成系统偏差, 通过对偏差量的调整控制目标. 传统PID的控制参数不能实时调整, 在实际控制中, 传统PID控制算法的稳定性、 时变性和自适应性控制效果较差, 且在非线性控制上效果不明显. 针对传统PID控制器的缺点, 本文将BP神经网络和PID控制器相结合, 利用BP神经网络在线自适应调整控制参数, 实现PID参数的最优组合, 从而提高系统稳定性, 取得良好的控制效果.

1.1 BP神经网络结构

BP神经网络结构如图1所示, 采用三层结构： 输出层、 隐含层和输入层, 其中j,i,l分别表示输入层节点、 隐含层节点、 输出层节点. 输入层的输入节点数目为4, 隐含层的隐藏节点数目为5, 输出层的输出节点数目为3. 输入节点对应系统的期望值、 实际值、 偏差和控制量, 输出层节点与PID控制算法的Kp，Ki，Kd3个参数一一对应.

1.2 BP神经网络PID控制器

BP神经网络单元和PID控制器单元组合成BP神经网络PID控制器, 其原理是BP神经网络根据系统当前的运行状态, 通过自学习和权系数的调整输出最优的PID控制参数, 从而使PID控制器的3个可调参数自适应改变, 其结构如图2所示.

图1 BP神经网络结构Fig.1 Structure of BP neural network

图2 BP神经网络PID控制器的结构Fig.2 Structure of PID controller based on BP neural network

BP神经网络输入层的输入量为

(1)

BP神经网络隐含层的输入量和输出量分别为

(2)

(3)

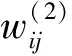
(4)

BP神经网络输出层的输入量和输出量分别为

(5)

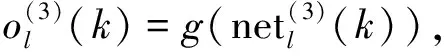
(6)

即

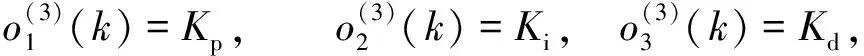
(7)

(8)

性能指标函数为

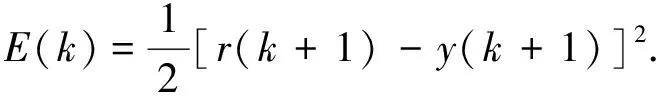
(9)

为加快收敛速度, 增加一个使搜索快速收敛到全局极小的惯性项, 根据梯度下降法修正神经网络权系数的公式[21]为

(10)

其中：η为学习率;α为动量因子. 由式(7)可得

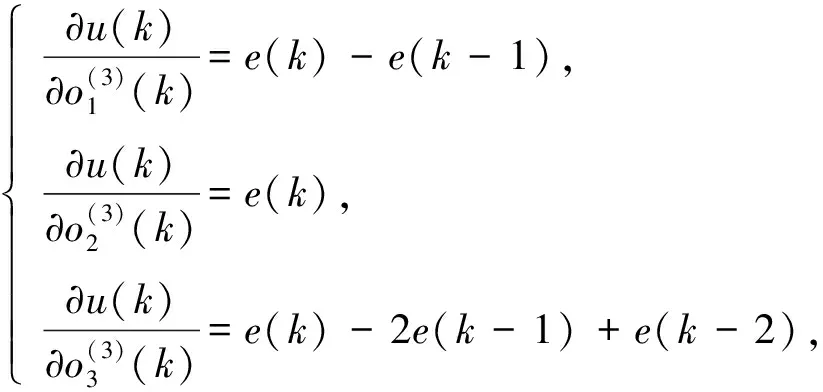
(11)

从而可得BP神经网络输出层权计算公式为

经典增量式PID控制器计算公式为

(13)

其中：Kp,Ki,Kd分别为PID控制器的比例、 积分、 微分系数；μ(k)为PID控制器输出量；y(k)为被控对象输出实际值；r(k)为系统期望值；e(k)为系统偏差.

2 改进的BP神经网络PID控制算法

传统BP神经网络在学习过程中, 学习率始终保持不变, 若学习率取值过大, 则较大的权值调整量可能导致网络在误差最小值处振荡, 使网络无法收敛[18].

为改进BP神经网络的性能, 本文添加了动量项, 并对其进行改进. 动量项的作用是记忆上一时刻连接权的变化方向, 增加动量项可得到较大的学习速率系数, 提高学习速度, 振荡现象可能出现在神经网络的训练过程中, 而动量项的“惯性效应”具有抑制振荡和缓冲的作用[20]. 权值的修正公式为

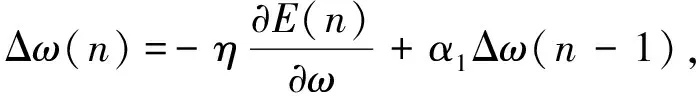
(14)

其中α1为(n-1)时刻的动量因子. 为进一步加快神经网络的收敛速度, 在其基础上增加(n-2)时刻的权值变化量, 改进后的权值修正公式为

(15)

其中α2为(n-2)时刻的动量因子. 添加(n-2)时刻动量项, 记忆前两个时刻连接权的变化方向, 可得到较大的学习速率系数, 以提高学习速度. 增加(n-2)时刻动量项后“惯性效应”更强, 抑制网络训练中可能出现的振荡能力也更强. 权值和误差的变化范围会随着神经网络训练过程进入误差曲面的平坦区域而减小, 从而可得

Δω(n)≈Δω(n-1)≈Δω(n-2),

将其代入式(15), 有

(16)

有利于加速脱离平坦区域.

通过上述改进后的BP神经网络结合PID控制器组成新的BP神经网络PID控制器(NBPPID), 其结构如图3所示.

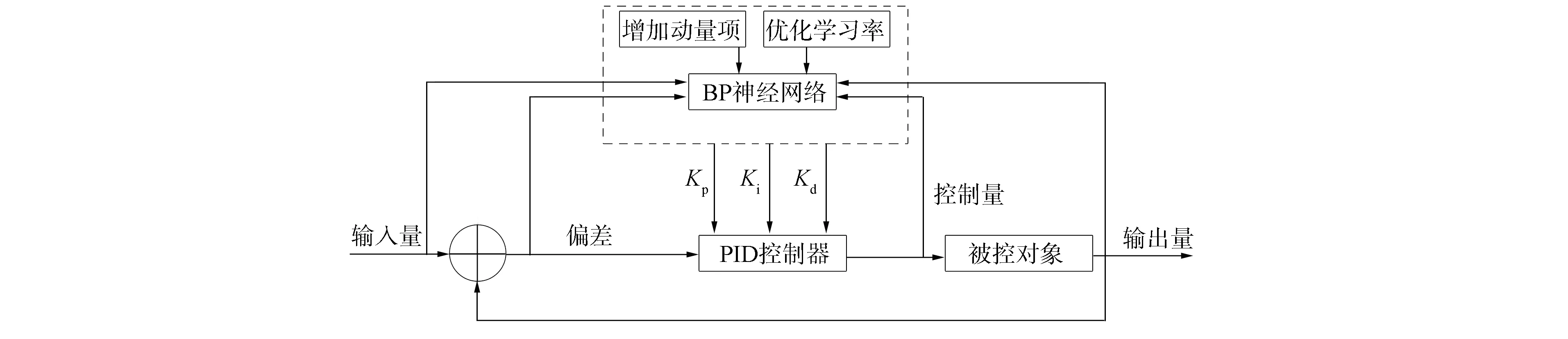
图3 改进的BP神经网络PID控制器结构Fig.3 Structure of PID controller based on improved BP neural network

改进算法步骤如下：

1) 确定BP神经网络结构, 初始化BP神经网络输入层、 隐含层和输出层权重系数, 并选择合适的动量因子α1,α2和学习率η, 令k=1；

2) 采样得到输入量和输出量, 并计算偏差量；

3) 确定BP神经网络输入层、 隐含层和输出层神经元的输入量和输出量, 其中PID控制器的控制参数Kp,Ki,Kd由输出层的输出量决定；

4) PID控制器输出控制量；

5) BP神经网络通过在线调整加权系数, 自适应调节PID控制参数；

6) 令k=k+1, 返回步骤1).

3 仿真分析

下面验证改进后的BP神经网络PID控制算法控制性能, 将改进的控制算法(NBPPID)与传统的BP神经网络PID控制算法(BPPID)和增加动量项的BP神经网络PID控制算法(MBPPID)进行对比. 利用MATLAB进行仿真实验, 取时变的非线性仿真系统[18]为

(17)

其中

a(k)=1.3(1-0.6e-0.2k).

图4 3种控制算法的输出曲线Fig.4 Output curves of three control algorithms

BP神经网络采用4-5-3的结构, 学习率η=0.2,α1=0.5,α2=0.1. 图4为3种控制算法的输出曲线, 其中rin为期望值. 由图4可见, 将NBPPID和MBPPID算法与传统BP神经神经网络PID控制算法相比均能有效缓解振荡现象, 且NBPPID先于MBPPID算法到达期望值, 加快了收敛速度. 图5为3种控制算法PID的控制参数曲线. 由图5可见, NBPPID控制算法PID控制参数最优值为

Kp=0.053,Ki=0.047,Kd=0.008.

综上所述, 本文提出了一种新的BP神经网络PID参数自适应整定算法. 该算法通过对学习率和动量因子进行改进, 利用动量因子优化学习率和增加动量项抑制网络训练中可能出现的振荡现象. 控制过程中, NBPPID控制算法自适应整定PID参数. 实验结果表明, 改进算法有效缓解了振荡现象, 并加快了算法的收敛速度.

图5 3种控制算法的PID控制参数曲线Fig.5 PID control parameter curves of three control algorithms