直流电源转换器系统的模糊跟踪控制

李 宁

（淮南师范学院 金融与数学学院，安徽 淮南232038）

1引言

直流降压电源转换器已经被广泛用于高压直流输电、直流电机驱动器、混合动力电动汽车、电动汽车等工业系统。许多学者对直流电源转换器的电压控制问题进行研究。提出的控制方法主要有：自 适 应 控 制［1］、反 步 控 制［2］、滑 模 控 制［3,4］、模 糊 控制［5］、有限时间控制［6］等。

许多实际系统往往有若干不确定因素存在，有时候系统控制增益是未知的。如何对控制增益未知的系统进行有效控制是需要解决的问题。借助Nussbaum-type函数［7,8］，可以有效解决该问题。但是利用Nussbaum-type函数设计的控制器比较复杂。受文献［9］启发，本文利用模糊系统设计控制器，通过自适应率线上估计未知常数，提出的控制器能保证闭环系统所有信号有界，同时能达到对希望信号的有效跟踪。

考虑如下直流电源转换器

其中，iL表示电路感应电流，νout和νin分别表示输出和外源电压，L表示电感，R表示负载电阻，C表示电容，μ∈［0,1］表示占空比函数.需要达到的控制目标是设计模糊控制器实现系统信号对目标信号有效跟踪。

2主要结果

为了便于讨论，做如下变换。

于是，得到系统的简介形式

其中，

定义逼近误差

定义滑模面

其中c是正的控制常数，满足微分方程e˙+ce=0的解e收敛于0.

对求关于时间的导数，得

设计理想控制器

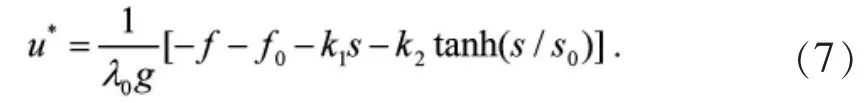
当取u=u*时，利用理想控制器（7），等式（6）可以简化为

k1和k2是设计常数.显然，t→∞时，有s→0，因此ei收敛于零，i=1,2。

但是，λ0，g和f可能是未知的，此时，理想控制器也是未知的.为了解决这个问题，利用模糊系统逼近理想控制器，即

其中ξ*是未知理想参数向量，w是模糊基函数，ε是逼近误差.由于ξ*是未知的，需要设计自适应率，用ξ逼近ξ*.设计实际控制器为

对等式（6）做如下变形

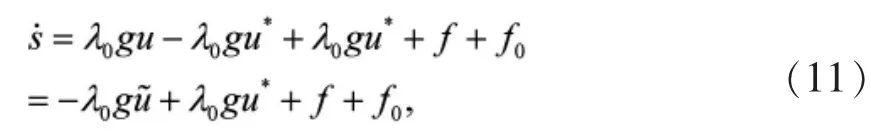
利用理想控制器（7）,（11）式可以变为

令λ=-λ0,则有如下等式

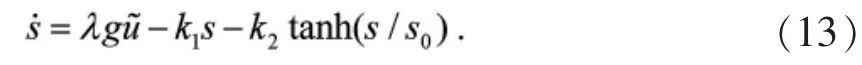
容易推出

即

构造Lyapunov函数

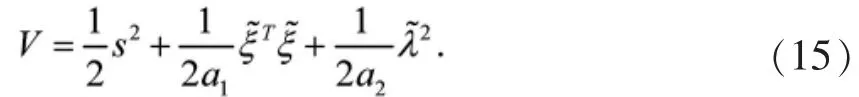
对V求关于时间t的导数，得

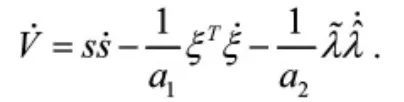
设计自适应率为

其中，a1,a2,σ1和σ2是设计常数.利用等式（16）和（17），显然有

显然有如下不等式

取正常数q＜1，可以得到

于是，有

其中，

下面给出主要结果。

定理 考虑系统（1），设计的控制器（10）和自适应率（16）,（17），能够保证闭环系统所有信号是有界的，同时跟踪误差渐近收敛到一个设定区域。

证明：对不等式（20）从到积分，得到如下不等式

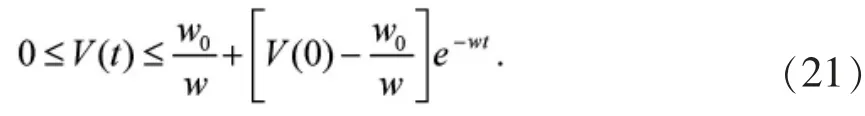
不等式（21）说明闭环系统所有信号是一致有界，同时s满足集合。也就是说s也是一致有界的。因此，逼近误差e渐近收敛到一个设定的区域内。

3数值仿真

考虑系统（1），取系统初始值νout（0）=3.2，iL（0）=0.3，系统参数R=10，C=20，L=0.3，控制参数K1=2，K2=2，c=0.3，a1=2，a2=1.5，σ1=0.0005，σ2=0.0005，c=2。设定系统不确定部分，系统扰动。利用matlab软件进行仿真，如图1-图4所示：

图1

图2

图3

图4

通过图1，可以看出，闭环系统信号有界。图2和图3说明跟踪误差渐近收敛于一个较小的设定区域。图4显示，控制器是有界的。

4小结

本文研究了未知控制增益系统的控制问题。在只知道系统状态的情况下，仅仅利用模糊系统逼近控制器和自适应率，就能实现系统对希望信号的有效跟踪，并且闭环系统所有信号有界。该方法具有结果简单，易于操作的特点。最后通过数值仿真验证了提出的控制方式的有效性。