一种适用于遥感图像的可逆信息隐藏算法
2020-11-26回征周诠
回征,周诠
中国空间技术研究院 西安分院,西安 710000
卫星遥感图像,在各个领域中发挥着不可或缺的重要作用[1]由于成像距离远,卫星遥感图像幅宽远大于普通光学图像,数据量庞大。然而,在如此庞大的图像数据之中,卫星遥感图像中亟需传递的目标区域或情报信息所占的比例却不高,较为次要的背景(海面、大气等)区域占据遥感图像中大多数部分。在传统遥感图像处理过程中,普遍只对图像的全局信息进行处理分析,这样一来,处理次要信息造成了不必要的计算开销,影响系统性能。以图像压缩为例,为了不在重构图像中引入过多失真而影响重要目标的获取,很难实现星地遥感图像高倍压缩;此外,全局处理方法,保留了大量次要区域的图像细节,既增加运算量,也是对传输链路资源的一种浪费。
在这种背景下,需要引入一种针对目标区域的非均匀处理技术,对遥感图像的背景和目标进行差异处理:保证重要目标的无失真传输,确保重要信息的传递;而较为次要的背景区域,则适当降低其重构视觉质量,以减少资源开销。近些年来随着人工智能技术的发展,借助于各类神经网络,遥感图像中的目标区域提取已逐渐成为现实[2-3]。
数字图像信息隐藏技术[4],利用数字图像中存在的冗余以及人类视觉的不敏感性,将秘密信息嵌入到载体图像中,并在接收端无误地提取出嵌入的信息。信息隐藏的这一特性,完美契合了上述非均匀遥感图像处理的需求。可逆信息隐藏(reversible data hiding,RDH)[5-6],是信息隐藏技术的一个重要分支。在RDH中,不仅秘密信息可在接收端准确无误提取,载体图像同样也可以恢复到原始状态。
Tian[7]在2003年提出的基于差值扩展(difference expansion, DE)的可逆隐藏是一类经典的RDH算法。DE通过哈尔小波,对像素对之间的整数差值进行扩展,得到冗余空间,可逆地嵌入秘密信息。许多研究学人员对DE算法进行了改进,主要包括两类方法,即基于整数-整数变换(integer-to-integer transform, IT)[8-11]和预测误差扩展(predict error expansion, PEE)[12-15]的可逆隐藏方法。其中,PEE通过扩展载体像素与预测像素的误差来代替直接扩展载体像素之间的误差,可在自然图像中生成更大的冗余空间,以获得更好的嵌入性能。总体来说,大多数基于DE的RDH算法都依赖一个二值矩阵,用以标记可扩展的像素对,称之为位置图(location map)。位置图需要使用无损二值压缩(如JBIG)进行处理,并将压缩后的位置图作为辅助信息,与纯载荷(pure payload)一起嵌入载体图像中。也就是说,DE类算法的嵌入容量一定程度上受到定位图的可压缩性能制约。
直方图移位(histogram shifting, HS)是另一类有效的RDH方法[16-18],最早由Ni[16]在2006年提出。HS首先生成载体图像的灰度直方图,寻找其峰值点和零点,通过整体搬移直方图实现秘密信息嵌入。HS方法实现简单,计算复杂度低,其隐秘图像具有很高的视觉质量。但是,该方法的隐藏容量取决于载体图像的灰度直方图的峰值点。针对不同的图像,隐藏容量并不稳定,特别是当载体图像灰度直方图较为平坦时,该类方法的隐藏容量相当有限。此外,当载体图像不存在真正零点时,需要构造零点,而原有坐标则被记录下辅助标记定位信息,这些定位信息也需要额外的无损二值压缩。
将PEE与HS进行结合也是一种高效的可逆隐藏方法。在这类方法中,将HS中直方图搬移的隐藏思想应用于PEE中生成的预测差值直方图,可以获得更高的隐藏容量。Luo等[19]使用PEE方法首先生成载体图像预测差值的统计直方图,并选取两个峰值点,向不同方向进行直方图搬移实现可逆隐藏。 Hong等[20]提出了一种基于预测误差修正(modification of prediction errors, MPE)方法。由预测误差域构造出的直方图具有更明显的峰值点,在相同隐秘图像质量前提下,该方法只需要修改较少的预测误差值,就可获得高于传统HS的嵌入容量。
在星地遥感图像的传输过程中,嵌入了秘密信息的隐秘图像是视觉不可见的。也就是说,在设计相应可逆隐藏算法过程中,可以突破隐秘图像不可感知性的限制,在提取的目标区域中,可逆藏入尽可能多的秘密信息。此外,遥感图像传输对实时性要求很高,对算法的时效性要求很高。综上所述,适用于遥感图像非均匀处理的RDH算法应具备两个特点:1)不考虑隐秘图像视觉质量的情况下,嵌入尽可能多的秘密信息;2)简单有效,具有较好的时效性。
若将应用现有的RDH算法非均匀处理,存在以下问题:1)单次嵌入量不足。受限于载体图像不可感知性的限制,现有的可逆信息隐藏算法中,每一次秘密信息嵌入时,载体图像像素的修正程度都很小,所能嵌入的秘密信息容量较少。2)需要额外无损压缩处理辅助信息。通过回顾各类经典的可逆信息隐藏算法可以看出,辅助信息,特别是对溢出像素的标记,是其中不可或缺的重要部分,这无疑与星地遥感图像处理的实时性要求有所冲突。
本文针对遥感图像传输的特点,提出了一种基于目标的非均匀处理方法,选取遥感图像的目标区域及其邻域为载体(假设目标可由其他算法进行提取),将背景区域进行高倍图像压缩形成码流,该码流经过加密后可逆的嵌入载体。在该方法中,载体的不同子块的像素通过与块内基准像素进行运算,分为平滑块和复杂块,秘密信息被嵌入在平滑块内除基准像素之外的像素之中。在接收端,修改过的像素可通过该块内的基准像素进行完全复原。与传统RDH算法比较,该算法具有单次嵌入容量大、实现简单及无需额外二值无损压缩的特点。
1 算法流程

图1 基于RDH的遥感图像非均匀处理方法Fig.1 The RDH-based non-uniform process of remote sensing images
基于RDH的遥感图像的非均匀处理流程如图1所示。本文假设目标可以由特定方法正确提取,现有针对遥感图像的目标检测算法包括视觉显著性检测[21]、基于机器学习的方法及基于深度学习的方法[2-3]等。随后背景区域经过高倍压缩——如压缩标准JPEG2000。随着近年来人工智能的发展,各类神经网络压缩方法也使高质量高倍图像压缩成为现实[22]。
在阐述算法之前,先定义两种图像像素的位运算,对于非负整数0≤x≤255以及二进制数字b∈{0,1},定义以下位操作算子:
b=bitget(x,r),r∈[1,2,…,8]
(1)
x*=bitset(x,r,b),r∈[1,2,…,8]
(2)
算子表示的是提取像素x的第几位。例如对于8 bit量化的灰度图像,r=8代表其最高有效位(most significant bit,MSB);与此相反,r=1代表其最不显著位(least significant bit,LSB)。此外,bitset(·)算子是将像素的第r比特替换为b,如bitset(127,8,1)=255。
1.1 秘密信息嵌入
首先对将载体图像进行分块,利用给定正整数门限T=2t以及每个图像块中的基准像素,对该像素块的平滑程度进行判别。然后,载体图像中的每个图像块都可归类为平滑块以及复杂块,这种判定得出平滑性由选定基准图像的LSB表示,而原有基准像素的LSB则作为辅助信息,与纯载荷共同构成秘密信息,隐藏在平滑块中。秘密信息的嵌入通过比特替换进行,嵌入过程具体如下:
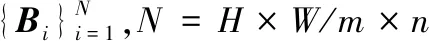
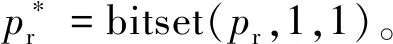
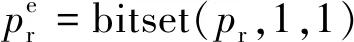

当第一遍扫描结束后,得到需要嵌入载体的秘密信息为X=A∪P,其中P为纯载荷。

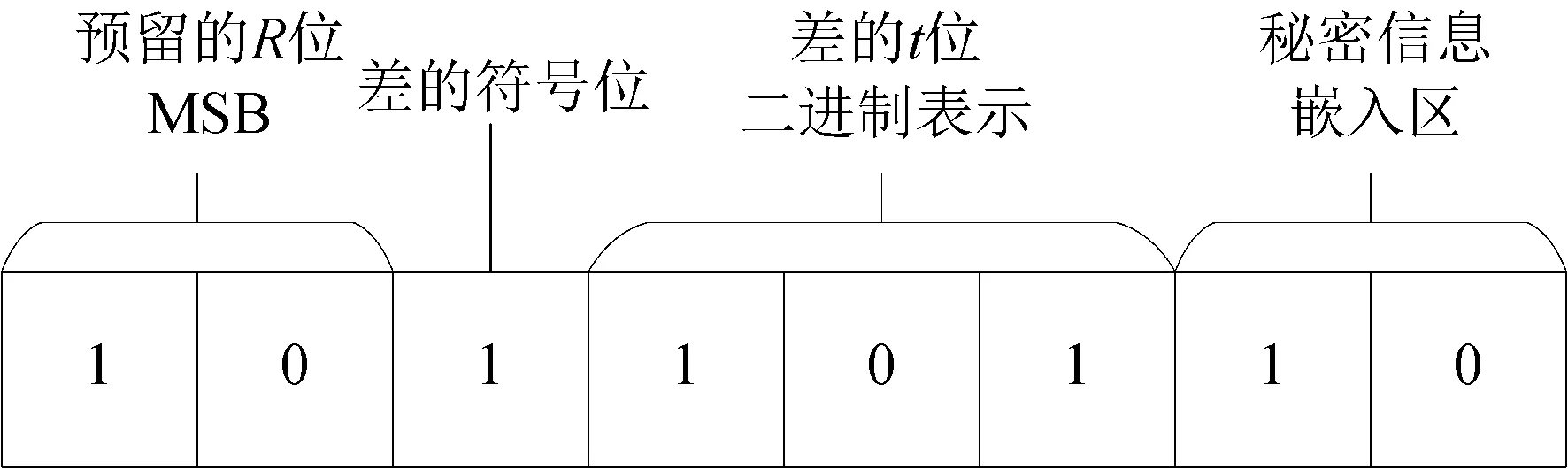
图2 修改后像素的位结构Fig.2 Bits of the modified pixel
Step 4.2如果f=0,那么Bi为复杂子块,跳转至下一子块。
循环至所有子块都进行嵌入,完成秘密信息的嵌入过程,得到隐秘图像Ie。
1.2 秘密信息提取
与嵌入过程类似,秘密信息的提取可以看作是嵌入的近似逆向过程。其主要过程包括对隐秘图像分块,提取每个子块中的基准像素,根据预先设置的LSB判决该子块是平滑块还是复杂块。对于平滑子块,提取除基准像素之外每块像素的8-R-(t+1) 位LSB,即为嵌入的秘密信息,并解码其中(8-R)~(8-R-t)位(t+1)bit,转化为十进制差值,与基准像素做运算恢复该位像素。当所有秘密信息提取完毕后,使用其前N位辅助信息,对各个子块(包括平滑以及复杂块)标记修改的基准像素进行复原,完成最终的载体图像,保证隐藏算法的可逆性。秘密信息提取以及载体图像复原的具体步骤如下:
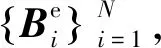
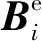
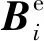

1.3 嵌入容量分析
由上文嵌入算法可见,本文方法中,可供秘密信息嵌入的冗余空间由平滑子块提供,而每一个子块,包括复杂子块中的基准像素的LSB都需要记录下来,作为附加信息用于载体复原,对于 像素的8 bit灰度载体图像,假设共有Ns个平滑子块,则嵌入的秘密信息纯载荷共有:
count(P)=Ns×[8-(t+1)-R]·
(3)
其中,count(P) 指的是纯载荷数据P的大小,[8-(t+1)-R]为块中除基准像素之外每像素可以隐藏的比特数,(m×n-1)为每块中可供隐藏像素的数目,t=「log2T⎤与门限T相关,R为像素预留MSB,M×N/(m×n)为提取的各个子块中预留的LSB个数,这些提取出的LSB构成了附加信息A,用于基准像素复原。
式(3)中,预留MSB数R与载体图像大小H×W为定值,而平滑子块数目Ns由t与m×n共同决定:当子块大小m×n一定时,(m×n-1)与M×N/(m×n)一定,而t越大,平滑子块数目Ns越多,但每像素中可隐藏的比特数[8-(t+1)-R]则会下降;另一方面,当t一定时,每像素隐藏可隐藏[8-(t+1)-R]bit信息,子块大小m×n越大,每个子图像块中隐藏的信息比特数[8-(t+1)-R](m×n-1)越多,附加信息总量H×W/m×n越少,但平滑子块数目Ns会随着m×n增大而减小。
最后,如图1中所阐述,需要对背景区域进行压缩,而其压缩比由目标区域所能嵌入的秘密信息容量决定,当然,可以对图像进行两次扫描计算得出精确的嵌入量,但这增大了系统的开销。一种可行的方法是使用特定样本的图像集,预估出目标区域的某些简单特性与嵌入容量的关系,在每次输入图像时,计算估计出可嵌入的容量,得出相应压缩比。
本方法的嵌入容量与载体——目标区域的自身特性息息相关,即含有较多平坦区域的载体,容量更高;而含有更多纹理和细节的载体,嵌入容量较低。在这里,使用图像活性度量(image activity measurement,IAM)[23]对给定图像I的平滑性进行预估,IAM的定义如下:
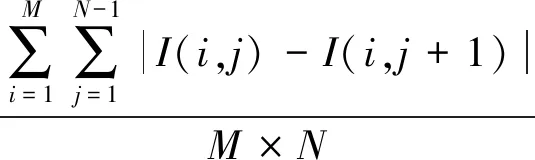
(4)


(5)
通过得到该参数下(门限,分块大小)的一系列多项式系数pi对于每一个输入图像,就可以估计出其在不同门限下的嵌入容量。
得到适当拟合系数之后,每一次的输入图像,只要得到其IAM值,就可以带入不同多项式,预估最佳的嵌入容量:

(6)
随后,根据预估的嵌入容量,即可进一步计算出背景区域所需的压缩比。
2 试验结果及讨论
为了测试算法性能,首先选取了6张512×512 大小的灰度遥感图像(见图3)。后续试验主要对算法的嵌入容量进行测试,嵌入容量通常由直接嵌入的信息比特数衡量,其单位为bit。

图3 测试遥感图像Fig.3 Standard test images
上文分析过,本算法的嵌入容量主要受两个因素影响:分块大小m×n和门限T,在这里设置了9种不同分块方案以及4类不同门限大小。不同参数下(m×n和T),6幅测试图像的单次嵌入容量如图4所示。由图4可以看出,对于所有图像,当门限T=64时,隐藏容量都处于较低的水平,这是因为门限取值较大时,虽然平滑子块数目Ns较大,但每个可隐藏像素与基准像素之间的差值,其二进制编码会占据更大的空间,导致每个可隐藏像素实际嵌入的纯载荷数量下降。
对于分块大小m×n,当子块较小(m<4且n<4)或是子块较大时(m>4或n>4),各个测试图像得出的隐藏容量都处在相对较低的水平,而对于分块m=2,n=4,m=4,n=2和m=4,n=4,试验得出的隐藏容量处于一个大致相当的水平。
综上所述,对于含有大量背景,即平滑区域的遥感图像,可选区较小的门限T=16来最大化嵌入容量。在下文算法对比中,本方法的参数设置为T=16,m=2,n=4。
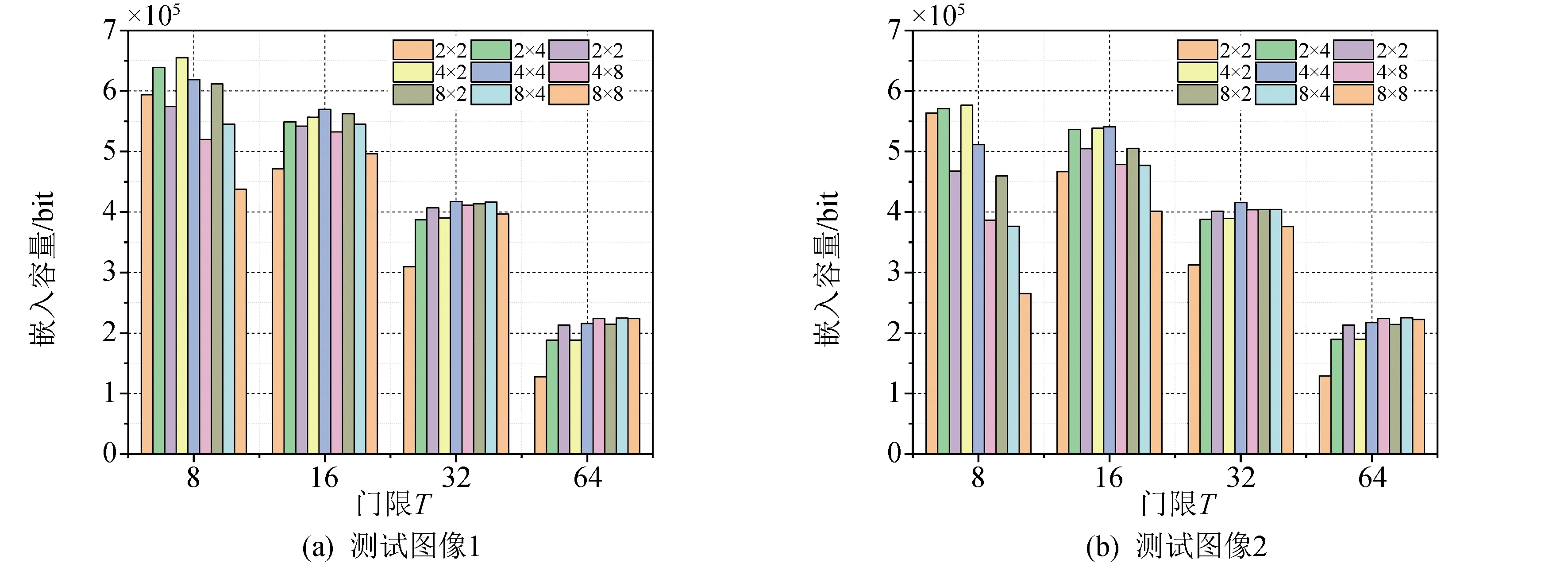
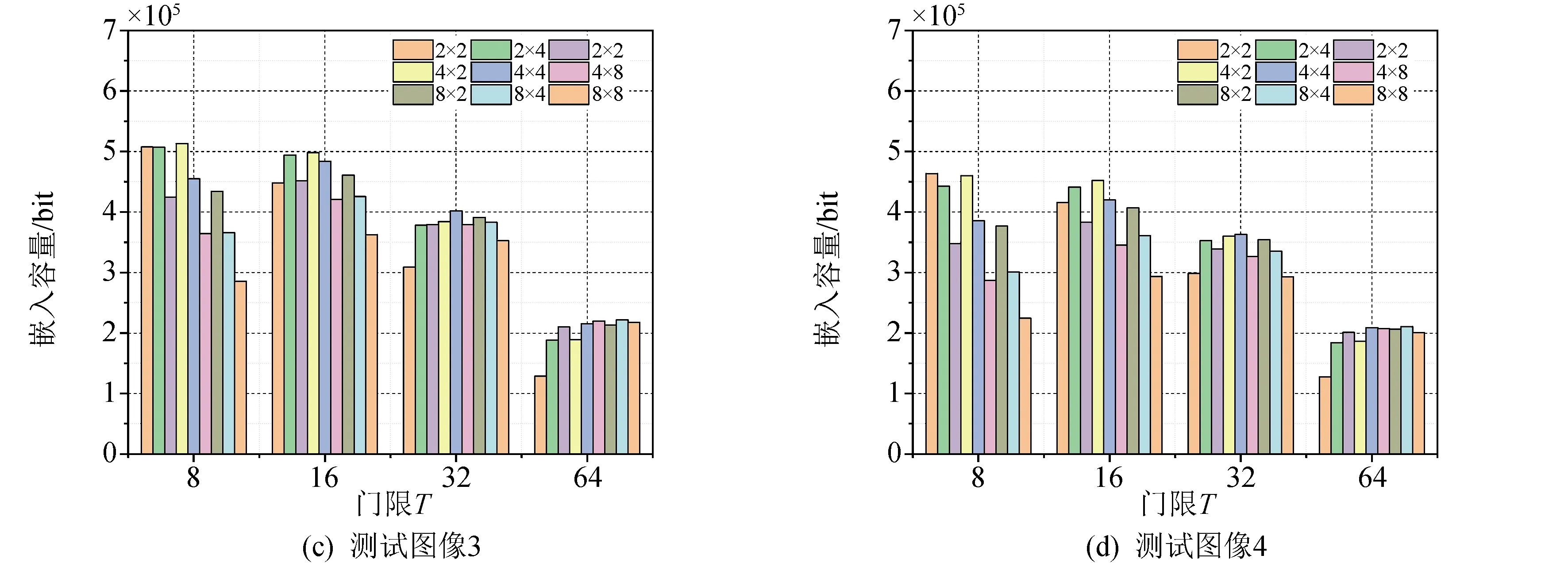

图4 不同参数下,各测试图像的单次嵌入容量Fig.4 The capacity of test images at singe embedment in different parameters
这里选取一些典型空域可逆信息隐藏算法,包括Ni[16],Li[15],Hong[20],Luo[19],Hu[13]以及Coltuc[11],对不同算法的单次嵌入容量进行比较。

图5不同RDH算法之间单次嵌入容量比较Fig.5 Comparison of RDH schemes for capacity at single embedment
通过图5可以看出,对于所有6幅测试遥感图像,本文方法的隐藏容量具有很大的优势,相比于基于IT(基于IT变换的可逆隐藏算法一般更适宜与大容量可逆隐藏)的Coltuc算法,本文方法的隐藏容量可以达到250 000~450 000 bit的优势。由此可见,对于具有较多背景区域的星地遥感图像,本文方法仅需要进行一次嵌入,就可以得到400 000~650 000 bit的嵌入容量,而这一过程是完全可逆,在接收端可以完全复原载体图像和秘密信息。
本文和对比算法的辅助信息处理方式如表1所示。从表1可以看出从,除Coltuc算法,其他基于DE、HS和PEE的算法都依赖于额外无损二值压缩进行辅助信息处理,而本算法嵌入和提取过程中,无需进行额外的无损二值压缩。综上所述,本文方法可以在不进行重复迭代,在仅需一次嵌入情况下,在512×512测试遥感图像中藏入400 000~650 000 bit秘密信息。此外,对于可逆隐藏所必须的附加信息,本文方法不需要进行额外的无损压缩处理。

表1 现有RDH隐藏算法的辅助信息处理方法
为了进一步探究,将本方法应用于遥感图像时的性能,本文选取了WHU-RS19遥感图像集中的200张512×512像素遥感图像。所选取门限T=16以及T=32,分块大小包括m=2,n=4,m=4,n=2,m=4,n=4 共6种情况,200张图像的隐藏容量分布以及数值统计结果,如图6所示。
由图6可以看出,对于所选遥感图像,由于其大多数图像内容为平滑的背景区域覆盖,采用较小门限T=16时,即有足够的子块被判别为平滑子块,而显然T=16时每一个可隐藏像素所能提供隐藏空间要优于T=32时。当T=16时,对不同分块大小,平均隐藏容量相差不大,其中m=4,n=4时,平均嵌入量要高于另两种分块方式约5 000 bit,但在这种情况下,各样本隐藏容量之间标准差,不同图像所能提供的隐藏容量差异较大。
前文说过,进行背景区域压缩时,需要通过对现有图像集进行曲线拟合得出相应参数,预估嵌入容量及背景区域的压缩比,这里依然选取了使用的WHU-RS19中的200幅遥感图像,在分块方式为m=4,n=2,门限T=16以及T=32时,使用三次多项式拟合,拟合出图像IAM与嵌入容量的关系曲线,如图7所示。
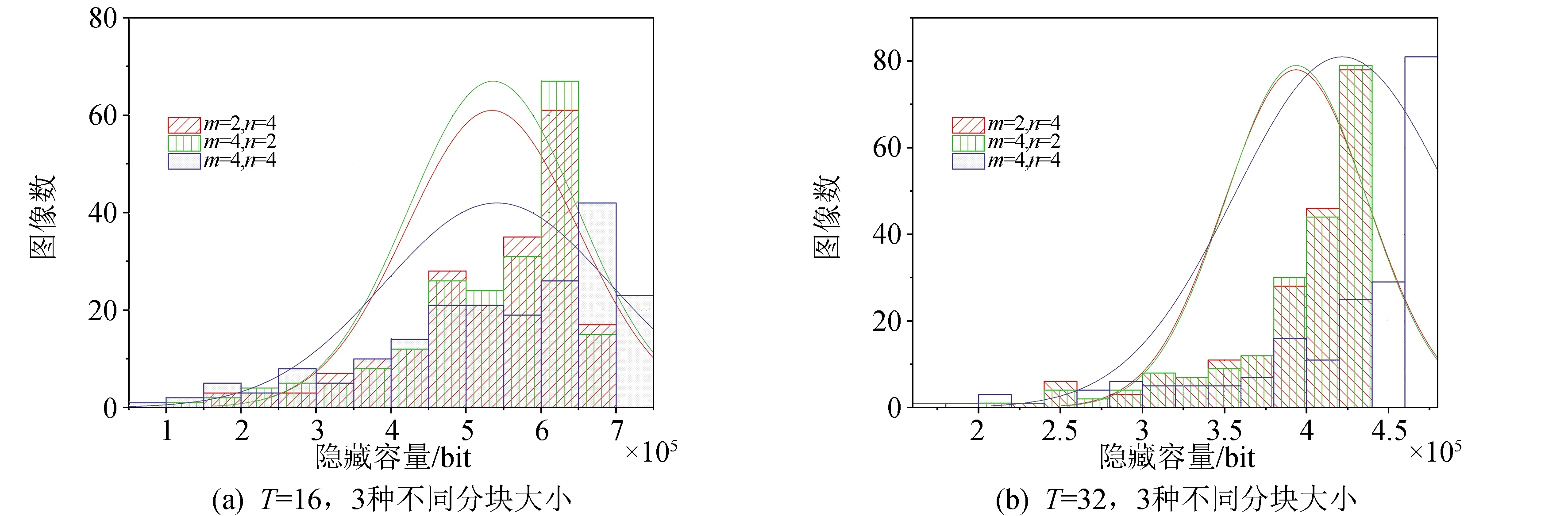
图6 不同门限下200张测试图像的单次嵌入容量分布Fig.6 Distribution of 200 test images′ capacity at single embedment under different thresholds
由图7可以看出,随着IAM的增大,算法的嵌入容量会逐渐变小,嵌入容量是IAM的减函数。在IAM较小(IAM≤10)——即图像拥有较多平坦区域时,曲线的拟合程度较高,嵌入容量-IAM点集中在拟合曲线附近。相对于门限T=16,当T=32时拟合误差更小,曲线拟合程度更好。同时,T=32时,嵌入容量随IAM的变化程度更小,均值较T=16更小。

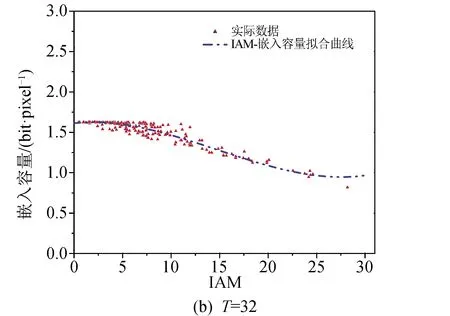
图7 不同参数下,测试图像的IAM-嵌入容量的 三次多项式拟合曲线。Fig.7 The cubic polynomial fitting curve of IAM versus embedding capacity in different parameters
3 结束语
本文提出了一种适用于遥感图像传输的大容量可逆信息隐藏算法:
1)算法可实现优异的单次嵌入容量,对于512×512像素的灰度测试遥感图像,平均单次嵌入秘密信息可达350 000~600 000 bit;此外,算法不需要借助额外无损压缩方法来处理辅助信息。
2)算法的最优性能需要通过调整多项参数才能达到,现阶段只能通过曲线拟合的经验曲线进行预估,尚不能达到根据输入图像进行准确参数调整。
3)与传统可逆信息隐藏算法不同,遥感图像传输过程中不需要考虑隐秘图像的视觉质量,脱离了隐秘图像视觉质量限制,可有效增加算法的单次嵌入容量。
4)通过本算法,可实现遥感图像目标区域在星地链路上的无损传输。
5)目前本方法尚在计算机仿真阶段,下一步将硬件验证算法的可靠性。
