利用星地差分GPS的地基测控系统实时标校方法
2020-11-26彭震金小军莫仕明张伟徐兆斌金仲和
彭震,金小军,莫仕明,张伟,徐兆斌,金仲和
浙江大学 微小卫星研究中心,杭州 310027
航天测控系统是航天活动中不可缺少的重要组成部分,用于对空间航天器进行跟踪、遥测和控制。对地基测控系统测量误差的标校是航天测控系统正常工作的必要环节,其目的是标定地基测控系统测量数据的系统误差,用标定的系统误差去修正测量数据,使地基测控系统的残余系统误差达到最小,从而使测量数据只受随机误差的影响[1-2]。
目前地基测控系统的标校仍主要采用传统的标校方法,主要包括标校塔标校、信标球标校和飞机标校等[3]。传统标校方法存在以下缺点:1)标校后残余误差仍然较大;2)不能反映在轨飞行任务的真实误差特性;3)不能处理在轨运行阶段测量误差的时变特性。大量在轨航天任务表明,传统标校方法标校后的地基测控系统的系统误差仍大于10 m,速度误差在5 cm/s以上[3]。这样的标校精度显然无法满足未来地基测控系统高精度测量的要求。
基于标校卫星和星地差分GPS的地基测控系统测量误差标校方法是克服以上传统方法缺点的有效途径。这种标校方法采用装载了星载GPS接收机的卫星作为标校卫星平台,与装载于地面测控站的GPS接收机形成星地差分系统,获得的高精度星地基线估计结果作为参考基准对地基测控系统测量误差进行校准。而与基于非差GPS定轨的标校方法相比,这种星地差分GPS方法的优点包括:1)无需精确已知地面卫星跟踪站坐标。2)星地差分GPS方法可以消除导航星钟差、接收机钟差对基线估计结果的影响。3)利用GPS载波相位观测数据,可获取高精度的星地基线估计结果。
文献[4]提出了一种利用星地差分GPS实现地基测控系统测量误差事后标校的方法,与传统误差标校方法相比,标校精度得到显著提升。但该研究主要存在两点不足:首先,该方法是一种事后标校方法,不能应用于对实时性有较高要求的场合,明显限制了应用范围。而通过实时标校,地基测控系统能及时获取标校后的测量数据,以解算得到实时的高精度定轨结果,从而使地面系统能实时进行轨道预报,并及时上注以提升星上姿轨控等系统的运行性能。因此,对地基测控系统的实时标校对于保障航天任务具有重要意义[5]。其次,文献[4]仅仅给出了试验结果,并未针对星地长基线场景对星地差分GPS估计的误差源进行深入分析,无法为工程实现提供理论支撑。
鉴于此,本文提出了一种利用星地差分GPS对地基测控系统进行实时标校的方法。该方法是在地基测控系统实时标校领域的首次应用。将星地基线的实时解算结果作为基准,采用标校处理算法实现对地基测控系统测量误差的实时校准。论文的另一个贡献在于针对星地长基线、高动态和实时标校场景,深入分析了影响实时星地基线解算精度的各误差源以及经误差补偿后的残差,并提出相对位置精度因子的概念,由此得到较为准确的星地基线实时估计的理论预测结果。通过半实物仿真对基于差分GPS的实时星地基线方法进行了验证,并应用于地基测控系统测量误差的误差标校之中。
1 基于星地差分GPS的实时标校方法
基于星地差分GPS的实时误差标校方法中,比较基准系统为星地差分GPS系统,被标校系统为地基测控系统。将实时星地基线估计结果与地基测控系统测量数据进行匹配处理,求解地基测控系统测量误差模型,以标定地基测控系统测量的系统误差。地基测控系统测量误差实时标校的总体方案如图1所示。
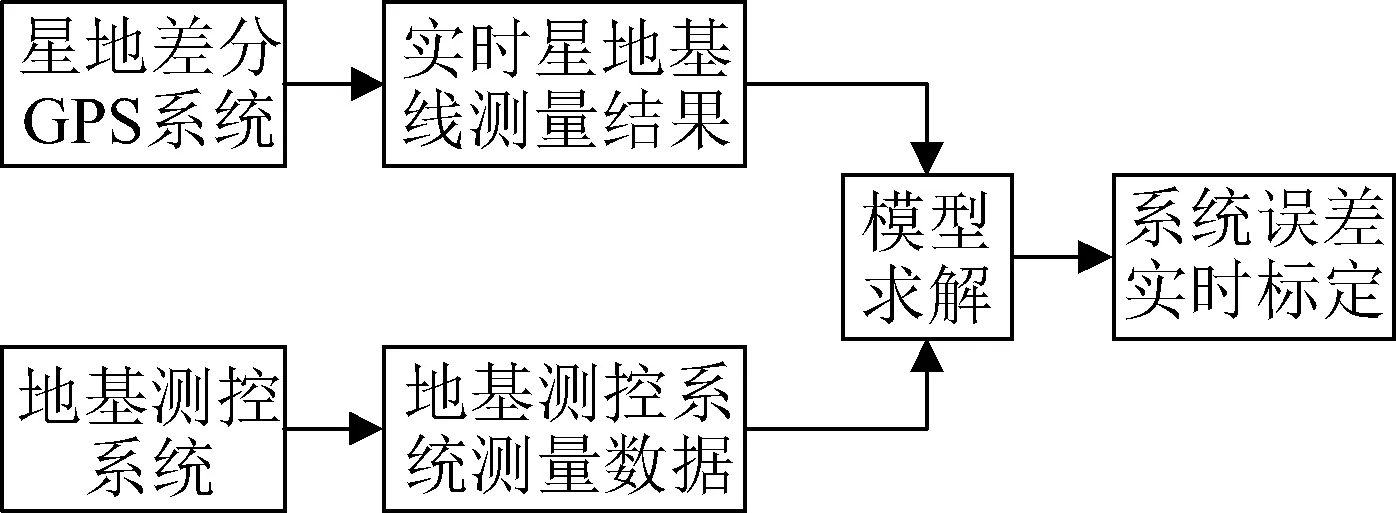
图1 测量误差标校总体方案Fig.1 Overall scheme of measurement error calibration
1.1 实时星地基线估计算法
星地标校场景存在基线长、低轨卫星动态大等挑战,导致GPS卫星共视条件差,差分数据质量差。为此,实时星地基线解算采用抗差自适应扩展卡尔曼滤波算法[6]。抗差自适应扩展卡尔曼滤波算法包括时间更新和测量更新两部分。
时间更新:
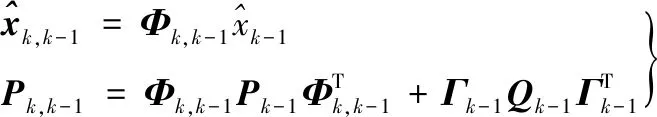
(1)

测量更新:
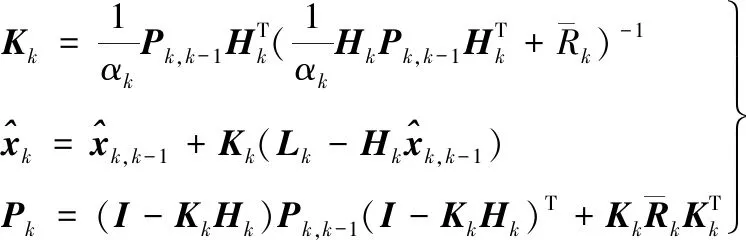
(2)

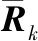
1.2 地基测控系统测量误差的实时标校
基于星地差分GPS系统获取实时星地基线估计结果,并将其转换为星地间距离、径向速度值,以作为地基测控系统测距、测速数据的比较基准。然后,基于加权最小二乘估计方法求解地基测控系统测距、测速模型,从而完成对测量系统误差的校准。
地基测控系统测距和测速误差模型可以分别表示如下[8-9]:

(3)
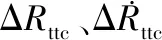
设备时延引起的距离误差可记为下式,a0作为误差模型的待求解参数:
a0=cΔτ
(4)
时间偏差引起的Δρtag为:
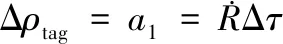
(5)

标校过程中,对流层延迟误差Δρtrop和电离层延迟误差Δρion通常采用模型改正,模型改正值分别记为Δρtrop,0和Δρion,0,残余的对流层延迟和电离层延迟误差之和表示为Δρres,可表示为观测仰角的函数。具体如下:
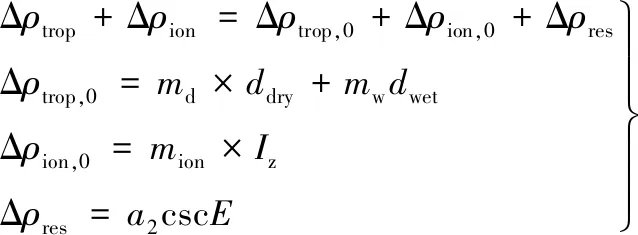
(6)
式中:md、mw分别为对流层干分量和湿分量延迟映射函数;ddry、dwet分别为天顶方向干分量和湿分量延迟;mion为电离层映射函数;Iz为天顶方向电离层延迟;E为观测仰角;a2为测距误差模型的待求解系数。
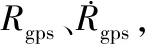
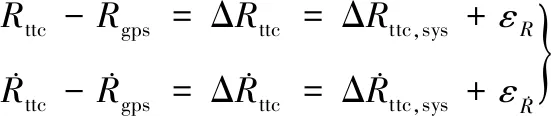
(7)

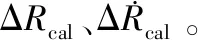

(8)

2 实时星地基线估计性能分析
基于差分GPS的实时星地基线估计属于长基线条件下的基线估计,星地间观测误差相关性较弱,而且在实时处理的限制下,无法使用IGS等机构的精密星历产品[11]。因此,需要对实时星地基线估计中各项误差的改正方法进行研究,并在此基础上对实时星地差分GPS系统所能提供的基线估计精度进行预算。从而为工程实现提供理论支撑。
2.1 实时星地基线主要观测误差及其改正方法
实时星地基线观测误差主要包括广播星历误差、电离层延迟、对流层延迟等。以下将从伪距、载波相位基本观测模型出发,采用控制变量法,逐一分析某一误差源在星地伪距、载波相位观测值上的等效距离误差。
在实时标校场景中,星地基线长达数千千米,星地观测相关性弱,差分对提升基线测量性能的作用不如近距离时明确。为了使得对观测误差的分析更加可靠和符合实际,在分析过程中采用SPIRENT GSS9000导航信号模拟器产生低轨卫星到导航星以及地面站到导航星的伪距、载波相位观测数据真值。低轨卫星和地面站之间构成一组星地基线。
(1)星历误差
事后星地基线估计算法中可采用IGS等机构的精密星历产品进行改正,而实时星地基线估计只能采用广播星历,通常其误差在1 m左右[12]。广播星历是影响实时星地基线估计精度的主要因素之一。实时星地差分GPS系统中,当其他误差源已知的情况下,米级星历误差在双差伪距、载波相位上的等效距离误差方程为:
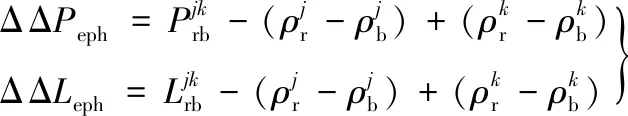
(9)
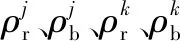
利用星历误差的等效距离误差方程,分析模拟器星地场景下星历误差的影响。可得星历误差在双差观测值上的等效距离误差及对应基线长度,如图2所示。
由图2可知:1)星历误差的等效距离误差大小与星地基线距离正相关。2)星地基线距离在3 000 km以内时,星历误差的等效距离误差处于20 cm以内。3)星地差分一定程度上削弱了星历误差的影响,由米级减小到20 cm以内。
因此,实时星地基线估计中,星历误差所引起的双差观测的等效距离误差可按20 cm估计。
(2) 电离层延迟及改正方法
实时星地差分GPS系统中,由于星地基线长,低轨卫星和地面站观测方向上电离层误差相关性弱,差分无法较好地消除电离层延迟。此外,Klobuchar电离层模型、单层电离层模型等[13-14]只适用于地基GPS观测的电离层延迟的改正。故本文采用伪距、载波相位的双频消电离层组合消除电离层延迟一阶项的影响。通常,电离层高阶项的影响仅为毫米量级[15-16]。双频消电离层组合模型可表示为:
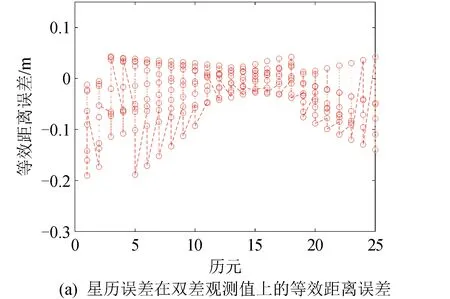
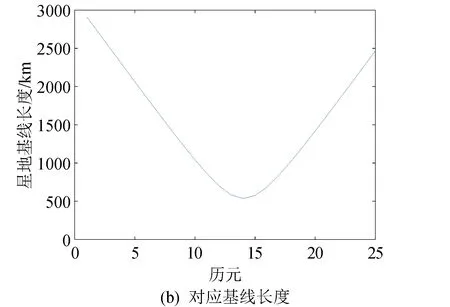
图2 星历误差的等效距离误差Fig.2 The equivalent distance error of the ephemeris error
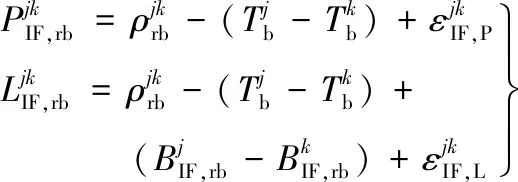
(10)
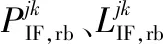
利用双频消电离层组合模型对电离层延迟进行改正,改正后电离层延迟在星地基线伪距双差观测值中对应的等效距离误差如图3所示。在星地长基线、高动态场景下,双频消电离层组合后,电离层延迟在双差观测值上的等效距离误差仅为毫米量级。
(3)对流层延迟及改正方法
实时星地差分GPS系统中,低轨卫星不受对流层的影响,而地面测站受对流层延迟的影响,星地差分无法消除对流层延迟,需将对流层延迟作为未知参数进行求解。地面测站观测方向上对流层延迟模型可表示为[17]:

图3 电离层延迟改正后的等效距离误差Fig.3 The equivalent distance error after correction of ionospheric delay
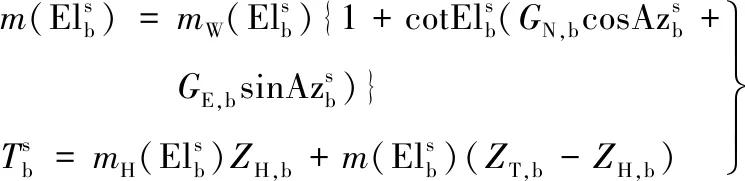
(11)
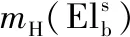
对流层天顶方向干分量延迟采用Saastamoinen模型改正,天顶方向湿分量延迟表示为天顶方向总延迟ZT,b与天顶方向干分量延迟ZH,b的差,式(11)中的映射函数均采用NMF模型。本文将对流层天顶方向总延迟ZT,b和梯度参数GN,b和GE,b作为滤波估计的未知参数,以吸收对流层延迟对星地基线解算的影响。
采用该对流层参数估计方法后,对流层延迟在双差伪距、载波相位观测值上的等效距离误差如图4所示。
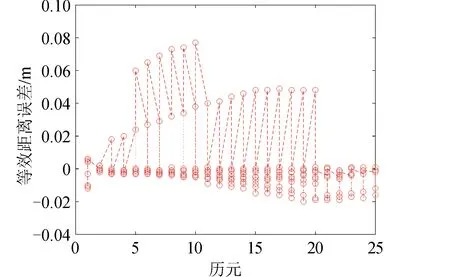
图4 对流层延迟改正后的等效距离误差Fig.4 The equivalent distance error after correction of tropospheric delay
由图4可知,对流层延迟参数估计后,对流层延迟在双差观测值上的等效距离误差多数在2 cm以内,极少数卫星的等效距离误差可达10 cm左右。因此,实时星地基线估计中,对流层延迟误差所引起的双差观测的等效距离误差可按10 cm估计。
(4)其他观测误差的改正方法
对于星载GPS天线相位中心相对于标校卫星质心的偏差与变化,可在标校卫星装配完成之后测定。
除此之外,导航星钟差、接收机钟差由差分的方法消除。导航星天线相位中心偏差与变化、天线相位中心缠绕效应、相对论效应、地球自转、地球潮汐等采用PPP技术中模型改正的方法进行处理。
2.2 相对位置精度因子
基于GPS定位的位置/时间解的精度最终表示为几何因子和伪距误差因子之积。伪距误差因子指观测值上的等效距离误差。几何因子表示卫星和测站的相对几何布局[18]。
单点定位中,常采用最小二乘方法计算位置精度因子(position dilution precision,PDOP)评价单点定位中几何布局的好坏。对于星地差分GPS系统,本文提出通过相对位置精度因子(relative position dilution precision,RPDOP)来评价。
星地共视n颗(n>5)导航星时,可以组成n-1个伪距双差观测值。伪距双差观测线性化可得[19]:
V′=H′ΔX′+R′
(12)
式中:V′为伪距双差残差值;H′为双差伪距观测方程对位置参数求偏导数得到的雅克比矩阵;ΔX′为伪距双差状态量;R′为伪距双差观测总误差项。
伪距双差后已消除钟差量,H′可写为:
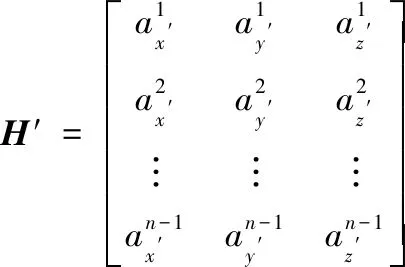
(13)
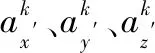
由H′可得:

(14)
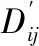
可见,矩阵H和矩阵G仅取决于可见卫星的个数及其相对于GPS接收机的几何分布。
实时星地差分GPS系统中,相对位置精度因子定义为:
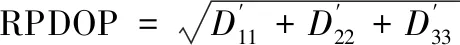
(15)
基于RPDOP公式,采用最小二乘法计算实时星地基线估计的相对位置精度因子。为了进行对比,引入单点定位的PDOP值。由于RPDOP和PDOP的值与观测卫星数目相关,所以计算时采用的伪距和载波相位观测数据为数据间隔1 s的低轨卫星和地面站的接收机数据,而非模拟器真值数据。
如图5所示,图5(a)显示了星地基线RPDOP值与低轨卫星PDOP值的比较,图5(b)显示了星地基线解算和单点定位中可用导航星数的比较。
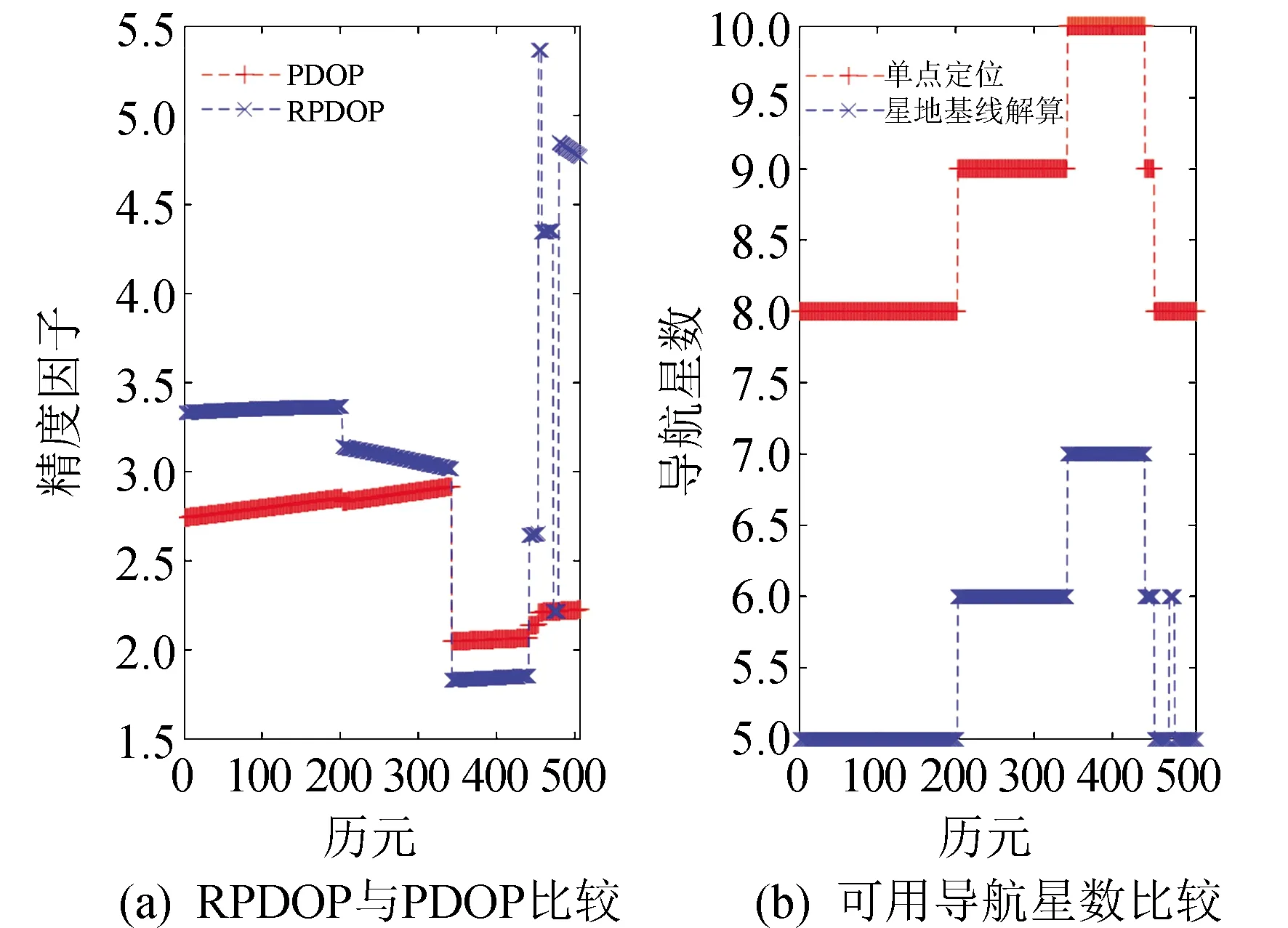
图5 星地基线的RPDOP与PDOPFig.5 RPDOP and PDOP of satellite-to-ground baseline
对比可知:1)RPDOP、PDOP值的大小均与可用导航星数成反比。2)星地基线的RPDOP值大于PDOP值。这是由于星地间基线较长,可视导航星数目减少所致。
进行多组测试和计算后可得,星地差分GPS系统性能评估中,星地基线的相对位置精度因子RPDOP可取为3.0。
2.3 实时星地基线估计精度预算
实时星地差分GPS系统采用伪距和载波相位的双差消电离层组合作为解算算法的观测模型。
接收机的伪距测量噪声一般为0.1~0.5 m,载波相位测量噪声一般为2 mm,消电离层组合将使伪距和载波相位测量噪声放大3倍,双差处理将使伪距和载波相位测量噪声放大2倍[20]。
因此,结合以上分析可得,采用双差消电离层组合观测模型,实时星地基线处理时,伪距测量误差的等效距离误差约0.640 3~3.008 3 m,载波相位的等效距离误差测量误差约为0.223 9 m。
星地基线估计精度的预算公式可记为:
Δd= RPDOP×σUERE
(16)
式中:Δd为星地基线估计精度预算;σUERE为星地双差观测值的等效距离误差。
结合RPDOP值和星地双差伪距、载波相位观测值的等效距离误差,可得实时星地基线估计精度的预算,如表1所示。
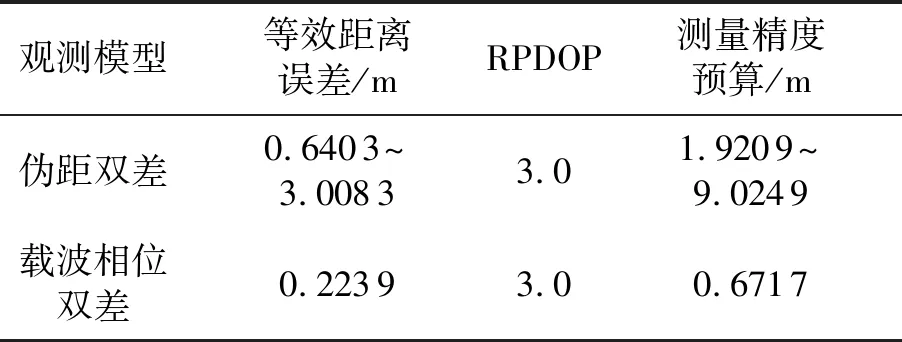
表1 实时星地基线估计精度预算
由此可得,星地差分GPS系统中,基于伪距的双差消电离层组合作为解算算法的观测模型,实时星地基线估计精度约为1.920 9~9.024 9 m,基于载波相位的双差消电离层组合作为解算算法的观测模型,实时星地基线估计精度可达0.671 7 m。
3 半实物仿真校验
为了验证实时星地基线估计算法的实际估计精度,本文基于SPIRENT GSS9000导航信号模拟器和星载GPS双频接收机开展半实物仿真研究,采用抗差自适应扩展卡尔曼滤波算法作为实时星地基线估计算法,并采用伪距、载波相位的双差消电离层组合作为实时星地基线估计算法的观测模型。仿真中,设置两颗低轨卫星位于不同轨道高度,两个地面站分别位于中国境内的不同位置,以验证不同星地基线长度下的实时星地基线估计精度。得到的基线估计精度作为比较基准,用于地基测控系统测量误差的实时标校。
3.1 仿真场景设置
半实物仿真平台包含两台GPS接收机,其中一台作为星载GPS接收机,另外一台作为地面测站接收机。根据表2中低轨卫星SPACEA和SPACEB轨道根数设置两颗低轨卫星的仿真场景,轨道高度分别为529.258 5 km、929.258 5 km。两个地面测控站A、B的位置坐标参数如表3所示。SPACEA-A和SPACEB-B构成两组星地基线,选取具体仿真弧段如表4所示。

表2 低轨卫星轨道根数设置

表3 地面站坐标设置(ECEF)

表4 两组实时星地基线
两组星地基线长度最大值为2 827 km,最小值为535.3 km。模拟器设置中,星载GPS接收机和地面GPS接收机观测上的电离层延迟分别采用基于电子浓度的电离层模型和Klobuchar电离层模型产生。对于地面接收机观测上的对流层延迟,模拟器采用STANAG模型[21]产生,而对于星载GPS接收机则关闭对流层。
3.2 实时星地基线估计误差仿真分析
本文采用实时星地基线估计算法对两组星地基线进行实时解算,以获取高精度的实时星地基线估计结果。仿真过程中,GPS数据采样间隔为1 s,截止仰角为5°。需要说明的是,考虑到滤波算法存在一定的收敛时间,初始阶段实时基线估计误差较大,以下统一取20 s以后的数据进行估计误差统计。
下面给出两组星地基线的实时星地基线的距离误差和速度误差,如图6所示。

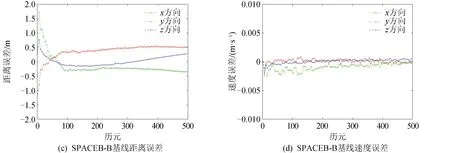
图6 两组实时星地基线误差Fig.6 Two sets of real-time satellite-to-ground baseline errors
两组实时星地基线估计精度结果如表5所示。由结果可知,当星地基线长度变化范围在500~3 000 km时,实时基线估计算法适用于不同轨道高度的低轨卫星的星地基线估计场景。实时星地基线解算的相对位置精度(三轴rms)在70 cm左右,与第2.3小节分析得到的实时星地基线估计精度理论分析值基本一致;实时星地基线解算的相对速度精度(三轴rms)在1 mm/s左右。

表5 实时星地基线估计精度(rms)
对比两组结果可知,低轨卫星的轨道高度与实时星地基线估计精度不存在必然的关系。这也验证了前文的分析,即实时星地基线估计精度仅与GPS观测误差和RPDOP相关。
3.3 地基测控系统测量误差标校仿真分析
将实时星地基线估计算法的解算结果作为比较基准,按照第1.2小节地基测控系统测量误差标校方法对包括设备时延、时间偏差、对流层延迟和电离层延迟的系统误差进行标定。仿真过程中,地基测控系统的测距、测速数据通过地基测控系统测量模型模拟产生。测距、测速相关误差项具体设置方案和误差量级如表6所示。

表6 测距、测速相关误差项具体设置方案和误差量级
将两组实时星地基线估计的相对位置矢量转化为星地距离测量值,相对速度转化为径向速度值,作为地基测控系统测量数据的比较标准。然后采用加权最小二乘估计方法求解测距误差模型系数。由于测距、测速系统误差的标定精度除了受GPS测量精度的影响,还受测距、测速自身随机误差的影响,故仿真过程中针对每组星地基线随机产生1 000组随机误差,对测距和测速误差标定结果进行评定。
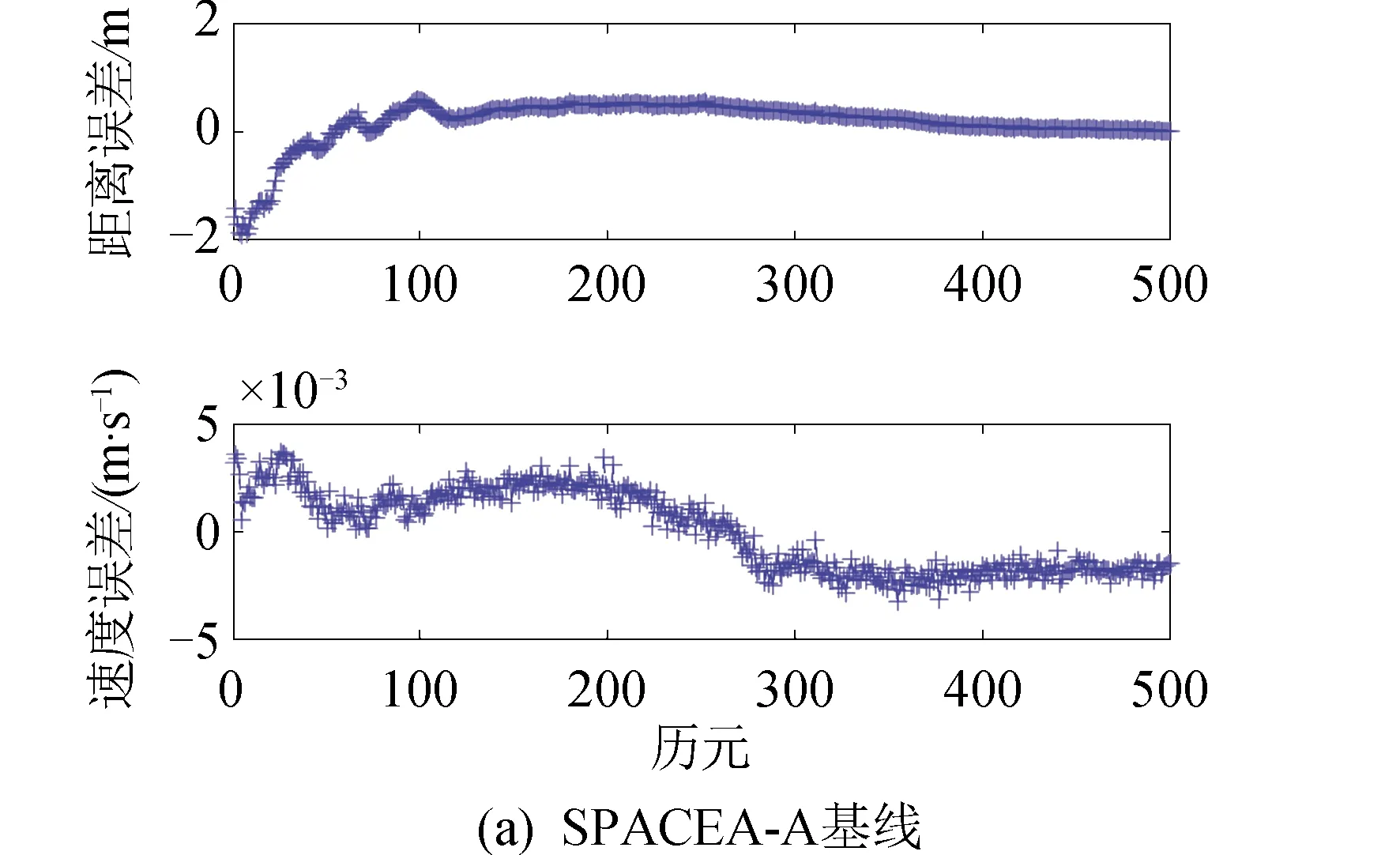

图7 两组实时星地基线在各自视线方向上的误差Fig.7 Two sets of real-time satellite-to-ground baseline errors in their respective line of sight directions
图7表示两组实时星地基线在各自视线方向上的测距、测速误差。其中,视线方向上的距离误差由星地基线的相对位置误差在视线方向上的投影得到,视线方向上的速度误差由星地基线的相对速度误差在视线方向上的投影得到。两组测距、测速误差标校的仿真结果如图8和图9所示。每组结果的左图和右图分别为测距、测速的实时标校结果。其中,每个图的上图表示测距、测速总误差与经过实时标校后得到的标定的测距、测速系统误差的对比,其中测距、测速总误差由地基测控系统测量误差模型产生,包含系统误差和随机误差;中图表示测距、测速随机误差与测距、测速残差的对比,其中测距、测速残差由测距、测速总误差与标定的测距、测速系统误差作差得到;下图表示标校后测距、测速的系统误差的残差,由测距、测速残差与测距、测速的随机误差作差得到,该值是标校精度的直接体现,反映标校性能的好坏。
实时标校后测距和测速系统误差残差的统计结果如表7所示。由表7可知,对不同轨道高度的低轨卫星和不同地面站构成的星地基线进行实时解算,当星地基线变化范围在500~3 000 km范围内时,两组实时星地基线估计结果在视线方向上的距离误差为50 cm左右,视线方向上的速度误差为3 mm/s以下。实时标校后,测距的系统误差的残差降低到40 cm左右,测速的系统误差的残差降低到1 cm/s以下。
同样,对比不同轨道高度的低轨卫星的测距、测速的系统误差的实时标校结果可知,低轨卫星的轨道高度对测距、测速系统误差的实时标校无明显影响。
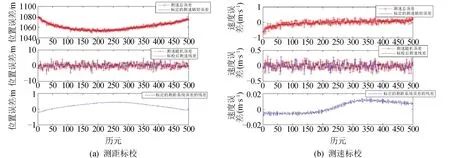
图8 星地基线SPACEA-A的测距和测速误差实时标校Fig.8 Real time calibration of ranging and velocity measurement errors of SPACEA-A
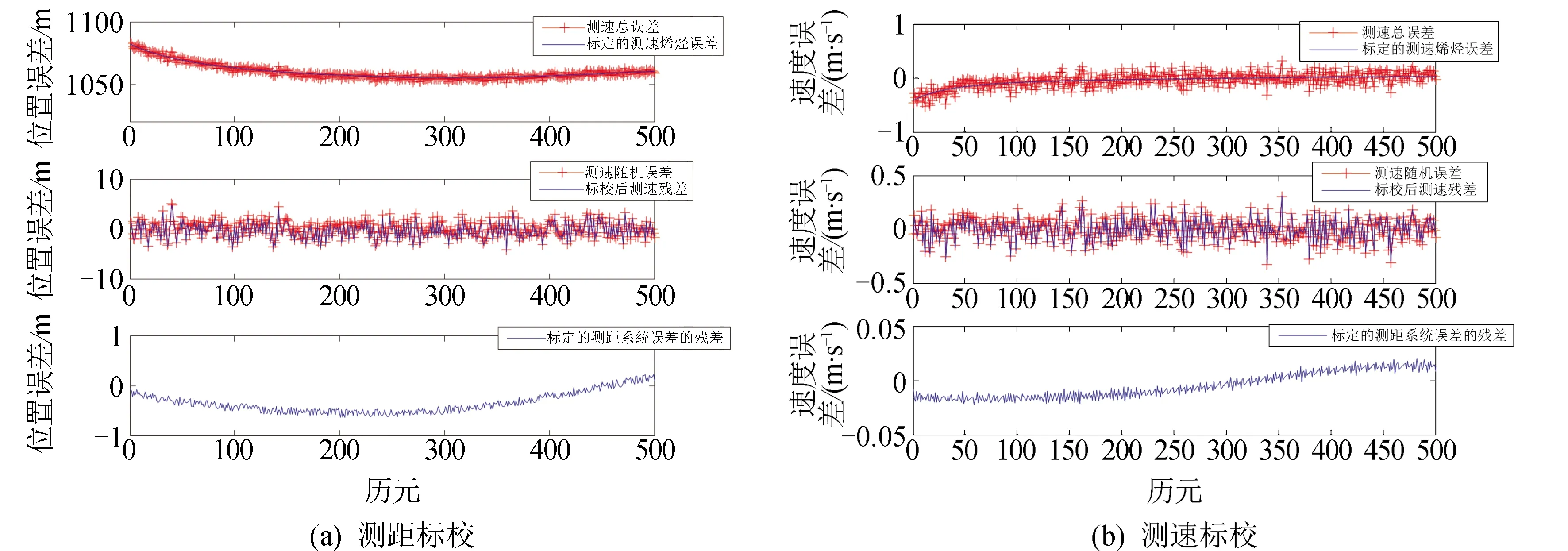
图9 星地基线SPACEB-B的测距和测速误差实时标校Fig.9 Real time calibration of ranging and velocity measurement errors of SPACEB-B

表7 实时标校后测距/测速的系统误差的残差(rms)
4 结束语
本文提出了一种利用星地差分GPS的地基测控系统测量误差实时标校方法,具有以下优点:
1)半实物仿真表明,利用星地差分GPS的方法对地基测控系统进行实时标校,可使测控和测速的系统误差残差分别降到了40 cm左右和1 cm/s以下,大大超出了传统标校方法可提供的标校精度。
2)该方法是一种对地基测控系统的实时标校方法。当地基测控系统对标校实时性有较高要求时,事后标校的研究方法显然无法满足要求,而该方法具有巨大的优势。
3)本文针对星地间长基线和高动态的环境,提出了相对位置精度因子的概念,并给出了实时基线估计精度预算。所以该方法具有充分的理论分析,可为之后的工程实践提供理论支撑。
该方法作为一种对地基测控系统实时标校的应用方案而提出。仅通过理论分析和导航信号模拟器的仿真校验,并未采用实测数据验证。随着工作的有序开展,后续会采用浙江大学皮星三号(ZDPS-3)卫星作为标校卫星平台,通过实测数据开展精度验证工作,具有更加深远的意义。
