北斗GEO卫星CEI相时延解算方法研究

陈少伍，王静温，黄磊，徐得珍

1. 北京跟踪与通信技术研究所，北京 100094 2. 北京遥测技术研究所，北京 100094

通过相距10～100 km的2个测站之间的光纤进行频率和信息的传递，以实现对2个测站接收信号延迟的精确测量，进而可以实时或准实时地确定目标相对两站间基线矢量的精确角位置。该技术在地球静止卫星相对定位、近地空间交会对接航天器相对状态监视中均具有重要作用[1-3]。此外，该技术在深空航天器导航中也具有重要作用[4-7]。

连线端站干涉测量(connected element interferometry，CEI)技术通过光纤把一个测站时间和频率信息传送至其他测站，消除了传统甚长基线干涉测量(very long baseline interferometry，VLBI)技术中独立本振频率稳定性和时间同步的影响。由于测站距离近，航天器信号至测站传播路径上电离层、大气效应具有很强的相干性，通过差分能够很好地消除。美国国家航空航天局(NASA)开展了大量研究及试验，并取得了很好的效果，日本也在20世纪90年代开展相关试验。国内，北京航天飞行控制中心、信息工程大学及装备学院等均开展了相应仿真和实测分析研究，这些研究为该技术奠定了基础[8-12]。目前，研究方向主要为传统差分单向测距(differentia one-way ranging，DOR)或宽带信号CEI测量精度仿真[9-13]、CEI技术定轨精度分析[14-15]。采用传统干涉测量方式，通过交替观测射电源和航天器，消除共性误差，获取时延观测量[13]。

目前，近地航天器无下行DOR音信号，只能发送下行测距和遥测信号，基于DOR音和宽带信号的传统处理分析方法不再适用。本文在此基础上开展研究，利用佳木斯深空站构建CEI系统，对北斗地球静止轨道(geosynchronous earth orbit，GEO)卫星进行观测，利用下行相干测距信号解算相时延，并根据GEO精密轨道对CEI群时延(group delay，GD)和相时延(phase delay，PD)残差进行评估。

1 连线端站干涉测量系统

首先构建连线端站干涉测量系统。选取佳木斯深空站作为主站，选取距离主站50 km的另一个测站作为副站，两者之间通过光纤设备进行连接，构建连线端站干涉测量系统如图 1所示。佳木斯深空站配备高稳氢钟，同时站内配备有全球定位系统 (global position system，GPS)接收机，站内时频分系统利用氢钟频率、GPS接收机数据生成时间信号，通过光纤将时间和频率信息传送至副站。

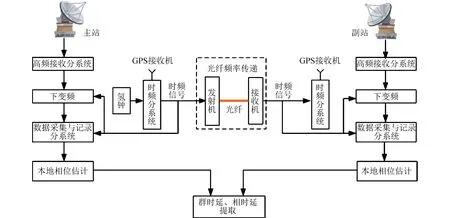
图1 CEI系统基本原理框图Fig. 1 The schematic of the CEI system

航天器信号经过空间传播后，分别达到地面主站和副站。信号经高频接收系统接收、下变频处理，送入数据采集和记录分系统。通过本地相位估计提取主站和副站信号的相位，最后相位送至处理中心，计算站间相位差并解算群时延和相时延。在下变频处理以及数据采集记录过程中均采用本地时频分系统产生的时间和频率信号。由于两个测站通过光纤实现了时间和频率的同步，因此下变频处理以及数据采集记录均是同一频率源。

传统VLBI中均采用了DOR音信号作为下行信标。通常，近地航天器下行仅测距音及遥测信号，无DOR音信号。遥测信号采用普通晶振，频率稳定度较差，由此将引入时延测量误差。

为此，本文提出了一种新的测量方法，即相干测距模式下CEI测量。测量原理如图 2所示，副站对航天器进行测控过程中，副站发送上行测距信号，器上应答机接收信号并进行相干转发，信号经过接收系统和下变频处理后，由数据采集与记录设备进行开环记录。

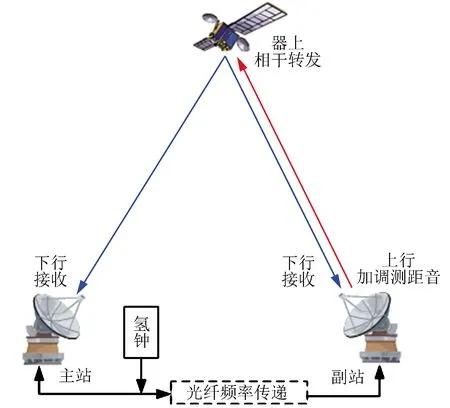
图2 相干测距模式下CEI系统测量示意Fig. 2 The sketch map of CEI in coherent ranging mode

主站氢钟频率是主站频率参考，同时通过光纤时频传递系统传递至副站，主站、副站均采用氢钟频率作为频率参考。副站对航天器进行上行测控，上行载波和测距信号由副站频率源生成。航天器相干测距模式下，下行信号与上行相干。因此下行信号传播、主站和副站地面采集与记录设备均以氢钟频率为参考。

2 CEI误差分析

干涉测量中主要误差有：对流层、电离层等引入的误差，测站间时钟误差，测站位置误差，设备时延误差等[12-13,16]。相对于VLBI系统，CEI系统对流层误差、电离层误差等共性误差可很好地消除，以下针对佳木斯深空站CEI系统和北斗GEO卫星进行具体分析。

2.1 对流层时延误差

对流层时延可表示为:

τtrop=τZHD×mh+τZWD×mw

(1)

式中：τZHD、τZWD分别为对流层干燥大气、水蒸气时延;mh、mw为对应的Neill映射函数，通常两者非常近似，因此τtrop=τZTD×mh，τZTD为天顶方向总大气时延。

在CEI测量中两个测站距离非常近，观测目标为地球静止轨道卫星(距离测站约3.6×104km)，两者俯仰角之差小于0.5°，信号到达两个测站的空间传播路径相近，误差相关性很强，站间差分消除共有误差影响。假设τZTD为2 m，利用佳木斯深空站对北斗G6卫星进行观测时，俯仰角约30°，此时大气时延误差为0.1 ns。

2.2 电离层时延误差

单个测站电离层时延可表示为：

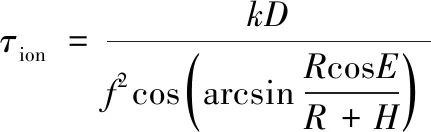
(2)

式中：k为常数，k=1.34×10-7;f为电磁波的频率；D为信号传播路径上的总电子含量；R为地球半径；H为电离层高度；E为俯仰角。

CEI测量系统电离层时延误差为该基线上两个测站的电离层时延之差，即：

Δτion=τion1-τion2

(3)

式中：τion1、τion2分别为信号传播到主站和副站的电离层时延。

北斗GEO卫星下行测控信号为S频段，假设D为50 TECU(1 TECU=1016个电子/m2，D实际值为10～20 TECU) ，两站俯仰角之差小于0.5°，利用佳木斯深空站对北斗G6卫星进行观测时，电离层时延误差为0.008 ns。

2.3 设备时延误差

设备时延误差主要为信号经接收机后，信号在地面设备传输过程中引入的时延误差。主要包括：电缆时延、下变频设备时延、采集设备通道时延、信号处理硬件时延等。此外由于温度、湿度等环境变化，导致仪器设备时延抖动。

2.4 时间同步误差

CEI系统采用光纤传输时间和频率信息，站间距较短时间同步精度较高。光纤传递法可以实现0.1 ns或更低的时间同步精度。

时间同步引入的系统误差可以表示为：

στ1=ετ

(4)

式中：ετ为站间时间同步误差。目前站间时间同步误差为0.1 ns，其引入的时延系统差为0.1 ns。

时间同步引入的随机误差可表示为：

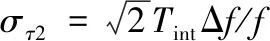
(5)

式中：Δf/f为阿伦方差；Tint为积分时间。目前氢钟的阿伦方差假设为10-14/s，每次观测的积分时间为1 s，时间同步引起随机差为1.4×10-4ps。

2.5 热噪声误差

利用佳木斯CEI系统对北斗GEO观测时，整个链路预算情况参如表 1所示。根据表1可知，载波信号站间相位差的随机误差为0.002 14°；主音信号站间相位差的随机误差为0.003 98°。因此，±100 kHz测距信号群时延随机误差为5.5 ns，载波相时延随机误差为0.27 ps。

3 相时延解算与试验结果分析

3.1 试验情况

利用佳木斯深空站CEI系统进行2次试验。第1次试验为第1天8:40～10:50，第2次试验为第2天8:50～11:40。试验首先对北斗G6卫星进行长时间观测，再进行间断观测。观测过程中，副站对北斗G6卫星发送上行信号，深空站和副站同时采集和记录下行信号。

北斗G6卫星下行信号频谱如图 3所示，主要包括载波和±100 kHz测距音信号3个频点。根据采集记录的北斗G6卫星下行数据，提取载波和±100 kHz测距音相位，获得站间相位差记

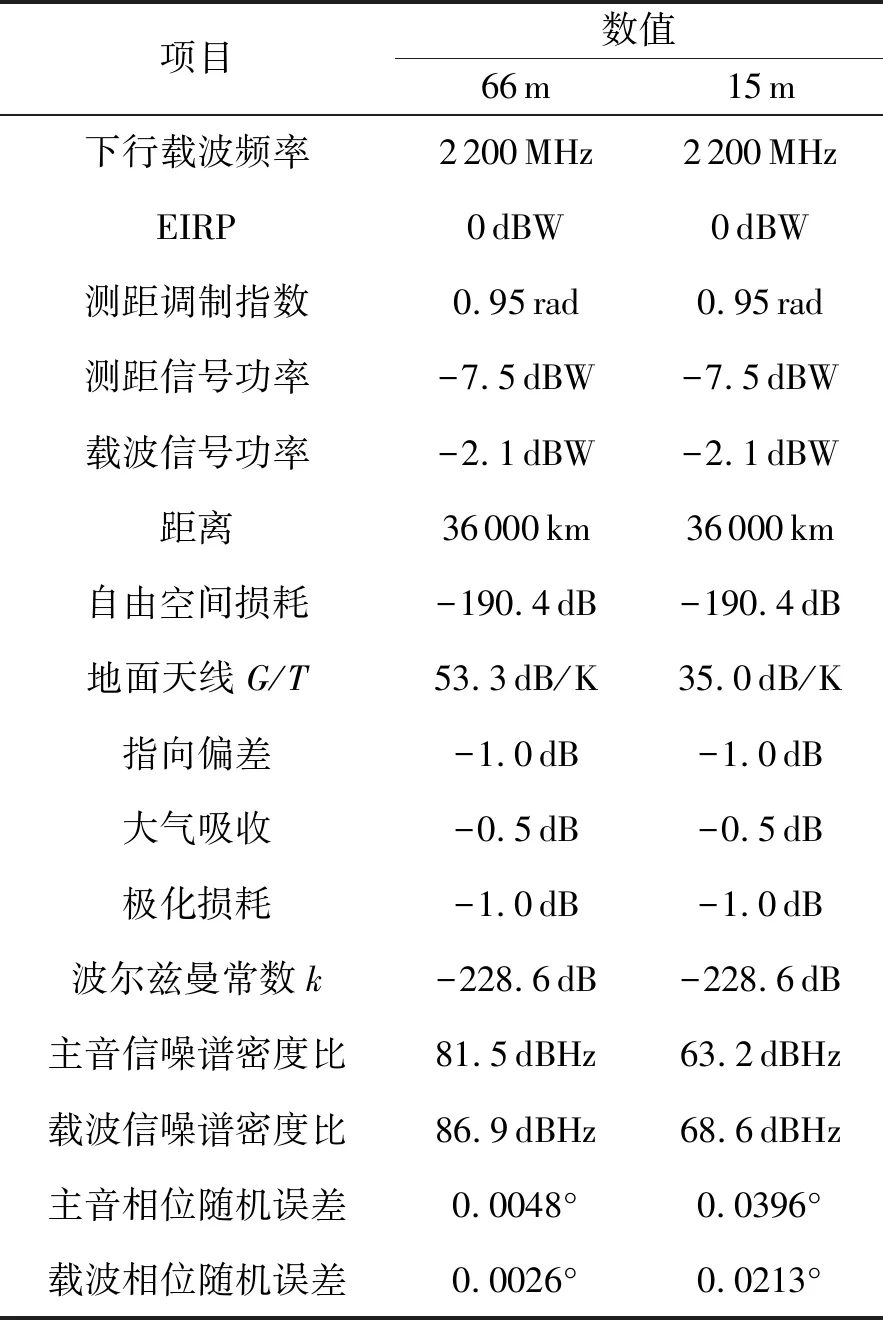
表1 地球静止轨道卫星链路分析及相位估计随机误差

为φi(i=-1，0，1，分别表示-100 kHz测距音、载波和+100 kHz测距音)。3个信号的站间相位差如图 4所示。根据图 4可知在连续观测弧段内北斗G6卫星站间相位差连续。

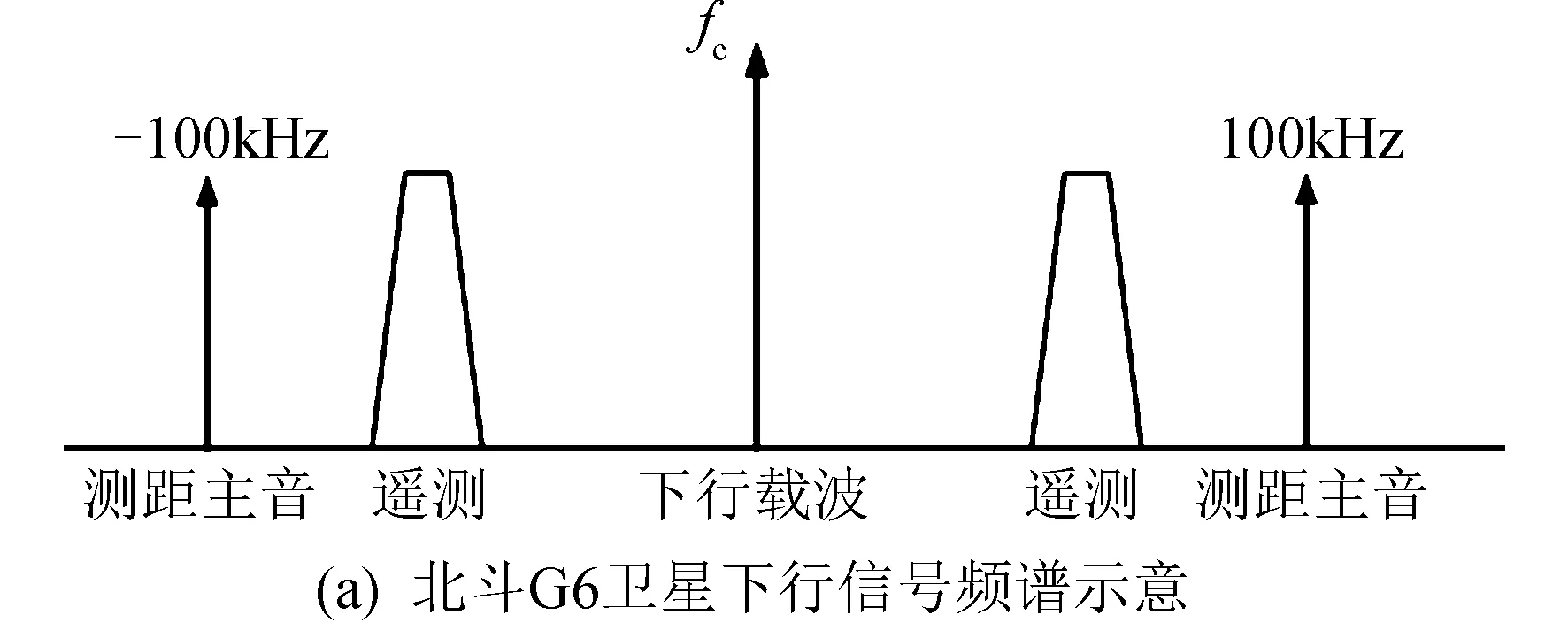
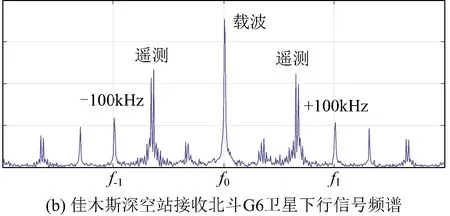
图3 北斗G6卫星下行信号频谱Fig. 3 The spectrum of BDS G6 downlink signal

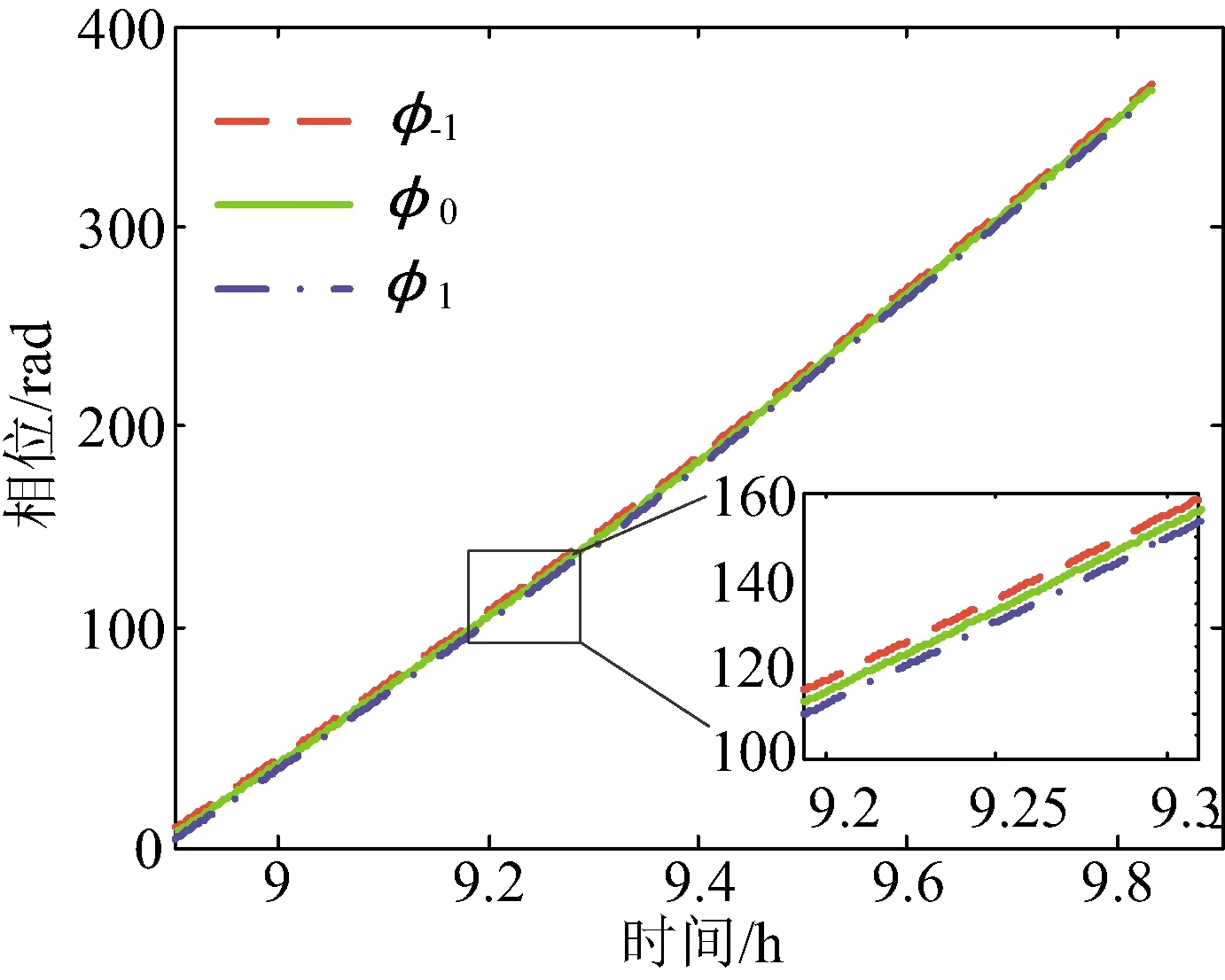
图4 北斗G6卫星3个频点的相位差时间变化曲线Fig. 4 The phase difference of the carrier and ranging signals of BDS G6 satellite

3.2 群时延解算

站间相位差φi可以表示为：

φi=2π(fiτgeo+fiτels-kΔD/fi+Ni)+σi

(6)

式中：fi为信号频率；τgeo为几何时延；ΔD为信号路径上电子密度含量之差；τels为对流层、仪器设备和钟差引入的时延误差之和；Ni为相位整周模糊；k为常数,k=1.34×10-7；σi为相位噪声。

测距音最大带宽为200 kHz，群时延一个整周模糊为5 000 ns。目前北斗GEO卫星导航电文位置误差为5 m，对应50 km基线时延误差为20 ps。根据前文分析，电离层引入的时延误差为8 ps，相时延随机误差在10-2ps量级。上述误差远小于5 000 ns，因此，测距音和载波之间相位不存在整周模糊(N-1=N0=N1)。根据多频点群时延推导法[17-18]，群时可以表示为：

ΔτGD=(φ1-φ-1)/2π(f1-f-1)

(7)

3.3 相时延解算

为提高测量精度，本文在群时延解算的基础上，进行进一步研究，提出了相干状态下北斗GEO卫星高精度CEI相时延推导求解方法。

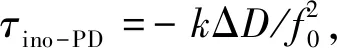
佳木斯CEI系统对北斗G6卫星进行观测时，两站俯仰角几乎相同。载波以及±100 kHz测距音信号频率非常接近，群时延和相时延中电离层引入误差约8 ps，远小于S频段一个整周时延(0.45 ns)，因此利用群时延结果可以对相时延进行约束。为此本文提出了适用于CEI系统的群时延辅助求解相时延方法。基本思路如下：

1)采用多频点群时延推导法求解群时延ΔτGD，对连续观测弧段内的群时延结果进行预处理，剔除野值；

2)对拟合残差进行积分处理，获得积分时间60 s时群时延结果。

北斗GEO卫星相对地面站运动速度在10 m/s量级，两次观测时刻时延变化约40 ps，对应S频段相位变化约0.16π，因此连续观测弧段内站间相位差分连续。根据上述原理，获得连续站间相位差。对弧段内连续站间相位进行整周补偿，不同整周模糊时相时延和群时延结果见图 5上图，根据上述结果计算不同的整周模糊对应的相时延和群时延之差的标准差见图 5下图。标准差最小时对应该弧段整周模糊N0。整周模糊补偿，解算相时延ΔτPD可以表示为:

ΔτPD=(φ0+2πN0)/(2πf0)

(8)

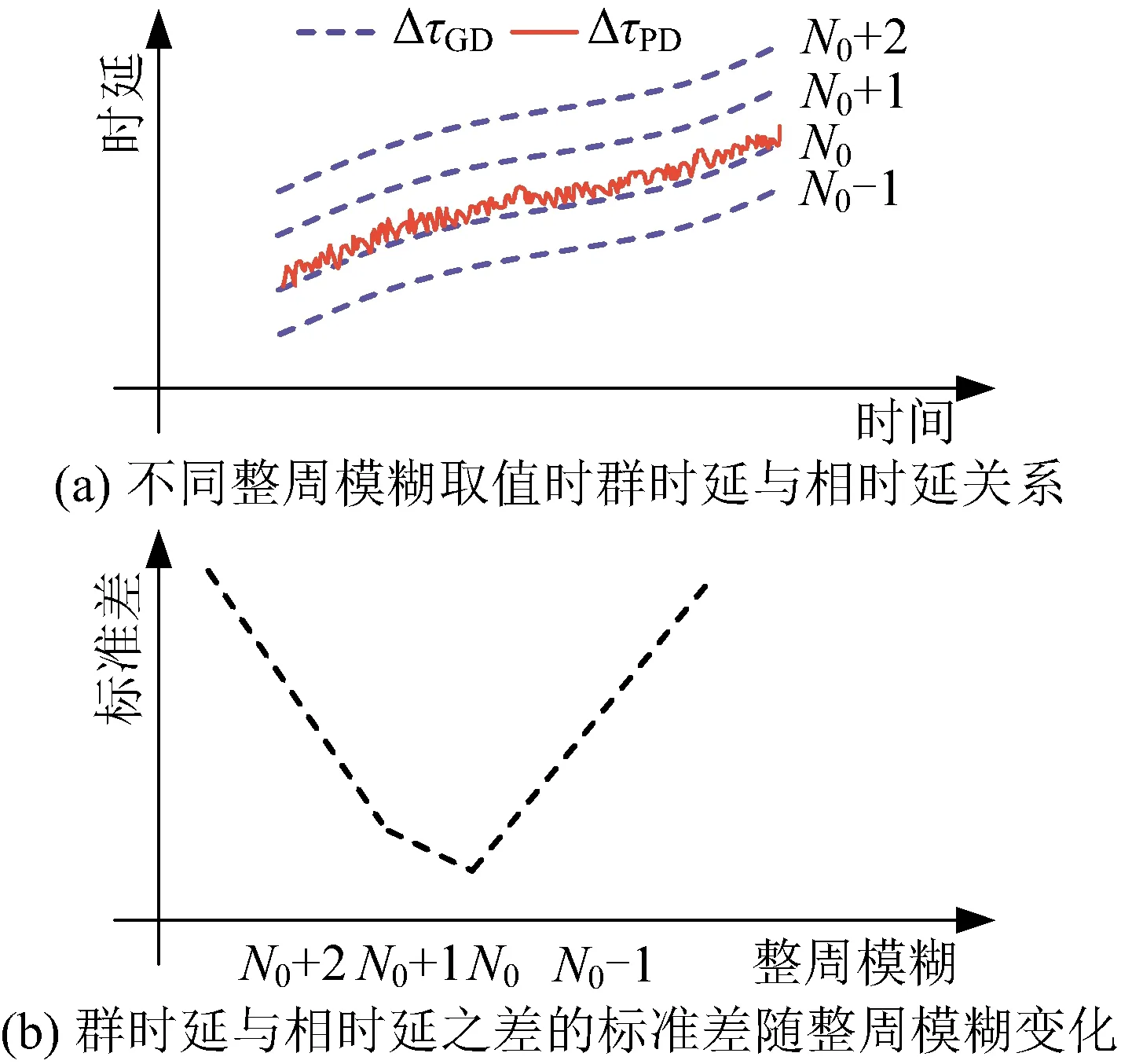
图5 群时延辅助求解整周模糊示意Fig. 5 The schematic of resolving cycle ambiguity using group delay

3.4 结果分析

根据站间差分相位数据，提取北斗G6卫星群时延和相时延结果如图 6所示。根据图 6可知，两者随时间变化趋势一致，群时延结果曲线存在较大的随机误差，相时延随机误差远小于群时延随机误差。

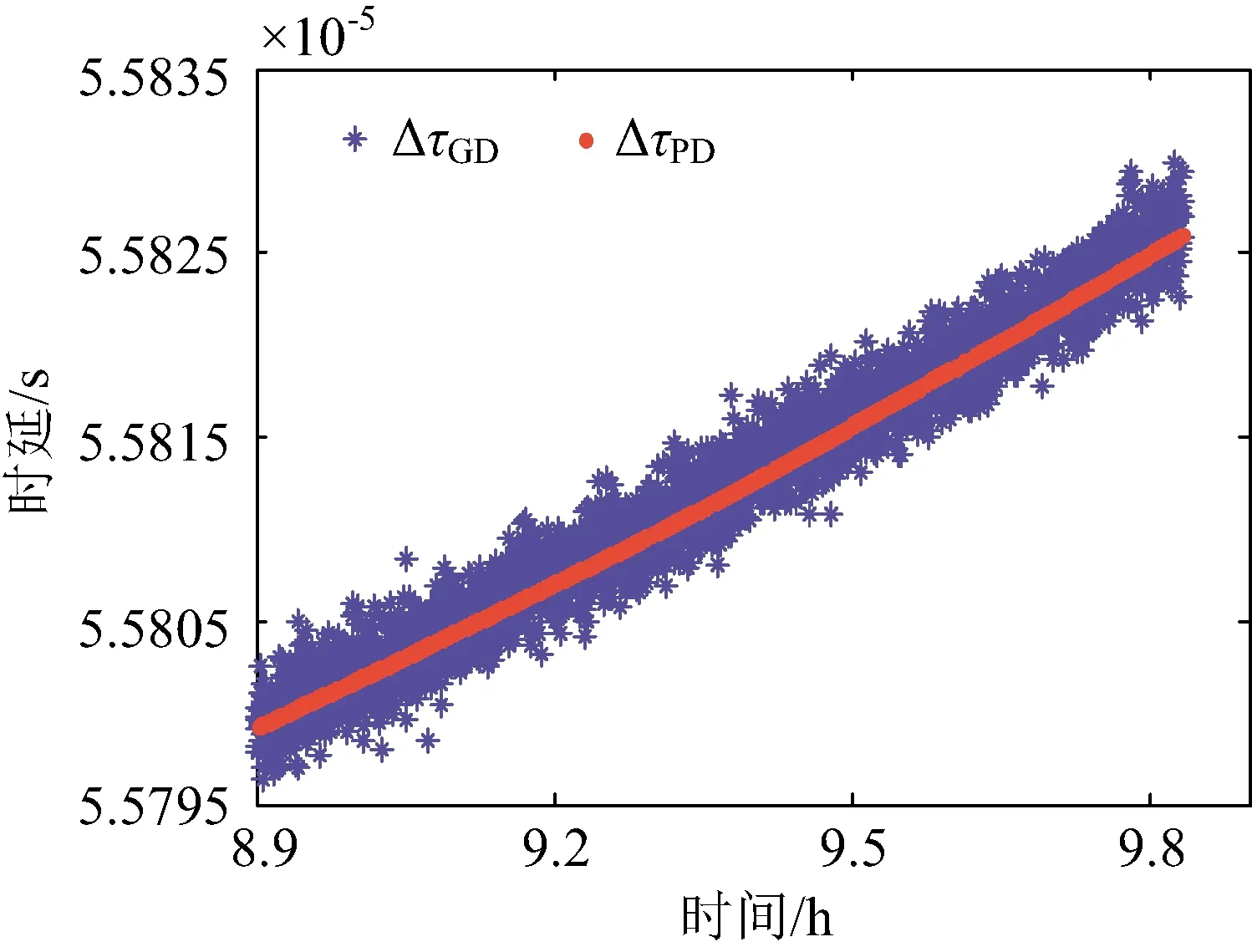
图6 北斗G6卫星CEI时延值随时间变化曲线Fig. 6 The CEI delay of BDS G6 satellite

首先对北斗G6卫星进行1 h10 min长时间观测，利用群时延和相时延标定CEI系统误差分别为-241.05 ns、-241.31 ns。在此基础上对后续4个弧段的测量结果进行修正，根据北斗G6卫星精密星历获得时延观测量残差，结果如图 7所示。根据图 7(a)可知，群时延和相时延残差均在零值附近变化，群时延残差在±4 ns范围内变化，根据图 7(b)相时延残差结果可知，相时延残差在±100 ps范围内变化。群时延残差精度较差，相时延精度显著提高。

为了使结果不失一般性，对两次试验的群时延和相时延残差进行统计，统计结果如表2所示。根据表2可知，群时延和相时延残差系统差分别为0.48 ns和0.08 ns，相时延解算整周模糊，系统误差显著减少。群时延和相时延残差标准差(3σ)分别为4.2 ns、0.13 ns，相时延残差标准显著减少。

以下对上述结果进行进一步分析。目前北斗G6卫星导航电文位置误差引入时延误差为20 ps，电离层和对流层引入时延误差在10 ps量级。根据第2.5小节中链路预算结果，测量设备热噪声引入群时延的随机误差为5.5 ns，远大于其他误差影响，群时延误差中主要表现为随机误差。该随机误差与实际观测获得的时延随机误差相当。根据链路预算结果，相时延机误差为0.3 ps，根据图7(b)可知，相时延残差存在约100 ps误差，存在明显的趋势项。这些趋势项主要反映北斗G6卫星残余位置误差、电离层及对流层引入误差。

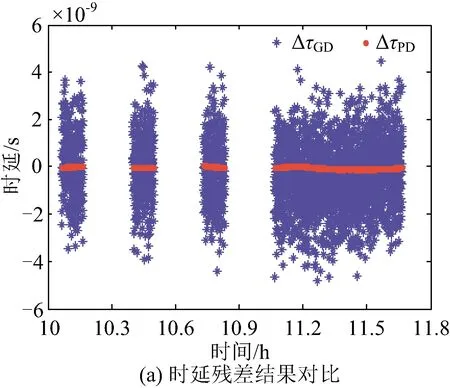
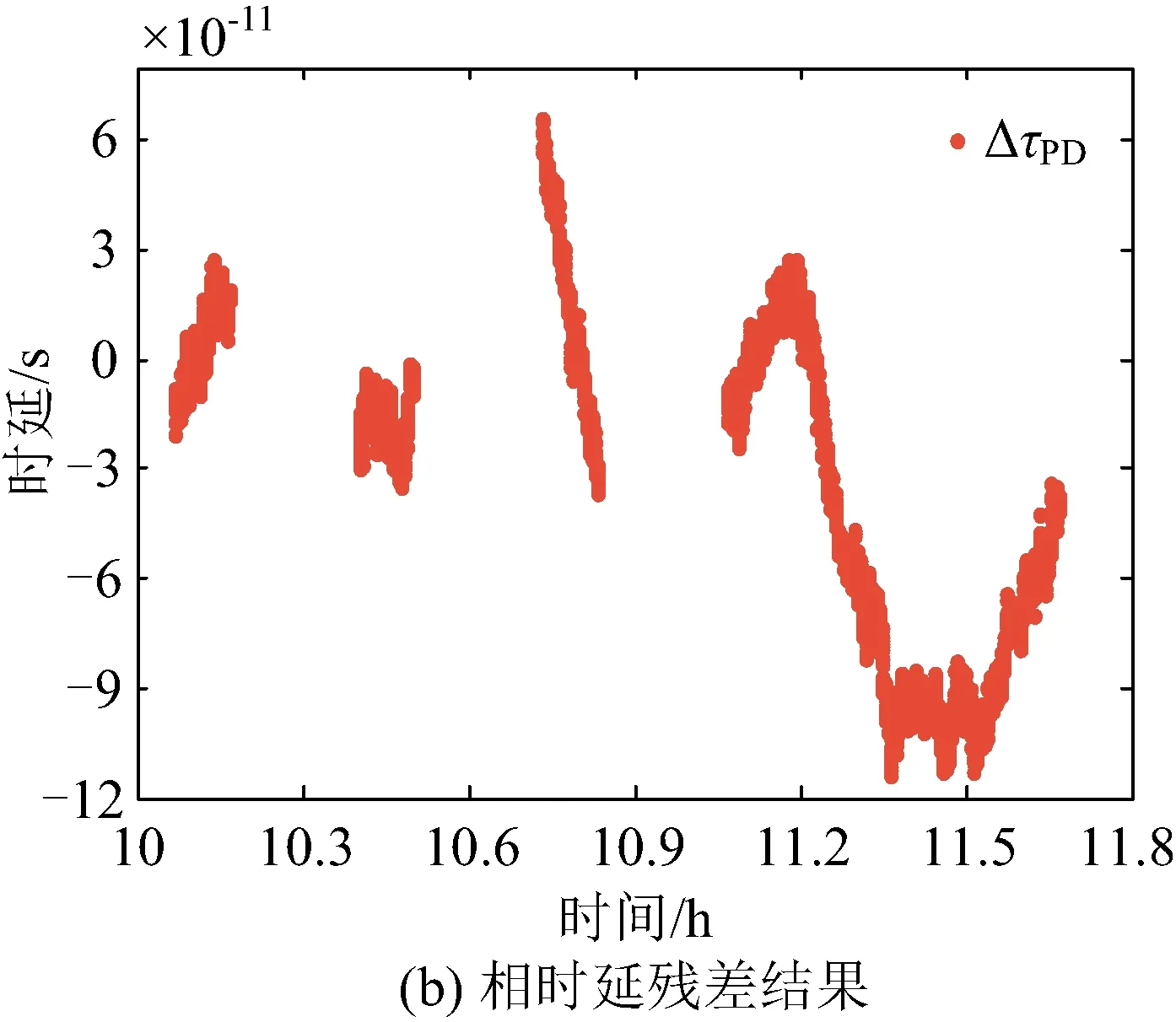
图7 北斗G6卫星CEI系统时延残差结果Fig. 7 CEI delay residual of BDS G6 satellite

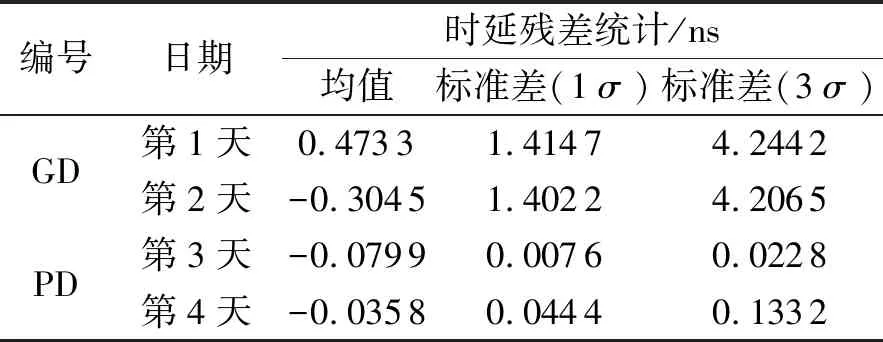
表2 CEI时延残差统计结果

4 结束语

本文介绍了基于光纤时间频率传递技术构建的CEI测量系统，提出了利用相干测距音和载波信号作为信号源的干涉测量模式，定量分析CEI测量的主要误差因素。根据CEI试验记录的数据，获得了站间相位差，解算群时延和相时延。试验结果表明，利用相干测距信号成功获取相时延，相时延残差均值为0.08 ns，标准差可达到100 ps量级。

本文提出的方法主要技术优点为：

1)基于现有测音测距技术体制，利用测距信号即可实现，不需要DOR音及宽带信号；

2)利用光纤时频传递技术并配备采集记录设备即可实现测量；

3)在现有条件下测量精度可达100 ps量级。

该研究对共位地球静止轨道卫星高精度的差分相时延测量、精密相对定位以及月球及深空探测器高精度测轨定位均具有重要参考意义。