小卫星侦察星座性能评估研究

王浩，张占月，张海涛，姜平

航天工程大学，北京 101400

随着小卫星行业发展热潮不断兴起，以小卫星为主体的星座建设成为航天领域关注的焦点。小卫星星座具有成本低、高空间分辨率和高时间分辨率的特点，可用于替代高度集成和寿命长的大卫星[1-3]，小卫星组网侦查是遂行侦察任务的有效手段。星座性能决定了星座是否能圆满完成侦察任务，对侦察小卫星星座性能评估指标进行研究，有助于提高小卫星侦察星座的建设和性能评估。

众多学者对侦察星座的性能指标及评估方法进行了研究。文献[4-5]针对星座覆盖性能评估指标进行了研究，按照区域重要程度不同，提出加权覆盖特性指标，如加权覆盖率、加权最大重访时间等。文献[6]针对侦察星座的探测能力和覆盖能力问题，构建了探测能力指标计算模型，并探究了探测能力和覆盖能力之间关系。文献[7-9]针对区域目标覆盖性能指标计算效率低的问题，提出了基于系统抽样理论的高效抽样网格点法。文献[10]对当前各国成本估计模型进行调查，并对参数估计法进行改进，提高了星座成本估计的准确度和保真度。文献[11]对现有三种小卫星星座成本估计模型进行综述，重点分析了三个成本估计模型的优缺点和适用范围。文献[12]提出了基于性能的星座成本估计模型，通过分析固定分辨率和覆盖要求下成本与轨道高度、成本与分辨率以及成本与覆盖之间关系，来量化成本与性能之间的关系。文献[13]将弹性定义为避免、承受、适应干扰和未知破坏事件的能力，以及遭受干扰和未知破坏事件后的恢复能力。文献[14]总结了影响太空弹性体系架构的四个关键因素，并指出小卫星星座是实现高弹性、低成本太空弹性体系架构的有效方案，但并未给出弹性能力的度量方法。

目前对侦察星座性能评估主要考虑覆盖和成本两类指标，也有文献研究侦察星座的弹性能力，但三者综合考虑研究的情况较少，这使得传统星座抗毁性差，难以满足侦察星座高时效、快响应、高弹性的需求。此外，对于批量制造的小卫星而言，卫星成本大幅降低，足以支撑弹性星座建设。本文对侦察小卫星星座的性能评估指标进行分析研究，主要考虑覆盖、成本和弹性三个方面。

1 覆盖能力及度量方法

对于侦察任务而言，覆盖能力是侦察星座最重要的性能，星座能否对目标覆盖是任务完成的先决条件。覆盖性能指标众多，可根据指标状态属性划分为空间域、时间域和质量域指标[15]，如图1所示。反映星座对目标空间域覆盖能力的指标有覆盖百分比、覆盖面积和覆盖重数等；反映星座对目标时间域覆盖能力的指标有重访时间、覆盖间隙、平均响应时间和覆盖时长等；反映星座对目标覆盖质量的指标有空间分辨率和瞬时覆盖面积[16]。

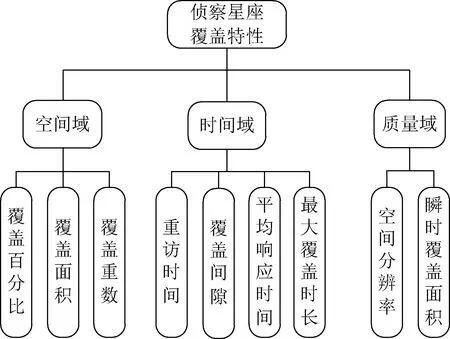
图1 覆盖性能指标Fig.1 Coverage performance indexes

传统覆盖计算方法中只考虑卫星对目标能否覆盖，并未考虑卫星存储容量对覆盖能力的影响。卫星实际工作过程中，卫星本身具有一定量的额定存储容量，当存储容量超过额定存储容量时，卫星将无法继续提供对地覆盖。相比于大卫星而言，小卫星本体存储容量更低，在轨持续工作时间更短。因此对小卫星的覆盖能力进行研究时，必须考虑卫星存储容量对卫星覆盖能力的影响。

假设卫星开始覆盖目标区域时即开机工作，离开目标区域时关机。卫星工作时产生数据速率为E，总存储容量为M，若不考虑数据下传，最多工作时长为M/E。卫星数据下传方式分为通过中继卫星下传和直接对地下传，通过中继卫星可一直进行传输，当卫星对地面数据接收站可见时，则直接对地传输，不通过中继卫星下传。卫星通过中继卫星进行数据下传速率为K，对地传输速率为L，目标区域在星地链路范围内的比例为μ，则可计算出卫星侦察最大时长tM，如式(1)所示，只有当卫星对目标区域单次覆盖时长不超过卫星侦察最大时长，卫星可以继续工作。

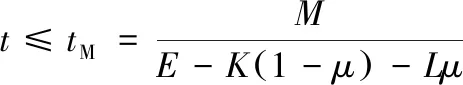
(1)

式中：t为卫星对目标区域单次覆盖时长。

如图2所示，卫星S运行于轨道高度为h的圆形轨道上，O为地心，T为目标点。通过卫星TLE数据和Sgp4轨道预报模型计算可得卫星在J2000坐标系下的坐标，将卫星在J2000坐标系下的坐标转换为地球固定坐标系下的坐标S(t)，如式(2)所示。为了简化模型，暂不考虑岁差、章动、极移对轨道的影响。

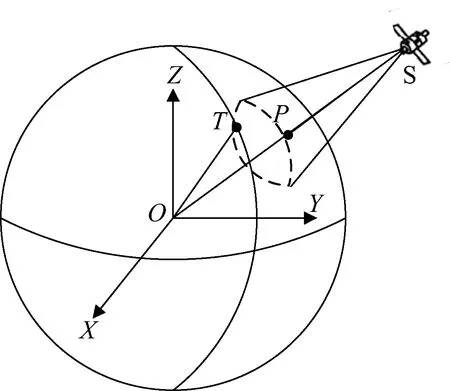
图2 卫星对地覆盖Fig.2 Satellite coverage

式中:[sX(t),sY(t),sZ(t)]T为当前时刻卫星在地球固定坐标系下的坐标矩阵；[uX(t),uY(t),uZ(t)]T为当前时刻卫星在J2000坐标系下的坐标矩阵；θ(t)为当前时刻下的格林尼治恒星时角；G(θ(t))为J2000坐标系到地球固定坐标系下的坐标转化矩阵。

假设地球为标准圆球体，目标在地球上的经纬度坐标(λ,φ)，目标点在地球固定坐标系的坐标为Ttar。载荷视场为锥形，视场半角为β，卫星最大侧摆角为±α，假定目标处于卫星通过侧摆达到的最大覆盖范围之内即可以被卫星侦察到，根据几何模型和卫星侦察最大时长，当目标能够被卫星覆盖时，需满足式(1)和式(3)。

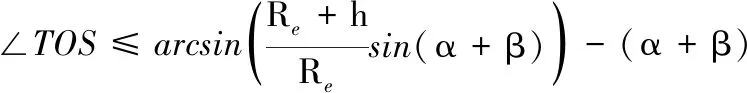
(3)

式中：Re为地球半径；∠TOS为目标和卫星与地心连线的夹角。

目前对网格点法的研究集中于改善网格点法计算速度慢的缺点，很少考虑卫星本体及环境约束对覆盖性能的影响，如存储容量、天气等。本文对传统网格点进行改进，提出考虑存储容量的覆盖指标计算方法。步骤分为五步，一是将区域目标按一定规则划分为多个网格，目前常用的网格划分方法为等经纬度法和等面积法[8]；二是计算星座中每颗卫星对每个网格点(以每个网格的中心作为网格点)的覆盖情况；三是合并重叠时间段，得到每颗卫星对目标区域的覆盖情况，并根据存储容量对覆盖时间片段进行截取，去除无效片段；四是根据处理后的卫星对目标区域的覆盖情况，确定卫星对目标区域内所有网格点的覆盖状态；五是统计时间域和空间域上星座对目标区域的覆盖情况，计算覆盖性能指标。下面以覆盖百分比和最大重访时间为例，通过改进的网格点法计算相应值，其他时间域和空间域覆盖指标计算与之类似。

根据式(3)确定仿真时段内每颗卫星对每个网格点的覆盖时段，同一时间轴下合并重叠时间段，得到单颗卫星对目标区域的覆盖情况，如图3(a)所示。考虑到卫星存储容量对卫星状态的影响，对卫星的每个覆盖时间片段进行判断，当覆盖时间片段大于卫星侦察最大时长，说明卫星在此时段内存储容量已超过卫星本身总存储容量，故需对超过最大时长以后的时间片段进行截取，图3(a)中阴影部分表示截取的覆盖时间片段。当覆盖片段小于卫星侦察最大时长时，说明卫星在此时段内存储容量未超过卫星总存储容量。经过片段截取后的卫星对目标区域的覆盖情况如图3(b)所示。卫星i(文中i，j，k均指对应的编号值)的状态函数可用F(i,t)表示，t时刻卫星i对目标区域覆盖取1，否则取0，如式(4)和式(5)所示。

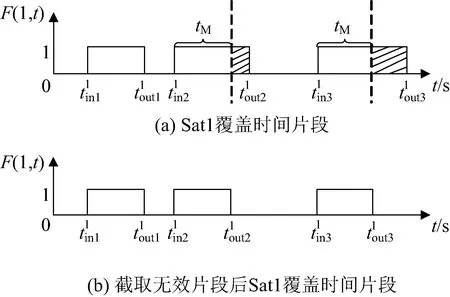
图3 Sat1覆盖时间片段截取Fig.3 Selecting time fragments for Sat1

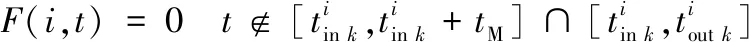
(5)

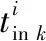
经过处理后得到了卫星对目标区域的覆盖情况，由于去除的时间片段可能包含卫星对某个网格点的覆盖时间片段，故需将处理后的时间片段与步骤二中得到的卫星对网格点的覆盖片段相比较，确定卫星对目标区域内所有网格点的覆盖情况。如图4所示，图4(a)为处理后的卫星对目标区域的覆盖情况，图4(b)为卫星对网格点的覆盖情况。当卫星对目标区域的覆盖时间片段与卫星对网格点的覆盖时间片段存在重复时间片段时，则该网格点能被卫星覆盖，当不存在重复时间片段时，则该网格点无法被覆盖，例如图4(b)中网格点4就无法被卫星Sat1覆盖。卫星i对网格点j的覆盖状态函数可用R(i,j)表示，当网格点j能被卫星i覆盖时取1，否则取0，如式(6)和式(7)所示。

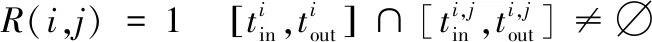
(6)

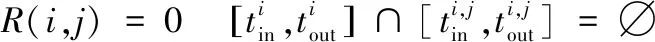
(7)

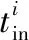
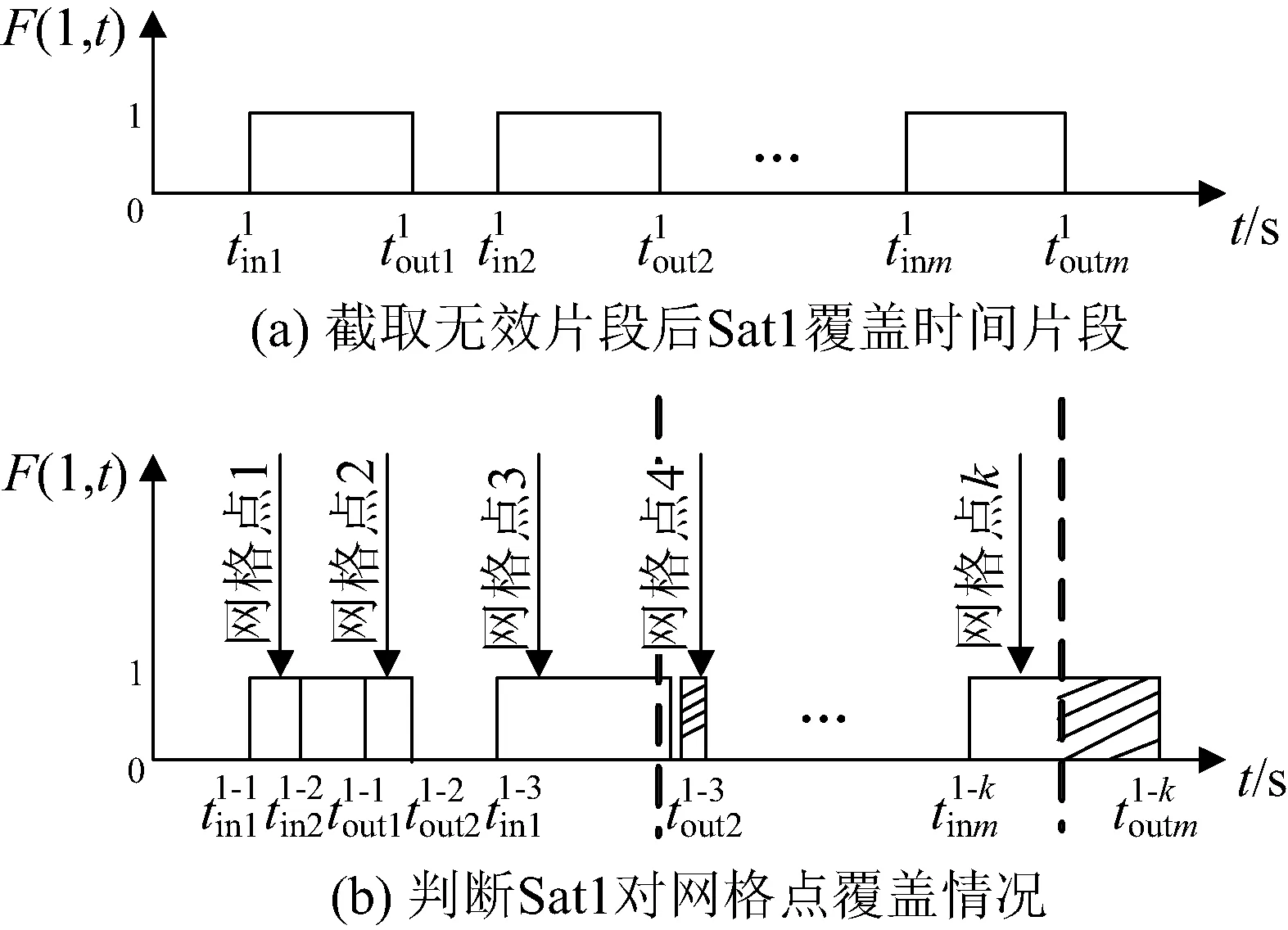
图4 Sat1对网格点覆盖Fig.4 Coverage of grid points by Sat1

通过计算可得到星座中所有卫星对目标区域内网格点的覆盖情况，当星座中存在一颗卫星对网格点j覆盖，即表示网格点j能被星座覆盖。统计星座对网格点的覆盖情况，计算覆盖百分比Pcov，如式(8)所示。统计星座中每颗卫星对区域的覆盖时段，合并重复时间段，得到星座对目标区域的覆盖时段。星座第k次覆盖目标的结束时刻为tout k，星座第k+1次覆盖目标的开始时刻为tin k+1，计算最大重访时间Trevisit，如式(9)所示。

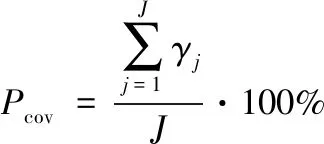
(8)

Trevisit=max(tin k+1-tout k)(k=1,2,3，…，B-1)

(9)

式中：J为网格点数量；γj为星座对网格点j的覆盖情况，当能够被星座覆盖时取1，否则取0；B为区域目标被星座覆盖总次数。

对于成像卫星而言，空间分辨率和瞬时覆盖面积是表征覆盖质量高低的关键指标。瞬时覆盖面积由卫星的轨道高度和载荷的视场角决定。空间分辨率指图像上能够详细区分最小单元的地面尺寸[17]，当载荷工作方式为被动成像时，如CCD相机、红外热成像仪，空间分辨率可通过式(10)计算；当载荷工作方式为主动成像时，如微波辐射仪，空间分辨率可通过式(11)计算。

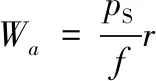
(10)

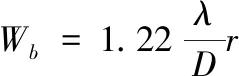
(11)

式中:Wa为被动成像载荷空间分辨率；Wb为主动成像载荷空间分辨率；pS为像元大小；f为相机焦距；r为载荷到目标的距离；λ为载荷工作波长；D为镜头直径。

对星座覆盖能力综合评估时，可通过覆盖能力指数度量星座覆盖能力的强弱。由于不同性能指标的单位不同，数值差异较大，需对各指标值进行标准化后，结合各指标在任务中的重要程度，计算可得星座覆盖能力指数，如下式所示，覆盖能力指数越大，星座覆盖能力越强。

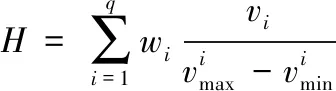
(12)

2 星座成本及度量方法

星座任务的成本往往与性能和可靠性有关，三者呈相互制约关系[18]。随着星座任务成本的增大，星座的性能、可靠性其中之一或两者都会提升。星座设计的准则为在有限的星座成本和可接受的可靠性范围内最大化的提升星座性能。目前星座成本估计方法可分为参数法、类比法和工程法。参数法依赖于原始数据集，通过对数据进行回归分析，创建成本估算关系。相比于其他方法，它体现了统计的客观性和一致性，是一种较为普遍的成本估算方法。通过参数法建立的星座成本估计模型有：Unmanned Space Vehicle Cost Model(USCM)、SSCM、NASA Instrument Cost Model(NICM)等[19]。

整个星座的成本估计需要考虑卫星本体研发制造、测试、地面系统、发射系统以及星座持续运营等过程。对星座成本进行估计首先需对单个卫星成本进行估计，卫星总成本可用式(13)表示。如图5所示，单个卫星成本由载荷、集成&装备&测试、卫星平台、运行控制、地面支持设备和发射子系统成本共同组成。本文选用SSCM模型对卫星系统成本进行估计[20]，通过卫星的质量可以直接获得卫星的平台成本，如式(14)所示。卫星载荷、集成&装备&测试、运行控制、地面支持设备和发射成本计算可通过平台成本和相对于平台成本的比例系数进行计算，相对系数见表1[20]。

Ctotal=Cpayload+CIA&T+Cspacecraft+Cprogram+

Cground+Claunch

(13)

Cspacecraft=781+26.1m1.261

(14)

式中:Ctotal为单个卫星总成本，成本单位均为K$，以2000年财政收入为基准；Cpayload为载荷系统成本；CIA&T为集成、装备和测试成本；Cspacecraft为卫星平台成本；Cprogram为运行控制成本；Cground为地面支持设备成本；Claunch为发射成本；m为卫星干重。

考虑到多批相同卫星制造时存在并行化加工和批量测试的情况，成批量生产中单个卫星所需的成本会远小于只生产单颗卫星时所需要的成本，可对整个星座所需的成本分为循环成本和非循环成本,如式(15)所示。循环成本表示在制造过程重复加工所需的成本，非循环成本表示星座中只需进行一次生产过程所需要的成本。表1列出了载荷、集成&装备&测试、卫星平台、运行控制、地面支持设备和发射6个子系统中循环成本和非循环成本所占对应子系统的成本比例[20]。星座的循环成本可通过式(16)表示。

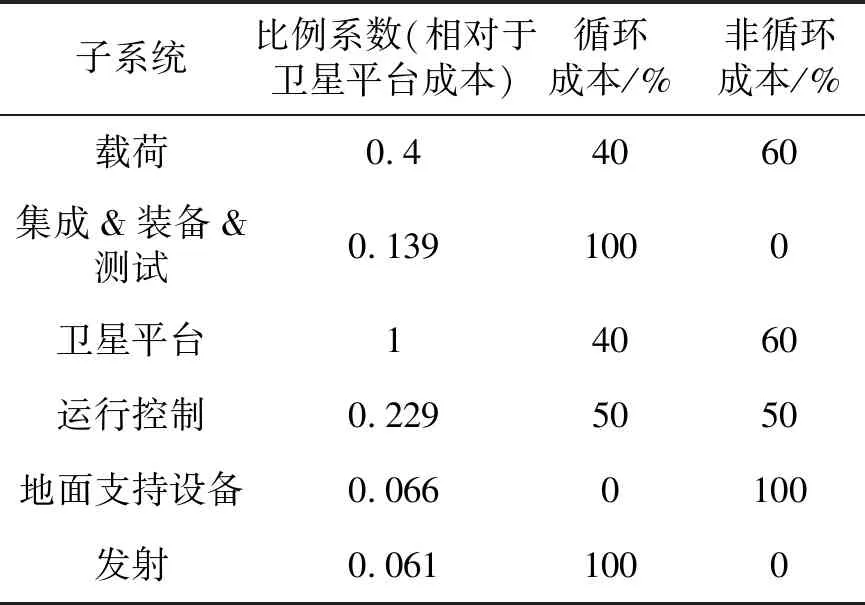
表1 卫星分系统成本比例

Cconstellation=Cnonrec+Crec

(15)

Crec=Crec_satn1-log 2(1/b)

(16)

式中：Cnonrec为星座非循环成本；Cconstellation为星座总成本；Crec为星座循环成本；Crec_sat为单个卫星循环成本；n为星座中的卫星数量；b为学习因子，一般取0.67。

3 星座弹性及度量方法

随着空间碎片质量和数量的增加，航天器在太空面临的威胁越来越大。对于小卫星而言，卫星本体中未装载多余备份系统，注定其一旦遭遇碎片撞击就会面临失效的风险。当小卫星侦察星座遭遇卫星故障，碎片碰撞等不利影响时将导致性能下降，故星座能否在性能下降后依然具有完成基本任务的能力是衡量星座弹性的标准。对星座失效状态进行分析，单颗卫星状态可分为正常和失效状态，卫星失效状态的概率为τ，则正常状态的概率为1-τ，卫星状态相互独立，卫星失效概率满足伯努利分布，则k颗卫星失效概率为ρk:

ρk=τk(1-τ)n-k

(17)

式中：n为卫星数量；τ为卫星失效概率，一般取0.05～0.1。

本文提出星座性能损失率指标可有效表征星座弹性能力的强弱。星座性能损失率定义为星座中一定量卫星失效，性能指标下降幅度最大值相对于星座满站位状态下性能指标值的百分比，可用星座满站位性能指标值和失效状态下的性能指标值表示，失效状态下的性能指标值指卫星失效导致性能指标下降幅度最大的性能指标值。例如星座中存在1颗卫星失效，卫星3失效后导致对目标的覆盖百分比下降幅度最大，则星座在单颗卫星失效状态下的覆盖百分比即为卫星3失效后星座对目标的覆盖百分比。当星座中存在k颗卫星失效时，星座性能损失率Qk，如式(18)所示。对于无法确定星座中卫星失效数量的情况下，星座性能损失率取决于星座k颗卫星失效的概率和k颗卫星失效状态下的星座性能损失率Qk为：

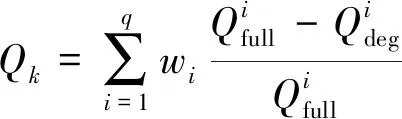
(18)

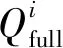
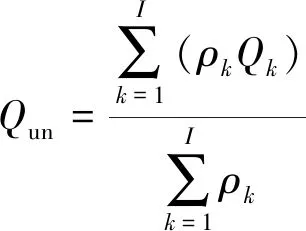
(19)

式中：Qun为星座失效卫星数量未知情况下的星座性能损失率；I为星座最多失效卫星数目。

4 仿真评估

为了验证指标选取及度量方法的有效性，现对SkySat和吉林一号星座的覆盖、成本和弹性进行评估。SkySat是美国商业遥感公司Skybox于2013年提出的小卫星星座，所有卫星质量不超过110 kg，至2018年底已发射15颗卫星，致力于全球高分辨率遥感全色多光谱图像和视频录像信息获取，视频录像分辨率高达1.1 m，最大录像时长90 s[21]。吉林一号是中国长光卫星技术有限公司研制的小卫星星座，所有卫星质量不超过500 kg，至2018年底已发射10颗卫星，星上载荷具备高光谱图像和动态视频拍摄能力[22]。

仿真时间：2020-02-13 00:00:00～2020-02-14 00:00:00，时间步长60 s。假定SkySat和吉林一号均具有随时进行中继数据的传输能力，星座中卫星参数均相同，部分参数见表2[21-22]，目标区域在星地下传链路区域内的比例为0.5，对SkySat和吉林一号星座的覆盖能力进行分析。以6°的纬度间隔将目标区域等面积划分为25个网格，选取覆盖百分比、最大重访时间、平均响应时间和覆盖总时间4个覆盖特性指标进行分析，仿真结果如表3所示。

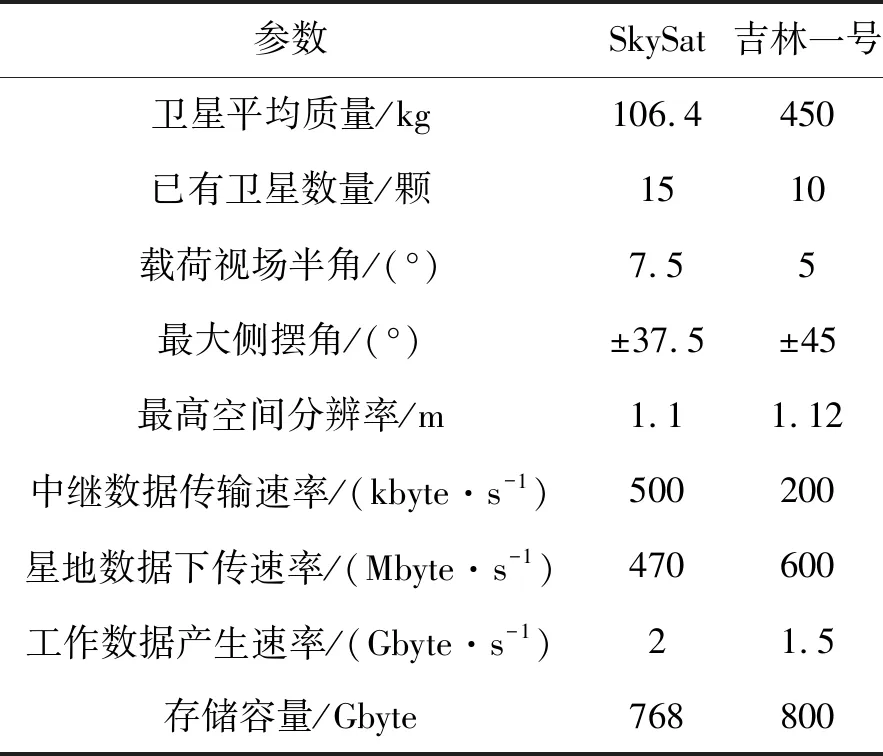
表2 SkySat和吉林一号星座主要参数

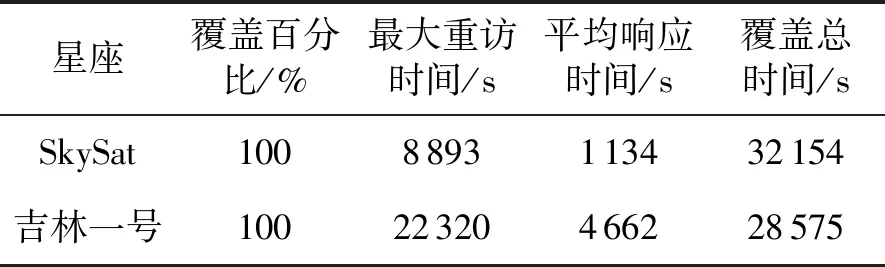
表3 SkySat和吉林一号星座覆盖性能指标

通过层次分析法可以得到覆盖百分比、最大重访时间、平均响应时间和覆盖总时间在覆盖能力中的权重依次为0.5、0.316 7、0.130 3、0.053 1。根据表3和式(12)可计算出SkySat和吉林一号的覆盖能力指数分别为0.485、0.429。

利用前面提到的星座成本估计模型，对SkySat和吉林一号的成本进行分析。由表2可知，SkySat星座中卫星平均质量为106.4 kg，通过式(14)可计算出单颗卫星平台成本为10 170千美元，根据表1中其他子系统相对于平台成本的比例系数可得出载荷、集成&装备&测试、程序控制、地面支持设备和发射&轨道保持5个子系统的成本分别为4 068，1 414，2 329，671，620 千美元。由表1中循环成本在子系统成本中所占的比例可以计算出单颗卫星中每个子系统的循环成本和非循环成本，如表4所示。

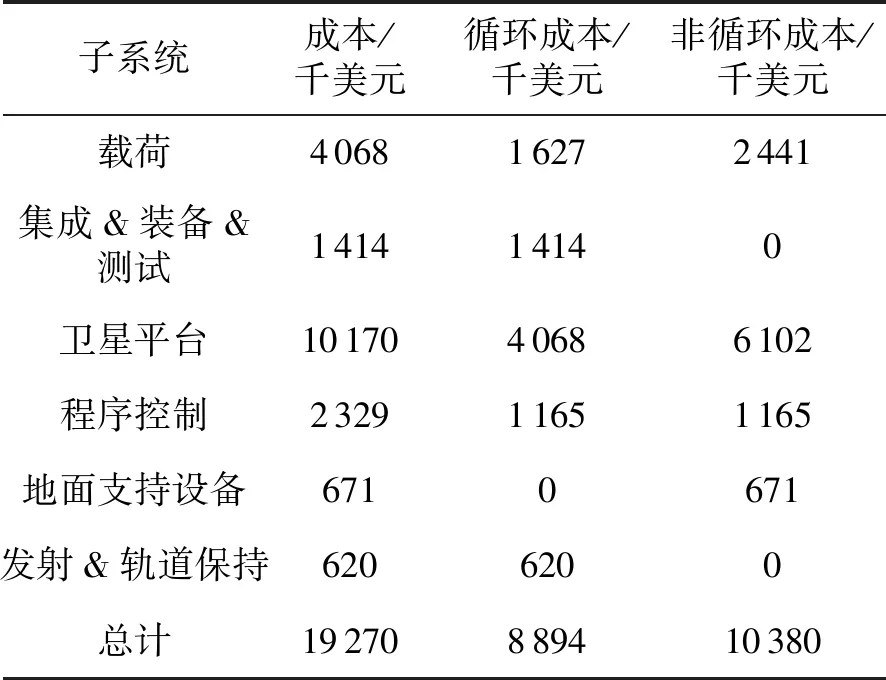
表4 SkySat单颗卫星子系统成本

由表4可知单颗卫星的循环成本为8 894千美元，根据式(15)可得SkySat星座的循环成本为27 910千美元，单颗卫星的非循环成本即为星座的非循环成本，将星座循环成本和非循环成本带入式(16)可得SkySat星座成本为38.29百万美元。同样，计算可得吉林一号星座的成本为195.41百万美元。

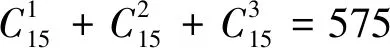
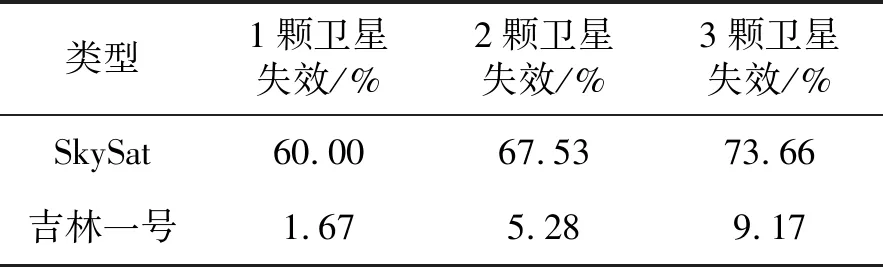
表5 SkySat星座性能损失率指标

根据星座失效概率函数可知星座失效1、2、3颗的概率分别为0.038 7、0.002 5、0.000 3。结合表5和式(19)分别计算出SkySat和吉林一号的星座性能损失率为0.605、0.021。

分别比较SkySat和吉林一号星座的覆盖能力指数、成本和星座性能损失率，结果表明SkySat的覆盖能力和成本均优于吉林一号，而吉林一号的弹性能力优于SkySat。

5 结束语

本文针对小卫星侦察星座的性能评估问题，提出了覆盖、成本以及弹性三类指标，分别建立了各类指标的计算模型。相比于传统覆盖计算方法，本文考虑到卫星存储容量对星座覆盖性能的影响，将存储容量作为约束，结合卫星对地覆盖模型分析了小卫星对地覆盖的条件，提出了考虑存储容量的网格点法对小卫星星座的覆盖性能指标进行计算；采用SSCM模型对小卫星星座成本进行计算；对小卫星侦察星座状态的失效概率进行了分析，并提出了星座性能损失率指标，用于小卫星星座的弹性能力评估。对SkySat和吉林一号进行性能评估，试验结果表明，本文提出的三个模型均可用于评估星座覆盖、成本和弹性能力的优劣，能够为小卫星侦察星座建设和性能评估提供参考，下一步可在三类指标之间权衡考虑，对区域侦察弹性星座进行设计。