基于动态故障树的卫星可靠性分析
2020-11-26王许煜胡敏张学阳赵玉龙李玖阳
王许煜,胡敏,张学阳,赵玉龙,李玖阳
航天工程大学,北京 101400
随着国内外航天技术的快速发展,卫星已经被广泛应用于通信遥感、导航定位和军事侦察等领域。然而作为一类特殊产品,卫星具有其他产品不具备的特点[1-2]:一是卫星设计和制造周期长,成本高且生产数量少;二是卫星需要苛刻的发射条件,且会长期受到复杂恶劣的太空环境的影响;三是若卫星在轨运行期间发生故障,无法对其进行有效的人为维修。因此,通常把卫星称为四高产品,即高技术、高投入、高效益和高风险产品[3]。对于卫星星座而言,卫星可靠性关系到星座可用性和备份策略的选取[4],所以为了能够连续稳定地完成特定任务,需要对卫星可靠性进行分析,以确保卫星的高可靠性。
目前传统的卫星可靠性模型通常采用指数模型,然而该简化模型虽然有利于分析问题,但不能准确地描述卫星早期故障和损耗累积的过程。文献[5-6]利用多个概率分布的组合来表示卫星各个寿命阶段进行可靠性建模。文献[7]借鉴GPS卫星的经验,分别采用Weibull分布模型和正态分布模型模拟卫星随机故障和损耗故障,进而建立卫星可靠性模型。利用分布模型建模虽然能反映卫星的实际情况,但由于卫星系统可靠性高,失效样本十分有限,导致模型参数难以确定,不利于可靠性模型的准确建立。文献[8]提出基于序贯优化和可靠性分析的交叉熵优化方法,对卫星可靠性设计进行优化分析。文献[9]利用贝叶斯网络模型提出一种基于不确定隶属度函数和区间特征量的复杂不确定系统可靠性分析方法。这些方法虽然能有效分析卫星可靠性,但都无法准确描述卫星系统内部各组件之间复杂的动态逻辑关系。本文利用动态故障树方法对卫星系统进行分析,为其可靠性设计分析提供了一个新的思路。
传统的故障树分析法(fault tree analysis,FTA)是一种分析系统可靠性的有效方法[10],但其不适用于具有动态失效行为的复杂系统。马尔可夫模型虽然可以表达系统的动态特性,但是由于模型的状态空间数量会随系统规模的增长呈指数增长,而导致模型的建立和求解十分复杂[3]。动态故障树(dynamic fault tree,DFT)分析方法结合了传统FTA分析方法和Markov模型两者的优点,它通过引入描述系统动态特征的逻辑门建立相应的动态故障树,并将其转化为马尔可夫模型,从而能够对动态系统进行可靠性和安全性分析,被广泛应用于动态系统的可靠性建模[11]。
本文首先采用马尔可夫链和二元决策图相结合的分析方法,建立卫星的电源、姿轨控和推进3个分系统的动态故障树模型,在此基础上得到卫星的随机故障模型,并综合考虑损耗故障建立卫星可靠性模型。接着利用蒙特卡洛仿真对随机故障模型进行评估分析,最后将其与Weibull分布模型进行性能比较。
1 动态故障树理论
1.1 动态故障树
故障树是一种特殊的树状逻辑因果关系图,它用规定的事件、逻辑门和其他符号描述系统中各事件之间的因果关系[12]。动态故障树是指包含一个或多个动态逻辑门的故障树,与传统的故障树相比,由于其引入了能够表征系统动态时序特性的元素,可以用于复杂冗余系统的分析求解。
动态故障树中的动态逻辑门是描述事件之间因果关系的逻辑符号,其能够用来表征与事件发生顺序相关的动态特性,这些特性必须考虑不同底事件的发生顺序以及各组件之间的依赖关系[12]。动态逻辑门主要有:优先与门、顺序相关门、功能相关门、冷备件门、温备件门和热备件门等[13]。
(1)优先与门
优先与门(priority-AND gate, PAND)具有两个底事件A和B,只有这两个底事件按照从左到右的顺序依次发生时才会导致顶事件的发生,图1表示优先与门转化为马尔可夫链的过程。其中,状态的第一个数字表示底事件A的状态,第二个数字表示底事件B的状态,数字1和0分别表示底事件故障和正常的两种状态。Fa和Op分别表示顶事件T发生和不发生。转移路径上的符号表示相应事件发生故障,其转移率为该事件的失效率。
(2)顺序相关门
顺序相关门(sequence enforcing gate, SEQ)具有多个底事件,当底事件按照从左到右的顺序依次发生时顶事件T才发生。以3个底事件为例说明顺序相关门转化为马尔可夫链的过程,如图2所示。

图2 顺序相关门转化为马尔可夫链的过程Fig.2 The process of transforming sequence enforcing gate into Markov chain
(3)功能相关门
功能触发门(functional dependency gate, FDEP)表示系统中各个事件之间的关系,并没有实际的输出,若系统中的触发事件T发生,则与其相关的所有基本事件A和B都发生,而基本事件的发生对触发事件的发生则没有任何影响。图3为功能相关门转化为马尔可夫链的过程。
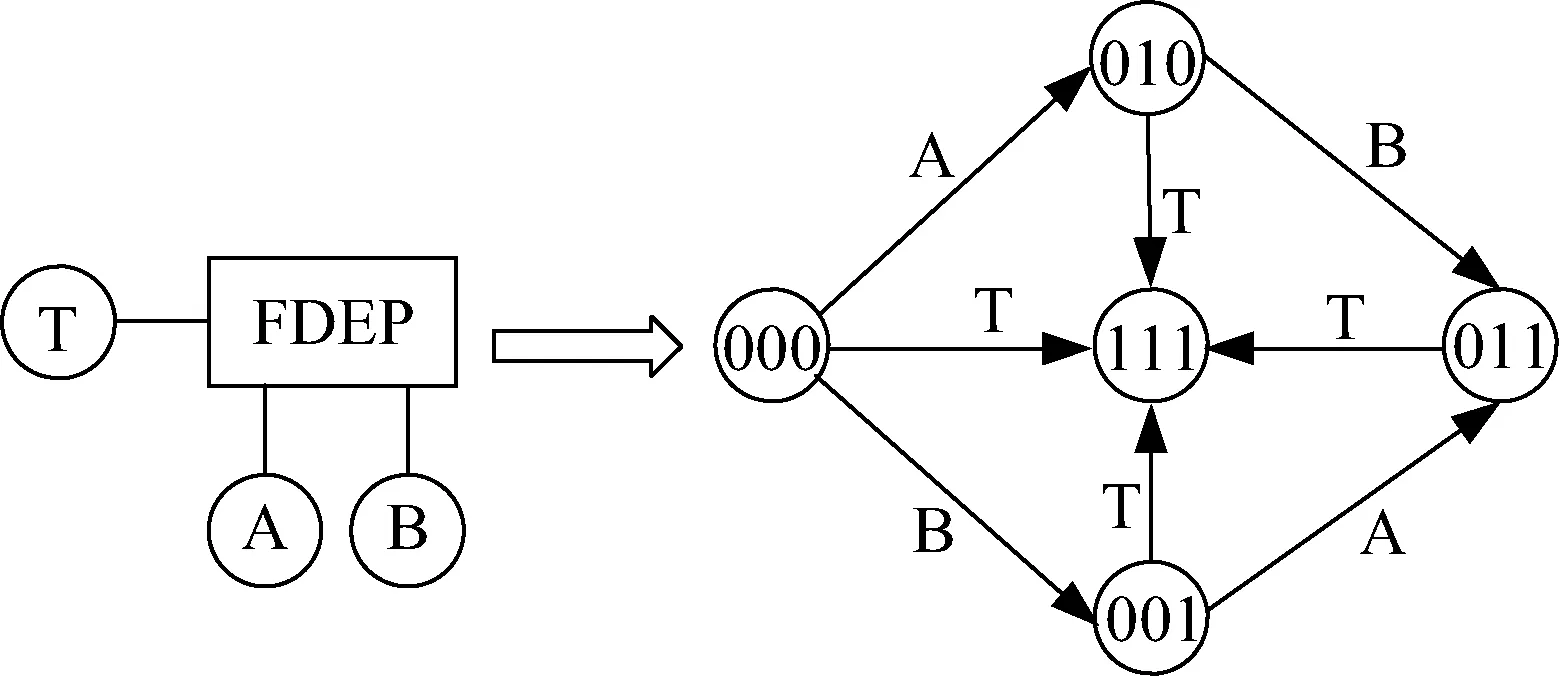
图3 功能相关门转化为马尔可夫链的过程Fig.3 The process of transforming functional dependency gate into Markov chain
(4)冷备份门
冷备件门(cold spare gate, CSP)包括一个主件和至少一个冷备件。系统运行时主件处于正常工作状态,其余的冷备件处于不工作状态,且失效率为零。当主件A发生故障时,冷备件开始工作,直至所有冷备件失效,顶事件T才会发生。图4冷备份门转化为马尔可夫链的过程。

图4 冷备件门转化为马尔可夫链的过程Fig.4 The process of transforming cold spare gate into Markov chain
(5)温备份门
温备件门(warm spare gate, WSP)的逻辑关系与冷备件门基本相同,不同的是当系统主件工作时,温备件处于预工作状态具有一定的失效率,但小于正常工作状态下的失效率, 只有主件与温备件都发生故障时顶事件T才会发生。图5是温备件门转化为马尔可夫链的过程。
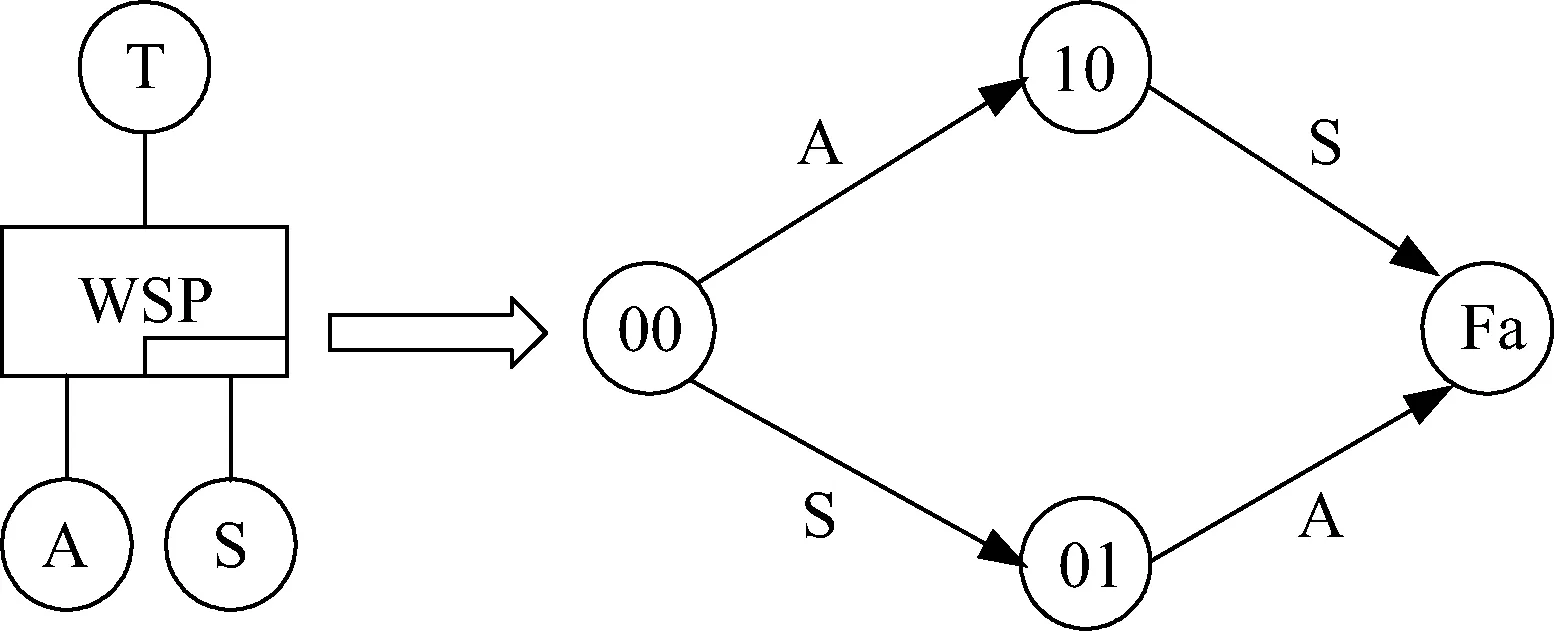
图5 温备件门转化为马尔可夫链的过程Fig.5 The process of transforming warm spare gate into Markov chain
(6)热备份门
热备件门(hot spare gate, HSP)中的主件A和热备件都处于正常工作状态,热备件具有正常工作状态下的失效率。当主件与热备件都发生故障时顶事件T才会发生。图6是热备件门转化为马尔可夫链的过程。
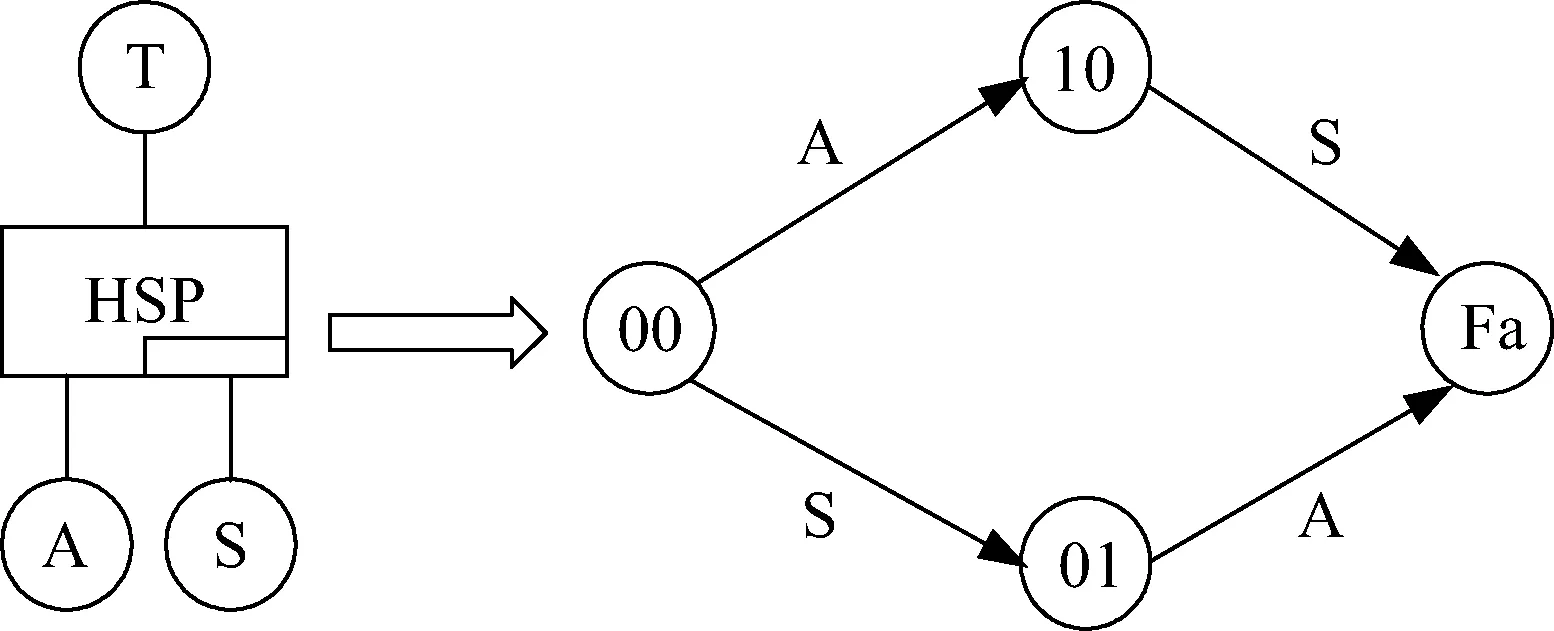
图6 热备件门转化为马尔可夫链的过程Fig.6 The process of transforming hot spare gate into Markov chain
1.2 动态故障树的分析方法
在动态故障树模型中通常只有很少的逻辑门具有动态特性。所以在动态故障树分析中,首先利用线性搜索算法对DFT进行模块化分解,该算法通过对DFT进行两次深度优先最左搜索(DFLM)[12],得到相互独立的动态子树和静态子树,其中包含动态逻辑门的子树为动态子树,只有静态逻辑门的子树则为静态子树。通过模块化处理后,复杂系统的DFT被分解成多个子模型,极大简化了模型的求解过程[14]。然后对不同类型的子树单独求解,利用二元决策图(binary decision diagram,BDD) 对静态子树进行求解, 而动态子树则转化成相应的Markov 链进行求解。最后结合各独立子树分析求得的故障概率进行综合分析,通过逻辑关系自下而上分步求解直至获得动态故障树的顶事件发生概率。动态故障树的整个分析过程如图7所示。
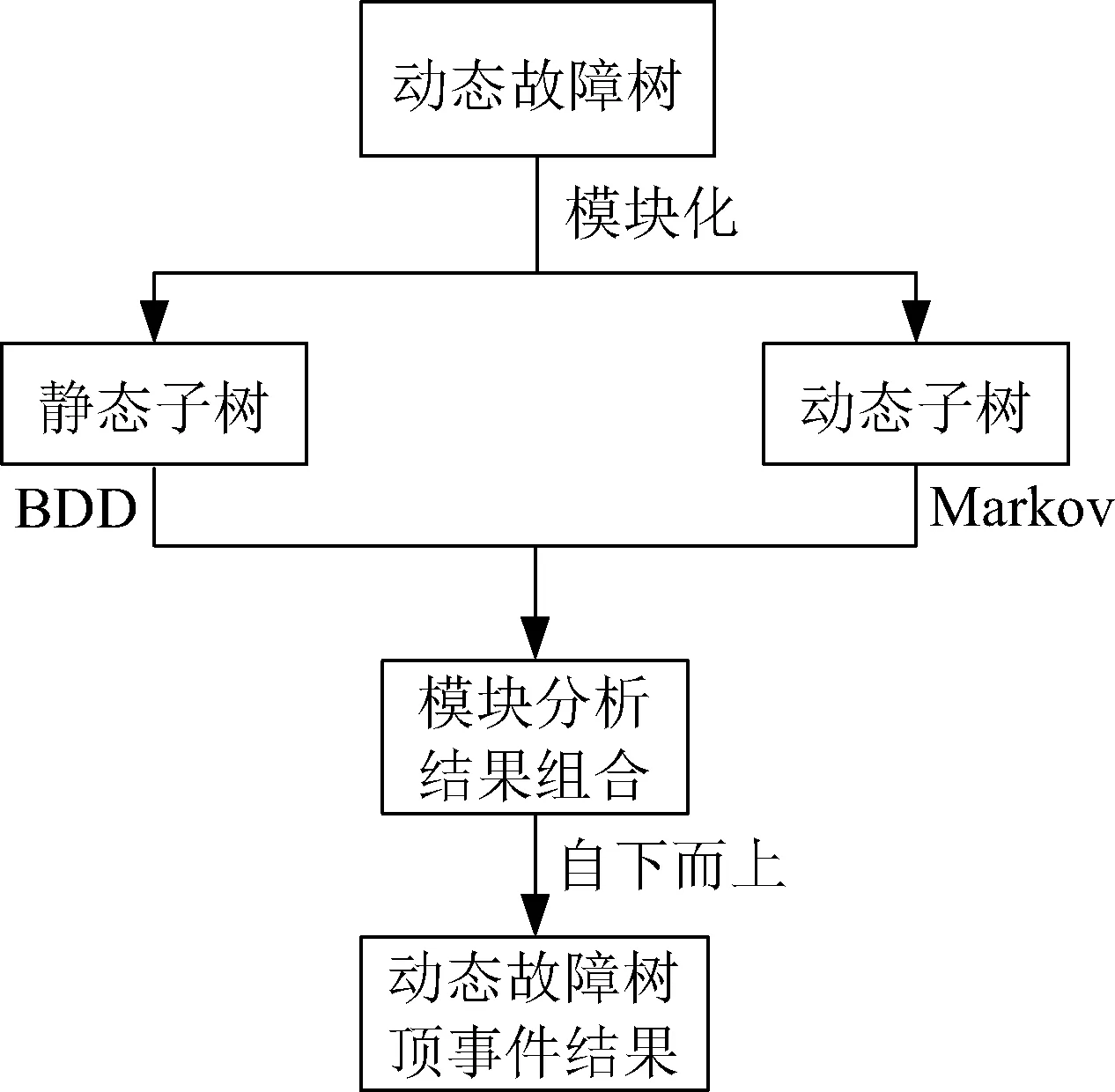
图7 动态故障树模型分析过程Fig.7 Dynamic fault tree model analysis process
2 卫星可靠性模型分析
卫星主要由航天器平台和有效载荷两大部分组成,其中航天器平台包括结构分系统、电源分系统、数管分系统、测控分系统、姿轨控分系统、推进分系统以及热控分系统。图8为卫星的简要故障树。根据卫星在轨故障的统计结果显示[15-16],对于卫星而言,电源、姿轨控和推进3个分系统在轨故障所占比例最高,而且一旦该系统发生故障将直接影响航天器的正常运行。本文重点针对这3个分系统展开分析。

图8 卫星简要故障树Fig.8 Satellite fault tree
2.1 动态故障树建模
(1)电源分系统
目前,卫星上大多采用太阳电池翼-蓄电池组的电源系统,由两条相同的供电母线并联组成,以提高系统的可靠性,每条母线包括蓄电池组、太阳电池阵以及电源控制器。其中,蓄电池组采用锂离子蓄电池组,该蓄电池组由4组蓄电池并联组成,每组蓄电池由9个单体串联而成,并假设每个单体都一样。电源系统的动态故障树模型如图9所示。
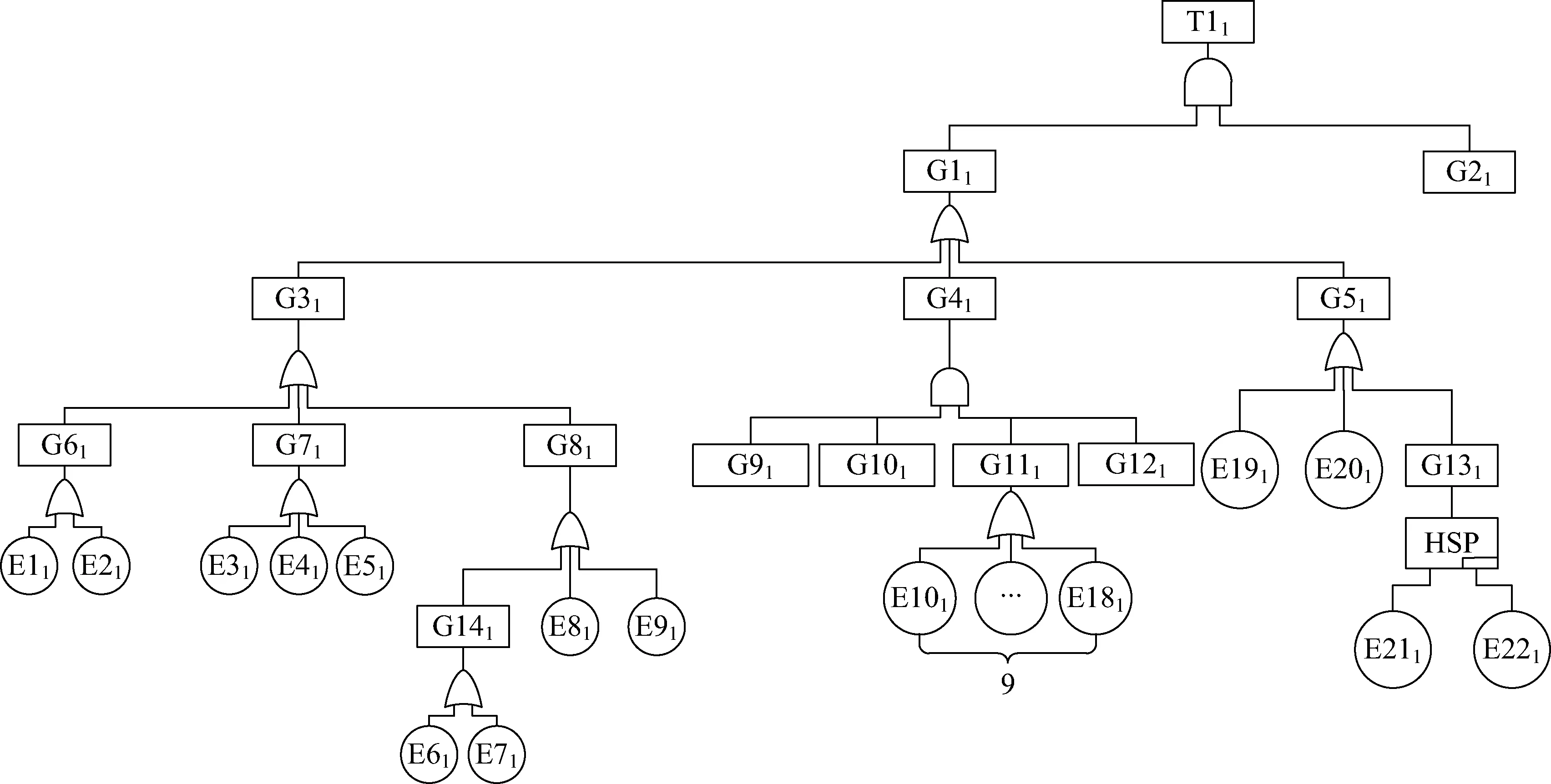
图9 电源系统的动态故障树模型Fig.9 Dynamic fault tree model of power system
模型中各事件说明如表1所示。

表1 电源系统动态故障树模型事件说明
(2)姿轨控分系统
卫星姿轨控分系统多数采用精度高、稳定性好的三轴姿态稳定控制方式,主要由控制器子系统、执行机构子系统和姿态确定子系统组成,它们之间通过相互作用实现卫星姿态的闭环控制。其中,执行机构采用三正一斜装的反作用轮,并利用磁力矩器和推力器对其进行卸载。姿态确定系统则采用陀螺和星敏感器的组合,同时将太阳敏感器和两个红外地平仪作为星敏感器的备份。姿轨控系统的动态故障树模型如所图10所示。
模型中各事件说明如表2所示。
(3)推进分系统
卫星采用双组元统一推进系统,其技术成熟,被广泛应用于长寿命航天器上。该系统利用气瓶将燃烧剂(MMH)和氧化剂(MON-1)以雾化的形式推出,并通过气管和各类阀门进入燃烧室,在按一定的比例燃烧后产生推力。推进分系统的故障树模型如图11所示。
模型中各事件说明如表3所示。

图10 姿轨控分系统的动态故障树模型Fig.10 Dynamic fault tree model of attitude and orbit control system
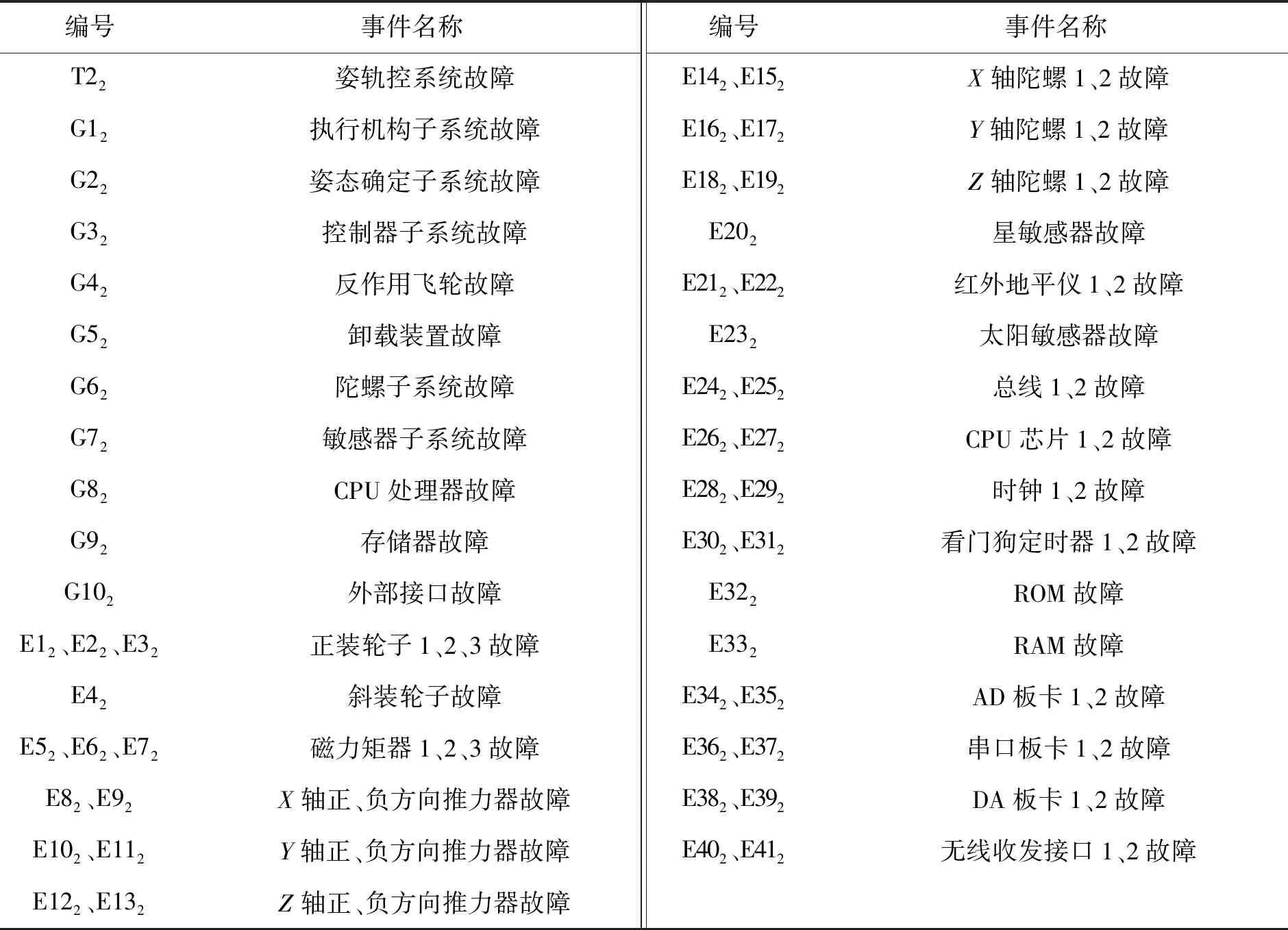
表2 推进分系统动态故障树模型事件说明
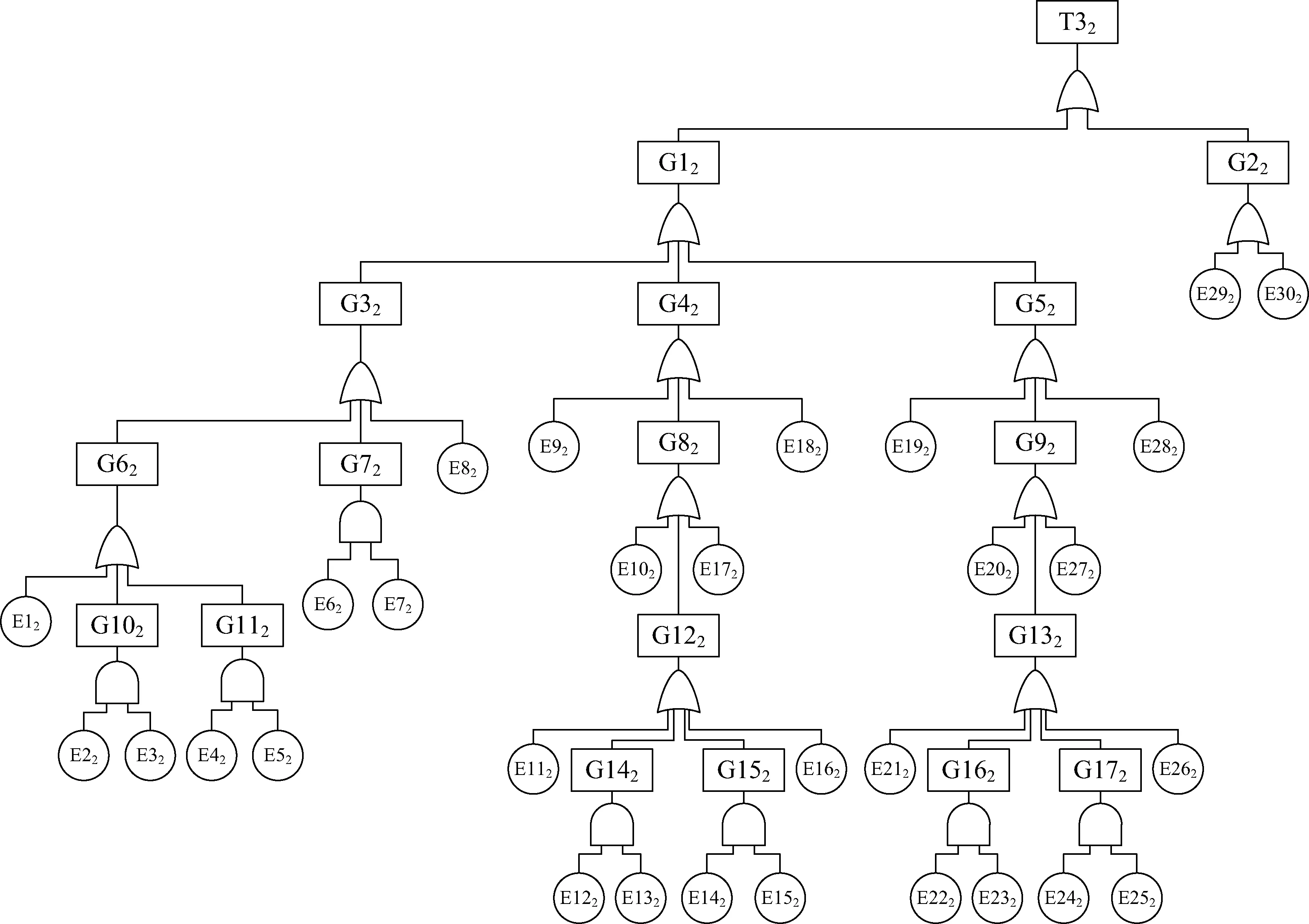
图11 推进分系统的故障树模型Fig.11 Fault tree model of propulsion system

表3 推进分系统故障树模型事件说明
2.2 基于BDD的静态子树分析
卫星系统动态故障树模型规模较大,本文将以电源系统为例详细分析动态故障树模型的求解过程,其余两个系统将以同样的方法进行分析。由于两条供电母线相互独立且组成相同,所以可对供电母线1进行单独分析,将动态故障树进行模块化分解,得到相应的静态子树和动态子树,其中静态子树包括G31、G41和G51,动态子树包括G131。
对于静态子树,采用BDD进行求解。BDD 是一个有向无环图[17],由根节点、叶节点和中间节点组成。每条BDD路径从根节点开始,经过中间节点时进行布尔函数的计算,并有两条分支,分别代表事件失效和正常两种状态,最终到达叶节点。叶节点有两种类型,其中“1”表示系统故障,“0”表示系统正常。
(1)G31静态子树
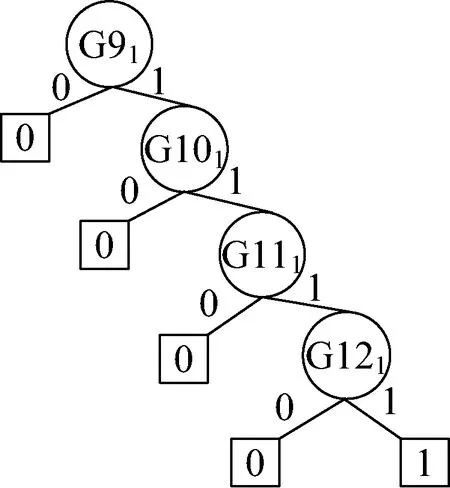
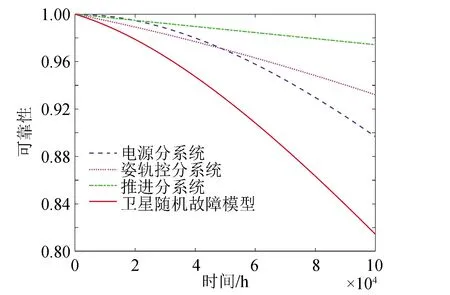
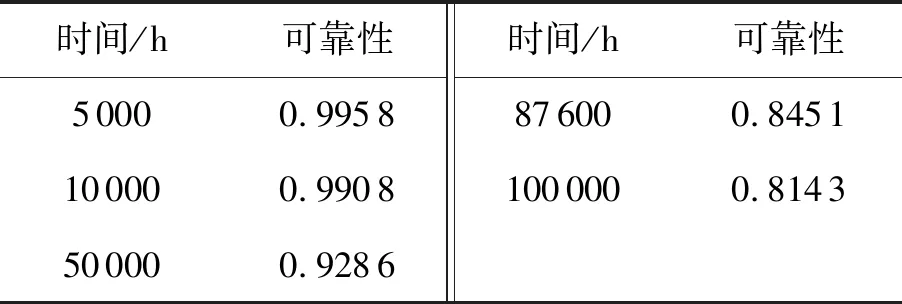
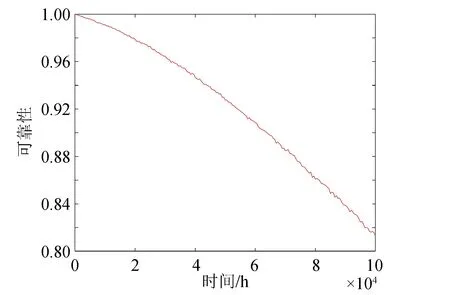
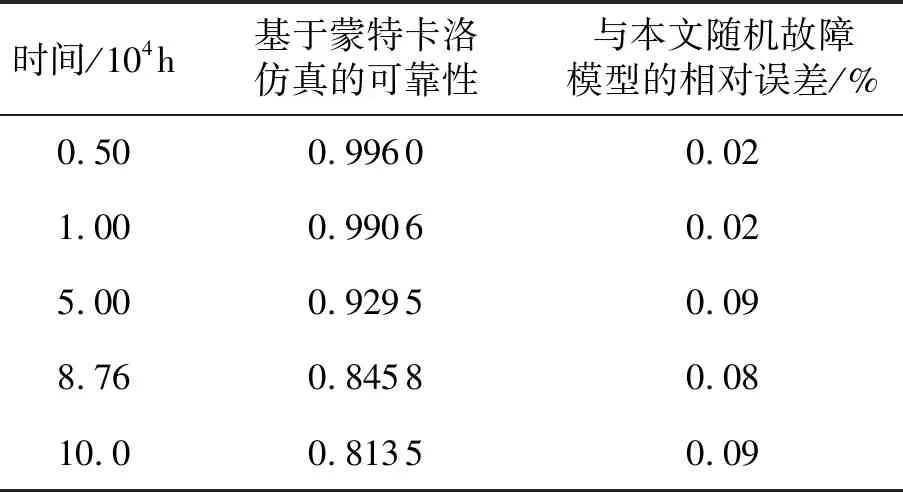
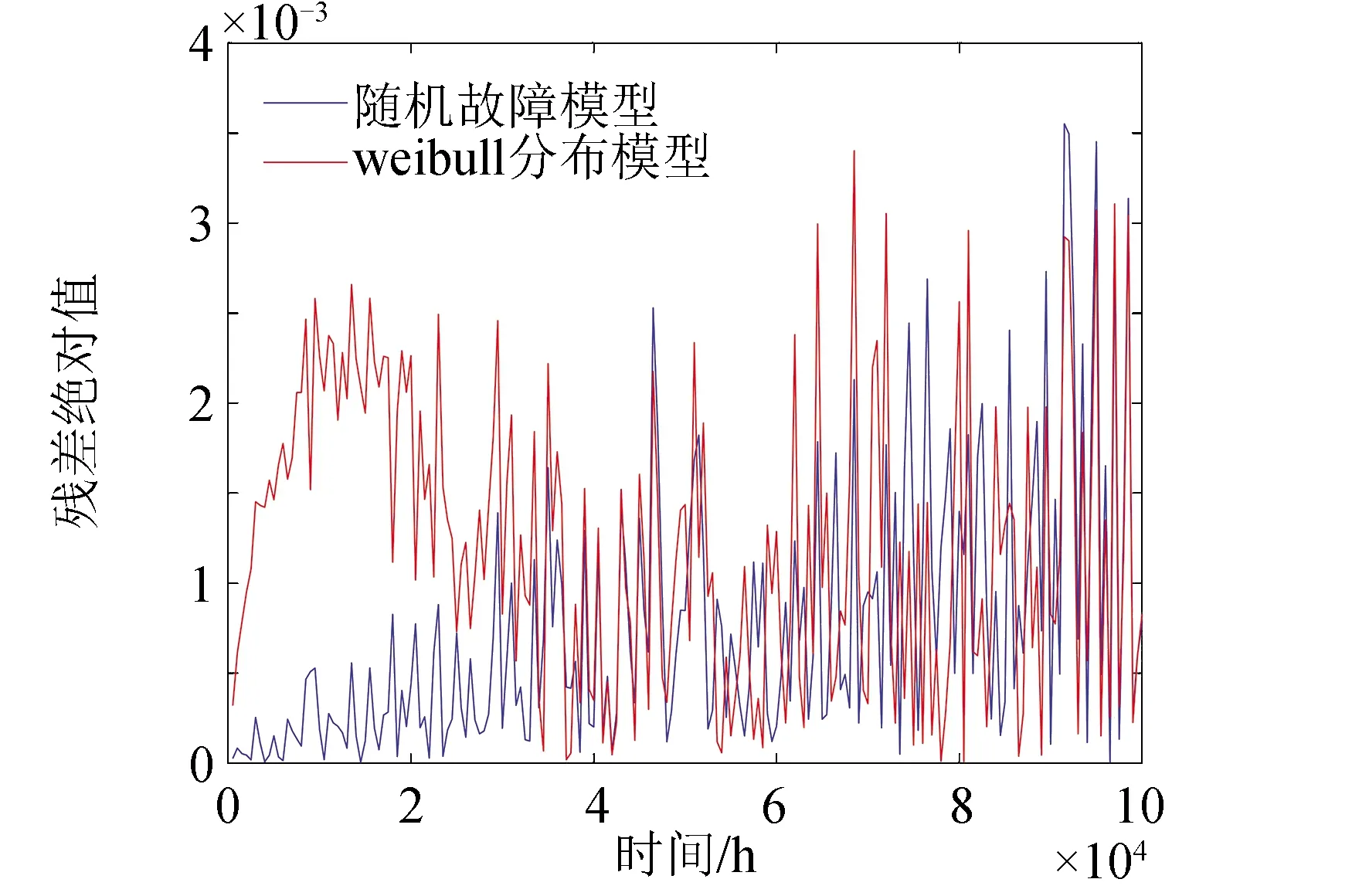
将G31静态子树进行BDD分解首先要确定底事件的最优指标顺序,为便于计算,假设指标顺序为:E11 根据BDD可以得G31事件发生的概率为: P(G31)=P(E11∪E21∪E31∪E41∪E51∪ E61∪E71∪E81∪E91)=1- (1) 图12 G31静态子树的BDDFig.12 BDD for G31 static subtree (2)G41静态子树 由于G41静态子树由4个相同的中间事件并联所得,所以为了简化分析,先对其中一个中间事件G111进行单独分析,然后再结合其余事件进行综合分析。G111由9个底事件串联所得,所以可以根据其组成结构得到G111发生的故障概率为: P(G111)=1-[1-P(E101)]9 (2) 然后将G91、G101、G111、G121当作G41的底事件进行分析,假设底事件指标顺序为:G91 图13 G41静态子树的BDDFig.13 BDD for G41 static subtree 根据BDD可以得G41事件发生的概率为: P(G41)=P(G91G101G111G121) (3) (3)G51静态子树 对于G51静态子树,由于热备份件门的存在,首先要将动态子树G131作为其输入底事件,假设底事件指标顺序为:E191 根据BDD可以得G51事件发生的概率为: P(G51)=P(E191∪E201∪G131)= (4) 最终,结合各模块事件的发生概率,可以得到供电母线1的故障概率,并进一步得到电源系统T11的故障概率。 P(T11)=P(G11G21)=P(G11)P(G21)= (5) 根据动态故障树模块化分析可得,电源动态故障树中只有G131为动态子树,对于动态子树,将采用Markov链进行求解。Markov链是用来表示系统各状态之间转换的一种方法,由于系统下一时刻的状态只与当前时刻的状态有关,而与之前任何时刻无关,所以具有“无记忆性”。在Markov 链中圆圈代表系统当前时刻的状态, 有向线段表示状态的转移方向,而上面的权值则表示状态的转移概率。 求解马尔可夫链的方法有很多,文献[18]提出将系统的Markov状态转移图分解成多条状态转移链,并推导出不同链长的转移链的概率计算公式,进而求得动态子树的发生概率。链长为n的状态转移链Tn的概率计算公式: (6) 式中:λi-1,i>0,为状态i-1到状态i的转移率;λi-1,Op≥0,为状态i-1到状态Op的转移率。 由图6可得热备件门具有两条链长为2的状态转移链,根据式(6)计算各链的概率,然后将其相加,就可得到动态子树G131的发生概率,最后将所得概率代入(4)中进而得到电源系统的故障概率。 假设电源系统各部件的寿命均服从指数分布,且各底事件的失效率如表4所示。设卫星在轨工作时间为105h,寿命末期为8.76×104h。 表4 电源分系统各底事件失效率 将相关数据代入模型,得到卫星电源分系统的可靠性随时间变化曲线,如图15所示。 图15 电源分系统的可靠性随时间变化曲线Fig.15 Reliability curve of power system with time 利用动态故障树方法分别对姿轨控分系统和推进分系统进行分析,并最终得到卫星随机故障模型的可靠性随时间变化曲线,如图 16所示。由图 16可知,随着卫星工作时间的增长,卫星及3个分系统的可靠性都在逐渐下降,同时电源分系统对卫星可靠性的影响在逐渐增大,到卫星寿命末期时,成为3个分系统中最为薄弱的环节。 图16 卫星随机故障模型的可靠性随时间变化曲线Fig.16 Reliability curve of satellite random fault model with time 卫星随机故障模型在不同时间的可靠性如表5所示。利用动态故障树对卫星分系统进行建模分析,能够有效地得到各系统以及整星的随机故障发生概率,从而便于分析系统的薄弱环节,进一步提高卫星的可靠性。 最后,综合考虑卫星的损耗故障,将随机故障模型与损耗故障模型相乘得到卫星的可靠性模型,本文利用正态分布模型模拟卫星损耗故障[19],根据卫星寿命末期的要求,确定模型的期望为93 000,标准差为10 000,得到卫星的可靠性模型如图17所示。由图17可知,在卫星早期阶段,随机故障对卫星可靠性的影响较大,卫星可靠性随着时间的增大在缓慢下降,当卫星工作6×104h后,可靠性开始迅速下降,此时损耗累积的作用逐步显著,到达卫星寿命末期8.76×104h时,卫星的可靠性为0.59,此时损耗累积已成为影响卫星可靠性的主要因素,至工作时间105h时,卫星可靠性仅为0.2。 表5 卫星随机故障模型在不同时间的可靠性 图17 卫星可靠性模型Fig.17 Satellite reliability model 蒙特卡洛仿真是分析动态故障树的重要方法,其具有较高的计算精度,但计算时间较长,同时该方法也是评估其他方法的标杆。本文利用蒙特卡洛仿真方法对所得的卫星随机故障模型进行评估分析。仿真时,根据表4中底事件服从的寿命分布及参数,对各事件出现的时间进行抽样,将所得样本作为仿真时钟的推进点,并在推进点对系统进行评估和参数计算,直至系统失效或到达最大仿真时间,在仿真次数为105的条件下得到相应的可靠性曲线如图 18所示。 图18 基于蒙特卡洛仿真的可靠性曲线Fig.18 Reliability curve based on Monte Carlo simulation 在不同时间下,将本文方法与基于蒙特卡洛仿真方法进行对比,得到的计算结果如表6所示。结果表明,本文采取的动态故障树分析方法能够有效的分析卫星的随机故障,且所得的随机故障模型具有良好的精确性。 表6 本文方法与基于蒙特卡罗仿真方法对比 Weibull分布模型具有较强的适应性,能够拟合不同类型的数据,被广泛应用于系统可靠性的分析。本文在基于蒙特卡洛仿真所得到的可靠性数据的基础上,利用最大化拟合优度参数估计方法拟合得到Weibull分布模型。拟合优度表示拟合数据与模型之间的差异,其值越大则表明模型拟合度越好。基于蒙特卡洛仿真得到的可靠性拟合数据记为R(ti),Weibull分布模型的可靠性记为R′(ti,α,β),其中α为尺度参数,β为形状参数,则拟合优度R2可通过以下公式得到: (7) (8) (9) (10) 利用遗传算法对拟合优度函数进行优化,得到拟合优度的最大值,进而确定Weibull分布模型的参数。最终Weibull分布模型尺度参数α为295 742,形状参数β为1.46,拟合优度R2为0.999 3。 以基于蒙特卡洛仿真所得的可靠性数据为依据,将拟合得到的Weibull分布模型与本文所得的随机故障模型进行对比,计算两种模型与可靠性数据之间的残差绝对值,如图 19所示。由图 19可知,Weibull分布模型的残差绝对值的峰值基本上都大于本文所得的随机故障模型,并进一步求得残差绝对值的平均值,分别为0.001 2和0.000 7。 图19 两种模型与可靠性数据之间的残差绝对值Fig.19 Absolute value of residual between two models and reliability data 结果表明,基于动态故障树方法所得的随机故障模型能更好地贴合可靠性数据,更有效地模拟卫星部件随机故障的动态行为。 本文采用马尔可夫链和二元决策图相结合的动态故障树分析方法对卫星及3个分系统的动态逻辑和故障机制进行研究,建立完整的卫星动态故障树,得到卫星随机故障模型,并将随机故障模型和正态分布模型结合得到更为准确的卫星可靠性模型,解决了传统故障树分析方法无法描述卫星系统动态特性的问题。同时,该方法有利于分析系统的薄弱环节,进而提高卫星的可靠性。而后在蒙特卡洛仿真数据基础上对随机故障模型和Weibull分布模型进行评估比较,结果表明本文方法能更准确地反映卫星系统随机故障的动态行为,更利于卫星随机故障模型的建立和分析。

2.3 基于Markov的动态子树分析

2.4 结果分析



3 基于蒙特卡洛仿真的模型评估
4 Weibull分布模型比较
4.1 Weibull分布参数拟合
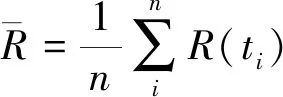
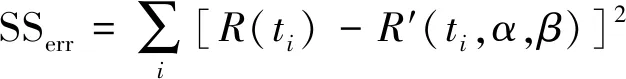
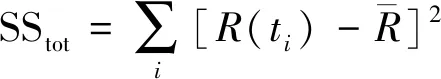
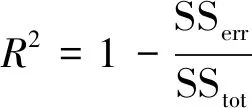
4.2 模型比较
5 结束语
