可变构型的控制力矩陀螺控制方法
2020-11-26张科备高晶敏关新郭子熙
张科备,高晶敏,关新,郭子熙
1. 北京控制工程研究所,北京 100190 2. 空间智能控制技术国防科技重点实验室,北京 100094 3. 北京信息科技大学 自动化学院,北京 100192
单框架控制力矩陀螺(control moment gyroscope, CMG)是卫星实现姿态敏捷机动的重要执行机构,在遥感类卫星姿态快速机动中得到广泛应用。在实际卫星姿态机动中,需要多个CMG进行三维力矩输出。因此,针对单框控制力矩陀螺群主要侧重于相关的操纵控制策略研究[1]。
针对控制力矩陀螺群固有的框架角奇异问题,多种性能良好的操纵方法应运而生。文献[2-3]针对CMG框架角奇异时无法提供三维力矩,提出一种释放奇异方向控制约束的降维控制方法,与鲁棒伪逆等操纵律相比,该方法能够快速高效逃离奇异。文献[4-5]针对鲁棒奇异规避操纵存在的框架“锁死”现象,设计了一种姿态控制力矩指令随奇异度量动态矢量调节的新型规避策略,在实现奇异规避的同时可有效避免卫星挠性振动激发。文献[6]针对CMG框架角奇异饱和问题,设计了一种零运动奇异规避动态分配与指令力矩随奇异度量相应调节的控制力矩陀螺操纵律,实现了CMG框架角速度去饱和快速脱离奇异问题。文献[7]详细分析了控制力矩陀螺操纵方法中的混合逆、广义逆、一般逆、奇异鲁棒逆[8]、一般奇异鲁棒逆[9]、奇异方向(singular direction avoidance, SDA)操纵律[10-11]、局部梯度操纵律、混合操纵律(hybrid steering logic, HSL)[12]等8种CMG操纵律,指出它们来源于一个共同的最优化指标函数,并且在最优化求解过程中都没有考虑奇异构型。其中前7种操纵律可以都源于同一个最优指标函数,各种操纵律的区别在于选择的权重系数不同。而混合操纵律HSL结合了奇异方向和局部梯度操纵律的优势。在双曲奇异时,HSL比SDA方法性能更好;在椭圆奇异时,HSL和SDA方法性能相当。HSL能够使CMG躲避椭圆奇异点,而且输出力矩误差较小。文献[13]针对五棱锥构型的CMG模型,设计了一种构型锥角可动态调整的奇异躲避的路径规划方法;该方法虽可有效提高特定机动方向的控制能力,但是需要设计复杂的安装结构,工程实现具有一定难度。文献[14]针对金字塔构型的CMG模型,设计了一种构型倾角可变的控制力矩陀螺操纵方法;与文献[13]相比,该方法仅通过安装基座的一个自由度控制实现多个CMG群的安装构型倾角改变,简化了安装构型设计的难度。文献[15]设计了一种增益调度操纵律,通过动态调节控制力矩陀螺的框架和转子力矩系数,实现了大力矩与精细力矩的“无缝”调配以及快速避奇异问题。文献[16-18]研究了不同构型下的CMG群奇异点分布,并设计了一种基于前馈和反馈的复合控制律,通过角动量管理,实现快速逃逸椭圆奇异点。
综上可知,现有研究中多侧重于CMG群固定构型 (如金字塔、五棱锥)下的操纵控制方法。而CMG群固定构型(安装构型倾角固定)存在以下不足:1)无法满足卫星多工况下(尤其是一定数目CMG故障工况)姿态敏捷机动任务需求。现有的固定安装构型倾角的CMG群,其最大合成角动量包络为近似球形,以满足航天器三轴均匀的控制能力需求。而航天器在轨姿态敏捷机动,往往对某个轴的敏捷机动具有较高要求,其余轴可放宽机动要求。这要求CMG群能够灵活改变自身的角动量包络。而当存在一定数目CMG故障时,现有的控制方法更加难以满足卫星姿态机动的需求。2)无法实现多自由度快速避奇异。单框架控制力矩陀螺具有严重的奇异问题,现有操纵控制方法仅能通过低速框架角一个自由度实现避奇异。
本文在分析CMG群合成角动量的基础上,引入安装构型倾角这一控制变量,设计了CMG群的低速框架转角、安装构型倾角、转子转速的多变量操纵律,实现了高性能力矩输出与快速避奇异,提高CMG群的使用效率。分析了金字塔构型下不同数目CMG故障情况下的角动量包络。结合卫星姿态快速机动进行数学仿真校验,验证不同数目下的CMG群控制能力。
1 动力学描述
如图1所示,4个CMG组成金字塔构型系统,令安装构型倾角为β,可获得卫星本体下三轴对称的角动量包络。在卫星本体下,其合成角动量可表示为:

(1)
式中:δi为第i个CMG的框架角,i=1,2,3,4;cβ=cosβ,sβ=sinβ,cδi=cosδ,sδi=sinδi,hi=IswiΩi,为第i个CMG的标称角动量,Iswi为第i个CMG高速转子惯量,Ωi为第i个CMG高速转子转速。
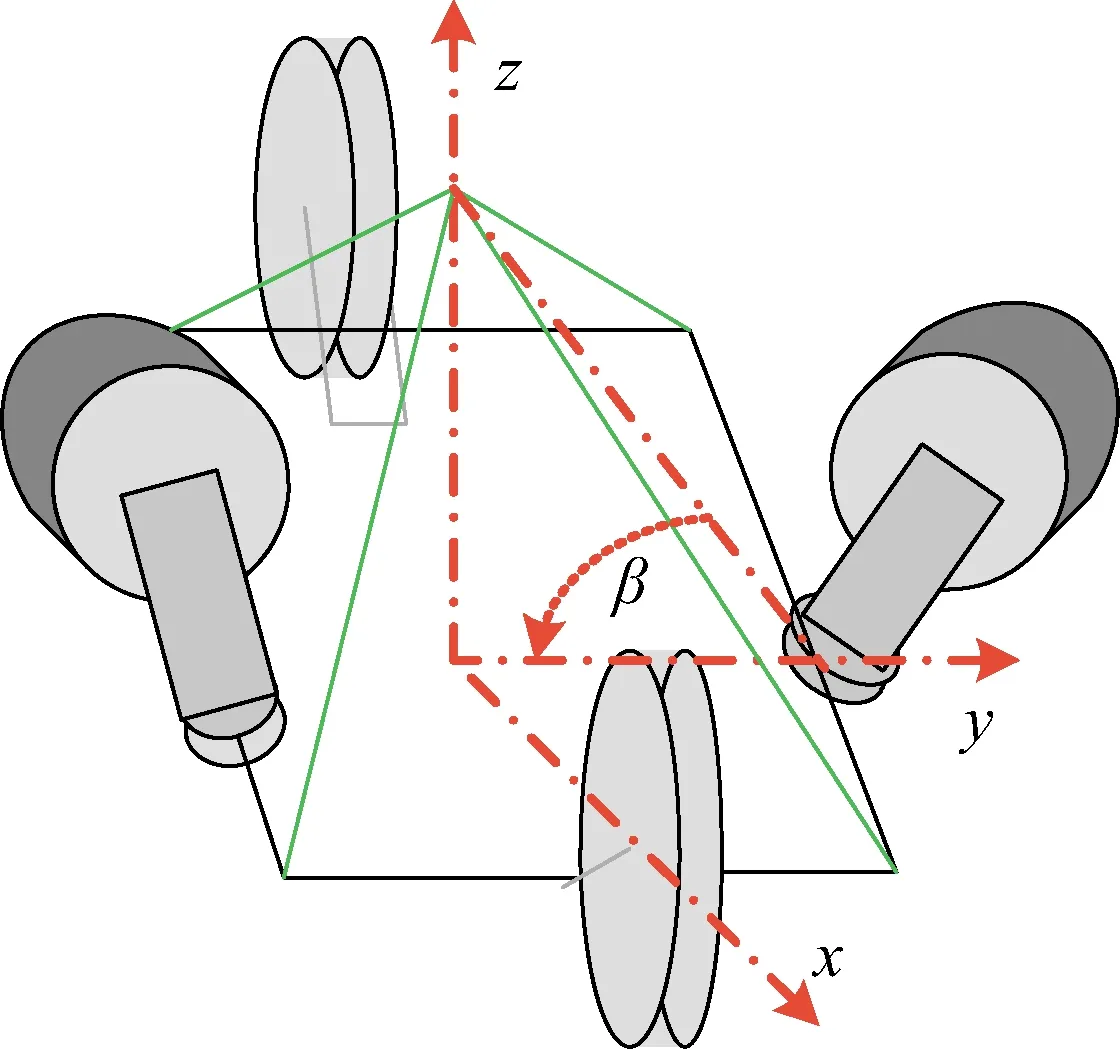
图1 金字塔构型CMG群Fig.1 Pyramid-type CMG system
若CMG群的安装构型倾角β可控,由式(1)可知,CMG群合成角动量与框架角δi、高速转子转速Ωi以及安装构型倾角β相关。因此,综合考虑δi、Ωi、β等多变量因素,求取式(1)合成角动量对时间的导数。在卫星本体系下,CMG群输出合成力矩τ可表示为:
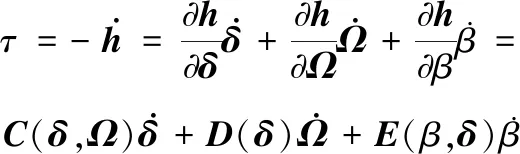
(2)
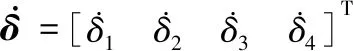
2 操纵控制设计
2.1 动态权重分配的指令操纵控制
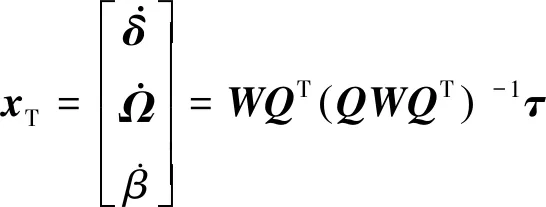
(3)
式中:Q=[C,D,E];W=diag(Wg1, …,Wg4,Ws1, …,Ws4,Wβ)为CMG群框架角、高速转子、安装构型倾角三者之间力矩的权重分配矩阵,Wgi=Wg0exp(-εK1)为第i个CMG的框架角力矩权重系数,其中Wg0,ε为设计参数,K1为CMG群框架角奇异度量[8],Wsi为第i个CMG高速转子的权重系数,Wβ为安装构型倾角力矩权重系数。
采用高斯函数计算式(3)中的框架角速度力矩权重系数Wg0和高速转子力矩的权重系数Wsi这两个力矩分配系数。定义高斯函数为f(x,a,b,c)=a×exp[-(x-b)2/ (2c2)]。则设计Wg0和Wsi这两个力矩分配系数为

(4)
其中参数Wg00,Wg01,Ws0i,Ws1i,ag0,as0,bg0,bs0,cg0,cs0为设计参数。
上述设计的操纵律,通过判断整星姿态控制的目标力矩的模x=norm(τ)动态调节各个量的力矩分配系数。当姿态控制力矩的模norm(τ)远离0时,通过式(4)计算,平滑调大框架角力矩权重系数Wg0以及安装构型倾角力矩分配系数Wβ,通过改变框架转角速度和安装构型,进行大力矩输出;当姿态控制力矩的模norm(τ)接近0时,通过式(4)计算,操纵律平滑调小Wg0和Wβ,调大高速转子的权重系数Wsi。此时,CMG群框架角分配力矩接近于0,保持稳定,避免了框架转动输出较大的扰动力矩;安装构型倾角分配力矩接近于0,CMG群保持稳定的构型。通过高速转子改变转速,输出精细力矩,实现卫星的高精度高稳态控制。式(4)选取适当的参数,则可计算出Wg0、Wsi和Wβ力矩分配系数,如图2所示。
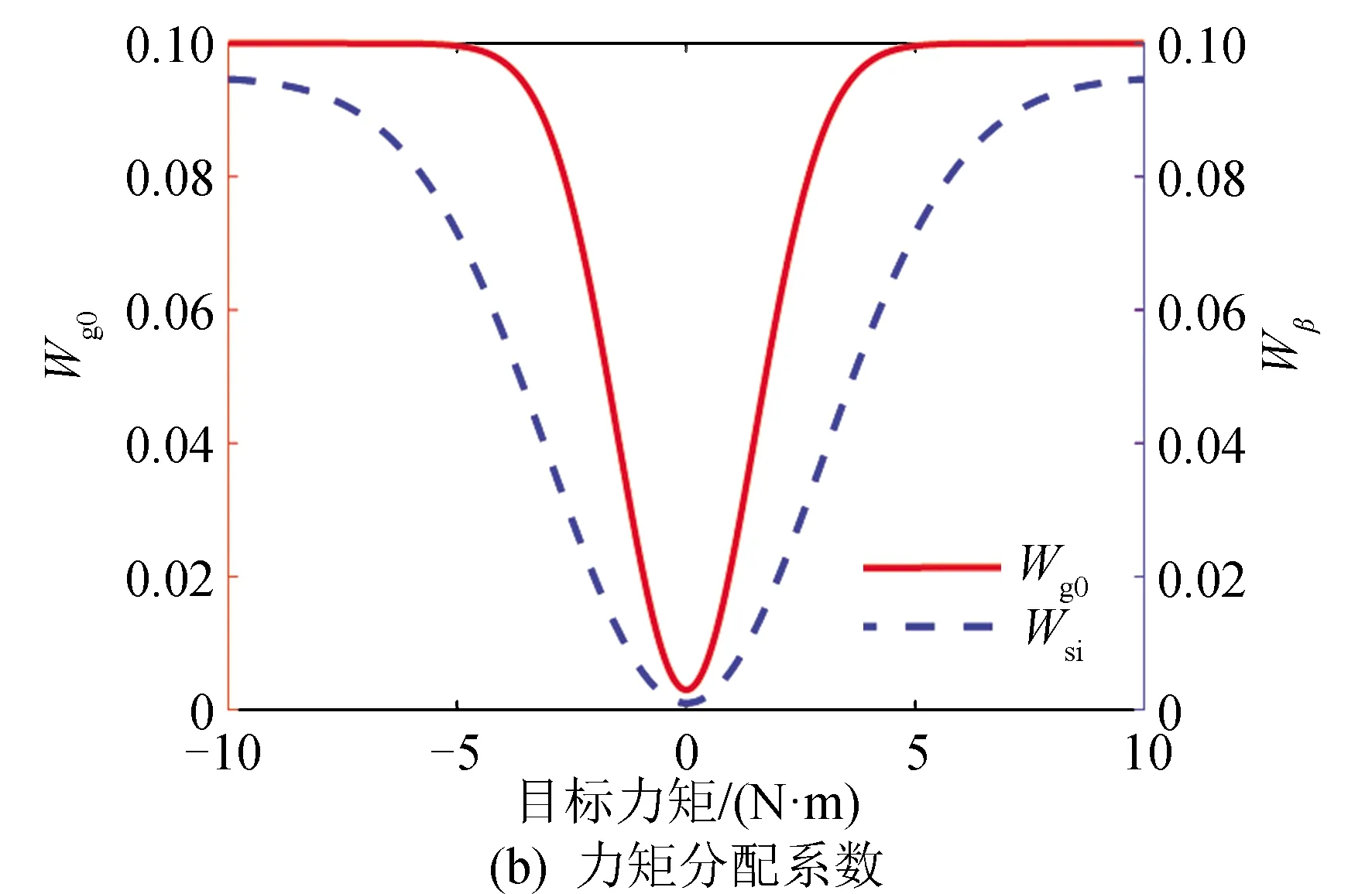
图2 力矩分配系数Fig.2 Torque distribution coefficient
2.2 零运动避奇异操纵控制
CMG群零运动避奇异操纵律是实现CMG群在整个工作空间无奇异操作的必要方法。当CMG群框架角接近奇异或者进入奇异状态时,且CMG群的安装构型倾角β可控时,可通过CMG群框架角δ和安装构型倾角β进行多自由度快速脱离奇异。其中,采用CMG群框架角δ进行避奇异的零运动操纵律可表示为[19]:
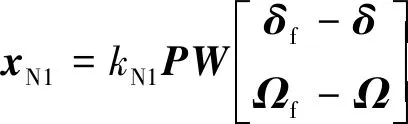
(5)
式中:kN1为零运动操纵律系数;P=I8-WQT(QWQT)-1为零运动正交投影矩阵;δf为CMG群期望框架角;Ωf为CMG期望的转子转速。
通过CMG群框架角δ和安装构型倾角β共同运动避奇异的零运动操纵律为:
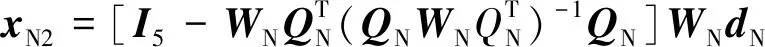
(6)
式中:QN=[C,E];WN为零运动避奇异时框架角和安装构型倾角力矩系数分配;dN为框架角、安装构型倾角零运动的矢量,具体表示为:
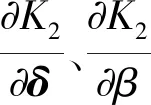
综上,在CMG群指令操纵律式(4)的基础上,通过添加式(5)(6)的零运动操纵律,进行避奇异和转子转速平衡。则CMG群的总的操纵律为:
x=xT+xN1+xN2
(7)
3 角动量包络与奇异性分析
采用奇异可视化方法分析安装构型倾角β可控时,CMG群角动量包络面及奇异点分布情况。当CMG群框架在奇异状态下,对应奇异方向矢量us=[ux、uy、uz]的奇异角动量hs=[hsx、hsy、hsz]可以表示为[16]:

(8)

通过式(8)可计算出CMG群内部奇异角动量的解析表达式,具体为[14]:
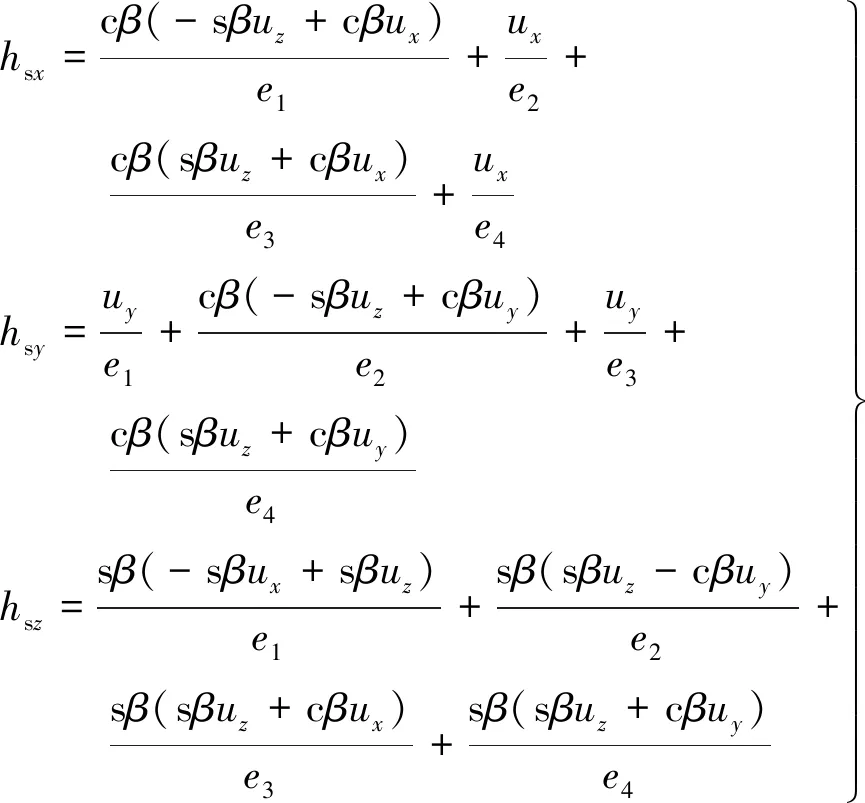
(9)
式中:e1、e2、e3、e4可表示为:
当安装构型倾角可变化的情况下,对式(9)求导,可得到在构型倾角可变化情况下的奇异度面。其型倾角可变化时内部奇异面hk=[hkx、hky、hkz]可以表示为:

(10)
金字塔构型是CMG群构型中奇异程度表现最严重的一种构型,考虑4个CMG组成金字塔构型,分析其角动量包络面以及奇异面。设置单个CMG的标称角动量为hi=70 N·m·s。设置安装构型倾角β的变化范围为0°~50°,通过计算得到安装构型倾角可变化情况下的CMG群的最大角动量包络面;图3给出了不同固定倾角与倾角可控的角动量包络对比。图3(a)给出倾角β=50°的CMGs群能够实现三轴近似对称的角动量包络,XOY平面内的角动量较大,YOZ平面内Z轴方向角动量包络较小。图3(b)给出倾角β=2°的CMGs群角动量包络,YOZ平面内Z轴方向角动量包络较大,但是XOY平面内的角动量难以进一步提高。分析图3(a)~(c)可知,相对于固定倾角的角动量包络仅能实现某个方向的角动量最优,倾角可变的角动量包络能够实现三维方向的角动量包络最大化,能够最大化地发挥CMG群的角动量优势,为航天器姿态快速机动提供更多的角动量。图3(d)~(e)给出了不同工况下角动量包络在YOZ平面和XOY平面的投影对比。以航天器本体系YOZ平面中Z轴为例,通过改变倾角,CMG群合成角动量由180 N·m·s提高到280 N·m·s左右(见图3(d)),提高了航天器Z轴方向的敏捷机动能力。航天器在本体系XOY平面内机动时,相对于固定倾角的角动量包络(如倾角β=2°),倾角可变的角动量包络能够实现XOY平面内的角动量包络最大化,为航天器滚动-俯仰姿态快速机动提供更多的角动量。通过改变倾角,CMG群合成角动量由158 N·m·s提高到247 N·m·s左右,提高了航天器在XOY平面内的敏捷机动能力(见图3(e))。
在金字塔构型的CMG群中,当存在某个或某几个CMG故障时,通过改变安装构型倾角β依然能够实现整个CMG系统具备最大范围的角动量包络。图4给出了不同CMG故障时的角动量包络。分析图4可知,当CMG存在1个(见图4(a))或2个(见图4(c))故障时,固定倾角的角动量包络(倾角β=50°)范围与图3(a)相比明显减小,CMG群敏捷机动能力下降。倾角可变的角动量包络(见图4(b)(d))依然能够实现较大范围的三维方向的角动量包络,依然能够为航天器姿态快速机动提供较多的角动量。


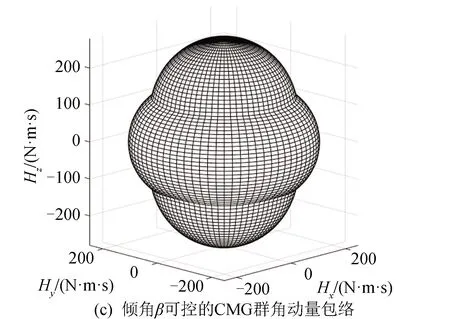
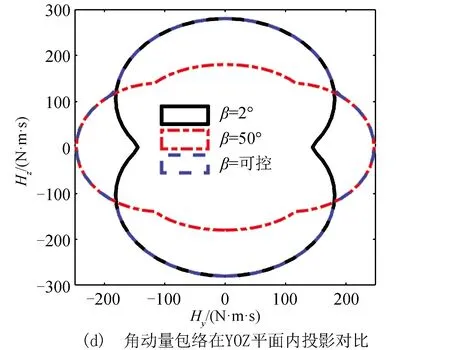

图3 CMG群角动量包络对比Fig.3 Comparison of angular momentum envelop for CMGs
通过式(9)可求在金字塔构型奇异矢量us对应的奇异角动量包络、显奇异点等的分布图。图5给出了固定倾角(β=50°)与倾角可变的显奇异点在XOY平面内投影对比。通过分析可知,相对于固定倾角的显奇异点而言,倾角可变的CMG群内部无奇异点范围更大,能够提供XOY平面更大能力的无奇异操纵。

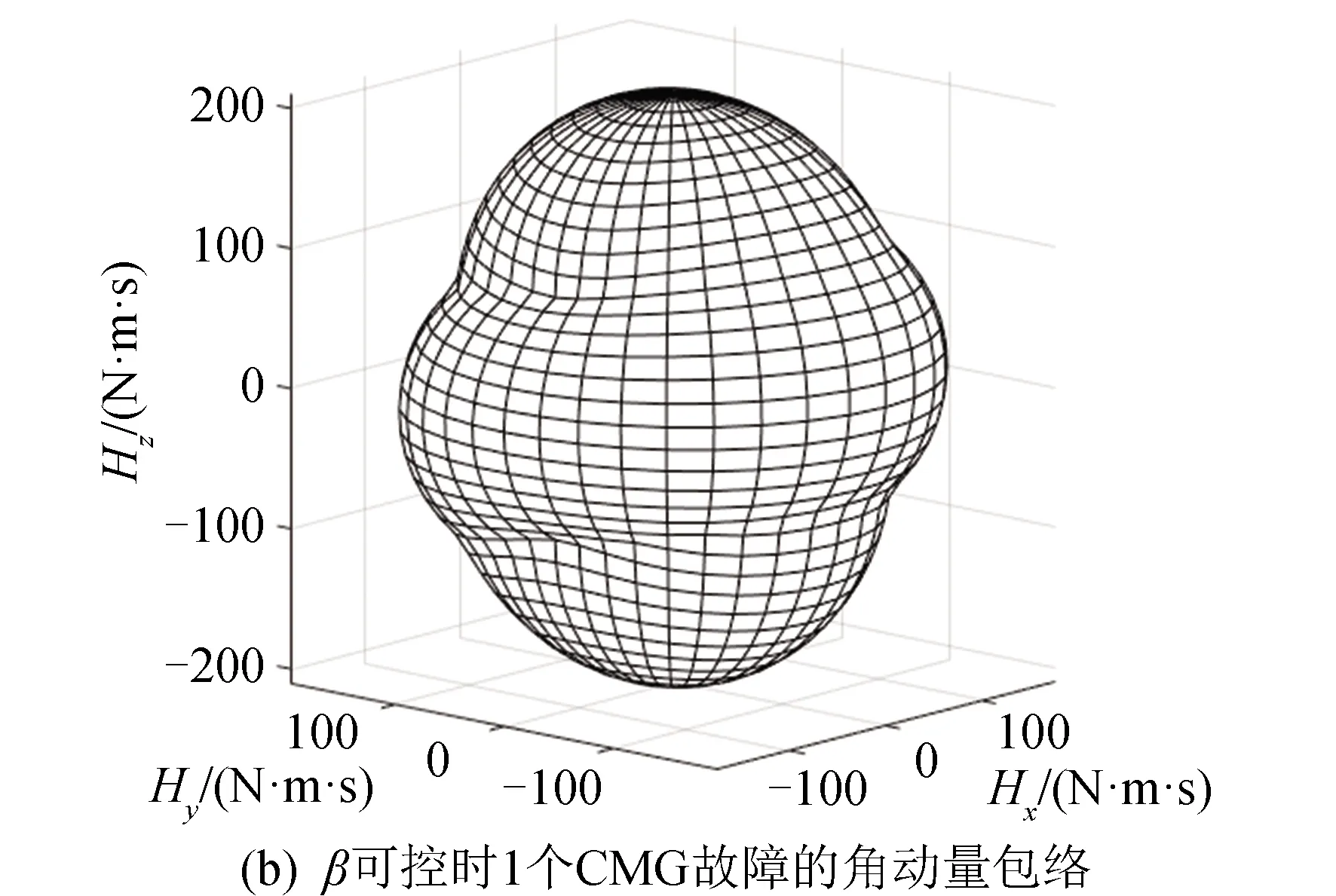
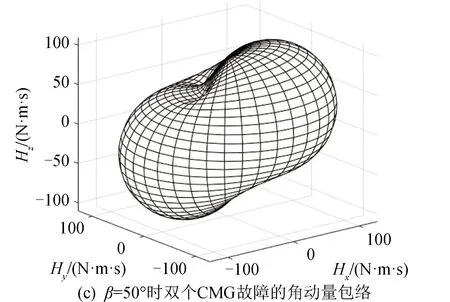
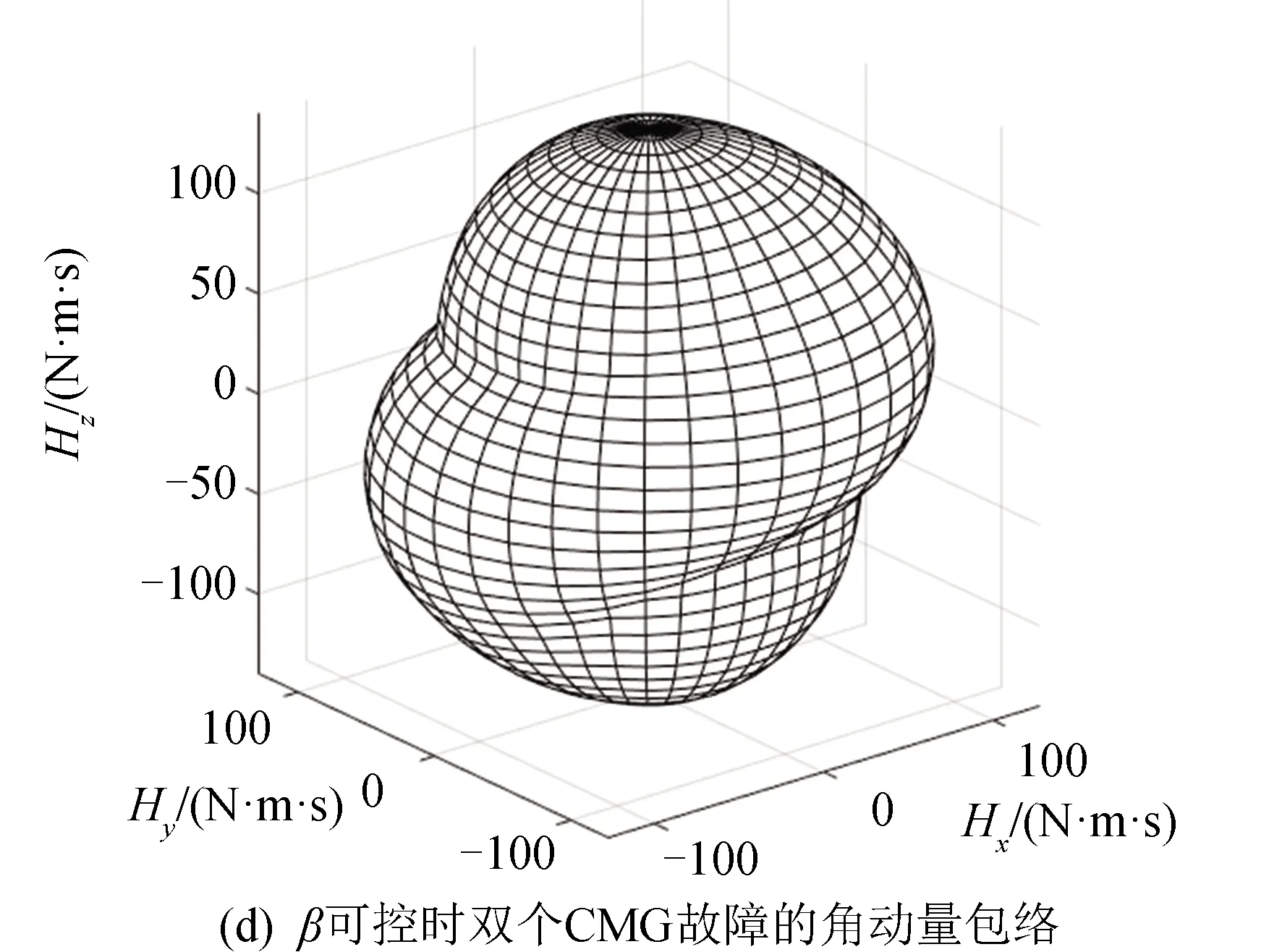
图4 不同CMG故障的角动量包络对比Fig.4 Angular momentum envelop for different CMG faults


图5 奇异点分布对比Fig.5 Comparison of singularity
4 数学仿真校验
进行卫星姿态机动数学仿真,校验CMG群操纵控制方法的有效性。星体转动惯量为J=diag(1 608, 1 608, 2 010)kg·m2、4个CMG采用金字塔构型安装,每个CMG标称角动量为70 N·m,高速转子标称转速为628.32 rad/s,CMG框架最大角速度为1 rad/s。卫星初始姿态为[30,10, -30] °,目标姿态为[0,0, 0] °。
(1)算例1
设置卫星姿态机动最大角加速度amax=2.0(°)/s2,最大角速度ωmax=5.0(°)/s;指令操纵律的相关系数为,Wg0=0.1,Wsi=40,kN1=0.2;设置安装倾角β力矩系数Wβ由0.000 1~0.1之内变化,测试在相同敏捷机动情况下,不同力矩系数Wβ对框架角速度的影响。
算例1仿真结果如图6~图9所示。图6给出了卫星敏捷机动过程中的姿态和角速度曲线,在整个过程中采用可变构型的控制力矩陀螺控制方法能够实现卫星的三轴姿态敏捷机动。图7给出了不同安装倾角β力矩系数Wβ下的CMG框架角速度对比。当Wβ=0.000 1时,此时安装倾角基本无变化,主要依靠CMG群的框架转动输出力矩。如图7(a)所示,此时4号CMG框架角速度幅值接近饱和,1号、3号CMG框架角速度幅值在44(°)/s左右。当Wβ=0.1时,通过安装倾角变化和框架转动输出力矩。如图7(b)所示,此时CMG框架角速度最大幅值在42(°)/s左右。通过安装倾角变化降低了卫星姿态敏捷机动过程对框架转角转速的要求。图8给出了4种安装倾角力矩系数下的安装倾角β变化率对比结果。安装倾角β最大变化速率小于6(°)/s。图9给出了4种安装倾角力矩系数下的框架角奇异度量K1的对比结果。通过安装倾角变化提高了CMG群的奇异度量,这表明在相同奇异度下,CMG群具有更大的力矩输出能力。
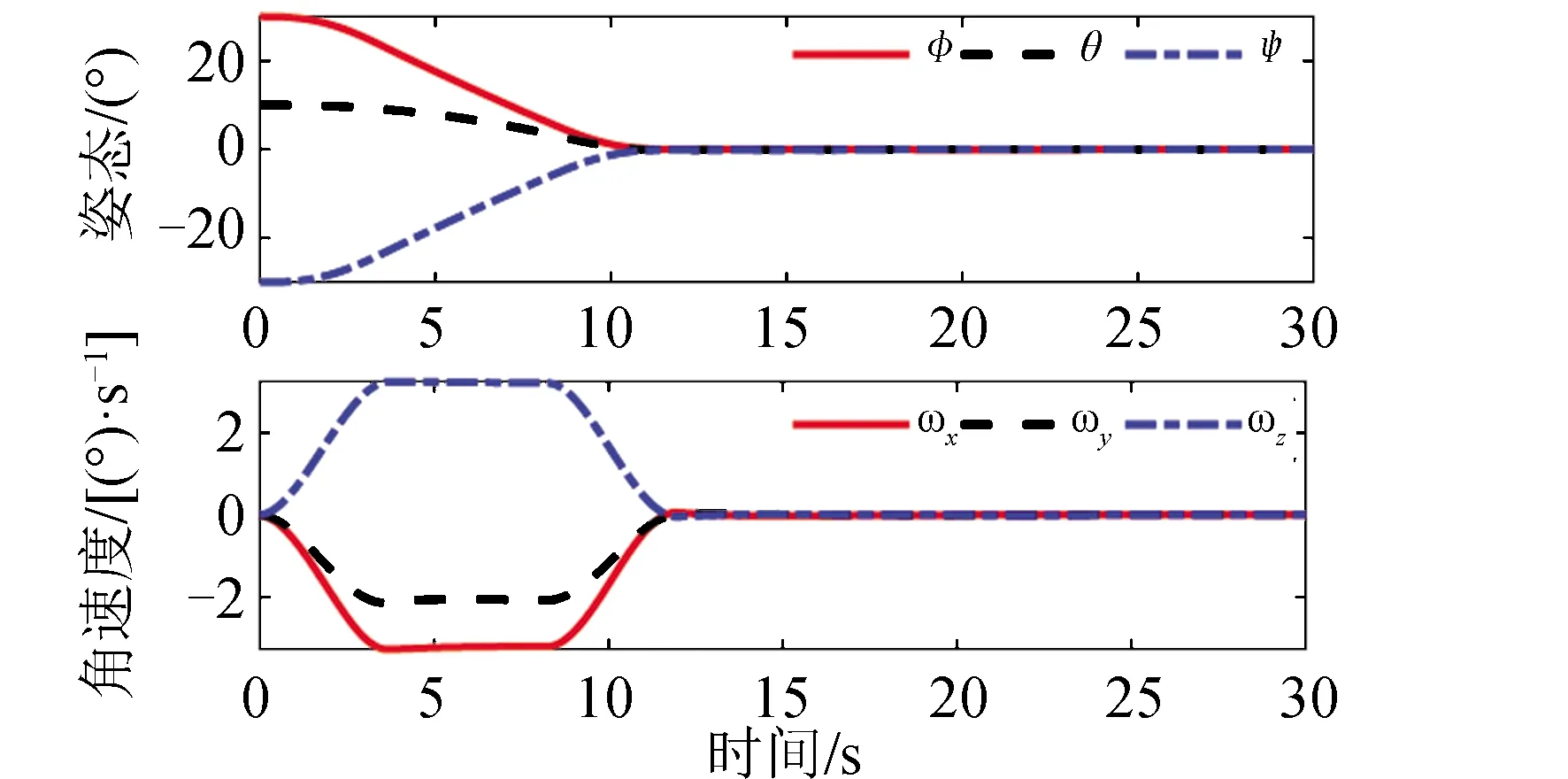
图6 卫星敏捷机动姿态和角速度Fig.6 Attitude and rate for satellite

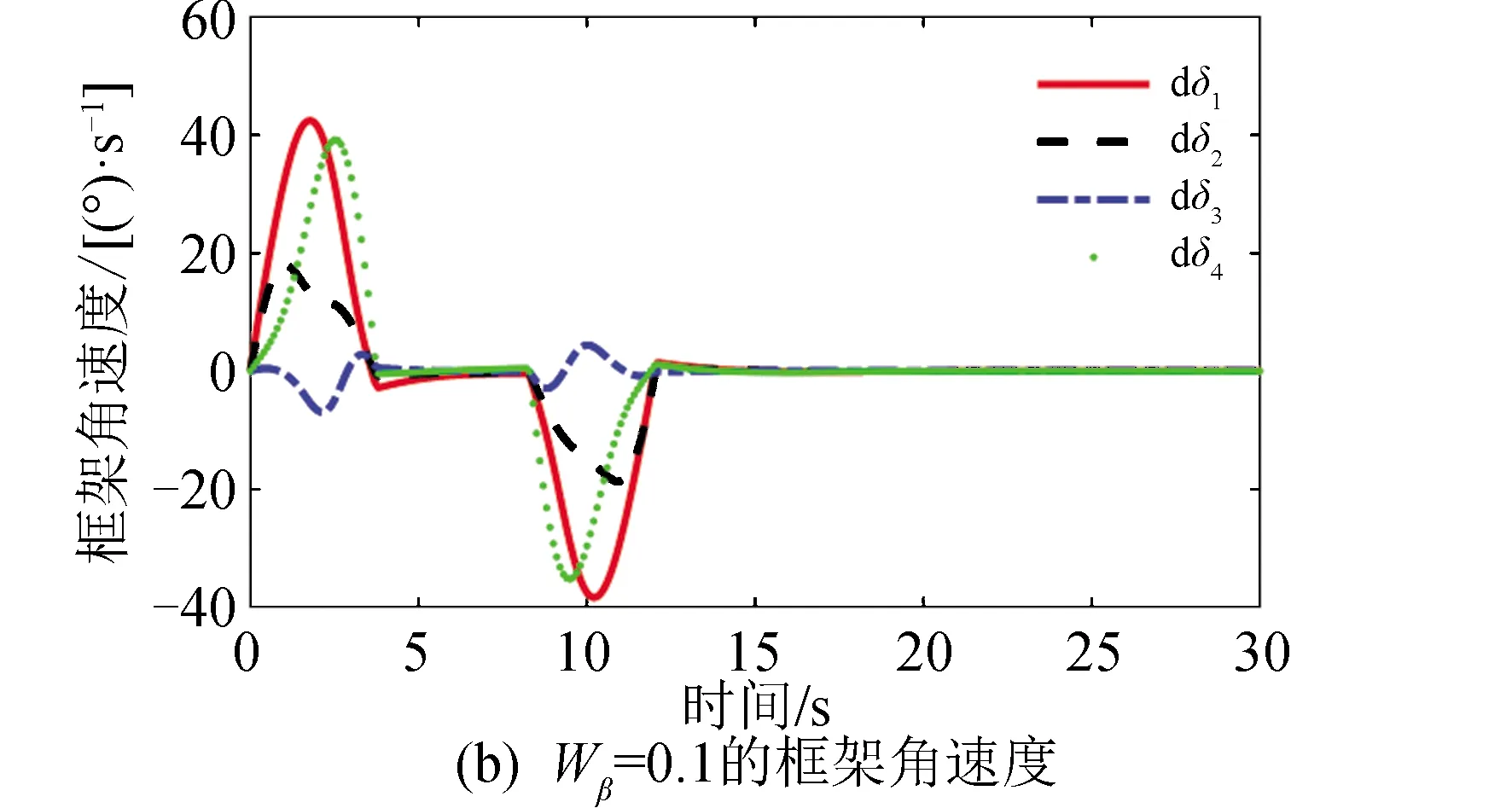
图7 CMG群框架角速度对比Fig.7 Comparison of CMGs gimble rate
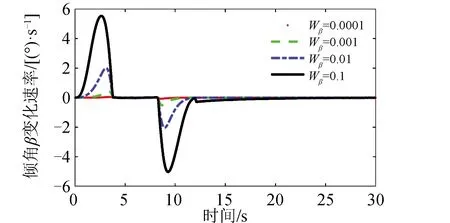
图8 安装倾角β变化速率对比Fig.8 Comparison of skew angle β rate

图9 奇异度对比Fig.9 Comparison of CMGs singularity
(2)算例2
设置4号CMG故障,验证金字塔构型下3个CMG进行卫星姿态机动控制的能力。姿态机动最大角加速度amax=1.0(°)/s2,最大角速度ωmax=1.6(°)/s;安装倾角β力矩系数Wβ=0.1。
算例2的仿真结果如图10~图12所示。图10给出了采用3个CMG控制下的卫星敏捷机动姿态和角速度曲线,在整个过程中采用可变构型的控制力矩陀螺控制方法能够实现卫星的三轴姿态敏捷机动。图11给出了采用3个CMG进行姿态控制的框架角速度。1号CMG框架角速度幅值在28.4(°)/s左右。2号、3号CMG框架角速度幅值在10(°)/s左右。图12给出了安装倾角β及其变化速率。在整个姿态控制期间安装倾角β最大变化速率小于3.6(°)/s。
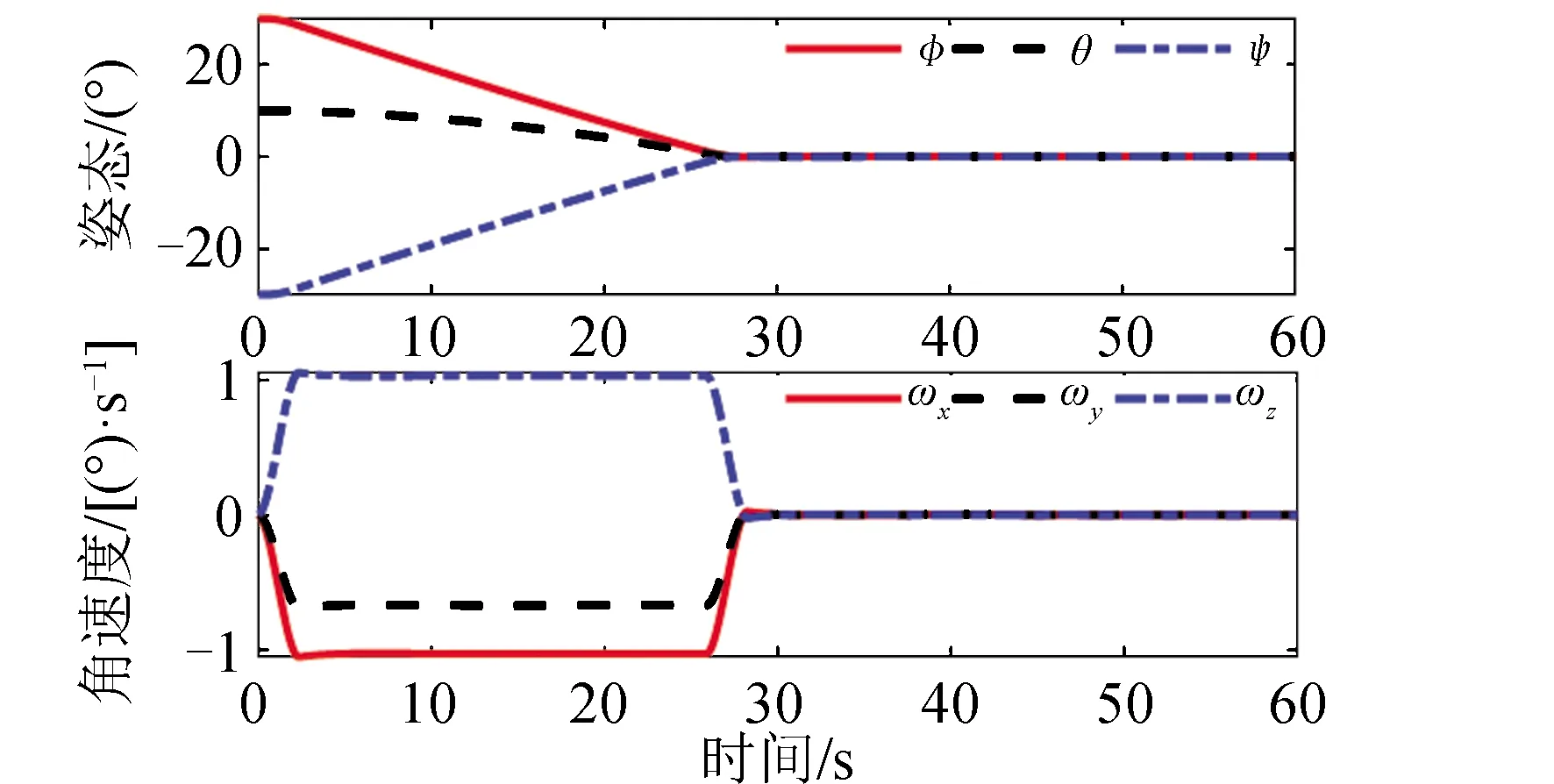
图10 3个CMG控制的卫星姿态和角速度Fig.10 Satellite attitude and rate for three CMGs used
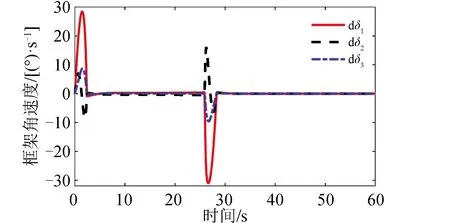
图11 3个CMG控制的框架角速度Fig.11 Gimble rate for three CMGs used
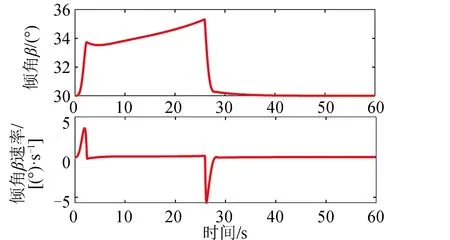
图12 3个CMG控制的安装倾角β和变化速率Fig.12 Skew angle β and rate for three CMGs used
(3)算例3
设置3号、4号CMG故障,验证金字塔构型下2个CMG进行卫星姿态敏捷机动控制能力。姿态机动最大角加速度amax=1.0(°)/s2,最大角速度ωmax=1.6(°)/s;安装倾角β力矩系数Wβ=0.1。
算例3的仿真结果如图13~图14所示。图13给出了采用2个CMG进行姿态控制的框架角速度。1号CMG框架角速度幅值在21.8(°)/s左右。2号CMG框架角速度幅值在10(°)/s左右。图14给安装倾角β及其变化速率。在整个姿态控制期间安装倾角β最大变化速率小于13.9(°)/s。

图13 2个CMG控制的框架角速度Fig.13 Gimble rate for two CMGs used
分析图11~图14可知,在采用2个CMG进行姿态敏捷控制时,CMG群框架角速度稍有减少,但是通过安装倾角β的变化亦能输出三维力矩,实现卫星的三轴姿态控制。
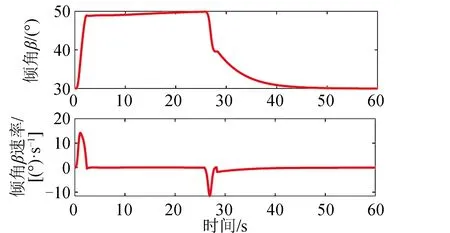
图14 2个CMG控制的安装倾角β和变化速率Fig.14 Skew angle β and rate for two CMGs used
5 结束语
文中设计了一种可变构型的控制力矩陀螺控制方法,提升了控制力矩陀螺群角动量输出能力,实现航天器敏捷机动能力的进一步提升。具体为:
1)通过改变控制力矩陀螺群安装构型倾角β,实现了金字塔构型下,YOZ平面中Z轴的CMG群合成角动量由180 N·m·s提高到280 N·m·s,使航天器Z轴敏捷机动能力提升约55%。
2)设计了CMG框架角δi、高速转子转速Ωi以及安装构型倾角β等多变量避奇异操纵律,实现了在金字塔构型下,XOY平面内CMG无奇异操纵角动量范围由110 N·m·s扩大到150 N·m·s左右,使CMG无奇异操纵范围提升36%左右。
3)在金字塔构型下,存在CMG故障时,现有的CMG操纵律实现航天器三轴敏捷机动面临诸多约束,文中设计的可变构型的控制力矩陀螺控制方法,实现了不同数目CMG故障下的卫星三轴敏捷机动控制,满足不同工况下的姿态机动需求,具有更强的鲁棒性。
为使本文提出的方法能够在实际应用得到推广,仍需要进一步分析驱动构型倾角β变化的执行机构能力以及各个CMG的角动量变化对执行机构的反作用影响。
