整体箱板式高桩码头地震响应数值模拟分析
2020-11-25庄宁许明宇陈聪杨文涛
庄宁 ,许明宇 ,陈聪 ,杨文涛
(1.河海大学港口海岸与近海工程学院,江苏 南京 210098;2.河海大学水利工程实验教学中心,江苏 南京 210098)
0 引言
高桩码头是我国应用最广的码头结构形式之一,地震作用下高桩码头的破坏形式主要有两种[1]:一是桩基在土分界处桩身曲率过大,桩基发生破坏;二是土体液化,使码头整体失稳从而导致破坏。传统带斜桩式高桩码头较弱的抗震性能限制了码头自身的发展,新型高桩码头结构的抗震问题成为防灾减灾研究中的一项重要课题[2]。整体箱板式高桩码头上部结构由数块预制箱板拼接而成,通过纵向预应力筋穿过箱板预留孔洞将箱板结合成一个整体,且不需设置斜桩,该新型全直桩码头结构可以承受较大的水平荷载,同时在地震作用下较之斜桩码头更不易被破坏,抗震性能大大增强。
邴晓等[3]首次提出新型整体箱板式高桩码头的结构形式,从施工、工程量和经济指标等方面论证了这种新型码头设计优于传统的梁板式高桩码头。王文仲等[4]验证了经验系数法、等代框架法、虚拟交叉梁法应用在整体箱板式高桩码头中的可行性,并与有限元数值计算结果对比。张舰[5]利用ABAQUS准确模拟了整体箱板式高桩码头桩基内力和门机荷载的动态加载,验证了数值模拟在新型码头中的可行性。
目前针对地震影响下的整体箱板式高桩码头结构的研究很少,本文采用数值模拟的研究方法,利用有限元软件ABAQUS建立基于实际工程条件下的弹塑性损伤数值模型,采用无限元模拟实际的边界条件,考虑材料非线性和桩土相互作用,分析结构在不同地震波强度作用下的动力响应,进一步深化整体箱板式高桩码头结构抗震性能的研究。
1 计算模型建立
本文模型数据参考某港区5万吨级整体箱板式高桩码头结构设计[6],选用ABAQUS中提供的混凝土塑性损伤模型,土体材料选用摩尔库伦本构模型[7-8],将土体简化为2层,分别为淤泥质粉质黏土和砂质板岩。混凝土等级为C50,地震设防烈度为8度。塑性系统松弛时间黏性系数取为1×10-5,混凝土双轴受压与单轴受压极限强度比值取1.16。此外,P-Q平面剪胀角取38°,塑性势能方程的流动势偏移量取0.1,拉伸子午线和压缩子午线上第二应力不变量比值取2/3。上部结构中双层纵向预应力筋在箱板横断面上下各布置62根,并对每根钢筋施加1.3×109Pa的预应力。码头断面图和码头平面图如图1、图2所示(每榀排架的桩基编号从海侧向陆侧依次为1~4号,如2-3表示第2榀排架的3号桩基),码头尺寸为码头宽度35 m,排架间距7.28 m,箱板厚度1.65 m,1、2号桩截面(单根桩)1.2 m×1.2 m,3、4号桩截面(两根桩)1 m×1 m,桩长57.95 m。土层物理力学性能指标见表1。

图1 码头断面图(m)Fig.1 Cross-sectional view of wharf(m)

图2 码头平面图(mm)Fig.2 Plan view of wharf(mm)
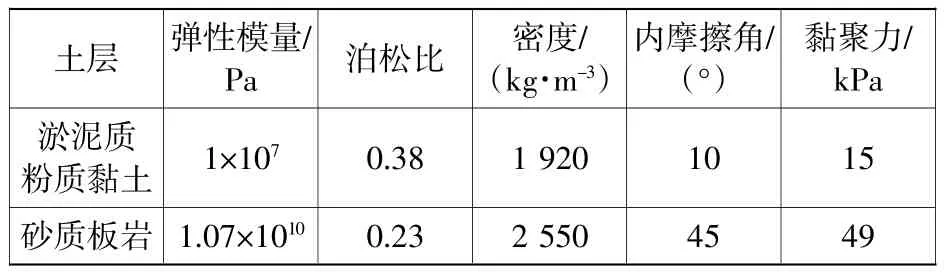
表1 土层物理力学性能指标Table1 Physico-mechanical properties of soil layer
本文借鉴以往研究者[9]的研究方法,利用过去的典型地震波记录进行地震分析,分别选择频谱特征不同的EIcentro波、Northridge波和Kobe波作为输入地震波,纵向施加,持续时间为15 s。根据抗震设防烈度的要求[10],将地震波加速度峰值调整为0.1g、0.2g、0.4g,对应的抗震设防烈度为7度、8度、9度地震。
模型中码头结构与土体均采用ABAQUS中的三维实体C3D8R单元[11],预应力钢筋采用B31线单元,无限元部分采用CIN3D8单元。对于阻尼计算,采用黏性阻尼模型[12-13]中的瑞利阻尼进行计算。除了土体上表面(Y向正方向)为自由面外,其余5个方向的表面作为不反射地震波的无穷远表面,在考虑地应力平衡的条件下[14],最终生成有限元与无限元耦合的整体箱板式高桩码头结构模型。
2 面板动力响应分析
2.1 面板位移响应
分别调整加速度峰值为0.1g、0.2g、0.4g的EIcentro波和0.2g的Northridge波、Kobe波作为输入地震波,面板水平位移时程曲线分别如图3和图4所示(位移正向为向海侧方向)。
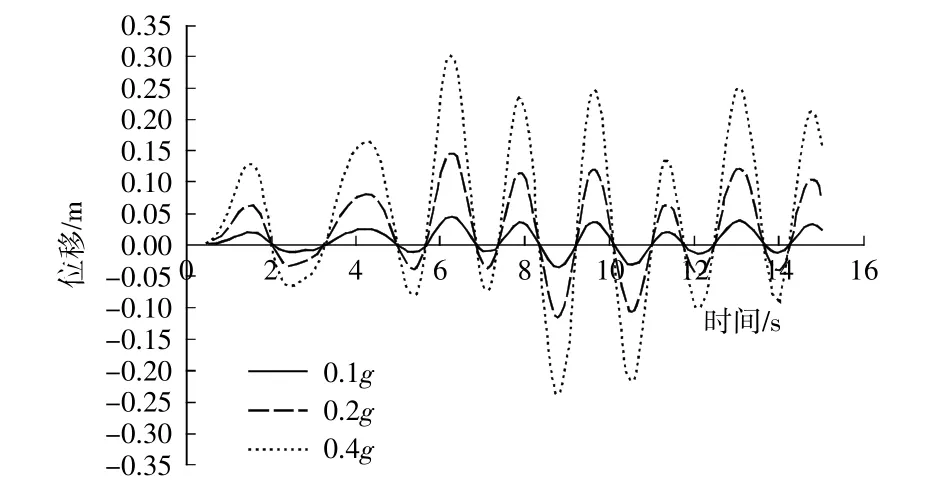
图3 不同强度EIcentro波作用下码头面板水平位移时程曲线Fig.3 Time-history curveof horizontal displacement of panel under EIcentro waves with different strength
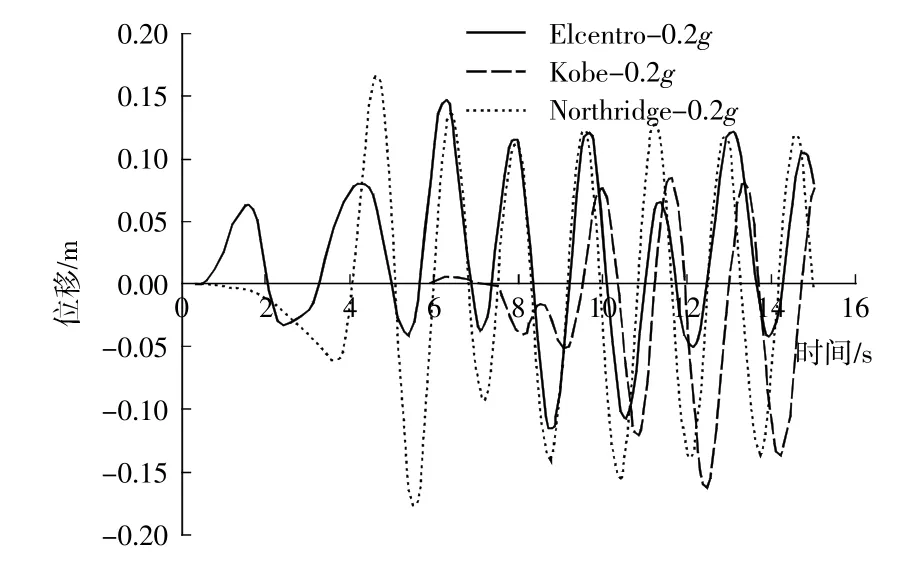
图4 不同地震波作用下码头面板水平位移时程曲线Fig.4 Time-history curve of horizontal displacement of panel under different seismic waves
由图3可知,面板水平位移与加速度趋势基本匹配,结构受到向海侧加速度时位移幅值更大,结构响应更加明显。随着地震波强度的增大,面板的水平位移响应也逐渐增大,残余位移就越明显。在0.4g(9级)地震强度下,码头面存在明显的向海侧偏移的情况,位移达到最大,结构响应强烈,结构发生不可恢复的塑性破坏。
由图4可以看到,对比EIcentro波和Kobe波,EIcentro波作用下面板最大正向位移更大,面板向海侧偏移更大,而Kobe波作用下面板最大负向位移更大,面板向陆侧偏移更大。在Northridge波作用下面板水平位移变化幅值最大,表明面板在该地震波下响应最为剧烈。
2.2 面板加速度响应
不同强度的地震波作用下面板水平加速度时程曲线分别如图5~图6所示。
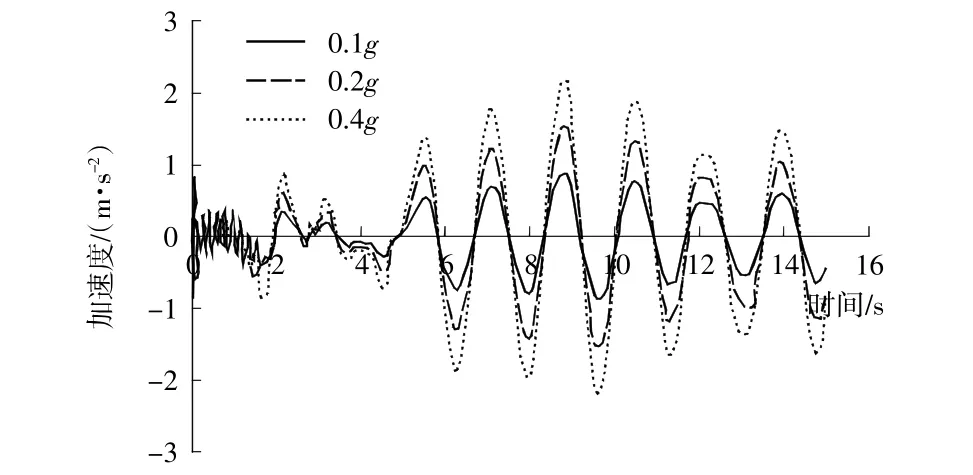
图5 不同强度EIcentro波作用下码头面板水平加速度时程曲线Fig.5 Time-history curve of horizontal acceleration of panel under EIcentro waveswith different strength
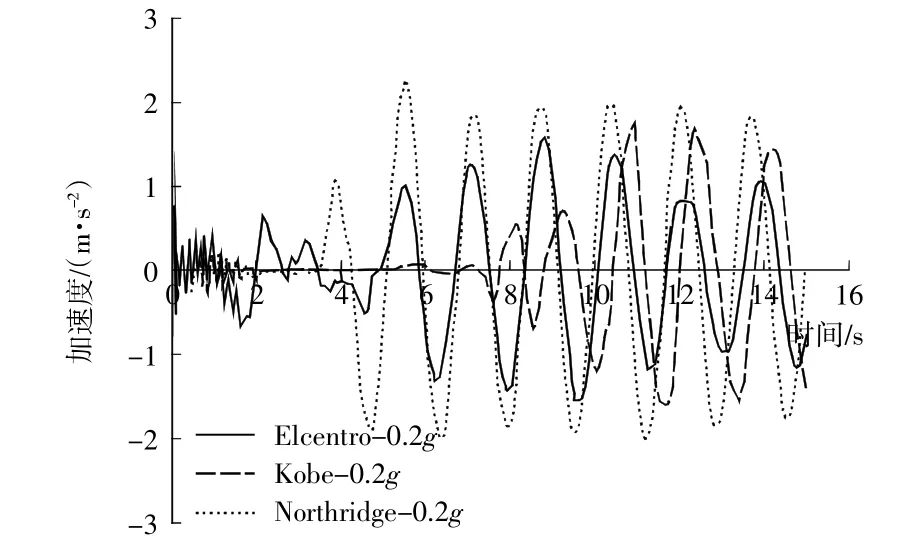
图6 不同地震波作用下码头面板水平加速度时程曲线Fig.6 Time-history curve of horizontal acceleration of panel under different seismic waves
由图5可知,面板水平加速度在不同地震波强度下的时程曲线表现出相似的变化规律,随着地震波强度的增大,水平加速度峰值也随之增大。不同强度下加速度峰值都有所衰减,且地震波强度越大,衰减幅度就越大,这是因为地震波从岩基传播到面板过程中会发生能量的消耗,面板混凝土采用的损伤模型引入了损伤参数,结构在强震下会发生损伤劣化,刚度降低。
由图6可知,3种地震波的水平加速度时程曲线与各自对应的输入地震波加速度时程曲线相似,但三者在线形规律以及峰值变化上存在较大差异。EIcentro波和Kobe波的峰值加速度与其对应的输入地震波相比都有所衰减,而Northridge波却有所增强,加速度峰值呈增长趋势,这是因为Northridge波振动能量集中在0.1~0.8 Hz及2.0~2.6 Hz,并且结构本身的自振频率(0.196~0.355 Hz)恰好在这之间,使结构发生共振,响应更为剧烈。
3 桩基动力响应分析
选取结构第一榀排架的桩基作为研究对象,其编号从海侧向陆侧依次为1-1~1-4。
3.1 桩身位移响应
不同强度的地震波作用下1-1桩身各点的水平位移峰值曲线如图7所示。
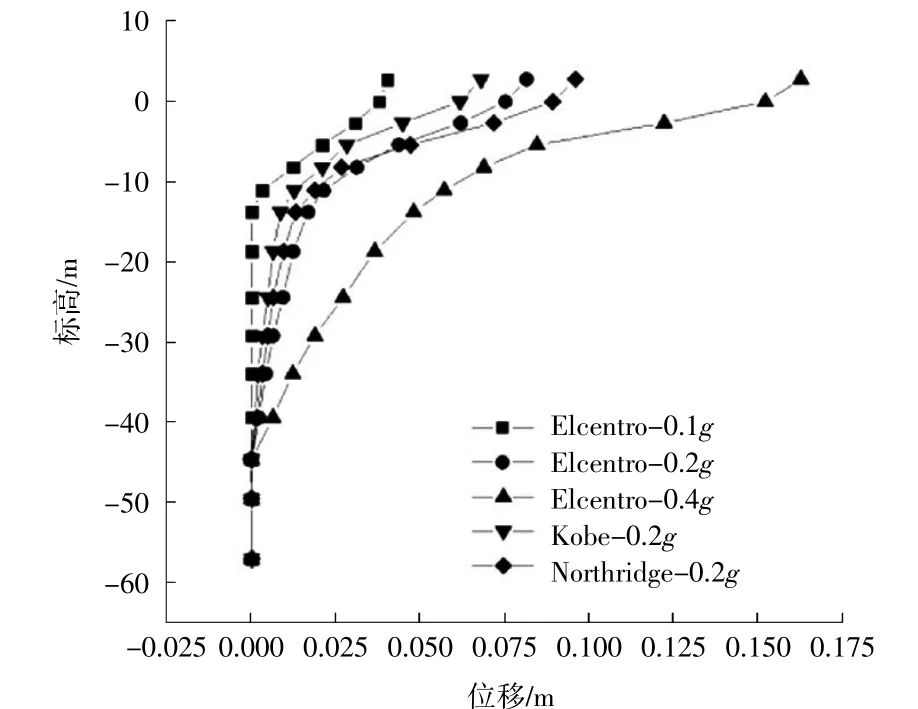
图7 不同强度地震波作用下1-1桩沿桩身的相对位移峰值Fig.7 Peak value of relativedisplacement of pile1-1 under seismic waves with different strength
桩身各点相对桩底的水平位移峰值从桩底到桩顶逐渐增大,并在桩顶处达到峰值,这表明桩顶处易发生破坏,需在设计时加强桩顶与箱板的连接强度。同时,由于上部结构预应力筋的存在,明显减缓了桩顶部位的位移增加趋势,有效减少了桩顶位移,并且其强度与位移峰值保持较好的线性增长,说明桩顶未发生较大破坏。另一方面,当地震波强度增大时,由于桩基离开泥面后土体的嵌固作用消失,桩基缺少土体约束,桩身相对位移从泥面到桩顶处的斜率发生了较大变化,桩基向海侧位移明显增大。
在泥面以下,本应与结构响应最强烈的Northridge波作用下的桩身位移峰值略小于EIcentro波的作用,而当观察点离开土体后,由于桩基与Northridge波的共振响应逐渐增强,桩身位移峰值快速增长。这表明频谱特性与结构自振频率接近的地震波对桩基位移的影响较大。
3.2 桩身弯矩及剪力响应
1-1~1-4号桩身在不同地震波强度下的弯矩及剪力响应峰值如表2所示。

表2 不同强度EIcentro波作用下桩顶弯矩及剪力响应峰值Table 2 Peak value of moment and shear response of pile-head under EIcentro waves with different strength
在同一地震烈度下,单独对比表中1-1、1-2及1-3、1-4两组桩基可知,随着桩基入土长度的增大,桩顶弯矩和剪力峰值逐渐增大;而对比桩基1-2和1-3,桩顶弯矩和剪力随着入土深度的增大反而有所降低,这是因为在同一个排架下3、4号桩基数量较1、2号桩基增加了1倍,每根桩仅承担一半的载荷,故单根桩的桩顶弯矩和剪力反而较1、2号桩有所降低。由于桩身在不同强度EIcentro波作用下弯矩响应峰值曲线类似,以强度为0.2g的EIcentro波为参考,如图8所示,除桩顶外,桩身还出现了两处弯矩峰值,分别在土层交界面以及泥面附近,这表明桩身易在土层改变处和泥面处产生较大弯矩,在抗震设计中需要重点关注。

图8 0.2g的EIcentro波作用下桩身弯矩响应峰值Fig.8 Peak of moment response of pileunder 0.2g EIcentro wave
4 系统能量耗散规律
结构在地震产生能量的输入与输出中存在着不同的能量转化与耗散,主要包括结构动能,阻尼耗散,黏性耗散以及损伤耗能等。以加速度峰值为0.2g的EIcentro波为参考,各能量变化时程曲线如图9所示。

图9 能量时程曲线Fig.9 Energy time-history curves
由图9(a)可知,系统能量耗散主要是阻尼耗散和黏性耗散,且能量耗散随着地震输入能量的增加而增加,结构动能在地震波施加前期波动较为频繁,后期趋于稳定;由图9(b)可知,损伤耗能随着时间的递增,在0.00~1.00 s、1.50~2.00 s和4.50~6.00 s期间发生了损伤耗能的骤然跳跃,表明结构此时发生了较大的裂缝破坏,瞬间释放了大量能量,属于脆性断裂耗能。这之间的耗能曲线呈阶梯状逐级上升,能量耗散为黏性耗散。
5 结语
本文采用ABAQUS软件对整体箱板式高桩码头进行地震响应分析,考虑了桩土相互作用、材料的非线性特征等,分析了结构面板、桩基在不同强度地震波作用下的加速度、位移、弯矩响应及系统能量耗散规律,判明了结构的脆弱环节,主要结论如下:
1)地震波频谱特性对结构的地震响应有很大影响,Northridge波的频谱与结构本身自振频率接近,结构产生共振,相比于其他两种地震波响应更加剧烈。
2)地震波作用下桩基在土层交界面和泥面附近产生弯矩突变,并且位移在桩顶处达到最大,表明这些部位容易发生破坏,在设计中应重点考虑其抗震性能,加强结构连接强度。
3)结构所布置的纵向预应力筋作用明显,能有效分担桩顶应力,使泥面以上桩身应力减小并在桩顶处趋于一致。另外,桩基数量对桩顶的弯矩和剪力也有较大影响,桩基数量增加,使每根桩承受的载荷减少,弯矩和剪力也随之减少。
4)阻尼耗散了大部分地震输入的能量,且随着输入能量的增加而增加。通过损伤耗能可以确定结构发生脆性断裂破坏的时间节点。
