FWD荷载下沥青路面弯沉盆几何特性分析

2020-11-25宋金华辛鹏飞

重庆交通大学学报(自然科学版) 2020年11期

宋金华，辛鹏飞

(河北工业大学土木与交通学院，天津 300401)

0 引言

据统计，2017年末全国公路总里程已达到477.35×104km，公路密度为49.72 km/102km2。其中：高速公路里程为13.65×104km，公路养护里程为467.46×104km，占公路总里程的97.9%[1]。由此可看出：我国公路养护、维修、改扩建等已成为公路工作者的主战场。基于此，对道路结构强度进行客观、准确的评估具有重要意义。

落锤式弯沉仪(falling weight deflector, FWD)具有无损检测且速度快精度高等特点，能很好地模拟行车荷载对路面的动态作用效果[2-3]。其检测结果为弯沉盆数据，蕴含了大量能反应路面强度的信息[4]。弯沉盆兴起于20世纪70年代初，之后才逐渐引入我国，我国对FWD研究起步相对较晚[5]。现有弯沉盆几何参数部分指标尚存有某些不足[6]。为更加准确、全面的表达路面结构强度，弯沉盆几何参数尚待进一步研究。

基于此，笔者针对我国半刚性基层沥青路面，在充分考虑动态荷载作用效果下，借助Abaqus软件构建三维有限元模型，对半刚性基层沥青路面进行动力有限元模拟，进而分析了其弯沉盆几何特性以及各结构层强度变化对弯沉盆曲线影响规律。

1 动力有限元分析模型

1.1 材料参数

根据我国沥青路面常用结构及文献[7]规定，此次分析将沥青路面简化为沥青混合料面层(AC)、半刚性基层(BC)、路基(SG)的3层结构，各结构层均为连续、均匀、各向同性的线弹性体。为便于分析各结构层模量和厚度变化对弯沉盆几何参数影响，笔者设定了一个基准路面结构，其结构参数见表1。

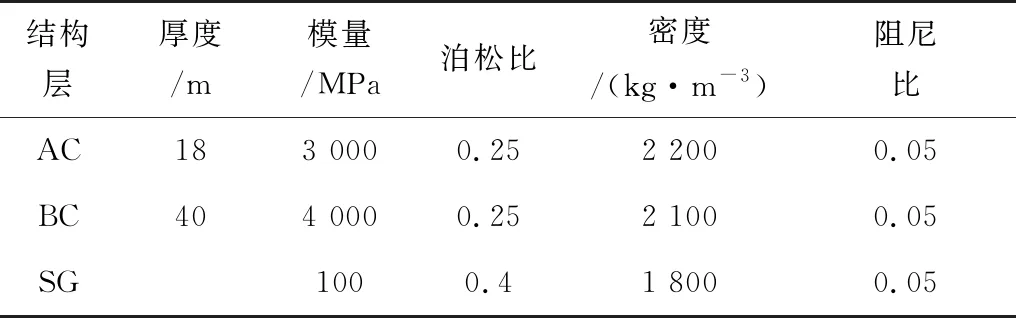
表1 基准路面结构参数

1.2 边界条件及网格划分

为避免模型边界反射动载波影响，当模型尺寸水平大于5 m且纵向深度大于11 m时即可满足计算要求[8]。单元类型采用C3D8R；网格划分采用全局尺寸0.05 m，测点沿行车方向2 m及垂直于行车方向0.15 m进行单精度局部细化处理；面层和基层尺寸为0.025 m，土基采用单精度局部细化；边界条件为行车方向与垂直行车方向分别进行XSYMM、YSYMM约束，模型底部为完全固定约束。

1.3 测点位置与载荷取值

测点布设位置和个数选取对路面强度准确性有很大关系[9]，该模型测点布设方案如表2。

表2 测点位置

将动态载荷简化为峰值为0.7 MPa[10]，持续时间为0.03 s的半周期正弦曲线荷载[11]；作用半径为0.15 m。

2 弯沉盆几何参数

随着对弯沉盆渐渐地深入了解，国内外大部分学者认为，单纯以最大弯沉值评价路面质量越发的理由不充分，且沥青路面设计新规范也做出了大幅度修改，改变了旧规范以设计弯沉值为设计指标的设计方法[7]。弯沉盆包含大量与路面结构强度相关的信息，其几何参数为评估路面强度起到不可或缺的补充作用。学界提出了弯沉盆几何参数指标，从不同角度反映弯沉盆形状，进而反应路面强度，其指标如式(1)～(5)。

A1=6[1+2(d1/d0+d2/d0)+d3/d0]

(1)

F1=(d0-d2)/d1；F2=(d1-d3)/d2

(2)

SCI=di-di+1, (i=0～7)

(3)

Qr=d7/d0

(4)

Qd=d0-d7

(5)

式中：A1为面积指标；F1和F2分别为形状系数；SCI为表面曲率指标；Qr为弯沉比；Qd为弯沉差；d0、d1、d2、d3、d7分别为C1、C2、C3、C4、C8各测点处弯沉值。

3 几何参数特性分析

3.1 面积指标

面积指标反映了路面结构整体强度，弯沉盆面积指标越大，则路面结构强度越低。目前面积指标除上列所式之外，还有另种面积指标算法，如式(6)：

A2=(5d0-2d2-2d4-d5)/2

(6)

面积指标与路面整体强度有关，则势必会随着某一结构层厚度或模量变化而发生相应变化，如图1。

对于面积指标A1而言，面层模量越大，面积指标应越小，而图1(a)变化趋势线斜率大于0，面层模量变化对面积指标影响规律表现为随着结构层强度增大，面积指标增大；对于面积指标A2，在土基模量变化过程中，面积指标随模量增加存在先增高后降低趋势，其变化规律表现为非单调性，如图1(b)。

对于面积指标而言，笔者认为应采用梯形公式计算d0～d8内的面积来作为衡量路面结构整体强度标准。有研究表明[6,12]：当土基模量固定时，弯沉盆曲线于C9后趋于一致；且发现弯沉曲线C1～C4范围内弯沉变化较剧烈，C4～C9弯沉值基本呈线性单调均匀变化，d4～d7基本分布于d3与d8的连线上，故面积指标如式(7)。

A3=50(2d0+3d1+2.5d2+15d3-22.5d8)

(7)

以各结构层厚度或模量变化为横坐标，面积指标值为纵坐标，绘制面积指标A3随模量或厚度等某单一路面结构层参数变化的关系曲线，如图2、 3。

由图2、3可知：面积指标无论是受模量还是厚度影响，其曲线图趋势线斜率均小于0，即变化趋势一致。故对于A1、A2而言，则能更好表达面积指标随各结构层模量、厚度增加而降低的变化规律。

3.2 d0/d1与E1/E2关系

一般而言：d0/d1(d0为荷载作用中心点处弯沉值，d1为距加载中心20 cm处弯沉值)仅与面层模量值大小有关，与面层与基层模量比E1/E2无关。在基准路面结构基础上，根据模量比值大小来控制基层模量变化。面层模量分别选取为2 000、4 000、6 000、8 000、10 000 MPa；模量比分别取0.25、0.50、1.00、1.50、2.00、2.50。d0/d1与模量比E1/E2关系曲线如图4。

从图4中可看出：模量比在0.5～2.5范围内，d0/d1随模量比增加其值稍有降低，变化不明显；d0/d1随面层模量增加其值呈层次式明显下降，且下降间隔逐级递减，这说明d0/d1仅与面层模量大小存在很大相关性。当模量比在0.25～0.50范围内，d0/d1不仅与面层模量有关，还受模量比影响，该区间内d0/d1变化幅度，远大于0.5～2.5整个范围内d0/d1变化幅度，d0/d1随模量比增加具有明显的降低趋势。故面层基层模量比值为0.5时是一个分界点，当模量比大于0.5时，可通过d0/d1与面层模量建立关系公式，大致预估面层模量。

3.3 曲率半径

弯沉盆曲线并非单纯的凹曲线，在0～20 cm之间为凸曲线，因此完整的弯沉盆曲线应该是类似于头小尾大的“S”型曲线，故拟合曲线方程采用三次多项式[12]，如式(8)：

y=a1x3+a2x2+a3x+a4

(8)

在此基础上，笔者对曲率半径进行进一步的分析。曲率半径是用来描述曲线在某一点处的弯曲变化程度。其三次多项式在任意点的曲率半径求解如式(9)：

(9)

采用三次多项式对某一路面结构组合下的各测点最大值进行曲线拟合，然后根据求解曲率半径公式，利用MATLAB求解出拟合公式在某一点的曲率半径。经过反复试算，分析表明在距载荷中心距离0.15 m处，即落锤与路面接触边缘，曲率半径与面层和基层结构层模量关系十分密切。图5中，0.15 m处曲率半径随面层或基层模量增加呈线性增长变化，线性拟合优度较好，尤其是面层，其可决系数为0.999 9，无限接近于1；并且从图5中可看出曲率半径对面层敏感性要优于基层。

4 结构层参数对动力响应影响

4.1 结构层模量与弯沉盆关系

结构层(面层、基层、土基)模量与弯沉盆关系曲线如图6。不同结构层模量下荷载中心处路表最大弯沉值如表3。

表3 不同结构层模量下荷载中心处路表最大弯沉值

4.1.1 面层模量与弯沉盆关系

沥青路面面层直接与车辆载荷接触，承受着竖直方向压力和水平方向上冲击力，并且在使用期内长期经受降水和气温等气候变化影响。故同其他层次相比，面层应具有足够高的结构强度，较好的水稳定性和温度稳定性，以满足道路交通正常运营。

为研究沥青路面面层模量对弯沉盆曲线影响，在基准路面结构的前提下，控制除面层外的结构层模量和厚度等参数不变，只改变面层模量情况下进行动态分析，结果如图6(a)。加载中心处弯沉值随模量增加逐渐减小，且C1～C2范围内各模量下弯沉曲线变化率表现为明显的非均匀性。

由表3可知，面层模量在2 000～7 000 MPa之间且增长率为1 000 MPa的变化过程中，荷载中心处两相临面层模量变化间弯沉值之差依次为：

1)0.025 638 mm(2 000～3 000 MPa)；

2)0.014 706 mm(3 000～4 000 MPa)；

3)0.009 710 mm(4 000～5 000 MPa)；

4)0.006 937 mm(5 000～6 000 MPa)；

5)0.005 254 mm(6 000～7 000 MPa)。

按照此规律变化，当面层模量达到某一足够大值时，若再想提升路面结构强度，仅提升面层模量是不合时宜的。故适当增加面层模量，可很好地提升路面结构整体强度，但当面层模量已足够大时，就需要考虑通过改变其它结构参数来综合考量路面结构强度。

4.1.2 基层模量与弯沉盆关系

基层结构是道路结构的重要组成部分，承受了来自面层车辆荷载并起到了很大的荷载扩散作用，是道路结构主要承重层，基层模量对弯沉盆影响如图6(b)。很显然，C1～C2范围内弯沉值变化与图6(a)不同，在基层各模量值下该范围弯沉盆曲线变化几乎都为平行；这又可得出另一个结论，即C1～C2范围内，弯沉盆曲线变化率受面层模量影响要大于基层模量影响。

整体而言，基层模量在2 000～8 000 MPa且增长率为1 000 MPa的变化过程中(表3)，荷载中心处两相临基层模量间的弯沉值之差依次为：

1)0.020 913 mm(2 000～3 000 MPa)；

2)0.012 922 mm(3 000～4 000 MPa)；

3)0.009 126 mm(4 000～5 000 MPa)；

4)0.006 926 mm(5 000～6 000 MPa)；

5)0.005 514 mm(6 000～7 000 MPa)；

6)0.004 548 mm(7 000～8 000 MPa)。

其变化规律与面层类似，同样在合理模量范围内可利用增大基层模量来提高路面整体结构强度，甚至可降低面层造价。

4.1.3 土基模量与弯沉盆关系

土基模量对弯沉盆曲线影响如图6(c)。从图6(c)中可看出：土基模量对弯沉盆曲线影响几乎是整体性的。由图6(a)、(b)表明：随着距荷载中心距离越来越远，面层和基层模量影响变化范围急剧缩减，1.8 m处测点弯沉几乎重合；而图6(c)中土基模量改变对1.8 m处测点弯沉影响较面层和基层模量来说要大得多。

当面层模量从2 000 MPa增加到7 000 MPa时，荷载中心处弯沉值从0.190 011 mm降到了0.127 766 mm，减小了约32.76%；基层模量从2 000 MPa增加到7 000 MPa时，其弯沉值从0.198 208 mm降到了0.142 807 mm，减小了约27.95%；土基模量从50 MPa增加到300 MPa时，其弯沉值从0.194 941 mm降到了0.115 912 mm，减小了约40.54%；土基模量对弯沉值影响变化率远超面层和基层。这表明土基结构强度对道路结构整体强度影响非常大，土基强度处理不容忽视，良好的土基条件是道路结构长期稳定正常使用的重要保证。

4.2 结构层厚度与弯沉盆曲线关系(图7)

由图7(a)可知：面层厚度越厚，路表最大弯沉越小，且变化幅度越来越小。即面层厚度在合理变化范围内对提高路面结构强度有一定作用。基层厚度对弯沉盆曲线影响如图7(b)，该影响与面层厚度变化趋势类似，C1～C2范围内各弯沉盆曲线近似平行变化。但通过比较两者对C1处弯沉值影响效果，可看出基层厚度对C1处弯沉值影响范围要大于面层厚度。

面层厚度对弯沉曲线影响规律与其模量影响规律大致相似，但又有略微不同，C1～C2范围内不同结构层厚度的弯沉盆曲线变化几乎都为平行。纵观图7～11，唯有面层模量变化时，C1～C2内最大弯沉曲线是非平行变化的，更进一步说明面层模量与距荷载中心20 cm范围内弯沉变化关系十分密切。

表4为不同结构层厚度下荷载中心处路表最大完成值。由表4可知：当面层厚度从10 cm增加到30 cm时，荷载中心处弯沉从0.184 704 mm降到了0.141 439 mm，减小了约23.42%，与改变面层模量相比，该弯沉变化明显小于32.76%。故增加面层厚度不仅效果不如增加面层模量，且面层厚度提升后的造价必然大幅度上涨。基层厚度从30 cm增加到60 cm过程中，弯沉从0.197 691 mm降到了0.125 803 mm，减小了约36.36%，与改变基层模量相比，该弯沉变化明显大于27.95%。基层模量和厚度均较小时，对于提高路面强度、增加厚度方式要优于增加模量。

表4 不同结构层厚度下荷载中心处路表最大弯沉值

5 工程实测检验

为对所建模型及上文所修正的几何参数进行实测验证，笔者选取两条道路进行对比分析。第1条路是以LC高速公路为依托，第2条路以QH城市主干路为依托，借助于落锤式弯沉仪对这两条半刚性基层沥青路面进行路面弯沉测试。从两条路中各选取其中一个测试点来进行比较，实测弯沉盆数据与有限元模拟计算数据对比结果如表5。

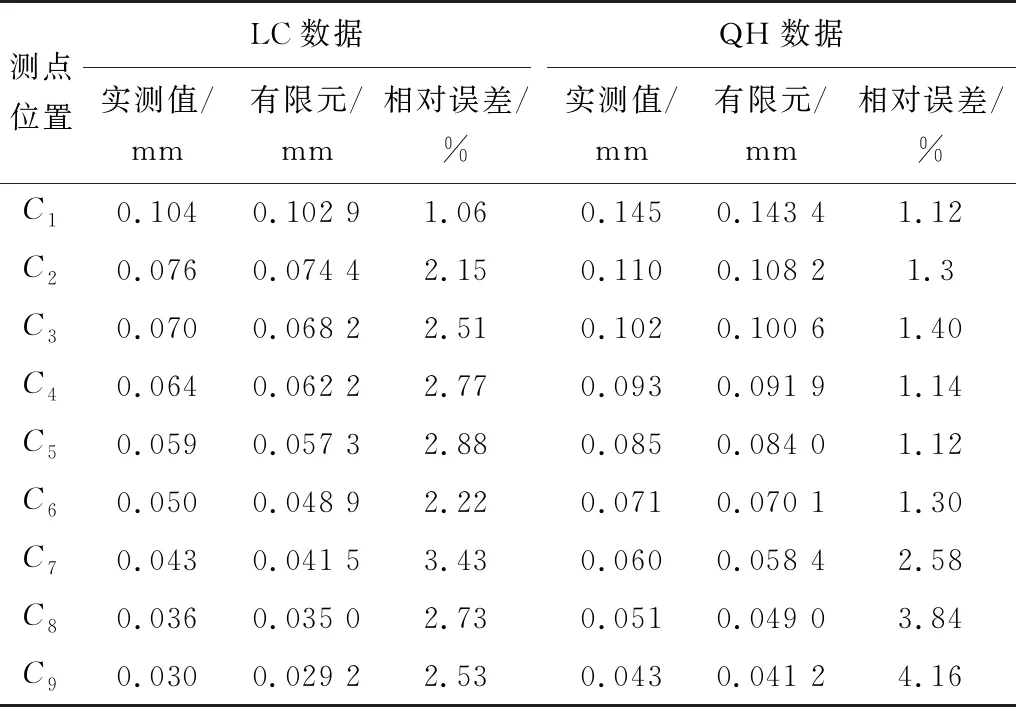
表5 LC和QH实测数据与有限元结果

从表5可看出：LC高速公路实测值与有限元计算值最大相对误差为3.43%；QH城市主干路实测值与有限元计算值最大相对误差为4.16%，两者误差均在允许范围内。整体而言，LC、QH两路的有限元计算与实测弯沉值相差不大，模拟计算与实测弯沉盆变化规律也非常吻合，因此，动力有限元方法能较为真实地模拟落锤式弯沉仪对路面动力响应。

根据实测弯沉盆计算面积指标A3。其中：LC路段A3=44.8，QH路段A3=65.1。通过对比表5中两路段实测弯沉盆值，并结合两路段面积指标A3可看出：弯沉盆值越大，对应A3值越大，即面积指标A3能很好反应路面结构强度，进而也说明了面积指标A3评价路面结构强度的可靠性。