有轨电车防撞的共轭梯度检测方法
2020-11-25刘亚辉闫晓茹
王 华,刘亚辉,闫晓茹
(四川交通职业技术学院 ,四川 成都 611130)
0 引 言
智能交通系统(ITS)在今天已为中国交通运输行业所熟悉,既被作为交通运输领域前沿科技的代表之一,又被作为交通现代化的标志[1]。如何有效地将数据通信技术、计算机信息处理技术应用于交通运输管理体系是当务之急。有轨电车防撞系统作为ITS的一项关键技术[2],是整个交通运输管理系统的重要组成部分。
然而,当前有轨电车的交通运行安全主要由车辆运行司机及交通信号系统保障。它没有独立路权,与社会车辆存在交叉路段,并且行驶过程中受光线、建筑物、路面积水、树木、路标、坡道、弯道等的影响。因此,如何避免有轨电车与社会车辆、行人碰撞而发生的交通事故,确保有轨电车的行车安全,探测电车前方障碍物并根据障碍物的危险程度提示司机采取有效驾驶措施是非常必要的。目前,有轨电车采用的障碍物探测系统有多种[3],如激光雷达系统、毫米波雷达系统等,它们均需要对雷达的回波信号进行滤波处理。
针对采用均匀线性阵列(ULA, uniform linear array)[4]的有轨电车雷达防撞系统,进行空时自适应处理(STAP, space-time adaptive processing)[5]。在STAP中需要求解大型维纳霍夫方程,直接方法解决这个问题要求矩阵求逆,运算量为R(J3N3),其中J为通道数,N为脉冲数。通常情况下,空时协方差矩阵的维数较大,直接求逆法运算量很大,因此,迭代算法越来越受到重视。在STAP中,采用迭代法不仅可以经过很少迭代求得精确权向量,还可以得到系列Krylov子空间STAP方法。在众多的迭代方法中,共轭梯度法(CG, conjugate gradient)[9]在Krylov子空间中寻找权向量的解,运算量为R(J2N2)。JIANG Chaoshu等[6]已经证明,它在迭代过程中产生了一系列检测器,且该检测器具有CFAR特性,其虚警概率与迭代次数无关,即与理想匹配滤波器(MF, matched filter)相同。笔者将共轭梯度算法应用于有轨电车的雷达防撞系统,获得一系列具有CFAR特性的最优检测器。
1 信号模型
有轨电车雷达防撞系统模型可以简化为图1,重点关注匹配滤波器部分。
针对采用ULA的有轨电车雷达防撞系统,假设待检测信号为J通道信号s(n)∈CJ×1,它会受到空时干扰c(n)的影响,则[1]:
H0:x(n)=c(n)
(1)
H1:x(n)=as(n)+c(n)
(2)
式中:x(n),n=1,2,…,N为第n个接收向量;a为s(n)的确定的但未知的复幅度。令s=[sT(1),sT(2),…,sT(N)]T,c=[cT(1),cT(2),…,cT(N)]T,x=[xT(1),xT(2),…,xT(N)]T,则它们均为JN×1维的复向量。在STAP中,空时导向向量s是已知的。对ULA雷达,s可表示为:
s=st⊗ss
(3)
(4)
2 共轭梯度法检测原理
通过将CG算法应用于滤波器权向量的求解,可以获得一系列近似权向量,对应一系列最优检测器,且该检测器具有CFAR特性,其虚警概率与求解最优权向量的迭代次数无关,也就是说,这些检测器均是MF。
2.1 MF和AMF检测器
为了获得共轭梯度法检测器,先推导MF和AMF检测器[7]。针对文中的信号模型,在H0假设下,条件概率密度函数为:
(5)

(6)
由式(5)和式(6)可知,似然函数为:
(7)
对式(7)求对数得:
lnΛ=a*sHR-1x+axHR-1s-aa*sHR-1s=2Re{a*sHR-1x}-|a|2sHR-1s
(8)
根据最大似然估计的概念可得:
(9)
令
(10)
得:
(11)
将式(11)代入式(9)中,可得MF的检测统计量为:
(12)
其中η是MF的检测门限。MF的权向量与R-1s呈线性关系:
wMF=αR-1s
(13)
式中:α为任一实数。
当根据辅助数据估计得到空时协方差矩阵时,此时的检测器称为AMF。因此,AMF的检测统计量可表述为:
(14)
2.2 共轭梯度法检测器
CG算法是求解线性方程组的一种迭代方法[8-10],该法在迭代过程中可以产生一系列快速收敛的近似解{w(k)}。
对于Rw=s这种对称正定矩阵问题,CG算法主要考虑如何极小化下列函数:
(15)
式中:w∈n,R∈n×n,并且R对称正定。
算法1(CG算法):如果R∈n×n对称正定,s∈n,w0∈n为初始近似值(Rw0≈s),则根据下列算法,可以计算出w∈n,使得Rw=s
k=0
r0=s-Rw0
whilerk≠0
k=k+1
ifk=1
p1=r0
else
pk=rk-1+βkpk-1
end
wk=wk-1+αkpk
rk=rk-1-αkRpk
end
w=wk
在实际应用[8],由于协方差矩阵R的维数多,直接矩阵求逆的运算量大,采用CG算法,少于JN次迭代就可以获得权向量,并且产生一系列近似权向量wk(k=0,1,2,…)。
在(14)式中,每一个权向量wk都可以形成一个检测器:
(16)
因此,式(16)实际上是一系列检测器,称为CG-AMF检测器。
定理1:如果R=I+B为n×n对称正定矩阵,且rank(B)=r,则算法1最多r+1步收敛。
算法1和直接矩阵求逆法的运算复杂性分析如下[10]:
采用直接法对协方差矩阵求逆,需要(JN)3次乘法,算法复杂度为R(JN)3。采用CG算法,一次迭代仅需1次矩阵、向量乘法,算法复杂度为R(JN)2;2次标量乘法,算法复杂度为R(1);6次向量、标量乘法,算法复杂度为R(JN)2。在实际应用中,协方差矩阵通常具有定理1的低秩校正结构,最多r+1步收敛,并且r通常远小于JN,因此,CG算法会快速收敛,运算复杂度较直接矩阵求逆法可大大降低。
2.3 共轭梯度法检测器特性
分析两种情况下CG-AMF检测器的性能。
JIANG Chaoshu等[6]已经证明,当空时协方差矩阵R是任意的,无论迭代多少次,CG-AMF都是恒虚警检测器。对于给定的虚警概率,检测概率由CG-AMF检测器的输出信干噪比决定,不随迭代次数变化而变化。在K维Krylov子空间中,CG-AMF检测器在第K次迭代时输出信干噪比最大,因此,它是最优检测器,并且满足定理2。
定理2:对第k个CG-AMF检测器,有如下3个性质:
wk是最小线性均方估计器,在所有k维Krylov子空间线性估计器中,它使wk最小,其中:
(17)
κ(R,s,k)≜span{s,Rs,R2s,…,Rk-1s}
(18)
在κ(R,s,k)的线性估计器中,wk相应的输出信干噪比最大:
(19)
如果x~CN(as,Rc),那么,在H0假设下,a=0,在H1假设下,a≠0。wk的虚警概率Pfa,k和检测概率Pd,k为:
Pfa,k=exp (-ηk)
(20)
(21)
式(20)说明,对任意k,CG-AMF检测器都是恒虚警检测器。由于κ(R,s,k)⊆κ(R,s,k+1),可以得出ρk≤ρk+1。因此,CG-AMF检测器是由降秩和全秩AMF检测器组成的系列CFAR检测器。当迭代次数增多时,检测概率提高,运算复杂程度也提高。对于给定的检测概率,可以通过选择合适的降秩CG-AMF检测器以降低计算代价,而不需完全迭代。
在有轨电车防撞雷达系统常见结构中,当R=Ri+σ2I+Δ时,扰动项Δ是决定性干扰。在没有干扰时,CG算法经过第r+1次迭代收敛,因此,如果r较小,它获得AMF权向量的运算量要比直接法求矩阵逆少很多。如果有扰动项Δ时,CG算法经过完全迭代才能收敛,那么CG算法在第r+1次迭代时的收敛情况需要考虑如下引理1和定理3:
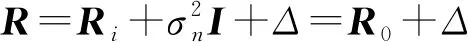
(22)
(23)
(24)
(25)
(26)
(27)
当扰动消失时可以得到:
(28)
式(28)说明,在一阶近似情况下,CG-AMF检测器wr+1收敛于AMF检测器wMF。
定理3:在满足引理1和一阶近似情况下,AMF和CG-AMF的输出信干噪比相同:
(29)
引理1指出,权向量之差wAMF-wr+1包含一阶扰动项,并且一阶扰动项在输出信干噪比中消失,可以忽略。定理3指出,一阶近似时,AMF和CG-AMF检测器的检测概率相同。当扰动很小时,即使采用CG算法,还是需要完全迭代,但是利用第r+1次迭代产生的中间结果wr+1,就可以获得与AMF检测器几乎相同的检测性能。
3 仿真数据验证
采用瑞利分布的杂波仿真数据进行验证分析。参数如下:
有轨电车运行速度vp=11 m/s;脉冲重复周期T=1/8 000 s;阵元间距d=0.04 m;杂噪比CNR=70 dB;虚警概率pf=0.01;通道数J=4;脉冲数N=32。
仿真数据验证结果如图2~图7。
在图2中可以看出,128(JN=4×32=128)维的协方差矩阵有128个特征值,并且有大约40个由杂波和干扰形成的特征值,其余为由高斯白噪声及少量扰动形成的特征值,这与上文分析相符。
图3、图4和图5中,权向量经过远少于128次的CG法迭代即收敛,输出SINR随迭代次数增加而快速增加,检测概率在40步迭代后趋近于1,这比矩阵直接求逆获得滤波器的权向量节省了不少运算量,有利于降低成本,与分析一致。
在虚警概率为0.01的情况下,通过3 000次蒙特卡洛仿真,分别进行15步、40步CG法迭代,对比MF和CG-MF的检测性能,检测曲线如图6和图7。
由图6和图7看出,随着迭代次数的增加,CG-MF的检测性能趋近于MF,与理论分析相符。
4 结 语
主要研究有轨电车运行过程中周围的杂波、干扰和噪声的特征,将共轭梯度法匹配滤波器应用于有轨电车的防撞雷达系统中。理论分析、仿真数据表明,在共轭梯度法迭代过程中,不仅获得了一系列CFAR最优检测器,并且提高了运算效率,有利于降低成本。
