IGM-FM串联模型在高铁路基沉降预测中的应用
2020-11-25张献州夏晨翕蒋英豪陈建营
张献州,夏晨翕,陈 霄,蒋英豪,陈建营
(1. 西南交通大学 地球科学与环境工程学院,四川 成都 611756;2. 高速铁路运营安全空间信息技术国家地方联合工程实验室,四川 成都 611756)
0 引 言
我国首条高速铁路——京津城际,开通运营距今已十年,在工程建设、装备制造、运营管理等方面建设者们积累了不少经验。为了保障高速铁路高平顺、高稳定运行,对于路基、桥涵、隧道等线下工程的工后沉降近乎苛刻,在设计建设中甚至有“工后零沉降”的理念。高速铁路路基变形严重制约列车行车速度,对沉降变形标准历经了认识-实践-再认识的过程。高速铁路路基沉降初期沉降速率快,沉降量大,后期趋于稳定,总体呈现“变形量级小、数据相对波动大”的特点,根据Q/CR 9230—2016《铁路工程沉降变形观测与评估技术规程》(下简称《规程》)将适用于路基段的评估指标总结于表1。此外,沉降过程管理中的监测时间、监测频次,设计总沉降量和最终沉降量等也是重要评估指标。

表1 无砟轨道路基沉降评估过程指标
路基沉降预测方法主要有3类:理论公式法、数值计算法和以实测数据为基础的曲线回归法。《规程》中推荐了包括双曲线法[2]、三点法、指数曲线法、Asaoka法等国内外比较成熟曲线回归法,及灰色系统、神经网络在内的系统理论法[3]。
因基准点和工作基点修正、施工破坏、测点转移、接管等情况造成的沉降监测点前后两期数据差异变化的情况称为断高。这种异常处理不当会影响高速铁路路基工程沉降评估的判断和分析,当前修正断高普遍采用“归零法”,即假设在断高时无沉降量产生,将当期观测成果归零处理。叶茂[4]提出卡尔曼滤波迭代法,分别使用高程数据和高差数据来修复断高,以此提高了预测精度。高速铁路路基沉降监测数据属于时序数据,上述各情况产生的断高可视为确定监测时间序列下连续数据缺失。为避免沉降监测数据的浪费和重要监测信息的缺失,综合考虑沉降速率、施工工况和时间间隔等因素的影响,利用断高数据相邻期实测沉降量建立插值函数来补全断高当期数据。
1 改进GM(1,1)模型
灰色系统能够有效解决呈“小样本、贫信息”的不确定数据,传统GM(1,1)模型建模步骤如下:
1)将样本序列x0=(x0(1),x0(2),…,x0(n))一次累加生成,以弱化其随机性得到1—AGO序列如式(1):
x1=(x1(1),x1(2),…,x1(n))
(1)
2)由式(1)得白化微分方程如式(2):
(2)
式中:α为发展系数,μ为灰作用量。
3)GM(1,1)模型的灰微分方程如式(3):
x0(k)+α·z1(k)=μ
(3)
式中:背景值z(1)(k)为x(1)的均值序列如式(4):
(4)
4)将白化微分方程积分,利用最小二乘法求解参数α和μ,得到响应序列如式(5):
(5)
5)利用一次累减得到还原序列如式(6):
(6)
构建的GM(1,1)模型是否适用于中长期预测,视发展系数α的大小而定。当-α≤0.3时,GM(1,1)模型适用于中长期预测,当0.3≤-α≤0.5时,GM(1,1)模型适用于短期预测。
以上为传统GM(1,1)模型建模过程,其存在的不足为3个方面:
1)传统GM(1,1)模型适用于等时距观测序列,现场釆集的观测序列一般很难达到等时距要求;
2)传统GM(1,1)模型以x1(1)作为迭代初值有两个缺陷缺:①由最小二乘计算之后,拟合曲线并不都通过点(1,x1(1));②x1(1)是样本序列中第一个值,并不通过累加生成产生,规律性不强且与未来预测数据时间关联度最不密切;
3)传统GM(1,1)模型以紧邻的2个1-AGO数据均值作为背景值的构造虽然简单,但对剧烈变化的序列适应性差[5]。
针对上述缺点,笔者分别进行优化。
1.1 非等时距GM(1,1)模型构建
构建非等时距GM(1,1)模型的思想是以观测序列的时间间隔作为乘子。记观测序列时间间隔为Δki=ki-ki-1≠const(i=2,3,…,n),则:
(7)
最小二乘法进行求解待估参数如式(8):
[α,μ]T=(BTB)-1BTY
(8)
式中:
在初始条件x1(k1)=x0(k1)下,解得时间响应序列,一次累减后还原值如式(9):
(9)
1.2 基于背景值的优化
对区间[k-1,k]上的白化微分方程积分,如式(10):
(10)
式(10)与式(3)比较,误差来源主要是应为背景值z1(k)的构造不同造成。传统GM(1,1)构造的背景值z1(k)实则为图1中梯形abcd的面积,GM(1,1)模型拟合曲线所围成曲边梯形面积与梯形abcd面积值差值为ΔS。当样本序列变化平缓时,背景值z1(k)接近于实际面积,误差可忽略,认为构造的背景值合适。
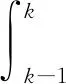
1)令:
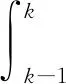
(11)
构造齐次指数函数如式(12):
x1(t)=ReAt
(12)
带入式(11)得式(13):
(13)
(14)
将式(14)带入式(13)得式(15):
(15)
式(15)即为基于齐次指数函数的背景值优化模型。
1.3 基于迭代初值的优化
在传统模型中调整或修改迭代初值优化。通过最小二乘原理优化初值和添加初值修正因子[9-10]。笔者充分利用已占用的“最少信息”,对原初始值x0(1)增加一个修正参数λ作为迭代初值,将其带入GM(1,1)的响应函数后经过还原,则非等时距GM(1,1)预测新模型如式(16)[11]:
(16)
(17)
求微分后得式(18):
(18)
式(18)计算可得式(19):
(19)
1.4 新陈代谢GM(1,1)模型
高速铁路路基沉降变形数据中,距预测期次越远的数据预测效果越差.建立新陈代谢GM(1,1)模型目的为:剔除不能体现系统当前特性的最老信息x0(1),置入最新信息x0(n+1),用新组成的一组数据序列进行预测[12]。
笔者将经过上述基于齐次指数函数的背景值优化和初值修正的非等时距GM(1,1)模型称为IGM(1,1)模型(improved grey model)。IGM(1,1)模型属于修正后的指数函数模型,可以较好地拟合高速铁路路基沉降监测数据的变化趋势。
1.5 精度检验
IGM(1,1)模型预测完成后需作精度检验,相对误差和后验差检验指标为[13]:
根据验差比值和小误差概率的值,与表2对比检验IGM(1,1)精度。

表2 模型精度等级
2 傅里叶变换修正IGM(1,1)模型
对IGM(1,1)模型的预测残差作傅里叶变换(FFT),可以有效剔除数据频谱的噪声(高频段)和保留本质信息(低频段),提高预测精度。
(20)
C=(FTF)-1FTe1
(21)
式中:
F=
3 马尔科夫二次残差模型
IGM(1,1)虽然克服了传统GM(1,1)建模的缺陷,能够利用少量样本数据进行高精度的预测,但该模型应用仍有存在对于随机波动性强的沉降监测数据,拟合—预测的中长期预测会有较大偏差的局限性。Markov模型能通过样本序列的波动范围预测出研究变量的预测范围[15]。应用Markov对一次残差进行修正,使其既能反映状态的随机过程,又能有效预测出路基未来一次的沉降范围。
设随机系统W在时刻t的状态为in,系统在t+1时刻的状态只与t时刻状态有关,即:
p{Wn+1=in+1|W0=i0,W1=i1,…,Wn=in}=p{Wn+1=in+1|Wn=in}
(22)
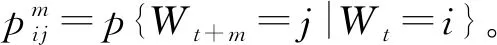
(23)
描述系统m步状态转移概率矩阵(transition probability matrix)为式(24):
(24)
PT(s)=PT(0)Ps(⊗)
(25)
因此,已知系统初始分布和转移概率矩阵,即可对下一期的系统分布进行预测:
M(k+1)=φ1υ1+φ2υ2+…+φnυn
(26)
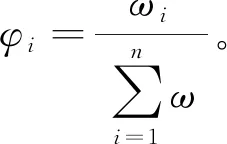
4 IGM(1,1)-FM组合预测模型
高速铁路路基沉降预测评估中,诸多单项模型应用条件苛刻,建模过程中只能考虑单一沉降因素,直接应用不能准确反映路基全生命周期内的沉降变形规律。如双曲线法仅适用于恒载以后的数据,预测结果偏保守;三点法的起始点选取满足等时距,且要求原始数据随时间变化收敛等条件[17]。高速铁路路基工程结构特性不同、地质情况复杂、总体变形量级小,通过单一模型的组合,分散单个预测模型特有的不确定性,取长补短,提高预测整体精度和稳健性,使之有效反映变化规律。
4.1 残差修正型串联式组合模型
模型组合方法从结构上可分为串联、并联、嵌入和混合式[18]。串联式组合预测模型认为,沉降变形数据符合变形趋势项、变形周期项和变形随机项叠加的规律[19],即
xt=Qt+Zt+St
(27)
式中:Qt为变形趋势项,代表数据的发展趋向,有一定的延续性和连贯性;Zt为变形周期项,代表数据的规律性波动;St为变形随机项,是因随机噪声引起的数据变动。
高速铁路路基沉降量级小,若数据分解不合理会终导致残差量级过小甚至小于测量误差,反映不出路基沉降规律。笔者研究高速铁路路基沉降变形数据的合理化分解,选取适当模型对数据进行预测,提取趋势项保留随机项,则周期变化存在于其残差序列中。建立一种残差修正型串联式组合模型在理论上具有可行性,模型流程如图2。
模型建立具体步骤如下:
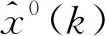
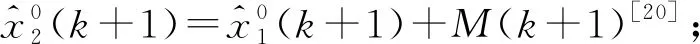
笔者将上述构造的组合预测模型定义为IGM(1,1)-FM残差模型。
4.2 模型效果评价
为了反映笔者建立的组合预测模型效果,笔者拟采用平均绝对百分比误差(mean absolute percentage error,MAPE)和《规程》中相关系数η来评价指标进行检验:
(28)
(29)
5 工程实例
某高速铁路路基DK0511+610断面沉降板0551610L采用天宝DiNi03电子水准仪按二等水准测量方法进行水准测量,实测数据共126 d,对应的荷载-时间-沉降(P-T-S)曲线如图3,其中负值表示下沉。
5.1 沉降数据补插
图3中,第8、14、21、70、82、84 d经过“接管”处理,传统的方法是将当天沉降量“归零”。拟合起点为第84 d(填筑完成日期),故当期沉降量至关重要,不能直接“归零”,笔者采用线性插值法实现数据补插。第8、14、21、70、82、84 d线性补插之后单次沉降量为0.63、0.60、0.57、0.35、0.30、0.269 mm,重新计算得累计沉降量如表3。
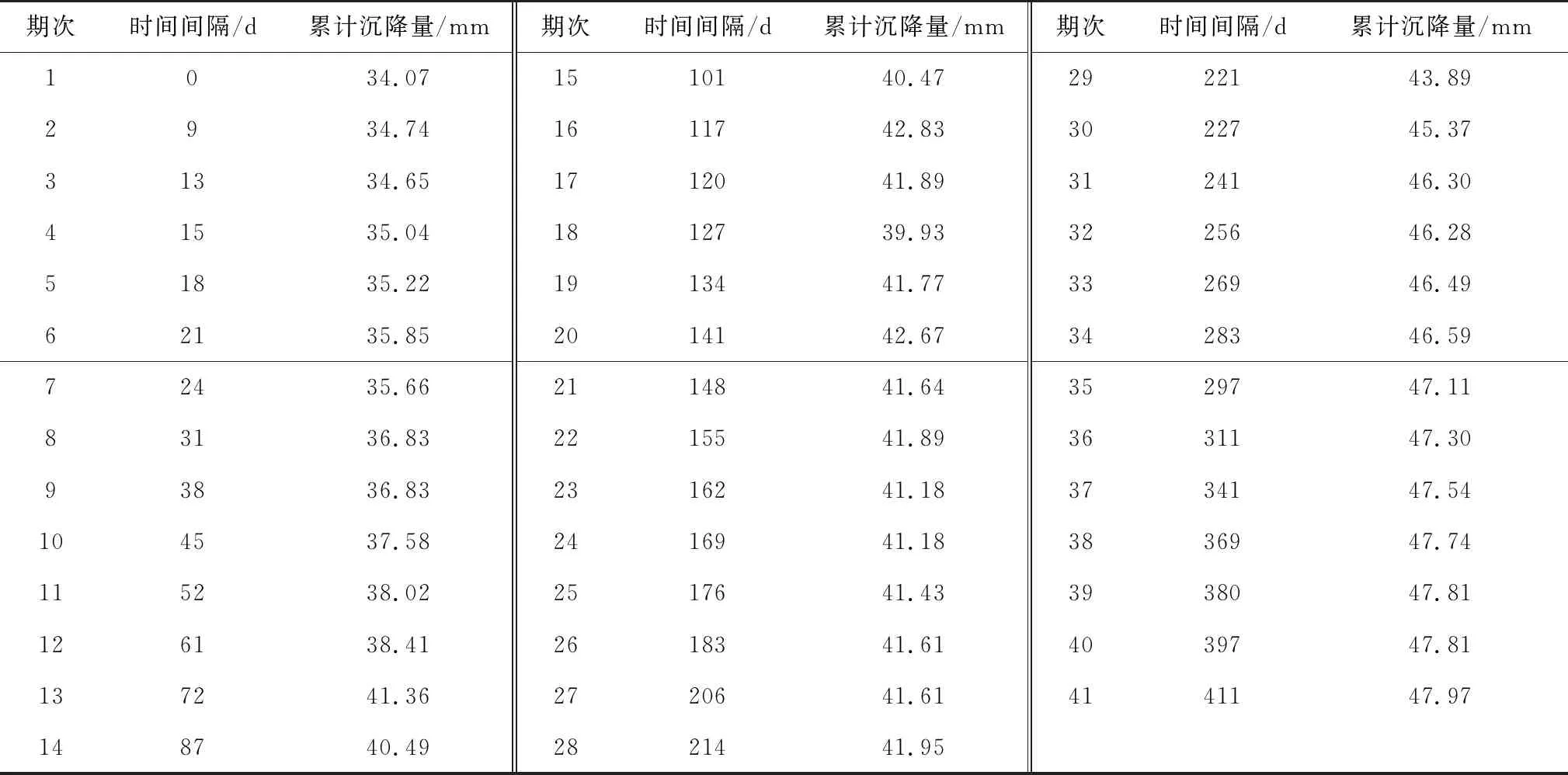
表3 某高铁路基0551610L1累计沉降量
5.2 IGM(1,1)-FM组合预测
进行两步预测,具体思路为:首先,选取前39天路基沉降观测数据x0={x0(1),x0(2),…,x0(39)}作拟合建模,使用IGM(1,1)-FM模型预测第40 d沉降量;接着将预测的第40 d沉降量置入模型中,剔除第1d数据,得到新的序列x0={x0(2),x0(3),…,x0(40)},对第41 d沉降量进行预测。依次剔除更新,最终完成第41 d预测。以下为预测第40 d沉降量过程:
IGM(1,1)模型验后差比值θ=0.346 9,小概率误差Ω=1.00,模型精度等级为一级;发展系数-α<0.3,适合于中长期预测。
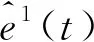
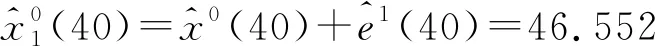
上述区间已包含整个残差范围,根据Markov原理首先对一步状态转移个数进行统计,如表4。
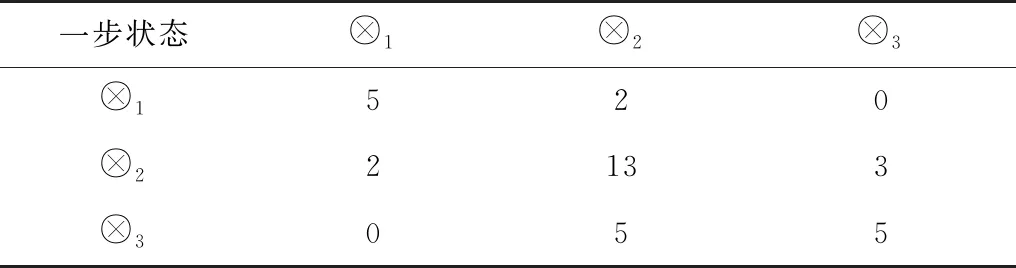
表4 一步状态转移个数统计

表5 状态转移表
5.3 预测效果评价
将第40 d的IGM(1,1)模型和IGM(1,1)-FM拟合值和预测值如表6按照3.2求得δMAPE和相关系数η,进行效果评价。
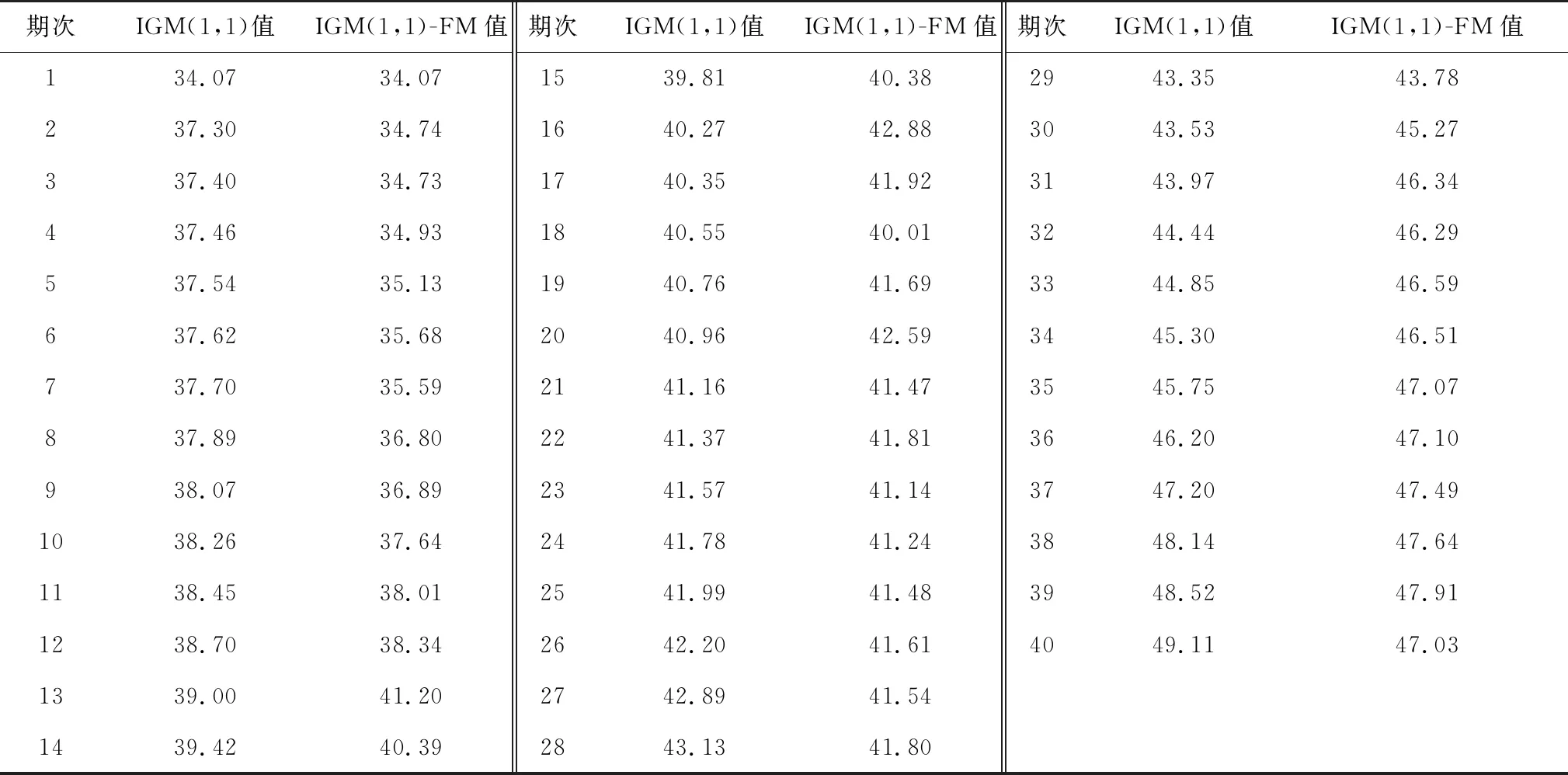
表6 模型拟合40 d预测值
将预测的最后两期模型精度列于表7。
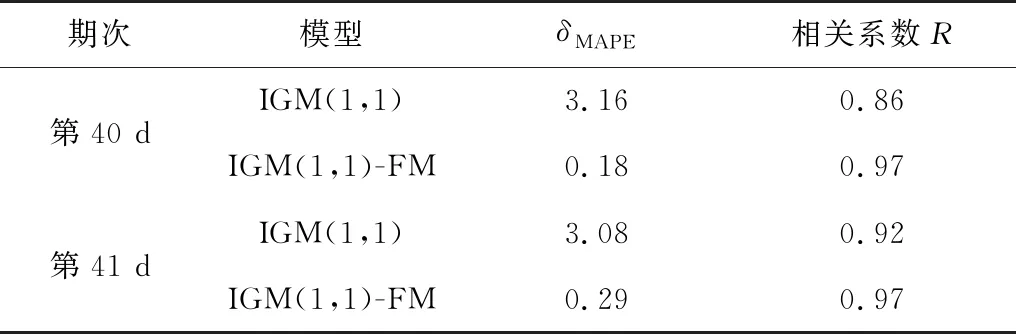
表7 模型精度对比
δMAPE值能反映预测值的精度,δMAPE<10为精度极佳。由此可分析,IGM(1,1)-FM模型优化精度得到进一步提高。相关系数R能反映预测趋势的一致性,根据《规范》“曲线回归相关系数不应低于0.92”[1]的要求,IGM(1,1)-FM模型的R值更高,说明预测和实测相关性满足规范要求,且一致性更高。
6 结 论
1)针对“断高”数据笔者考虑利用断高数据相邻期实测沉降量建立插值函数来补全断高当期数据,避免了沉降监测数据的浪费和重要监测信息的缺失。
2)GM(1,1)模型建模过程中尚存诸多缺陷,笔者构建了基于齐次指数函数的背景值优化和初值修正的非等时距IGM(1,1)模型(improved grey model),运用“剔就添新”的新陈代谢思想预测高速铁路路基沉降第40、41 d数据。
3)对于随机波动性强的高速铁路路基沉降监测数据,IGM(1,1)模型呈单一指数型变化,拟合—预测的中长期预测效果会有较大偏差。笔者基于高速铁路路基沉降变形数据的合理化分解,利用傅里叶级数和Markov状态转移矩阵对一次残差进行二次组合预测,更好地拟合高速铁路路基沉降监测数据的变化趋势。
