基于LSTM引入客车占比特征的短时交通流预测
2020-11-25翁小雄
翁小雄,郝 翊
(华南理工大学 土木与交通学院,广东 广州 510000)
0 引 言
准确、及时的交通流信息对于智能交通系统至关重要。近年来,交通数据呈爆炸式增长。在交通大数据背景下,短时交通流分析与预测工作不断深入。现有的交通流预测方法多采用传统时间序列模型[1],如李琦等[2]应用的移动平均法、J.RICE等[3]应用的KNN算法、M. S. AHMED[4]应用的ARIMA方法和近年来提出的组合模型法等。但以上算法均存在固有缺陷,导致对实际交通流预测效果不理想,这种情况促使笔者重新思考基于大数据的交通流预测问题。
最近,LSTM神经网络作为一种拥有较强“记忆”能力的深度学习方法,已成功应用于分类任务、自然语言处理[5]、降维、物体检测[6]、运动建模等场景中。国内外许多学者也将其应用于交通工程领域,例如:2015年,X.L.MA等[7]利用其长时间学习优势,将LSTM应用于交通流预测;WU Yuankai[8]等基于LSTM对交通流的时空相关性进行了研究;2018年,王祥雪等[9]搭建基于LSTM的城市快速路短时交通流预测模型等。但是以上预测模型的搭建均以交通流量为单一特征进行输入,并未挖掘交通流数据中隐含的周期性部分,忽略了其对交通流预测的影响。
笔者通过对历史交通流数据的分析,证明客车占比是交通流数据中隐含的周期性部分,提出了增加客车占比特征的LSTM模型,并以广州北环高速某收费站为例进行交通流预测的实例分析。结果表明:引入客车占比特征的LSTM预测模型降低了短时交通流预测的误差,提高了预测的正确率。
1 交通流数据分析
1.1 数据集介绍及数据处理
1.1.1 数据集介绍
笔者所采用数据为广东省广州市北环高速公路某收费站2015年12月14日—20日一周的车流数据,共183 033条数据记录。每条数据记录中包含路网编号、路段编码、站编号、车道编号、车道类型、日期及时间、车型、车种、车牌号码、客货标识等信息。其字段和数据类型如表1。
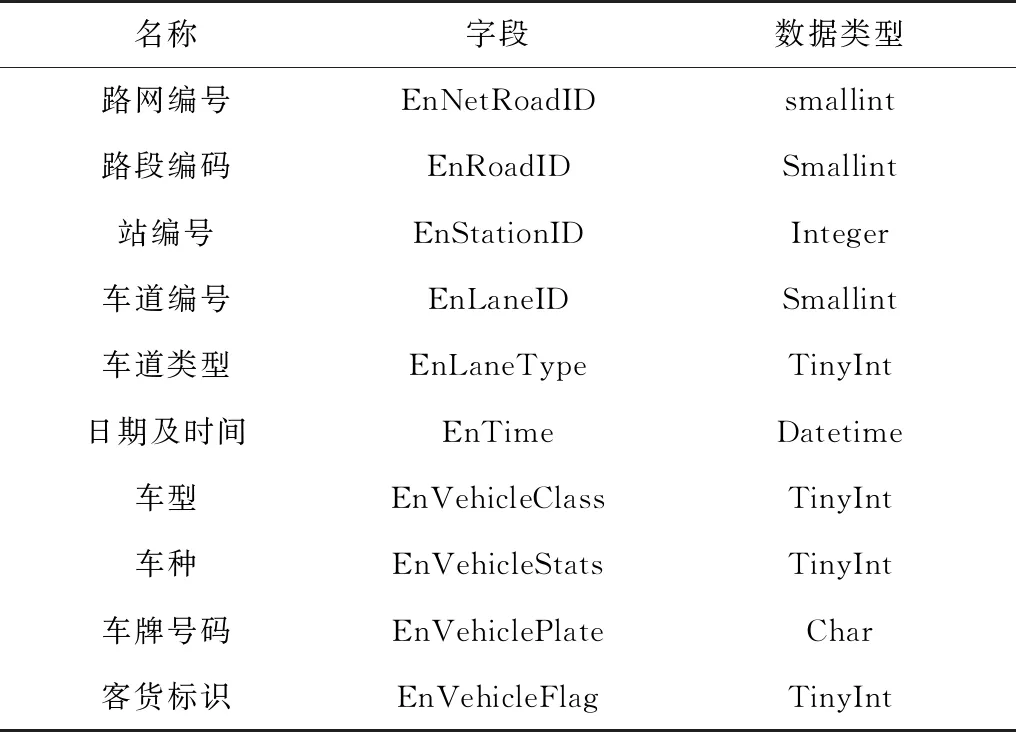
表1 数据集说明
抽取站编号、日期及时间、车型及客货标识4个关键数据进行分析:站编号代表具体收费站,数据类型为整型;日期及时间数据为Datetime型;车型数据为整型,1,2,3,4,5分别为交通部统一标准的一类车至五类车的车型;客货标识数据为整型,1表示客车,2表示货车。数据实例如表2。

表2 数据实例
1.1.2 数据集处理
去除数据异常值、空值并进行线性归一化,最终获得9号收费站共182 539条车流信息数据。对数据按时间顺序进行排列,设定统计时间间隔为15 min,得到672个时间序列,一周交通流量数据如图1。
同时,计算此收费站每个时间序列的客车占比。设第i个时间序列内车流量总数为Mi,客车车流数为Vi,则第i个时间序列内客车占比Ki的计算公式如式(1):
(1)
利用式(1)计算一周的车流数据中每个时序的客车占比情况,作出折线图,结果如图2。
从图1和图2看出,高速公路交通流量数据与高速公路客车占比数据呈现明显的周期性特征,与城市交通流理论中指出的大部分交通流量数据存在周期性相符合。这种特性不仅存在于周与周之间,不同的工作日之间,甚至一天内某些时段的交通流量数据也存在着相似。提取出交通流数据中隐藏的周期性部分可以帮助更好地理解交通系统,便于取得更准确的预测结果。
1.2 基于快速傅里叶变换(FFT)的周期性验证
1.2.1 FFT算法介绍
周期性模式可以理解为对于包含N个事件的时序数据库{E1,E2,E3,E4,…,EN},其中的事件总以固定时间间隔重复发生,则认为时间序列数据库具有该模式。周期性验证在信号处理领域是一个众所周知的问题。傅里叶变换是一种基础的信号处理工具,可确定数据中的频率分量。快速傅里叶变换FFT(fast Fourier transformation)是离散傅里叶变换(DFT)的快速算法[10],其根据离散傅里叶变换的奇、偶、虚、实等特性,对离散傅里叶变换进行改进,使计算机计算离散傅里叶变换所需要的乘法次数大为减少。利用FFT算法,将数据从时域转换至频域,通过频率函数可有效验证数据的周期性[11]。其计算公式如式(2)、式(3):
(2)
(3)
1.2.2 高速公路数据的周期性验证
利用1.2.1节介绍的快速傅里叶(FFT)算法对高速公路流量数据(图1)及客车占比数据(图2)进行周期性验证,分别绘制其功率频谱图,结果如图3、图4。
从图3和图4中可看出,高速公路流量数据及客车占比数据均有明显周期性,且两者的最小周期相等,均为96。由于统计时间间隔为15 min,则96个时间序列刚好构成一天(24 h),亦即说明车流量数据与客车占比数据均具有日周期性的特征,其中客车占比数据是交通流量数据中隐含的周期性部分。
2 预测模型的建立
2.1 LSTM的原理介绍
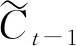
(4)
(5)
(6)
(7)
(8)
Ht=Ot×tanh(Ct-1)
(9)
式中:sigmoid函数是输入门 、输出门 、和遗忘门的激活函数,为双曲正切函数。
2.2 模型的预测性能评价
采用均方根误差(RMSE)、均方误差(MSE)、平均绝对误差(MAE)和平均绝对百分比误差(MAPE)来评价模型的预测性能。RMSE、MSE、MAE和MAPE的计算公式如式(10)~式(13):
(10)
(11)
(12)
(13)
式中:MAPE为相对误差,代表模型的适用程度; RMSE、MSE和MAE为绝对误差,其值越小,说明预测值和真实值越接近,模型效果越好。
2.3 交通流预测的整体流程
基于高速公路样本数据采用长短时循环神经网络(LSTM)训练构建高速公路的短时交通流预测模型。其总体流程为:①数据预处理剔除异常值;②利用FFT对流量数据及客车占比数据进行周期性验证;③利用LSTM对交通流量进行预测;④在流量数据中引入客车占比特征对流量进行预测;⑤模型评估,得出最优预测模型。其整体流程见图6。
3 实例分析
以广州市北环高速公路某收费站2015年12月14日—2015年12月20日共计一周的车流数据进行短时交流预测分析,其中有效数据为182 539条,选取其中122 301条作为训练样本,其余60 238条作为测试样本。
3.1 基于LSTM的短时交通流预测
3.1.1 LSTM模型搭建及参数选择
基于归一化数据搭建LSTM模型,t为时间间隔,Nt为t时段车流量数。将t时段收费站的车流量作为模型的输出,将此收费站t时段前的r个连续时间序列车流量值作为模型的输入,总体的输入输出模式如图7。图7中,虚线框为一个训练样本,箭头指向为此训练样本的标签。选择合适时间步长、网络层数、各层节点数使模型拥有良好的性能。为了使模型具有较强的泛化能力,在每次做时间步长调整过后,需要对训练集利用随机函数将数据块完全打乱,使得最大化地降低块与块之间的关联性,增强预测的合理性和准确性。
试验中的网络构建采用Keras框架实现LSTM模块。通过交叉验证的试验发现,采用2层LSTM构建的循环神经网络,时间步长为4时,模型具有良好的表现力。模型采用随机梯度下降(stochastic gradient descent, SGD)的方法进行优化,学习率为0. 001,批处理大小为128,最大迭代次数为5 000。
3.1.2 引入客车占比特征的改进模型
根据1.2.2节对高速公路收费站车流量数据和其客车占比数据的周期性验证可知,客车占比数据是交通流数据中隐藏的周期性部分。类似于此的周期性数据有利于提高模型预测的准确度,故而在t时间间隔内的输入特征中引入客车占比。改进后的输入输出模式如图8。同时,为使实验结果具有可比性,引入客车占比特征后依然运用2层LSTM神经网络进行预测,采用随机梯度下降进行优化,学习率为0.001,批处理大小为128,最大迭代次数为5 000。
3.2 实验结果
3.2.1 实验1
根据3.1.1节的预测模型,分别选取时间间隔t为5、10、15 min,选取r=4,即利用前4个时间序列的高速公路收费站车流量数据,预测第5个时间段的车流量。3个不同时间间隔的模型预测结果如图9,3个不同时间间隔的预测误差如表3。由表3可以看出: 3个时间间隔的预测模型的MAPE均在20%以下,说明模型有较好的适用程度;当时间间隔选取5 min时,预测模型的均方根误差(RMSE)、均方误差(MSE)和平均绝对误差(MAE)分别为1.27、1.61和9.95,模型的预测效果最好。同时,为了比较算法的优劣程度,分别利用ARIMA算法、BP神经网络对同样的数据进行训练及预测,各类算法预测误差的比较结果如表4,其中LSTM算法的误差最小,预测效果最好。
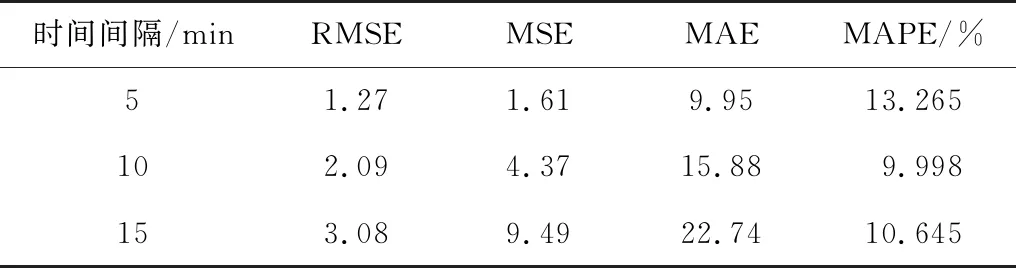
表3 不同时间间隔下算法的误差
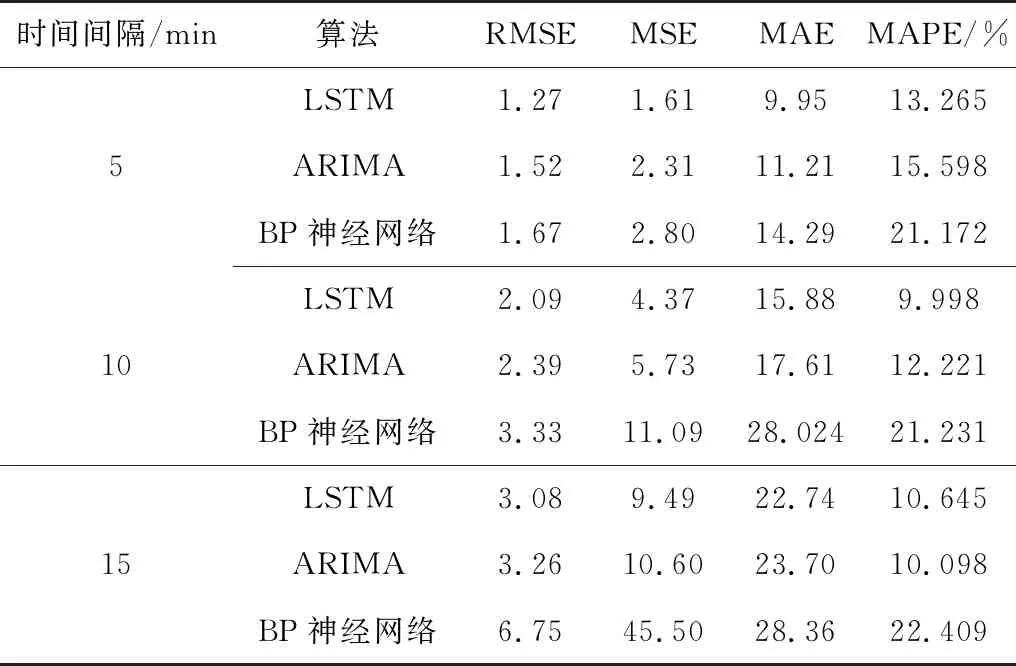
表4 各类算法误差比较
3.2.2 实验2
基于3.1.2节,对输入样本增加客车占比特征,同时选取与未加此特征时相同的t与r。模型预测结果如图10。不同时间间隔下算法的误差如表5。对比表3和表5可知:引入客车占比特征后,相同时间间隔下预测模型的RMSE、MSE与MAE均减小,且当时间间隔为5 min时,预测模型的RMSE、MSE与MAE分别为1.16、1.35和9.07,分别下降了0.11、0.26和0.88,说明引入客车占比特征可以有效减小模型误差,提高预测准确率。
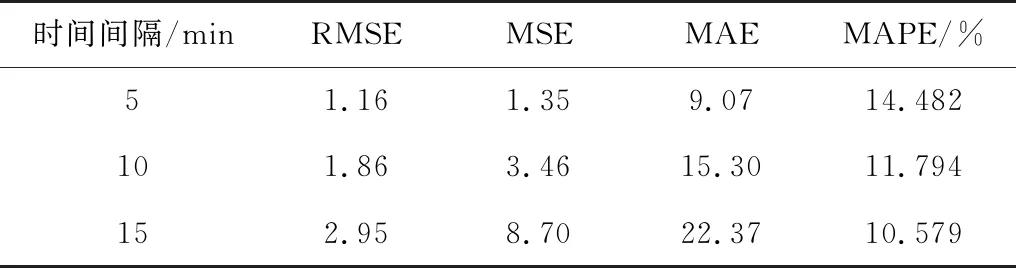
表5 引入客车占比后不同时间间隔下算法的误差
3.2.3 小 结
对实验1和实验2进行比较,可得:当时间间隔选取为5 min时的模型预测结果最为优越;加入客车占比特征后,模型预测误差减小,准确度提高。
4 结 语
以高速公路收费站的车流数据为基础,引入客车占比特征,利用LSTM神经网络构建高速公路短时交通流量预测模型。提取车流数据中的客车占比特征并利用快速傅里叶算法(FFT)绘制功率频谱图对其进行有效的周期性验证,证明其是高速公路收费站车流量数据中隐藏的周期性部分。通过在模型中引入此特征,并选取适当的时间间隔,降低了模型的预测误差,提高了短时车流量预测的正确率。
