基于粒子群优化算法的冗余机械臂运动学逆解

石建平

(贵阳学院 电子与通信工程学院，贵州 贵阳 550005)

机器人的逆运动学求解是指已知末端执行器相对于参考坐标系的位置和姿态，求机器人末端执行器到达给定位置和姿态所需的各关节变量值。机器人运动学逆解运算本质上是一个复杂非线性方程组的求解，该问题是机器人学领域的一个技术难题，同时也是研究机器人动态特性分析、轨迹规划和运动控制的基础与前提。求解运动学逆解的传统方法有封闭解法和数值解法。[1]其中封闭解法可根据公式或几何构型直接推导出关节变量表达式，该方法计算速度快、精度高，且能求出所有可能逆解，但封闭解法只能求解结构构型满足Pieper准则[1]的简单机器人的逆运动学问题，其通用性不强。数值解法是冗余机器人逆运动学求解的主要方法，典型的数值解法有基于雅克比矩阵的迭代法，迭代法需要对雅可比矩阵进行求逆运算，其实现过程繁杂，不易编程实现且存在奇异性问题。

近年来，粒子群优化算法[2-7]、差分进化算法[8,9]、遗传算法[10,11]、类电磁机制优化算法[12]、萤火虫群算法[13]、人工蜂群算法[14]等智能优化算法被应用于机器人的逆运动学求解，研究进展其情况较好。基于智能优化算法的机器人运动学逆解求解方法不受机器人机构构型的限制，具有很强的通用性，很好克服了传统求解方法的不足，为解决机器人逆运动学问题提供了有效的解决方案。粒子群优化算法(Particle Swarm Optimization，PSO)[15]是Kennedy和Eberhart受鸟群群体觅食行为的启发而提出的一种群智能优化算法，该算法由于结构简单、控制参数少、易于实现等优点而受到广泛关注与研究。为改善粒子群优化算法的优化性能，文献[16]提出了一种综合改进的粒子群优化算法(Improved Particle Swarm Optimization，IPSO)，该算法已经成功用于解决混沌系统的参数估计问题。本文以平面冗余机械臂为研究对象，将IPSO算法用于机械臂运动学逆解的求解，进一步拓宽该算法的工程应用范围。

1 运动学方程与目标函数

1.1 运动学方程

本文采用的平面冗余机械臂如图1所示，以机械臂的基底为参考坐标系，则有如下的运动学方程:

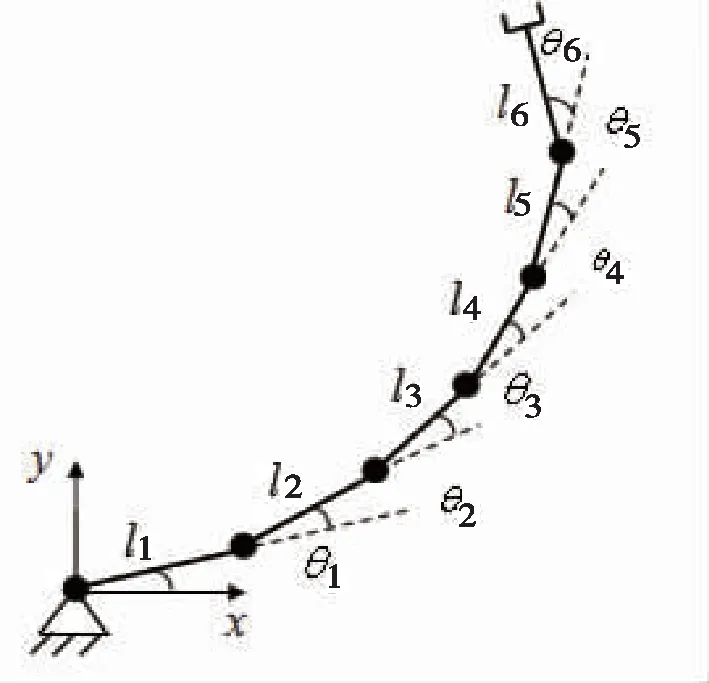
图1 冗余机械臂

(1)

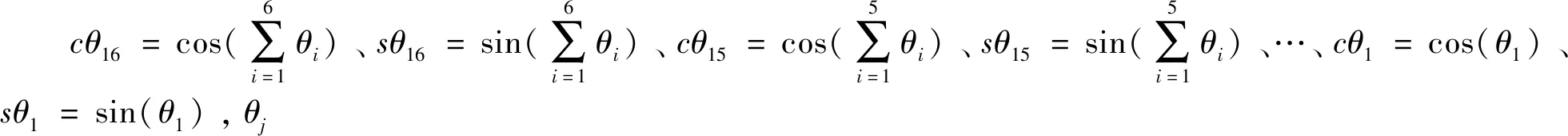
1.2 优化目标函数

由于从机械臂末端执行器的工作空间到关节空间的变换是一对多的映射关系，同一个末端执行器的位姿将有多个逆解与之对应。于是，如何从多解中选择一个比较适合的逆解成为不可回避的问题。为解决运动学逆解的选择问题，除了机械臂末端的位姿要求，通常还需要考虑机械臂从初始位置运动到目标位置的能量消耗、柔顺性和安全性等指标，这就涉及运动学逆解的约束优化求解。本文在机械臂的逆解运算中，将结合末端执行器的位置误差和机械臂关节运动的能量消耗两个性能指标来指导逆解的选择。

(2)

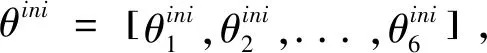
(3)

式中，θ=[θ1,θ2,...,θ6]。

实际应用中，追求机械臂末端执行器的位置精度为零是不现实也是不必要的，合理的选择应该是在位置精度满足实际需求的前提下使其运行成本更低。因此，以位置误差满足指定精度要求为约束条件，以机械臂从初始位置运动到目标位置过程中的能耗最小为优化目标。于是，可将机械臂的逆运动学问题转换成式(4)的最小约束优化问题来解决。

(4)

s.t.g(θ)=Δ-Δmax≤0

式中，Δmax为最大位置误差。

用罚函数法将上述约束优化问题(4)转换为无约束优化问题进行处理，采用的约束处理方法如下:

minf′(θ)=min(f(θ)+φ(θ))

(5)

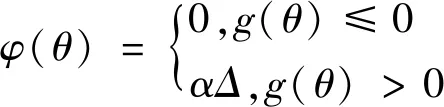
(6)

式中，f(θ)为原目标函数(即能耗最小优化目标函数)，φ(θ)为罚函数，f′(θ)为使用罚函数φ(θ)修正后的目标函数，即惩罚适应度函数，α为惩罚系数，其余参数与前述相同。

根据式(6)，机械臂末端执行器的位置误差越大，则对原目标函数的惩罚力度越大。

2 用IPSO求解机械臂运动学逆解

在用IPSO算法求解机械臂逆运动学问题中，粒子i由上述的6个关节角变量构成，即粒子i的位置向量表示为θi=[θi1,θi2,θi3,θi4,θi5,θi6]，其中θij(j=1,2,...,6)为各关节角变量，每个位置向量代表逆运动学问题的一个候选逆解；粒子i的速度向量用vi=[vi1,vi2,vi3,vi4,vi5,vi6]表示。根据参考文献[16]，用IPSO算法求解机械臂运动学逆解的详细步骤如下：

Step1参数设置与初始化，设置粒子位置与飞行速度的范围、种群规模m、最大进化迭代次数kmax、用式(7)-(9)对种群进行混沌初始化。

(7)

(8)

(9)

式中，uθ(j)、lθ(j)分别为粒子的第j维位置分量的上边界值与下边界值；uv(j)、lv(j)分别为粒子的第j维飞行速度分量的上边界值与下边界值；xn、yn是分别由式(8)和式(9)产生的混沌序列，其迭代初值要求不为零。

Step2 计算粒子i(i=1,2,...,m)的适应值f′(θi)，将粒子的初始位置设置该粒子i的历史最佳位置，将种群的初始最佳位置设置为种群全局历史最佳位置；设置i=1、k=1。

Step3 按照式(10)、式(11)更新粒子i的各速度分量和位置分量，用式(7)-(9)对粒子i的越界分量进行处理。

(10)

(11)

式中，ω为惯性权重，且ω∈[ωmin,ωmax]；c1和c2为学习因子；r1、r2和r3为[0,1]内均匀分布的随机数；pij(k)为粒子i所经历的历史最佳位置向量pi的第j维分量；gj(k)为整个粒子种群所经历的全局历史最佳位置向量g的第j维分量；k为当前进化代数，kmax为算法最大迭代次数。

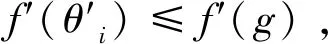
Step5 若i=m，执行Step6；否则i=i+1，返回Step3继续更新下一个粒子的速度和位置。

Step6 对粒子种群执行差分变异进化操作，设置i=1。

Step6.1按照式(12)得到粒子i对应的变异向量u(k)，参照式(7)-(9)对越界现象进行处理。

u(k)=g(k)+F(g(k)-pi(k))

(12)

式中，F为[0，1]内的缩放因子。

Step6.2 若f′(u)≤f′(pi)，则pi=u；若f′(u)≤f′(g)，则g=u。

Step6.3 若i=m，执行Step7；否则i=i+1，返回Step6.1继续执行差分变异进化操作。

Step7 从当前种群中选择适应值最差的粒子i进行局部变尺度深度搜索，设置k′=1。

Step7.1 根据式(13)更新适应值最差粒子i的位置。

(13)

Step7.2若f′(θi)≤f′(pi)，则pi=θi；若f′(θi)≤f′(g)，则g=θi。

Step8 若k=kmax，则算法寻优过程结束并输出寻优结果；否则k=k+1、i=1，返回步骤Step3继续下一代的迭代操作。

3 仿真实验与结果分析

3.1 参数设置

为检验IPSO算法求解机械臂运动学逆解的可行性与有效性，将IPSO算法的求解结果与PSO[15]、PSOTD[17]、PSOd[18]算法的求解结果进行对比分析，所有算法采用Matlab R2013a进行编程，计算机配置为：Intel Core(TM)i7—7700、3.6GHz、16GB内存、Windows 10操作系统。

3.2 实验结果与分析

将各算法分别独立连续进行100次逆解运算，各算法寻优结果的最优适应值(Best)、平均适应值(Mean)、最差适应值(Worst)及标准差(Std.)分别如表1所示，各算法对应的最优逆解结果如表2所示，各算法对应的最差逆解结果如表3所示，各算法的平均适应值收敛曲线如图2所示。

表1 不同算法的逆运动学优化求解结果

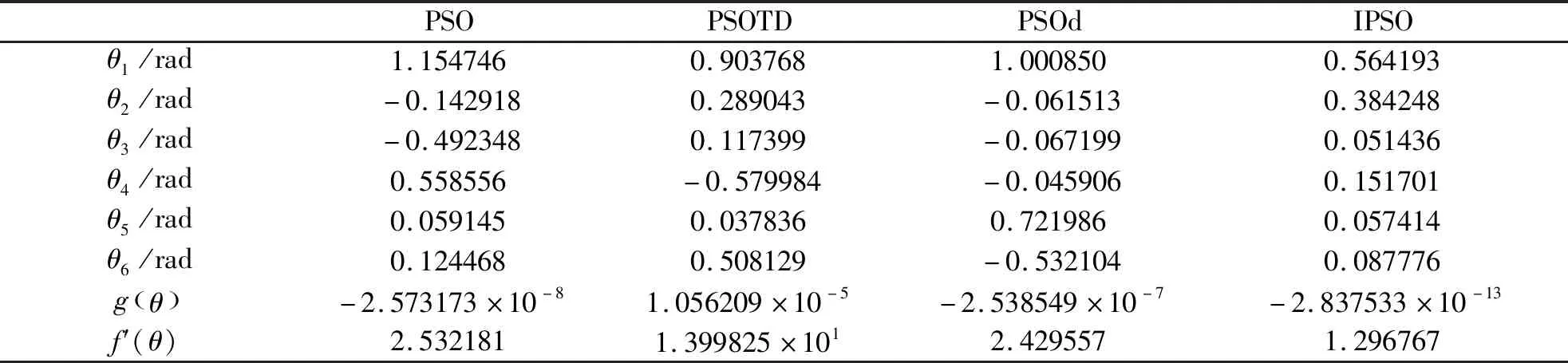
表2 不同算法的最优运动学逆解

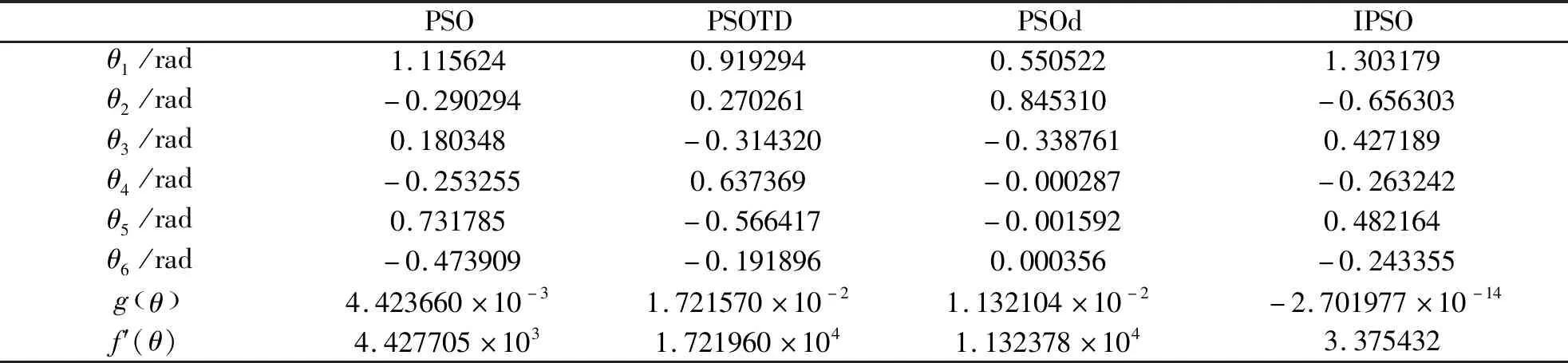
表3 不同算法的最差运动学逆解

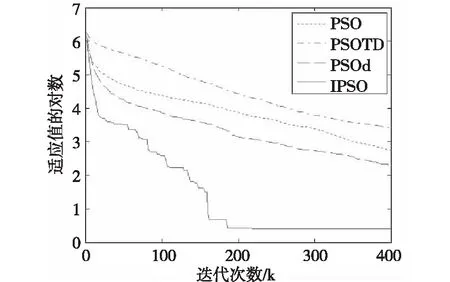
图2 不同算法求解机械臂运动学逆解的平均收敛曲线

根据表1的寻优结果可知，IPSO算法的最优适应值、平均适应值、最差适应值及标准差都明显优于PSO、PSOTD及PSOd算法，IPSO算法能够在满足给定约束条件的前提下对逆运动学问题进行寻优求解；根据表2，PSOTD算法的最优逆解结果违反了给定的约束条件，而PSO、PSOd及IPSO算法的最优逆解结果都能够满足给定的位置精度要求；根据表3的最差逆解结果可知，除了IPSO算法外，其余算法的寻优结果都违反了约束条件；在图2中，IPSO算法的平均适应值收敛曲线下降速度最快，并获得了最低的下降位置，说明与其他算法相比， IPSO算法具有收敛速度快、收敛精度高的优势。

综上所述，在机械臂运动学逆解的约束优化求解中，IPSO算法在4个算法中获得了最好的求解质量，可用于有效求解机器人的逆运动学问题。

4 结论

本文将机器人的逆运动学问题转换成一个等效的最小约束优化问题，并利用粒子群优化算法来对该问题进行有效求解。这种基于群智能优化算法的机器人运动学逆解求解方法具有很强的通用性，对机器人的机构构型没有特殊要求，可用于求解一般机器人的逆运动学问题。以平面冗余机械臂为例，对PSO、PSOTD、PSOd及IPSO算法在运动学逆解运算中的有效性展开试验对比分析，仿真结果表明：与PSO、PSOTD及PSOd算法相比，IPSO算法获得了最好的求解质量，其运动学逆解对应的机械臂末端执行器的位置精度均符合约束要求，是一种有效的逆运动学问题求解方法。