数据挖掘评估中融合多目标决策算法应用研究

陈 辉

(淮南职业技术学院,安徽 淮南 232001)

1 多目标决策评估框架

在方法评估过程中设计了三个阶段：数据挖掘阶段，将收集得到的数据集进行预处理后，并从中挖掘出潜在价值数据，此时就需要从经典分类算法中初始化评估结果；多目标决策阶段，根据优化得到的权重值计算方式分析不同决策方法来获取得到分类算法的评估结果值，以此来提升决策精确性和可信度；二次挖掘阶段，基于多目标决策阶段更深层次的获取得到潜在价值数据。框架设计如图1所示。

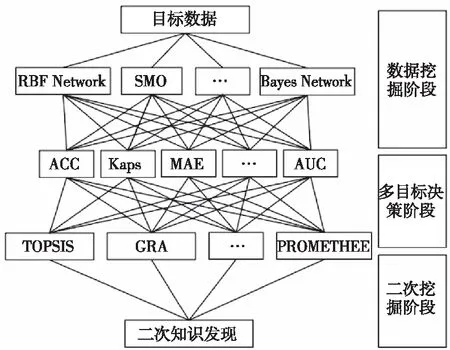
图1 评估框架图

2 优化AHP权重算法

AHP是经典的多目标决策方法，它分解复杂问题为简单问题，并通过专家对不同问题之间的关系进行决策结构的打分，并以此来构成两两判断矩阵，并在经过了计算后得出最佳方案的权向量，由此可知在当前的最佳方案判断中最为重要的则是决策指令的发出。[1]决策指令受到了专家个人背景以及知识构成等各个方面的影响，因此单一的决策缺乏科学性。[2]群决策理论则能够充分融合多个领域的专家理论知识，避免了决策过程中个人因素的影响，由此文章提出了在AHP中融合专家知识和领域知识的优化算法，提升决策的客观性和科学性。

2.1 AHP算法

AHP算法的决策流程主要包含以下几个步骤：

(1)确定层次目标。将复杂分体分解为简单问题，并提出层次目标。

(2)构建决策层级结构。将得出的层次目标按照某些规则分解为不同层次结构，如图2所示。

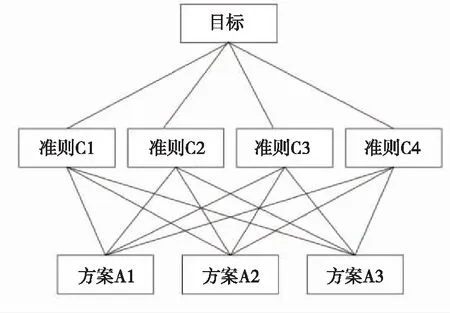
图2 决策层级结构

(3)构造两两矩阵。通常专家在各个层次结构中元素以及属性重要性进行打分后，并基于此得出每个属性的标度，从而构造两两对比矩阵。[3]属性重要性程度确定基本是根据1—9标度表，如表1所示。

表1 1-9标度表

由此可以获取得到两两对比判断矩阵：

A=(aij)n×n

上式中aij为元素ui,uj的重要性标度值，且它具备以下性质：

(4)层次排序。从两两判断矩阵A就可以获取得到权重值W=(w1,w2,...,wn)，并将其表示为向量形式w=(w1,w2,...,wn)，并由此应用特征根法来计算求解A特征根问题[4]：

AW=λmaxw

上式中λmax则是A的最大特征根。

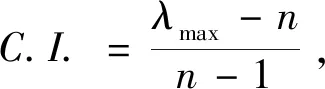
(6)层次总排序。将计算得到的权重值进行综合分析，并从下而上逐层判断一致性检验，由此就可以得到方案设计。

2.2 AHP群决策方法

AHP算法主要单个专家对判断矩阵的决策，而在解决具体的实践问题时则会由于专家个人学识、经验等各个方面差异性，这就会导致评估结果存在主观性。AHP群决策算法则是综合多人进行决策，并取平均值作为矩阵权重，这就具备较好的客观性和科学性。

AHP群决策算法的关键之处在于要结合单个专家的个人意见，以此来形成群体共识。文章应用目前较为常见的方式则是应用集结个体判断矩阵或个体排序来计算得到群排序，集结方式采用数据模型：

2.3 优化AHP权重方法

分别应用个体判断矩阵、个体排序集结方式得出判断矩阵时，两种方式存在内在联系，由此提出了专家权重的定量化研究，且在判断群决策矩阵中使用最小二乘法来优化AFP的权重计算过程，具体如下：

(1)构建初始判断矩阵Ak=(aij)m×m。设有k(1≤k≤n)个专家，每个专家都基于表1进行打分，以此来获取得到元素的评分值，由此可以得到初始化判断矩阵。

(2)计算专家权重。传统的权重计算方式均采用主观方式，这就会导致判断矩阵的主观性很强，由此设计专家权重的定量化计算方式。设当前已经得到了k个专家的权重打分值，且获取得到得矩阵数量为t(1≤t≤T)，且λk表示为当前第k个专家得出打分值，定量化计算过程如下：

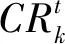
②确定初始化专家权重。在当前研究理论中可得知一致性比率取值区间为(0，0.1)，设计的初始化专家权重λk计算方式为：

当前研究理论可知，当α=10时具备比较好的系统稳定性和区分效率。

B=(λ1A1+λ2A2+…+λnAn)=(bij)m×m

(4)优化群决策判断矩阵。传统的群决策判断矩阵是通过算术均值法计算获取的，该种方式下计算得到群决策判断矩阵体B的互正反矩阵属性无法得知，因此设计了最小二乘法来改进群决策判断矩阵体B，以此来获取得到较为精确的判断矩阵B*，详细过程为：

确定最小二乘的数学规划问题：

根据AHP群策判断矩阵特点，将上述目标函数调整为：

s.t.xij>0(1≤i≤m,1≤j≤m)

并将上述问题划分为子问题：

s.t.xij>0(1≤i≤m,1≤j≤m)

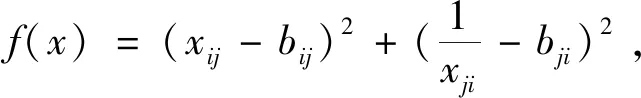
通过计算后可得到：

以此求解得到满足f(x)的所有最小值正解值。

(5)排序备选方案。

3 分类评估算法

决策树是一种树形结构的预测分析模型，它映射了数据对象和其属性值之间的关系。[5]它具有树的结构，由根节点、分支节点、叶子节点构成；根节点位于顶端；分支节点是上一节点判断后新的属性；叶子节点无法在进行判断，是树的判断结果。决策树的主要优势为简单、直观、 分类效果较好。较为经典的分类方法有贝叶斯网络、C4.5决策树算法、ID3决策树算法、逻辑回归、朴素贝叶斯算法等，文章以C4.5决策树和ID3为例进行详细介绍。

3.1 C4.5 决策树

C4.5决策树算法使用信息增益或熵降低的概念来选择最优划分[6]，从而以此来更好地实现构造决策树：

(1)属性列的选择依据为信息增益率；

(2)树的剪枝过程发生在树的构造过程中；

(3)对于连续属性的数据应用离散化的方式来进行处理；

(4)对于非完整的数据也采用树的剪枝构造。

在C4.5算法中能够有效地处理离散化连续型的属性，具体的过程如下：

获取连续性属性的最小值，并将其存储在MIN中，同样地以最大值存储在MAX中；

②将[MIN,Ai]为区间值时与(Ai,MAX]两者计算得到的增益值进行对比；

③选定断点中的最大增益值记录为Ak，并把[MIN,Ai]、(Ai,MAX]设置为属性的区间值；

假设数据库中的每个变量都有两个不同的值A和B，该变量的概率分布为：

a:若P(A)=1,P(B)=0，则表示这个变量的值肯定是A，不可能是B；

b:若P(A)=0.5,P(B)=0.5，则需要计算平均信息量，并以此实现对最佳数据量的不确定性评估，即信息熵：

集合S中的属性A中存在V个不同的数据值，且用A将S划分为v个子集{S1,S2,...,Sv}，且Sj中已经包含了集合S，即Sj⊇S，并在划分时计算信息增益率：

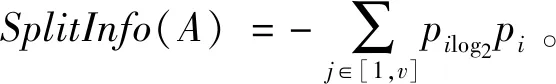
3.2 ID 3算法

ID3算法是自上而下通过训练属性中得最高信息增益，进而来构造决策树。因其总是选择最高增益信息的属性来划分规则，所以该算法分类速度快，树的深度平均，且划分规则简单。[7]

ID3算法的概念基础为：在构造决策树的过程中，非叶子节点映射非类别属性，节点分支映射属性值，叶子节点的生成路径映射了类别属性值；信息增益值最大的非叶子节点都将和剩余的节点相关联；熵用来表示非叶子节点的信息量大小。

ID3算法在构造决策树的过程中重要的是：属性确定、划分集合。确定属性的过程为从选取的数据中，选取增益信息值最大的属性作为根节点，并以该节点的属性值构造分支，将选取数据划分为几个互不相关的子集；非叶子节点分支后就将对子集值二次进行属性的确定，然后继续分支直至分支到叶子节点。

表2 ID3算法的主要思想

4 实验结果分析

实验数据集采用某银行信用卡数据信息，采用UCI机器学习得到，信用卡信息中主要包含了500个用户，变量有10个。其中信用差的用户有38%，剩余的则是信用好的用户。

在实验过程中要从经典的5种分类算法中评估选择一种最佳的分类方式，以此来提升挖掘信用数据的效率，具体流程如下：

(1)将收集得到的信用数据集进行预处理操作，包含了数据清洗、集成、转换等；

(2)采用五折较差验证方式训练和测试5个分类算法；

(3)各个专家采用应用以下多目标决策方法评估分类效率：TOPSIS、VIKOR、GRA，多目标决策方法评估的输入参数为(1)中得到的度量指标值；

(4)计算得到数据集下的初始排序结果值；

(5)计算各个多目标决策方法的权重值；

(6)输出优先级的最终排序结果值。

数据挖掘阶段计算得到的5个经典绩效指标结果值如表3所示。通过分析表3可知，每个分类算法都有最优结果值，因此在初始阶段中并较好的分类算法评估。[8]

表3 数据挖掘阶段数据集评估结果

接下来则应用多目标决策方法融合来评估分类性能，并在三种多目标决策算法的权重定义采用文章优化的权重计算方式，由此可得到多目标决策的分类方法排序，如表4所示。

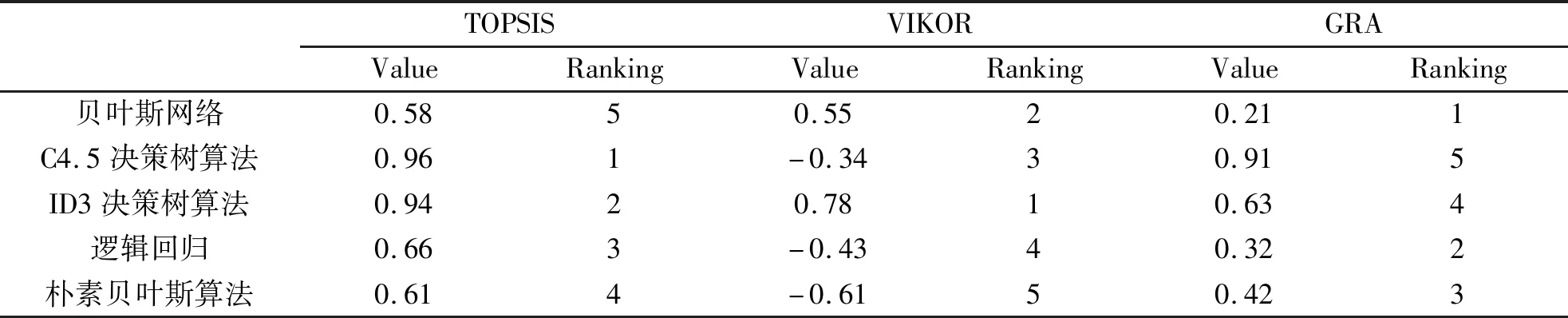
表4 多目标决策的分类算法排序

通过分析表4可知，在当前的多决策算法中TOPSIS具备较好的算法效率，并基于此可得到最终的分类效率排序结果如表5可知。

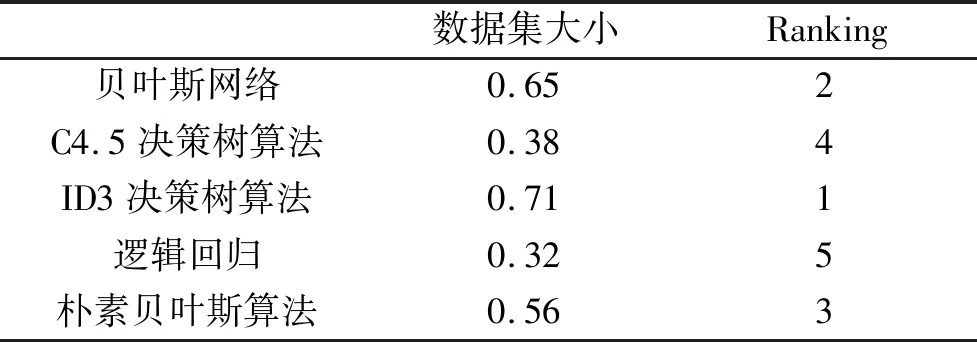
表5 最终排序结果

通过分析可知，数据集分析中排序值较高的为ID3决策树算法，这就表明在当前聚类分类算法中采用ID3决策树算法可以获取最佳的分类效率。

5 结论

AHP是经典的多目标决策方法，它分解复杂问题为简单问题，但单个专家的决策指令受到了专家的背景及知识构成等各个方面的影响，因此缺乏科学性。群决策理论则能够充分融合多个领域的专家理论知识，避免了决策过程中个人因素的影响，由此文章提出了在AHP中融合专家领域知识的优化算法，提升决策的客观性和科学性，在群决策目标中采用最小二乘法来获取最佳的权重值。