岭回归在消除多重共线性中的应用
2020-11-24林乐义
林乐义
(皖江工学院 基础部, 安徽 马鞍山 243031)
回归分析方法、回归算法以及回归模型,都是现阶段统计学的重要组成,回归分析作为一个重要的统计分析技术,其使用率高、应用范围广。利用该技术建立数学模型,表达数据之间的相互关系时,由于模型中解释变量之间存在高度相关关系,令该数学模型估计失真,以此需要通过消除多重共线性,实现数学模型的精准估计。多重共线性也可称作多重相关性,指自变量之间存在线性相关现象,当自变量之间存在完全线性关系时,则自变量之间的相关性绝对值为1;当自变量之间完全没有线性关系时,自变量之间的相关性为0。上述说明的是2种极端的自变量线性相关关系,通常来说,目前极易出现的是线性程度不同的相关现象,自变量之间的相关性绝对值在0到1之间变化。
针对回归分析的多重共线性问题,文献[1]提出岭回归中基于广义交叉核实法的最优模型平均估计方法,在存在异方差的背景下,考察了组合不同岭参数下岭估计量的模型平均方法,并在广义交叉核实法的框架下构造了相应的权重选择准则,使用蒙特卡洛模拟考察了所提出的模型平均方法在有限样本下的有效性,利用该方法对一组乙炔反应工艺的数据进行了分析,所得到的结论进一步表明,模型平均法在实际数据分析工作中具有较高应用价值。文献[2]提出部分线性变系数模型的约束岭估计方法,该方法研究了部分线性变系数模型在线性部分存在多重共线性和参数分量附加约束条件时的估计问题。基于profile最小二乘估计和岭回归估计方法,构造了参数分量的约束profile岭估计,并研究了其性质。但是以上2种方法的多重共线性处理效果较差,导致得到的回归系数不贴合实际。
针对上述方法存在的问题,本文提出全新的处理方法。该方法利用岭回归修正解释变量之间的多重共线性,并通过筛除重复度高、相似性强的自变量,消除多重共线性,得到的回归系数更贴合实际,为回归分析技术的改进和发展,提供有效的技术支持。
1 岭回归在消除多重共线性中的应用
1.1 确认多重共线性的影响程度
在投入岭回归消除多重共线性的方法中,需要预先确认多重共线性的影响指标。该影响指标就是存在大量精确相关关系或高度相关关系的解释变量,影响模型估计精准程度的指标[3-4]。已知建立一个多元线性回归模型需要一定条件,即回归模型外生变量组成的设计矩阵,为列满秩矩阵,同时该模型要求列满秩矩阵W的秩表现为F(W)=b+1,说明矩阵列向量之间不存在不全为零的b+1个数,用n0、n1、n2、…、nb表示,则有:
n0+n1xi1+n2xi2+…+nbxib=0
(1)
上式中:i=1,2,…,m表示数量;x1、x2、…、xb表示分析模型的外生变量。此时的外生变量x之间存在严重的线性关系[5]。当变量之间的共线性程度较强时,设回归模型为:
y=β0+β1x1+β2x2+…+βbxb+k
(2)
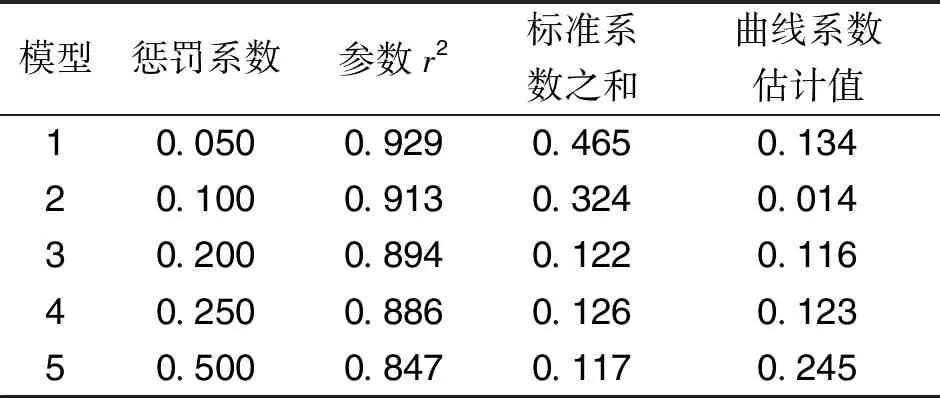
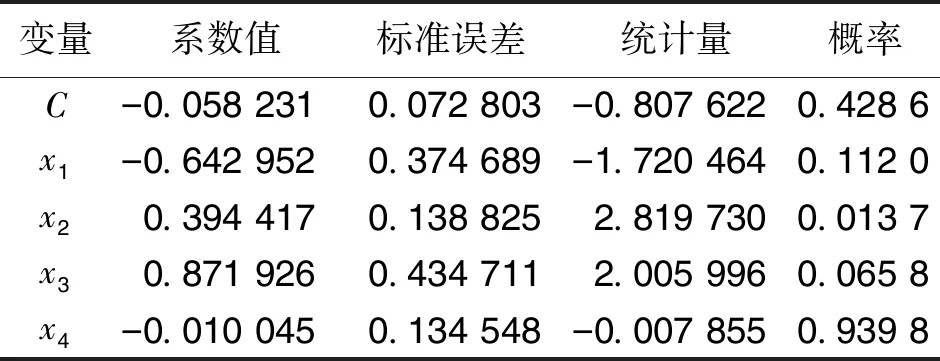
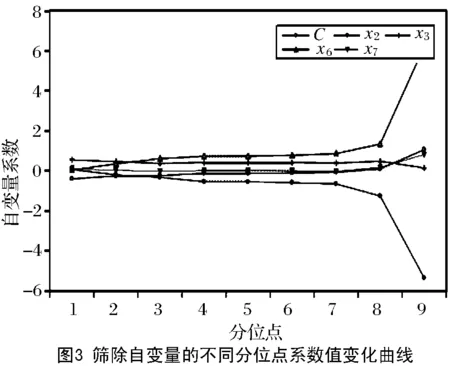
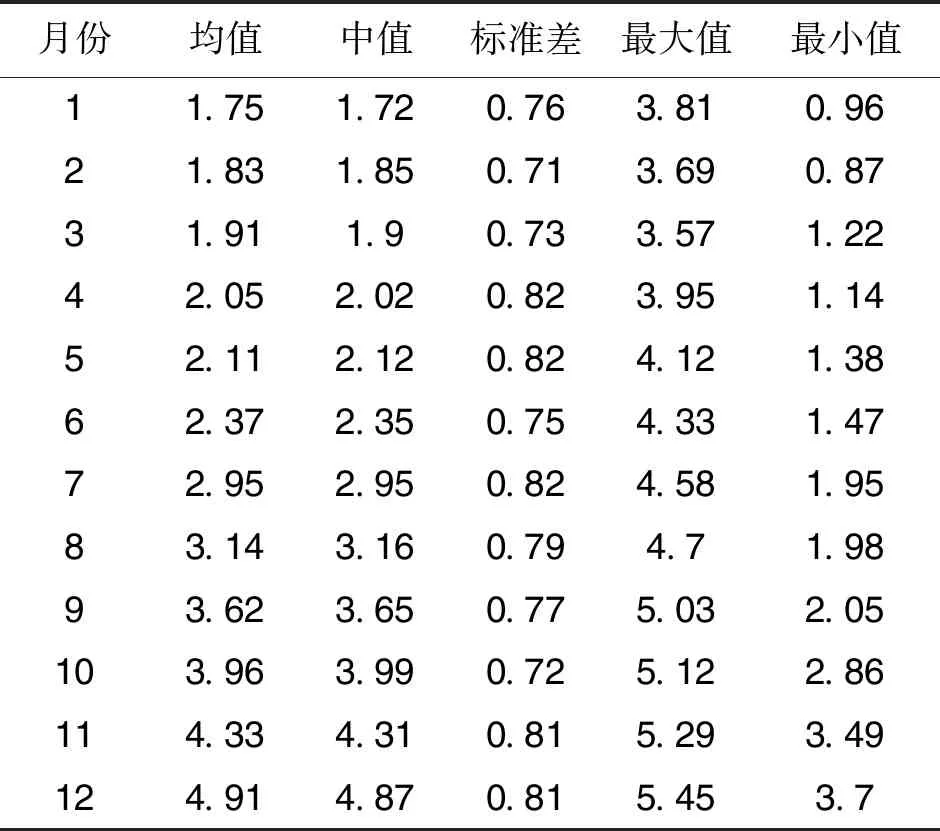
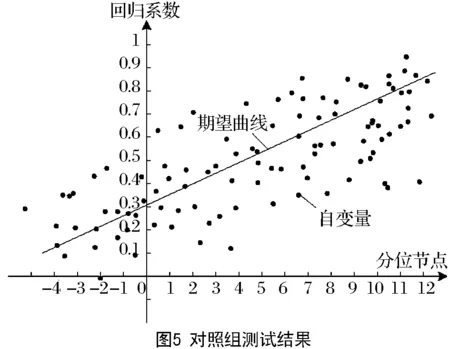
式中:β0、β1、β2、…、βb表示与分析模型外生变量xb相对应的回归系数;k表示固定常数。当上述模型的解释变量之间存在公式(1)的状况时,矩阵W的秩F(W) 根据上图可知,外生变量的发生概率随着模型参数的增加而提升。因此假设1个多元线性回归模型内存在2个外生变量,此时的回归模型可设置为二元化模型,计算公式为: y=β0+β1x1+β2x2+k′ (3) 式中的k′为二元化模型下的固定常数。外生变量x1与x2具有完全共线性;若x2=μx1时,μ为变量控制参量,此时的二元线性回归模型,可变为简单一元线性回归模型: y=β0+(β1+μβ2)x1+k′ (4) 上述模型可以对(β1+μβ2)的取值进行估计,但并没有办法确定β1、β2各自的估计值[7]。此时的回归模型完全失去统计分析意义,模型多重共线性非常严重。计算多重线性与模型真实值之间的差异指标: (5) 上式中:g(*)表示预测函数;f(*)表示评估函数;σ表示对β值的约束参量;η、η′是对W、W′的限制条件标准值;d表示差异指标。当d值为正时,说明多重线性对模型的影响较弱,消除多重共线性只需利用岭回归即可;当d值为负时,则说明多重共线性严重,需要调整岭回归的k值[8]。 图中的rx1~rx9表示岭迹分析曲线,根据曲线走势可知,不同的k值会直接影响岭迹曲线,因此需要计算2种情况下的岭估计量k值。一种是普通岭估计量值, (6) i=1,2,…,c. (7) 上式中k2表示广义岭估计的k值。需要注意的是,无论是普通岭估计结果还是广义岭估计结果,在获取岭回归k值时,都要按照实际目标来选择。根据全新的k值改进岭回归方程,改进后的公式为: (8) 公式中:W′、W为已知的矩阵和转置矩阵,y为上述公式所求的线性回归方程;k表示公式(6)、(7)获取的k值;s表示修正系数;△T表示需要剔除的计算偏差[11]。综合上述所求,获得取值不同的岭回归k值,实现对岭回归方程的优化改进。 根据改进后的岭回归进行分析,以解释变量是否具有线性相关性为分析依据,将解释自变量划分为2个部分,实施对回归模型的区别分析。该分析需要筛除自变量,以此达到对多重共线性全面消除的目的。岭回归标准化处理数据,比较标准化岭回归系数,选取自变量,设置步长为a的岭迹表,并绘制相应的岭迹图,结合k值确定自变量系数大小、常数项的取值范围。根据公式(8)选取岭估计曲线趋于平稳处的k值,已知经公式(8)计算,获得的步长为a的岭参数k值如表1所示[12]。 表1 步长为a的岭参数k值表 根据岭迹分析法可知,在初始阶段和分析末段,岭迹大致处于稳定,此时的k值更加符合计算要求。去掉岭回归系数集合中,相对来说较稳定、且绝对值较小的自变量xi,以及随着k值变化而快速接近于0的自变量x0,筛选后的自变量记为xj。检验剩余自变量的显著性,表2为显著性测试结果[13]。 表2 显著性结果 由于剔除自变量会损失模型中的有价值信息,因此根据上表中的显著性分析结果,对剔除后剩余自变量xj,进行分位数回归分析,保证剩余变量的可靠程度。当自变量的系数均为正数时,说明这些系数与因变量呈正相关关系,意味着待分析指标q1、q2、…、qn对因变量指标起到了促进作用,即因变量指标随着待分析指标qn的变大而增大。选取分位点r,对筛除自变量进行分位数回归,令r=0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,其中当r=0.8时的分位数回归参数,如表3所示[14]。 表3 r=0.8时的分位数回归 根据上表中参考数据,计算各个分位点回归方程的岭回归系数,得到图3所示的分位点系数值。 图中的x2、x3、x6、x7为筛除后的自变量。根据上图可知,在分位点0.1~0.7区间内,自变量的系数变化较为平稳;而0.7~0.8区间内,除了自变量x2的系数逐渐减小,其他系数均保持缓慢增长趋势;而在0.8~0.9阶段,自变量x2、x6的系数变化强度大,且方向相反,可知分析指标对因变量的影响是不同的[15]。在文献[1]所提出应用方法的基础上,结合岭回归实现对多重共线性消除的研究目的。 为验证岭回归的可靠性和适用程度,提出对比实验,将岭回归应用下的多重共线性消除方法,与文献提出的传统消除方法进行比较,分析不同应用下的多重共线性消除效果。 鉴于数据的可靠性和真实性,调查国家某一机构上一年度的销售指标,将该指标作为参考对象,已知该指标包含12个月份,具体数据如表4所示。 表4 实验测试指标 建立可靠度评估模型和数据预测模型,以此评估4种方法的多重共线性消除结果,可靠度模型为: r(x)=1-σk(w,v) (9) 式中:X表示消除结果;σk表示评估标准为k时的数据允许变化量;w表示支持度;v表示满意度。同时预测模型为: (10) 公式中:γ表示共线性结果;ε表示预测限制参量;n表示预测次数;φi表示共线性的有效参数。利用上述模型对应用效果进行检测,分析并得出实验结论。 将岭回归应用下的多重线性消除测试结果作为实验组,将文献[1]所提出的传统方法应用下的测试结果作为对照组,图4、图5为此次实验测试结果。 分析上述2组测试结果可知,岭回归筛除后的自变量集中分布在期望曲线2侧;而文献[1]提出方法,剔除后的自变量仍然呈分散状态,不与期望曲线有相关性,可见所提出方法下,岭回归可以更好消除多重共线性,得到的回归系数更贴合实际。 设定因变量y表示中国国民总收入,自变量x1、x2、x3、x4、x5分别表示就业人员数、财政收入、能源生产总量、国有单位工资总额和城镇集体工资总额。根据《中国统计年鉴》得到2010—2014年的相关数据如表5: 表5 相关数据 在SAS软件上,诊断出模型中存在非常严重的多重共线性问题,利用本文方法和文献[2]所提出的部分线性变系数模型的约束岭估计方法分别对多重共线性进行处理。 利用部分线性变系数模型的约束岭估计方法所得到的回归方程为: y=-431189+6013224x1-0.18088x2 +0.44051x3+5.69125x4-13.63786x5 (11) 利用本文方法所得到的回归方程为: y=-305467.46+4.315x1+1.50x2+0.264x3+4.535x4+1.388x5 (12) 根据公式(11)可以看到方程中,自变量x2、x5的系数为负,与事实不符,是由多重共线性所导致,因此部分线性变系数模型的约束岭估计方法求出的回归方程不利于模型的解释;而公式(12)可以看出,回归系数的符号符合实际意义,说明利用本文方法可以有效解决多重共线性问题。 引入岭回归消除多重共线性,通过了解多重共线性的影响程度,获取普通意义上和广域意义上的k值,确保筛除后的自变量可以保留基本价值信息,保证回归系数真实可靠。此次对岭回归的应用分析较为复杂,计算较为困难,今后的研究可以简化一些分析与计算过程。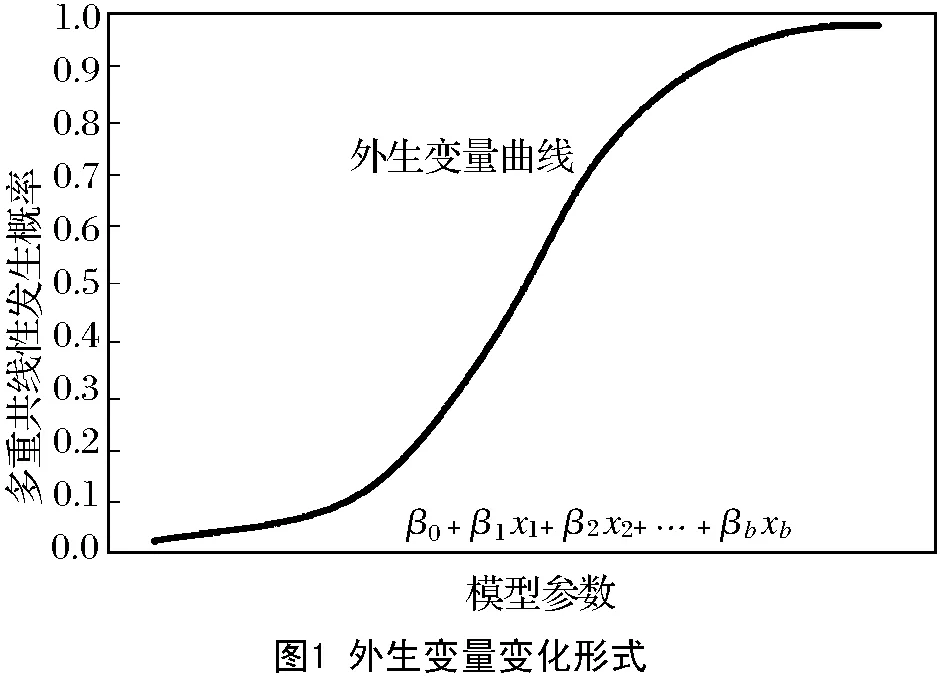
1.2 获取岭回归k值
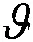
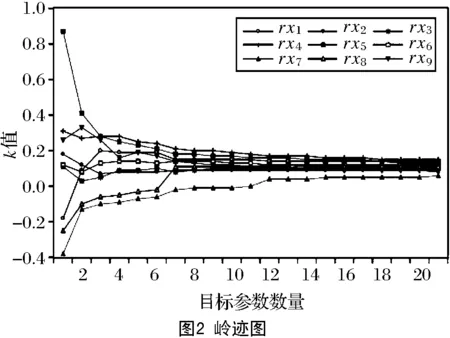

1.3 筛除自变量岭回归消除多重共线性

2 实验检测
2.1 实验准备
2.2 结果分析
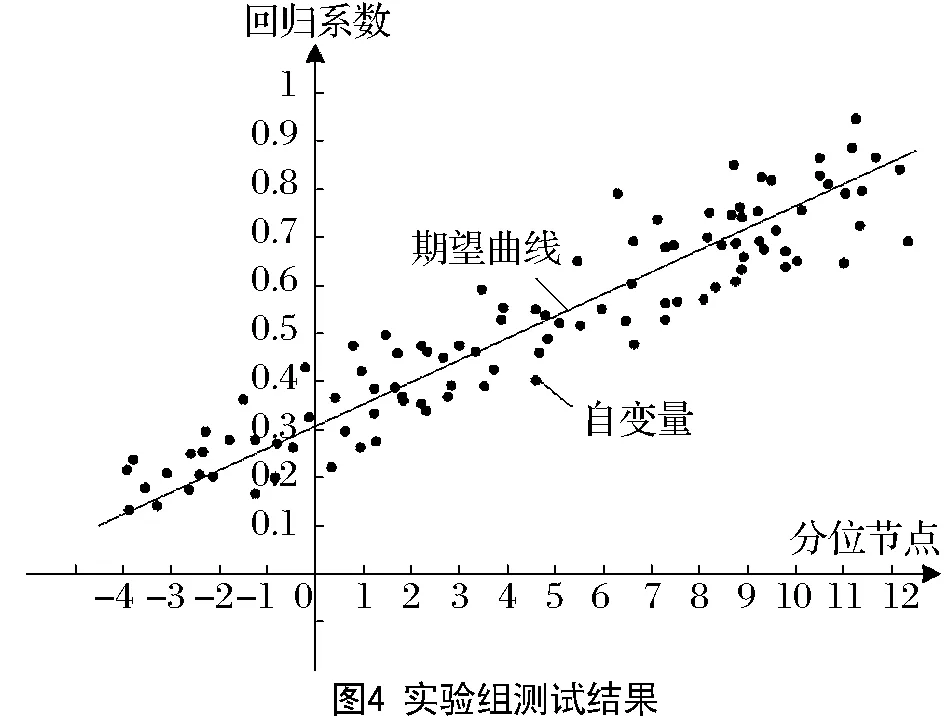
2.3 实例比较

3 结语
