非线性中立型时滞微分方程的振动性

寇 静

(太原工业学院 理学系，太原 030008)

非线性中立型时滞微分方程在2自由度控制系统和时滞系统设计中具有广泛的应用前景，对非线性中立型时滞微分方程的振动性进行分析，能够提高非线性中立型时滞微分方程的输出稳定性[1]，因此相关的非线性中立型时滞微分方程振动性分析方法研究受到人们的极大关注[2]。本文对稳态收敛条件下的非线性中立型时滞微分方程收敛性进行分析，通过双边稳定性分析方法实现非线性中立型时滞微分方程的振动性分析，最后通过验证得出有效性结论。

1 构造非线性中立型时滞微分方程

估计非线性中立型时滞微分方程的M-P广义逆矩，设x1(t),x2(t)为非线性中立型时滞微分方程双边界函数条件，研究非线性中立型时滞微分方程在双边界条件下的振动性[3]，在t→∞的情况下，根据非线性中立型时滞微分方程在双边界条件下的凸优化条件，得到非线性中立型时滞微分方程的松弛解代数方程组：

(1)

(2)

在线性子空间中进行方程特征分解和周期解分析。

定理1振动性泛函定理[4]。在非线性中立型时滞微分方程中，令r个整数m1,m2,…,mr两两互素，a1,a2,…，ar是任意r个非线性中立型时滞微分方程的特征分布集，则同余方程为x≡aimodmi(1≤i≤r)，得到非线性中立型时滞微分方程的特征分布矩阵：

(3)

利用平衡点平移特性，对振动特征解进行边界约束分析，得到了以下的边界函数：

p=-(fx1+gx2)|P0(x01,x02)

(4)

q=detA

(5)

M=m1,m2,…，mr，得到非线性中立型时滞微分方程的唯一解，其表达式为：

(6)

其中，Mi=M/mi，yiMi≡1modmi，1≤i≤r，所以在非线性中立型时滞微分方程解集中，采用高阶时频特征变换进行非线性中立型时滞微分方程解的模糊度寻优，得到核函数为：

K(xi,xj)=〈xi,xj〉

(7)

K(xi,xj)=(〈xi,xj〉+1)d

(8)

K(xi,xj)=exp(‖xi-xj‖2/2σ2)

(9)

上式中，核系数σ=0.707。

采用连续稳定性分析方法，进行非线性中立型时滞微分方程的模糊度分析：

(10)

上式经常用于有理数或者无理数的逼近，采用有理积分控制方法，进行非线性中立型时滞微分方程的输出振动性特征解分析。

2 微分方程的振动性分析和证明

在实数域中求得稳态收敛条件下非线性中立型时滞微分方程的连续格林函数的正多解，采用高斯混合边缘融合方法进行振动性特征解的非齐次边界性分析[5]，构建非线性中立型时滞微分方程的扰动特征泛函凸组合模型，分析其收敛性和振动性。

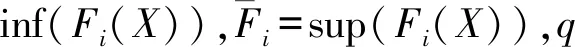
(11)

定义2非线性中立型时滞微分方程的决策函数F′(X)满足W(F(X))≤LW(X)，L是常数，则称F′(X)是Lipschitz区间函数，得到非线性中立型时滞微分方程的振动性特征解的可逆矩阵：

(12)

(13)

公式(12)与公式(13)表示非线性中立型时滞微分方程的振动性特征解的极大熵函数，此时在矩阵H中存在非线性中立型时滞微分方程的正交奇异特征解，表示为：

(14)

状态变量x(t)中的标量ξ和非零向量v满足系统稳定性[6]，得到方程特征解的正定矩阵的阶数为m，m-1列和第m+1列形成子方阵，表示为：

(15)

在实数域中求得的稳态收敛条件下非线性中立型时滞微分方程的连续格林函数D的正多解，采用高斯混合边缘融合方法进行振动稳定性特征解的非齐次边界性分析[7]，半正定矩阵A-1(A|B)=(E|A-1B)中存在奇异的m阶子方阵，得到非线性中立型时滞微分方程的联合特征函数为：

(16)

(17)

假设{qN}单调递增，qN≥1，得到非线性中立型时滞微分方程的扰动特征泛函为：

(18)

(19)

构建非线性中立型时滞微分方程的特征向量多项式，得到：

≤k‖W(x(k))‖∞

(20)

根据非线性中立型时滞微分方程的特征向量分析结果，对方程的收敛性进行证明。

当N→∞时，|x(k)|→0，得到非线性中立型时滞微分方程的特征解满足渐进稳定性，此时‖W(x(k))‖∞→0，由积矩阵Schur分解的扰动定理，得到：

(21)

(22)

得到非线性中立型时滞微分方程的振动性特征解为：

(23)

可知，根据Schur收敛性条件，得到非线性中立型时滞微分方程的振动解是渐进稳定的[9-10]。

3 实证分析

在实证分析中，取非线性中立型时滞微分方程的针振动系数ε=10-6，取x=(X1,X2) 为区间向量，目标函数为：

f2(x)=X1+X2+1,

f3(x)=sinX1-cosX2.

(24)

x(0)=[[-1,2][-1,2]]

(25)

p取0.3时，求解出非线性中立型时滞微分方程的稳定特征量x=(X1,X2)：

X1=[-0.4301597103476526,

-0.4301595991717815]

(26)

X2=[-0.5698403045535088,

-0.5698402933776378]

(27)

计算

KX(l)={k∈{1,2,…,n}|W(xk(l))≠0)}

(28)

非线性中立型时滞微分方程的凸组合模型为：

f(x)=[1.071539141671495,

1.071539141671497]

(29)

最后得到非线性中立型时滞微分方程的寻优曲线如图1所示。

分析得知，本文方法进行非线性中立型时滞微分方程振动性分析的寻优能力较好。

4 结语

对非线性中立型时滞微分方程的振动性进行分析，能够提高非线性系统的控制稳定性。本文利用采用高斯混合边缘融合方法进行振动性特征解的非齐次边界性分析，构建非线性中立型时滞微分方程的扰动特征泛函凸组合模型，分析其收敛性和稳定性，分析得出非线性中立型时滞微分方程的振动解是渐进稳定，且方程的振动性特征解具有边界性。