四辊轧机辊系刚柔耦合动力学建模研究
2020-11-24马兴旺孙建亮
张 阳,马兴旺,孙建亮
(1.太原科技大学 重型机械教育部工程研究中心,山西 太原 030024;2. 燕山大学 国家冷轧板带装备及工艺工程技术研究中心,河北 秦皇岛066004)
0 前言
轧机装配间隙以及辊系约束部件的动力学特性使得轧机系统各部件动态特性的产生成为可能。为了准确描述板带轧机系统空间动力学特性,需要针对板带轧机系统内部动态响应之间的耦合机理进行深入研究,完善轧机系统动力学模型体系,为实现板带轧机稳定运行奠定理论基础。
王桥医[1]从实际连轧组中采集多物理过程的表现状态与信息,对轧机系统的垂直振动进行测试分析,确定其振动机理和振源。张瑞成[2]利用相平面法和Poincare映射法分析了垂直振动系统的线性阻尼、外扰力和主传动系统的线性阻尼变化对轧机垂扭耦合振动的影响。杨旭针[3]对铝板高速轧制过程中频繁出现的冷轧机垂直振动现象,结合轧制工艺润滑原理和机械振动理论,建立基于辊缝动态摩擦方程的轧机垂直振动模型。Swiatoniowski[4-5]将轧辊视为Timoshenko振动梁,建立了板带轧机连轧过程高频振动模型。刘浩然[6]考虑轧件弹塑性变形的滞后非线性作用,建立了辊系滞后非线性垂直振动模型,为研究抑制轧机振动和保证轧机平稳运行提供了理论参考。孙建亮[7-8]曾将辊系看作双梁组合系统,分析了辊系的动态特性,考虑金属动态秒流量变化,建立了轧制过程动态模型。闫晓强[9-10]在轧机主传动系统机电耦合振动的研究中,考虑引起轧机传动系统强耦合振动的机电相互作用过程,建立了机械传动系统的等效非线性动力学模型。时培明[11]建立了含参激多自由度轧机传动系统非线性扭振动力学模型,分析了非线性扭振系统存在的复杂分岔结构和混沌运动。Drzymal[12-13]建立了轧辊打滑时轧机扭振非线性测量模型,分析不同轧制速度下产生稳定自激振动的方法。Tehrani[14]建立了冷连轧机耦合扭振系统测量模型,针对相邻机架间带钢张力和速度波动对轧机传动系统扭振的影响进行了研究。王瑞鹏[15]综合考虑轧机垂直振动、水平和扭转振动的耦合特性,建立了轧机耦合振动模型。杨旭[16]建立了冷轧机两自由度垂向系统非线性自激振动模型,利用奇异值理论分析了不同刚度、阻尼等非线性条件下系统的稳定性。张明[17-18]对某厂热连轧机F2机座进行振动测试试验,对振动过程进行仿真分析,研究轧机结构间隙、轧制力和摩擦负阻尼对轧机水平自激振动的影响,对于分析轧机振动对板带表面振纹的产生和厚度波动的影响具有重要意义。但这些研究在建模过程中,对轧机系统进行了大量的简化,模型不能真实地反映轧机系统各部件的运动特征,以及由于某些部件磨损引起的轧机状态波动。
本文以四辊板带轧机为研究对象,分别建立辊系刚柔耦合动力学模型;轧机系统刚性振动模型;轧制变形区耦合动力学模型。仿真分析轧制过程中轧机辊系和变形区内轧件的动力学特性、以及由于外界扰动和参数变化对产品质量的影响,为轧机运行稳定性分析和振动预测提供理论基础。
1 轧机辊系刚柔耦合动力学模型
轧辊常见的振动形式如图1所示,轧机辊系振动是由其系统内部复杂结构、外部载荷波动耦合作用引起的多源振动信号耦合。图2所示为四辊轧机辊系弯曲振动模型。

图1 轧辊常见的振动形式
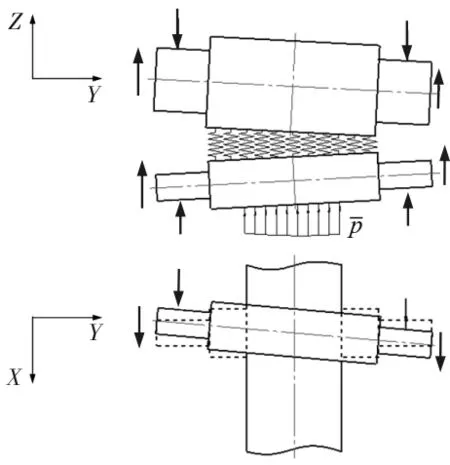
图2 四辊轧机辊系弯曲振动模型
如图2所示,辊系的运动包括支承辊、工作辊的刚性运动和弹性变形。考虑轧制过程中辊系操作侧和传动侧机械结构和液压压下系统动态响应的不同,基于轧辊沿Z方向和Y方向的动特性分析,研究轧辊沿X方向、Z方向的刚性运动和轧辊沿Y方向的弯曲变形运动之间的耦合关系。基于弹性梁变形理论,利用虚功原理,建立板带轧机轧辊刚柔耦合动力学方程

(1)
式中,r01、r02、r03分别为轧辊沿水平、垂直和轧制方向的刚性运动分量。因此,为了确定轧辊柔性变形的动特性,需要建立轧机系统刚性振动耦合动力学模型。基于文献[19]的研究成果,建立轧机系统刚性振动模型,为实现辊系刚柔耦合动力学建模奠定基础,如图3所示。

图3 轧辊空间刚性运动状态示意图
考虑轧机辊系的惯性与刚度耦合特性,采用集中质量法建立轧机系统刚性振动微分方程
(2)
式中,
2 轧制变形区耦合动力学模型
2.1 单位宽度轧制力增量
由图2可知,单位宽轧制压力的变化量直接影响工作辊的变形运动,通过分析轧件动态变形特性,基于轧制理论Orowan-Pascok公式,可得单位轧制压力表达式
(3)
式中,Qp为应力状态系数。
对式(3)求全微分,可得单位轧制压力动态增量表达式
式中,
整理分别可得工作辊、支承辊刚柔耦合运动微分方程
(5)
2.2 轧制变形区耦合动力学方程
轧辊在轧制过程中发生运动的同时,也会使轧件在变形区内产生横向周期运动。由本文分析可知,轧辊变形振动特性与轧件出口横向位移u(y,t)有关。基于文献[20]的研究成果,根据轧制过程的特点,同时考虑轧辊刚性运动和弯曲变形,构造满足轧制变形区横向位移函数
(6)
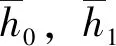
根据构建的轧制变形区横向位移函数,可以分别求出变形区内金属沿轧件宽度方向、厚度方向和轧制方向的应变速度,基于板带轧制三维变形变分法建立轧制变形区耦合运动微分方程
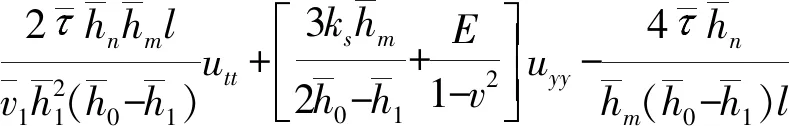
(7)
3 四辊轧机辊系刚柔耦合动力学分析
整理式(4),式(5),式(7)可得板带轧机辊系-轧件多参数耦合动力学模型
(8)
对式(8)采用Galerkin模态离散截断方法来离散,可以分别求解辊系弯曲变形和轧件出口横向位移的模态函数。将模态函数带入上式,可得四辊轧机辊系刚柔耦合动力学控制方程

(9)
式中,

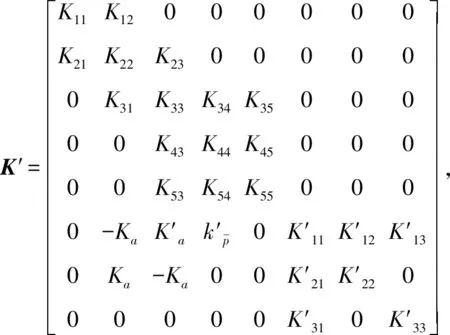
S′=[S1S2S3S4φT1T2T3]T
综合考虑各子模型之间的相互作用规律,建立基于辊系刚柔耦合特性的轧机系统动态仿真模型。轧制变形区耦合动力学模型作为连接轧机各系统运动的桥梁,确定单位轧制压力的横向分布规律,为辊系、板带的变形和主传动系统的运动提供驱动力;同时系统的动力学特性又影响轧制变形区运动规律。模型体系的建立可以仿真分析轧制过程中轧机辊系和变形区内轧件的动力学特性、以及由于外界扰动和参数变化对产品质量的影响,为轧机运行稳定性分析和振动预测提供基础。
以某厂热连轧机组F2轧机发生振动时工作机座的动力学特性为研究对象,对轧机系统动特性进行仿真分析。主要计算参数:入口厚度为0.017 m;出口厚度为0.008 m;板带宽度为1.22 m;工作辊直径为0.793 m;支承辊直径为1.512 m;轧件出口速度为3.6 m/s;密度9.85×103kg/m3;杨氏弹性模量2.1×1011N/m2。图4~图6分别为工作辊沿垂直、水平方向刚性振动的动特性曲线和工作辊扭转振动动特性曲线;图7为轧制变形区金属的横向位移动特性曲线。
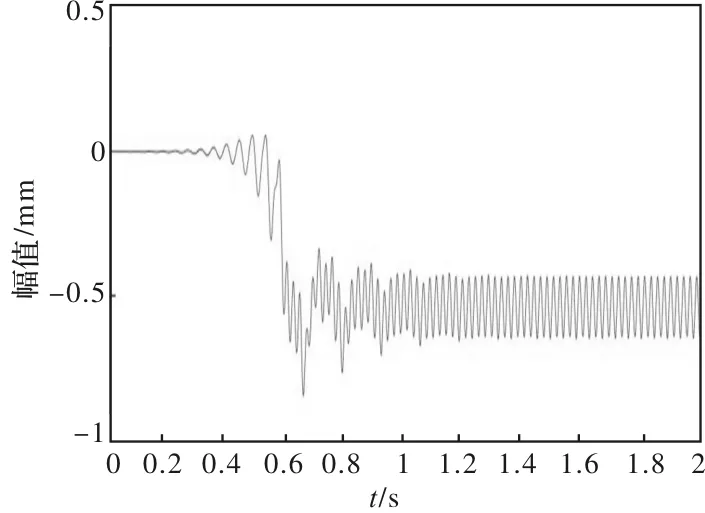
图4 工作辊垂直振动响应曲线
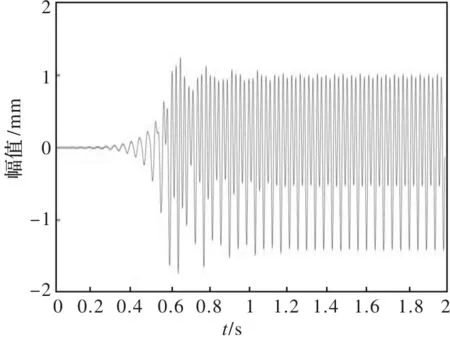
图5 工作辊水平振动响应曲线

图6 工作辊扭转曲振动响应曲线

图7 轧件出口横向位移动特性曲线
4 结论
(1)充分考虑轧制过程中轧机系统刚性振动对轧辊弯曲变形动特性的影响,通过运动学分析,实现柔性多体机械系统中刚体和可变形体的位移场描述,基于弹性梁变形理论和Hamilton变分原理,建立了综合考虑轧辊刚性振动和弯曲变形运动的板带轧机轧辊刚柔耦合动力学模型。
(2)根据动态轧制过程的特点,构造了满足位移边界条件的轧件变形区横向位移函数,利用最小能量原理建立了轧制变形区耦合动力学模型。
(3)仿真结果表明,轧机系统多变量耦合动力学模型能够计算各时刻的轧辊刚性运动和弯曲变形的动态响应特性,即可得到反映板形板厚特性的综合动态信息。
