S304/Q235矫直过程中界面结合能的计算分析

桂海峰，王亚东，李 海，张康康，邢 彤

(1.江苏沙钢集团有限公司 总工程师办公室，江苏 张家港 215600；2.太原科技大学重型机械教育部工程研究中心，山西 太原 030024；3.太原科技大学 材料学院，山西 太原 030024；4.山西柴油机工业有限责任公司，山西 大同 037036)

0 前言

双金属复合板不仅已广泛应用于机械电子、化工、医药等传统行业，还在航天航空、深海钻井、海上填岛、汽车高铁等高新技术领域中有着重要应用[1]。相比较于单一金属材料，双金属复合板具有两种金属材料的优异复合性能和较低的生产成本等优势[2,3]。但在双金属复合板的制备过程中，由于外部环境因素和双金属复合板结合层的材料性能差异，双金属复合板容易产生板形缺陷，如波浪、瓢曲、镰刀弯等[4]。而这些板形缺陷对双金属复合板在之后的加工应用中存在着重要影响[5]。因此，矫直成为双金属复合板加工成型后必不可少的工艺过程。

相对于单一金属板材，双金属复合板在矫直过程中，其结合层开裂问题对其后续的使用性能有着不可忽略地影响。太原理工大学黄庆学[6]课题组通过梁弯曲公式，分析中厚板浪形在辊式矫直过程中的变形行为和矫直效果，得出中性层偏移是改善浪型的重要原因。北京科技大学张清东[7]课题组通过建立和求解带钢翘曲变形力学模型，推导获得带钢翘曲度大小和不均匀纵向延伸的关系。运用屈曲理论对拉伸弯曲的矫直过程展开了研究。太原科技大学王效岗[8]课题组根据双金属板材的弯曲变形特性提出了一种分层算法，在不同金属变形层上运用不同的计算应变方法。北京科技大学臧勇[9]课题组在弹塑性力学基础上，对双金属复合板在平面应力状态下的拉伸回弹呈现出纯弯曲状态，随着载荷的增大残余曲率也随之增大。Changkyu Jung[10]通过实验研究提出了一种针对中厚板冷矫直的残余应力预测模型。Dinh Cuong Tran[11]提出存在于板材中的压缩残余应力可能会存在于后续制造过程中，分析了残余应力和产生的屈曲浪形之间的相互作用。Sami Abdelkhalek[12]建立了一个基于渐进数值方法的张力和残余应力的后屈曲模型，深入研究了残余应力的产生机理和与潜在浪形缺陷之间的关系。

为了更好地研究矫直过程中复合板的界面结合等问题，本文通过对不锈钢S304/普碳钢Q235复合材料进行第一性原理分析，建立相关的界面模型并对其进行优化，计算出不锈钢S304/普碳钢Q235在不同应变下的界面结合能，对材料在矫直过程中进行预测；通过对双金属复合板进行十一辊矫直模拟，分析出复合板在矫直过程中界面结合能的能量变化，验证界面结合能理论的正确性，提高矫直精度，为建立合理的矫直模型提供参考数据。

1 微观建模

在Materials Studios模拟软件中，以Fe40超晶胞模型建立不锈钢S304和普碳钢Q235的微观模型，并进行结构优化，如图1所示。由于不锈钢S304和普碳钢Q235为混合物，不锈钢S304中Fe含量为65.845%，Cr含量为20%，Ni含量为11%，其余元素相对比较少，所以在晶格模型中以Fe、Cr、Ni为基本元素，其比例为7∶2∶1；普碳钢Q235中Fe的含量占96%以上，所以在模型中以Fe为基本元素表示。

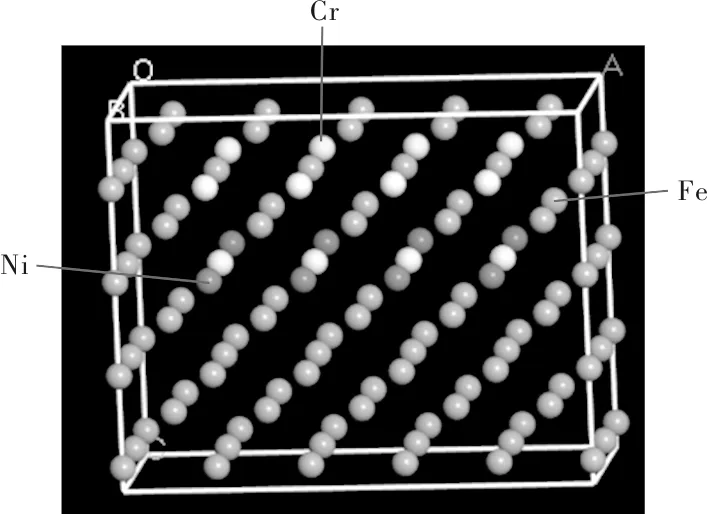
图1 S304/Q235复合板微观模型

通过Materials Studios软件中的Castep模块，利用密度泛函理论DFT(Destiny Functional Theory)计算材料的材料结构和电子性质。基于模拟得到的晶格参数a=1.433 2 nm，b=0.573 78 nm，c=1.146 56 nm，α=β=γ=90°，设定在广义梯度近似GGA框架下，用PBE泛函形式确定交换相关能，求解Kohn-Sham方程。Ensemble系综采取NVT即正则系综,最大迭代次数为500次。采用超软赝势描述价电子与离子实之间相互作用，倒易空间中平面波计算的最大截止能量为380.0 eV，计算收敛精度 1.0×10-6eV/atom。

结合能是一种表示材料稳定性的参数，在微观理论中，它是表示原子在结合成固态物质是需要的能量，基于这种理论，可以认为当固态物体在发生断裂破损时，其微观组织所需要的能量数值是一致。在模拟结果中，结合能的绝对值越大表示其晶体结果越稳定，热力学性能越好；当数值为负时，说明材料越稳定。

复合材料之间界面结合能的计算公式为

(1)

所以其单位结合面积能为

(2)

式中，S为计算S304和Q235所组建界面面积。

2 有限元模拟

利用Abaqus有限元软件建立双金属复合板热矫直过程模型，如图2所示。矫直温度选取450 ℃。

图2 11辊矫直模型示意图

选取全液压十一辊矫直机为原型，建立矫直机中的矫直辊的Abaqus模型。该矫直机采用全液压压下系统，可以精准调节矫直辊的压弯量。矫直机的基本参数如表1所示，压弯量的具体数值如表2所示。

表1 矫直机基本参数

表2 上排矫直辊压下量

选择双金属复合板做为本矫直模拟板材，基层材料选用普通钢Q235，覆层材料选用不锈钢S304。复合板长度为l=900 mm，宽度为b=50 mm，总厚度为h=6 mm。复合板的基本参数参见表3。

建立不同厚度比的复合材料，覆层基层比分别为1∶1进行分析研究。材料模型设置为各向同性弹塑性材料，加工硬化模量取经验值0.01E。

表3 复合板材料基本参数

因为在单次矫直过程中复合板对矫直辊的反作用力较小，所以将矫直辊定义成解析刚体。在实际矫直机工作时，矫直辊是沿中心线进行圆周运动，所以在模型中给矫直辊施加全方位的位移约束和X、Y的转向约束；同时，为了防止复合板在矫直过程中发生左右移动的情况，对复合板的侧面施加了X方向的零位移约束。因为设置矫直辊为刚性材料，在Abaqus中不需要对其进行网格分化，所以只对复合板材料进行网格划分。划分格式为C3D8R：八结点线性六面体单元, 减缩积分, 沙漏控制，复合板的每个单元为5 mm×5 mm×0.5 mm，共19 200个单元。

3 结果与讨论

3.1 第一性原理计算

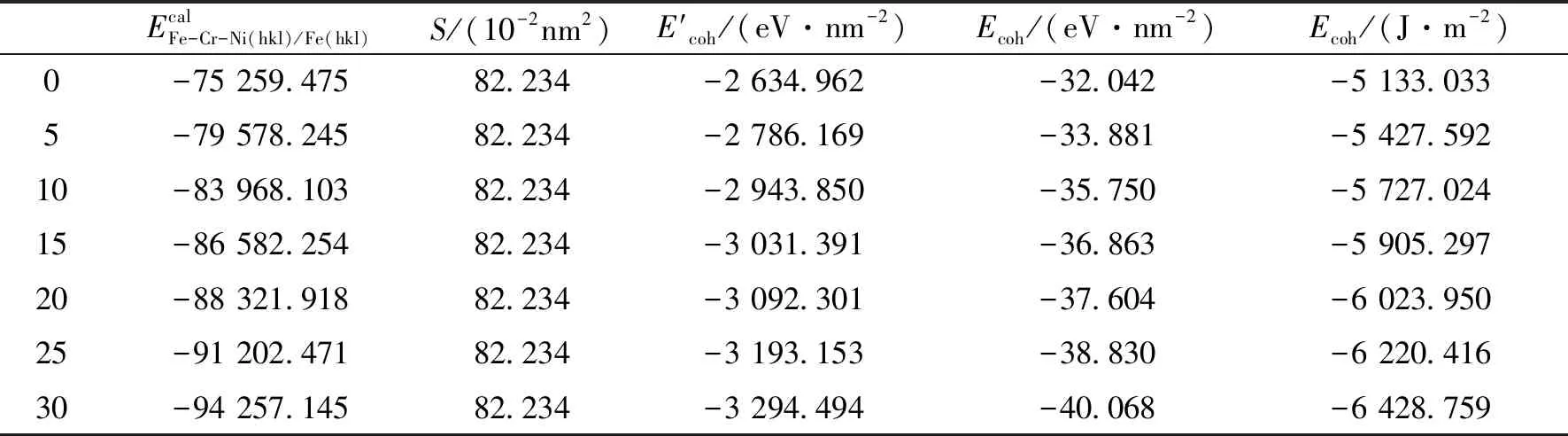
表4 S304/Q235单位面积上界面结合能

根据表4的单位结合能，做出材料模型单位界面结合能随着材料应变量的变化曲线，如图3所示。

模型拟合出应力应变曲线方程为

y=-1E-5x6+0.0008x5-0.0044x4-0.3829x3+

5.353x2+41.799x+5133

R2=1

(3)

图3 单位界面结合能与应变之间的关系

从图3可以看出在0～30%的应变区间内，材料模型中结合能的绝对值随着应变的增大而增大，这表示破坏晶体结构的能量也随之变大；且在应变区间内单位结合能的数值为负，说明材料比较稳定。

3.2 有限元模拟计算

对一受力的结构体来说，应变能是力与位移曲线下所围出来的面积，如图4a所示；单一材料点的应力应变曲线，所包络的面积则是应变能密度，如图4b所示所示。两者之间关系为

(4)

式中，U为应变能;u为应变能密度;V为体积。

图4 应变能与应变能示意图

将板材几何中心层两边各一个单位近似看成复合板的结合层，如图5所示。选取板材中间部位作为参考点，提取应变能密度随时间的变化图，如图6所示。

图5 结合层示意图

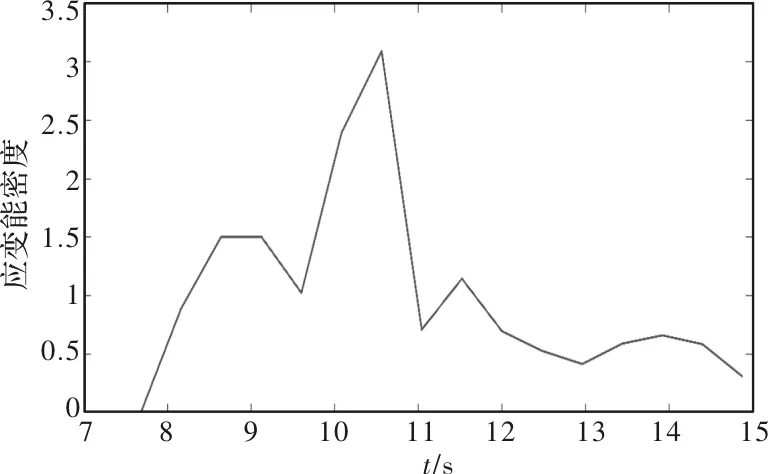
图6 应变能密度随时间的变化图

由模型可知，参考位置在从7.68 s开始矫直辊，至到14.88 s后弯曲离开矫直辊。其中在10.56 s时出现最大值为3.093 555，此时参考位置与第四辊接触，受到的矫直力最大。

已知一个单元网格为0.5 mm×0 mm× 20 mm，选取10.56 s时结合层，共变形10.2%，此刻，弹性变形能为0.215 47 mJ，塑形应变能0.924 57 mJ，共计为1.139 04 mJ，与第一性原理计算出材料的结合能相比较，其结果小于微观模拟，说明在矫直过程，最大矫直力产生的能量不足于使材料发生断裂等现象。

4 结束语

通过对不锈钢S304/普碳钢Q235复合材料采用第一性原理方法进行结构优化，计算界面结合能，拟合单位界面结合能与应变之间的关系图；通过有限元模拟计算不锈钢S304/普碳钢Q235在矫直过程中应变能密度变化，分析结合层应变能密度变化趋势。对比模拟结果，探究界面结合能之间的关系，验证界面结合能理论的正确性，提高矫直精度，为建立合理的矫直模型提供参考数据。