基于改进蚁群算法的植保无人机路径规划方法

王 宇 王文浩 徐 凡 王泾涵 陈海涛

(东北农业大学工程学院， 哈尔滨 150030)

0 引言

植保无人机近年来发展迅速，相比于有人驾驶飞机，植保无人机飞行高度较低、药液飘移较少、具有更强的地形适应能力，并且遥控作业保证了操作人员的安全，其在小面积农田或作物多样化的种植区已经体现出显著优势。日、韩等国已经普遍采用无人机进行植保作业。我国既有集中的大块农田，也有数量众多较为分散的或地形特殊的小块农田，发展植保无人机具有广阔的市场需求[1-5]。目前，部分植保无人机产品已具有对简单多边形作业区域进行路径规划的功能，但实际作业环境有时较为复杂，如多个具有高低起伏的作业区域。面对较为复杂的作业环境，如何规划出更加合理的作业路径，以进一步提高植保无人机的作业效率，成为亟待解决的问题。

植保无人机的作业路径采用往复回转式路径，并要求对作业区域实现全覆盖[6-8]。文献[9]基于扫描线方法提出了一种无人机全覆盖路径规划方法，该方法将复杂多边形区域合理划分，可进一步提高无人机作业效率。文献[10-11]基于改进的遗传算法提出了一种植保无人机全局航线规划算法，实现了多块农田的路径规划。文献[12]基于改进的退火算法提出了一种适用于内含障碍物农田的植保无人机路径规划方法，可实现航向角的优化。上述研究中均未考虑三维地形的影响，植保无人机作业时仿地形飞行，以保证无人机与作物保持一定距离，若路径规划时不考虑三维地形的影响，则会使规划结果与实际距离不一致，导致诸多计算结果失去对实际作业路径的指导意义[13]。文献[14]基于Morse分解方法提出了一种多架次无人机全覆盖路径规划方法，能够在内含障碍物的三维作业区域中进行路径规划。文献[15-16]提出了基于引力搜索算法的路径规划方法，该方法能够针对具有不规则边界的三维地区进行路径规划。但研究中未对作业路径的航向角进行规划，且作业路径的排序采用贪婪算法，导致计算结果避开较优解的概率增大。

针对上述问题，本文提出一种适用于多个具有复杂多边形边界与内部障碍物的三维作业区域的植保无人机路径规划方法。在扫描生成水平面内的作业路径基础上，经过离散化与插值等处理，获得三维作业路径；对蚁群算法(Ant colony optimization, ACO)进行适用性改进，以实现对三维作业路径的排序优化。

1 基于改进蚁群算法的路径规划方法

基于改进蚁群算法的路径规划方法主体包含作业路径生成算法与改进的蚁群算法，两种算法各自的输入输出如表1所示。

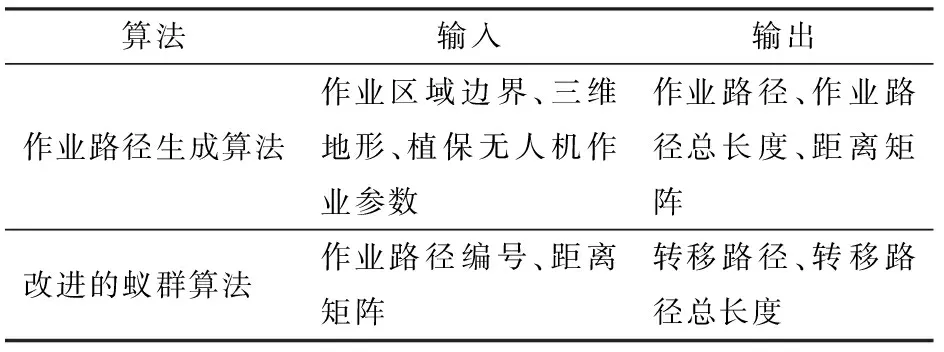
表1 两种算法的输入与输出Tab.1 Input and output of each algorithm

表1中，作业路径是指进行喷施作业的路径；距离矩阵是指作业路径端点之间的距离组成的矩阵；转移路径是指在作业路径端点之间移动的非喷施作业路径。算法针对多个作业区域进行路径规划的基本流程如图1所示，图中Pk与Dk分别为作业区域k(k=1,2,…,n)内的路径集与距离矩阵。

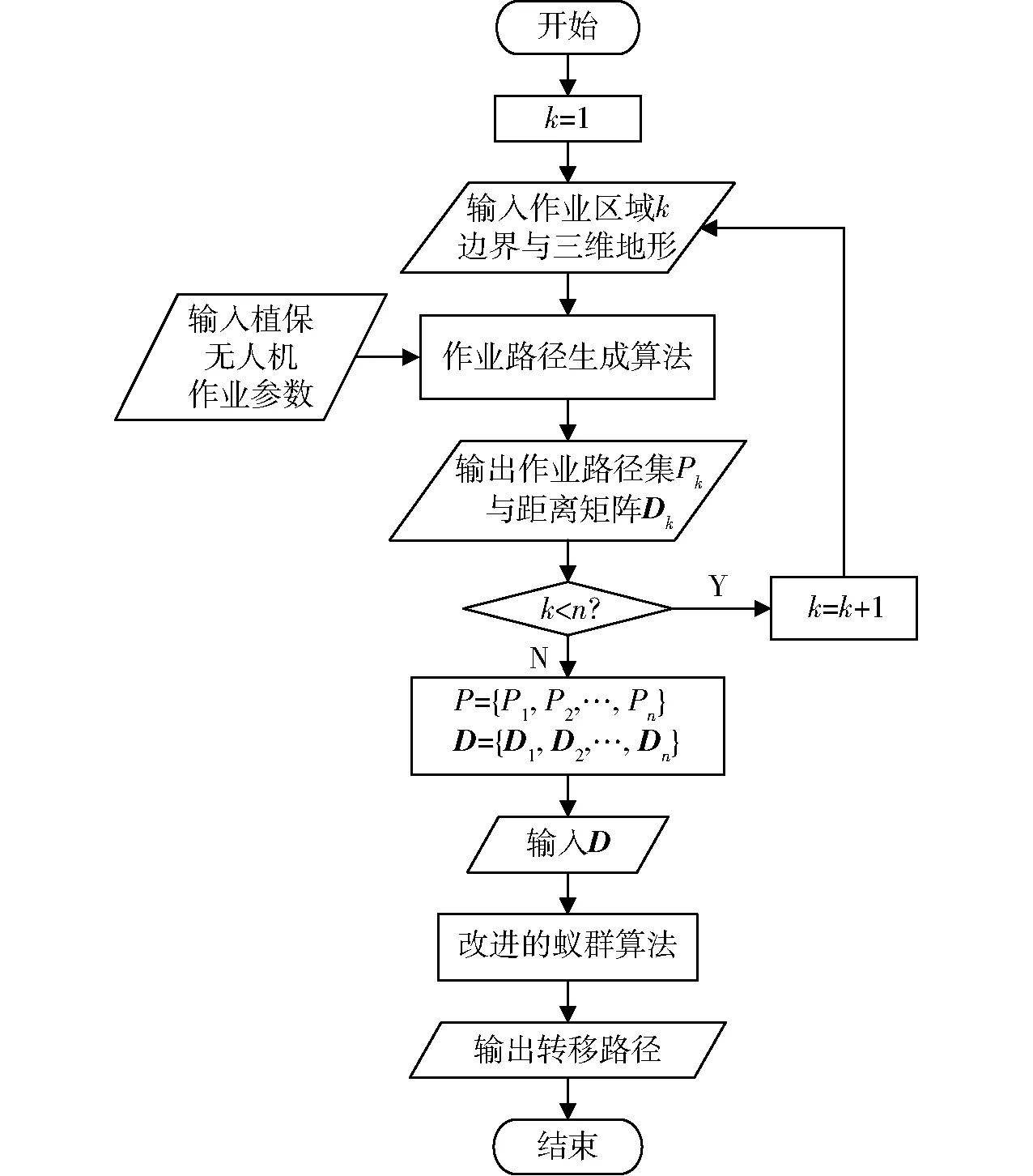
图1 基于改进蚁群算法的路径规划方法流程图Fig.1 Flowchart of path planning approach based on ACO

2 作业路径生成算法

作业路径生成算法的基本思路：①根据作业区域边界生成具有一定方向的水平面内的作业路径。②根据三维地形，将水平面内的作业路径转变为三维作业路径。

2.1 水平面内的作业路径生成方法

设植保无人机作业路径与坐标系X轴正向的夹角为航向角θ、作业幅宽为w。水平面内的作业路径生成方法的步骤为：①输入作业区域边界顶点坐标。②以-θ为转角旋转作业区域边界。③以w为间距建立一组与坐标系X轴平行的、能够覆盖作业区域的扫描线。④求第i条扫描线与边界的交点集。⑤以x坐标值递增将交点集排序。⑥从前至后依次将交点集内的交点两两配对，每对交点之间的连线即作业路径，执行完该步后i=i+1。⑦重复步骤④直至求出所有扫描线与边界形成的作业路径。

针对图2所示的内部包含障碍物的凹多边形作业区域进行具体执行过程说明，蓝色直线为扫描线中的一条，分别与作业区域边界交于A1～A4点，按照x坐标值递增排序后，依次两两配对并连线后得到线段A1A2、A3A4，即作业路径。

图2 扫描线与边界的交点Fig.2 Intersections of scan lines and boundary

在执行步骤④至⑥时，可能会出现如图2所示的红色扫描线与边界的顶点相交的特殊情况。在交点A5处，扫描线分别与2条边界的顶点相交，可视为2个交点重叠。同理，图2中除点A11以外的所有交点，均为相互重叠的2个交点。处理这种情况时，若将重叠的2个交点合并成1个交点，再前后依次两两配对后，则会得到线段A5A6、A7A8、A9A10、A11A12，其中，线段A5A6、A9A10均位于作业区域外，而正确的作业路径A6A7、A8A9却未计入作业路径，这显然不合理。

针对上述情况，认为扫描线与边界的交点总是在扫描线的一侧，求出交点集后，再剔除交点集中重叠的交点。此处设交点总是在扫描线的上侧，对图2中红色扫描线与边界的交点进行处理：交点A5与边界K1、K2均在扫描线上侧，所以交点A5在边界K1、K2上，此处是2个重叠的交点；交点A6与边界K3在扫描线上侧，边界K4在扫描线下侧，所以交点A6在边界K3上，认为此处只有1个交点；点A7在边界线上侧，边界K5、K6在扫面线下侧，认为此处没有交点；其他交点处理方式类似于这3种情况。将重叠的交点从经过处理的交点集中剔除，剩余交点A6、A9、A11、A12，按步骤⑥可得作业路径A6A9、A11A12，包括且仅包括所有的位于作业区域内的作业路径。另外，认为重合的线彼此之间没有交点。

2.2 三维作业路径生成方法

如图3所示，对于同一块正方形的作业区域，若不考虑三维地形，则作业路径无论沿着方向1还是方向2进行规划，其总距离应该是相同的；但考虑三维地形时，显然沿着方向1规划，作业路径总长度更短。所以，进行作业路径规划时，有必要考虑三维地形的影响。

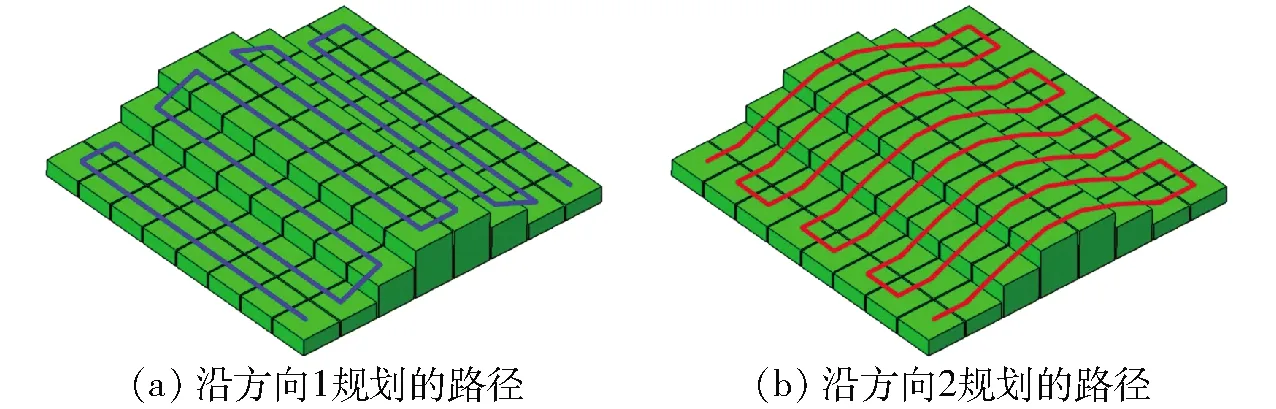
图3 正方形作业区域三维作业路径Fig.3 3D path in square farmland

三维作业路径生成步骤为：①以一定的间距a建立一组与水平面内的作业路径垂直的、能够覆盖作业区域的直线。②求取直线与水平面内的作业路径的交点，从而将作业路径离散成被交点分隔的线段。③运用交点与作业路径端点坐标在已知三维地形曲面上插值得各点相应的高度。④连接同属一条作业路径上的各点即得三维作业路径。⑤以θ为转角旋转三维作业路径。

其中，离散直线间距a越小，精度越高、计算量越大，若地形起伏较平缓，a可取较大值；若地形变化较剧烈，则a须取较小值。

通过上述方法，能够实现在一定航向角θ条件下的三维作业路径总长度与数量的计算，作业路径生成算法以航向角θ为变量，0≤θ<π，由于变量少，变化范围小，所以采取以π/180为步长遍历的方式对θ进行寻优，优化目标为作业路径总长度尽量短、路径之间转移次数尽量少，由于每条作业路径只经过一次，所以作业路径之间的转移次数可视为作业路径数量，目标函数E为

(1)

其中

式中ωN——作业路径之间转移次数权重

N——作业路径数量

Nmax、Nmin——作业路径数量最大值、最小值

ωL——作业路径长度权重

Lmax、Lmin——作业路径总长度最大值、最小值

L——作业路径总长度

Li——第i条作业路径的长度

3 改进的蚁群算法

得出三维作业路径之后，还须按照一定顺序将其进行连接。对于如图3所示的简单多边形作业区域，将作业路径顺次连接即可。但是对于较为复杂的情况，例如图4所示的4个作业区域，对其内的作业路径进行排序时须按照一定的策略，才能使转移路径总长度较短。

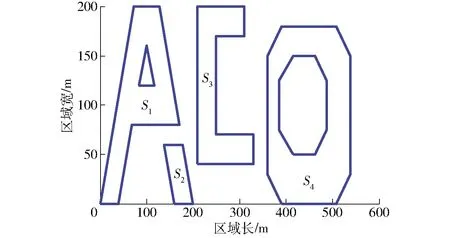
图4 算例作业区域Fig.4 Example farmland

作业路径的排序问题，类似于旅行商问题，将作业路径视为节点，对于所有的节点，既要求遍历，又不能重复。在此前提下求节点的排序，以使节点之间的转移路径总长度最短，若采用遍历方式求该类问题的最优解，遍历次数为节点数量的阶乘，随着节点增多，计算量增大[17-18]。

作业路径的排序问题更为复杂，旅行商问题中2个节点之间的距离固定，而作业路径排序问题中每条作业路径均具有2个端点，植保无人机须从其中一端点进入，从另一端点离开，使得任意2条作业路径之间的距离具有4种可能。

蚁群算法是一种启发式智能优化算法，适用于处理旅行商问题，能够以转移路径最短为目标，得出较优的节点排序。其基本思路为：蚁群分批次出发，每只蚂蚁选择一条遍历各节点的路线，并在路线上留下信息素，总长度较短的路线上信息素较多，下一批次蚂蚁选择路线时，会受到信息素的引导，随着批次增多，总长度较短的路线上信息素不断积累，最终，蚁群会集中到信息素最多的路线上[19-22]。

为了解决作业路径排序问题，本文将蚁群算法改进，使其对作业路径排序的同时，考虑每条作业路径的进入点，建立的优化模型如下：

(1)作业路径与进入点排序

将每条作业路径顺次编号i(i=1,2,…,N)，第i条作业路径的2个端点分别为Ai与Bi，每只蚂蚁选择一条遍历所有作业路径的路线，其中，第m只蚂蚁选择的路线为

(2)

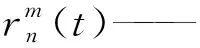
t——当前蚂蚁批次

由于每条作业路径均有2个端点，蚂蚁选择不同的端点进入时，转移路径的长度不同，所以还须为蚁群算法附加记录每条作业路径的进入点的功能

(3)

式(2)、(3)中，当n=1时，是蚂蚁的起点，处理方式有两种：①人为选定起点，对应人为选定植保无人机作业起点的情况。②算法随机选择一条作业路径与其上一端点作为起点，此时植保无人机的作业起点由算法优化得出。

对于确定起点之后作业路径与相应进入点的选择，须按照一定的概率依次进行。设第m只蚂蚁现位于作业路径i上，选择作业路径j，此时分为两种情况，分别为选择端点Aj与端点Bj作为进入点，选择两端点的概率各为

(4)

(5)

式中α——信息素对选择概率的重要程度

β——启发因子对选择概率的重要程度

τij(k)(t)——作业路径i与作业路径j(k)之间的信息素，初始值为1

ηiAj(k)、ηiBj(k)——从作业路径i到达端点Aj(k)、Bj(k)的启发因子

Vm——当前第m只蚂蚁可选择的作业路径集合

(2)启发因子

启发因子与作业路径之间的距离矩阵有关，距离矩阵计算式为

(6)

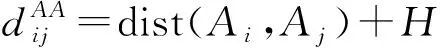
(7)

(8)

dist(Ai,Aj)——端点Ai与Aj的欧氏距离

AiAj——端点Ai与Aj间线段

S——作业区域

h——设定的安全高度

H——升降飞行距离

若线段AiAj不包含于作业区域S，则转移时还须按照设定的安全高度h进行升降，采用如下策略判断线段AiAj是否包含于作业区域S：①判断线段AiAj是否与作业区域S的边界内交，若内交，则不包含于；若只在端点处相交，则由策略②判断。②采用射线法判断相邻两交点的中点是否位于作业区域S内，只要存在不位于作业区域S内的中点，则不包含于；若均位于作业区域S内，则包含于。

同理还可求

(9)

(10)

启发因子计算式为

(11)

(12)

(3)信息素

批次之间信息素的更新策略为

τij(t+1)=(1-ρ)τij(t)+Δτij(t)

(13)

其中

式中ρ——信息素挥发系数

Δτij(t)——第t批次与t+1批次之间的信息素变化量

Q——信息素增加强度系数

lm(t)——第t批次第m只蚂蚁走过的转移路径总长度

4 算例检验

4.1 作业路径生成算法检验

相关参数设置如下：w=5 m，a=10 m，ωN=0.5，ωL=0.5。对如图4所示的4个作业区域生成作业路径，其中区域S1与区域S4内部具有障碍物。图5为4个作业区域所处的三维地形，构成曲面的点阵中，各坐标点在水平面内彼此之间相距10 m。对航向角θ遍历寻优后生成的作业路径如图6所示。

图5 作业区域三维地形Fig.5 3D terrain of farmland

图6 作业路径Fig.6 Spray path

由图6可知，在区域S3与S4中，所得作业路径方向不同，且三维地形使原本为直线的作业路径变为具有高度变化的曲折作业路径，使作业路径变长，具体计算结果如表2所示。

作业区域S1与S2中，三维作业路径与水平面内的作业路径的航向角相同，由于三维作业路径具有高度变化，所以总长度均较长。作业区域S3与S4中，三维作业路径与水平面内的作业路径的航向角差异明显，如作业区域S4中，水平面内的作业路径航向角为92°，基本与三维作业路径航向角垂直。采用作业区域S3水平面内的航向角9°，通过式(1)计算三维作业路径的目标函数E=0.29，大于0.14；同理，计算作业区域S4水平面内的航向角92°对应的三维作业路径的目标函数E=0.14，大于0.12，计算结果直接表明了生成作业路径过程中若不考虑三维地形的影响，会导致航向角优化结果出现偏差。

表2 作业路径计算结果Tab.2 Results related to spray path

4.1.1离散直线的间距a

保持其他参数不变，改变离散直线的间距a，计算结果如表3所示。

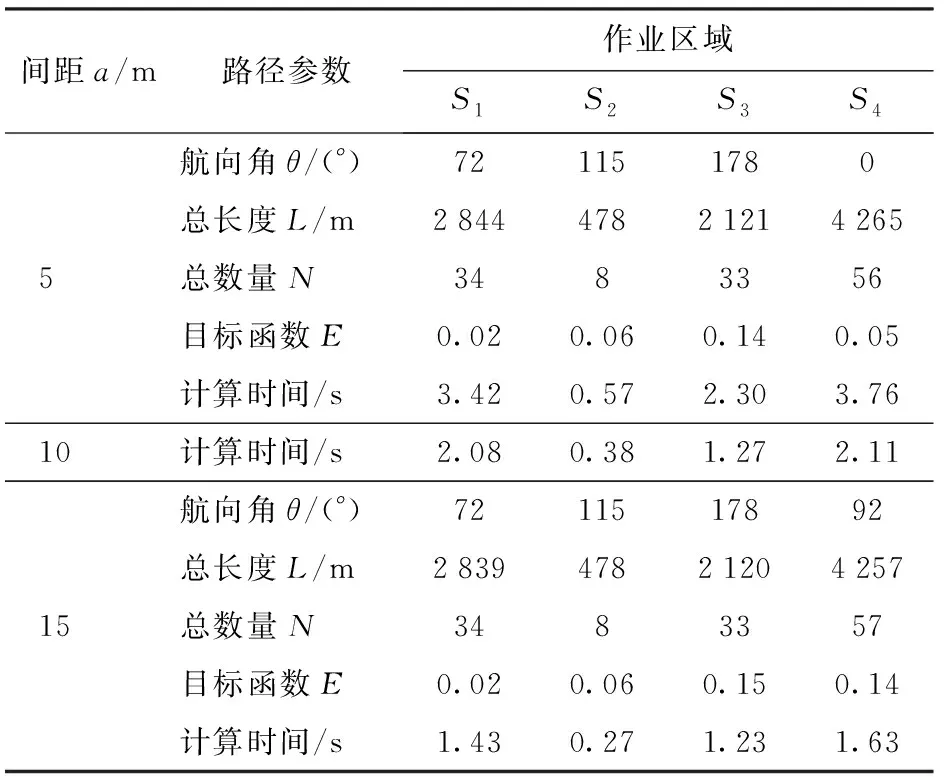
表3 不同间距a的作业路径计算结果Tab.3 Results related to spray path for different values of a

表3中，当间距a=10 m时，相关计算结果见表2中的三维作业路径的计算结果。由表3可知，间距a越小，计算时间越长。这主要是因为间距a缩小后，离散直线与每一条作业路径的交点增多，而每个交点都需要在三维地形曲面上进行插值计算。

在作业区域S1与S3中，间距a越小，作业路径总长度越长，这是由于交点数量增多后会使作业路径更好地与地面仿形。如图7所示，对于一条作业路径，间距a较小时，为蓝色线，间距a较大时，为红色线。显然蓝色线的总长度更长，也更接近地形曲面。以不同的间距a得出的作业路径总长度虽有差距，但相差不大，这主要是因为作业区域内地形的坡度较小，且在优化后的航向上，地形起伏较少。如图6所示，作业区域S1中的每一条作业路径，均近似于与水平面具有一定倾斜角度的线段。而对于一条倾斜的线段，只要两端点的位置确定，则总长度即确定，不管将其分为多少个离散线段进行计算，总长度均不受影响。

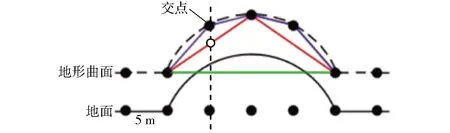
图7 作业路径的生成Fig.7 Generation of spray path

当间距a=15 m时，作业区域S4中，优化所得的航向角为92°，与不考虑三维地形时优化所得的航向角相同，说明此时间距a取值过大，使得三维作业路径上的交点过少，无法通过插值得到足够的地形信息，如图7绿色线所示，由于缺少了中间3个交点，导致路径包含的地形信息缺失。

由于构成三维地形曲面的点阵中各点在水平面内的间距为10 m，当间距a=5 m时，已经超过地形信息的精度，较难使作业路径相关计算结果精度进一步提高，而且还会导致计算时间变长。可假设图7中红色线连接的点为地形曲面点阵中的点，精度为10 m，若采用间距a=5 m在其上进行插值，则会出现空心交点所示的情况，此时，作业路径长度计算结果与间距a=10 m时相同，但却需要对多余的点进行计算。所以，针对该算例，间距a选取10 m较为合适。

因为作业区域S2的地形为平地，使得不同的间距a所得结果相同，此时缩小间距a仅会导致计算时间增加，所以对作业区域S2可不进行离散处理。

4.1.2作业幅宽w

根据大疆T16型植保无人机设置作业幅宽w=6.5 m，其他参数设置保持不变，三维路径相关计算结果见表4。

由表4可知，作业幅宽w增至6.5 m后，各项计算结果均会受到影响。相比于作业幅宽w=5 m时，作业路径的总长度缩短2 440 m，总数量减少30，这主要是因为作业幅宽w增加后，使作业路径之间的间距变大，从而用较少的作业路径便可覆盖作业区域；作业路径数量减少，作业路径总长度也就随之缩短。作业路径的数量的变化也导致了优化后的航向角的变化，例如作业区域S4中，优化后的航向角为90°，与作业幅宽w=5 m时得出的航向角相垂直，这主要是因为沿90°航向角的单条作业路径长度较长，当该方向作业路径数量减少时，作业路径总长度缩短幅度较大。

表4 w=6.5 m时三维作业路径计算结果Tab.4 Results related to 3D spray path with w=6.5 m

4.2 改进的蚁群算法检验

本例对4.1节中当w=5 m时得出的三维作业路径进行排序，改进的蚁群算法的相关参数设置如下：总批次T=100，蚁群规模M=50，α=1，β=5，h=3 m，Q=100，ρ=0.1。根据不同的作业需求，分别对选定与未选定作业起点的情况进行计算。

4.2.1选定作业起点的作业路径排序

选定作业起点为C1(0,0,0)，计算得出作业路径排序，结果如图8a所示，图中蓝色线段为作业路径，红色线段为转移路径，转移路径总长度见表5。

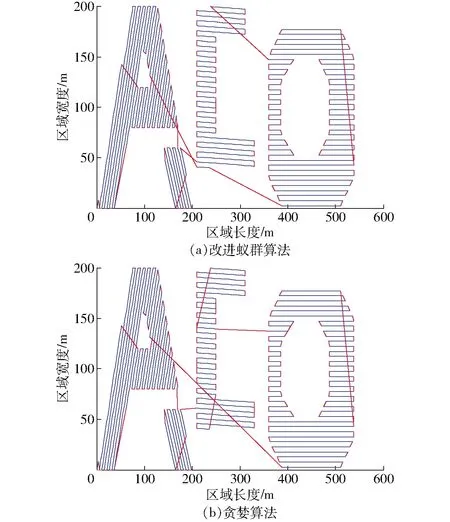
图8 选定作业起点时的作业路径排序Fig.8 Sequence of spray paths with selected starting point

贪婪算法是一种能够快速求解最短路径问题的算法，其基本思路为选择下一条作业路径时，总是选择最近的那一条[23-25]。与贪婪算法的计算结果进行对比，能够一定程度上验证改进的蚁群算法的寻优性能。以C1为起点，采用贪婪算法进行作业路径排序，结果如图8b所示，转移路径总长度见表5。

表5 转移路径总长度Tab.5 Total length of transfer paths m

表5中记录了5个作业起点各自对应的转移路径总长度，其中，C1与C2为作业区域边界的顶点，C3为作业区域外的点，A71与A73为三维作业路径的端点。由表5可知，针对选定的作业起点进行作业路径排序，基于改进的蚁群算法得到的转移路径总长度均较短，比贪婪算法计算结果缩短3%～28%，相差最大值为694 m。

计算过程中发现，采用贪婪算法进行作业路径排序时，转移路径总长度只与作业起点有关，因为贪婪算法总是按照最近原则选择下一条作业路径，当作业起点与待排序的作业路径一定时，转移路径即已经被确定。采用贪婪算法针对每个作业路径端点进行作业路径排序，其中最短与最长的转移路径对应的作业起点分别为A71与A73，转移路径总长度见表5。

而基于改进的蚁群算法针对选定的作业起点进行作业路径排序时，多次求解的结果不唯一。以C1为作业起点，5次运行改进的蚁群算法所得的转移路径总长度分别为1 705、1 797、1 735、1 756、1 745 m。

这些数据显示，生成的转移路径总长度上下浮动，这是因为改进的蚁群算法是一个迭代计算过程，图9表示第1次运行时的迭代计算过程，转移路径总长度随着迭代计算次数增加不断缩短，由于总迭代计算次数较少，转移路径总长度仍有缩短趋势，还未出现信息素具有绝对优势的转移路径，蚂蚁仍会积极搜索可行的转移路径。

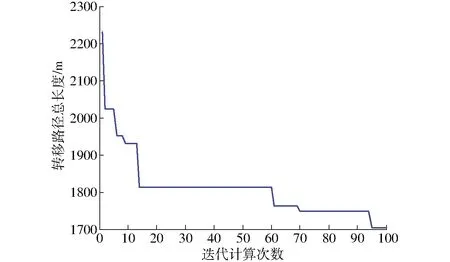
图9 转移路径总长度在100次迭代计算中的变化趋势Fig.9 Trend of total length of transfer paths with 100 iterations

在图9所示第100次迭代计算结果的基础上，再继续进行900次迭代计算，过程如图10所示，优化后的转移路径总长度为1 683 m，当计算至第70次时，优化结果已经小于1 685 m，其后的830次迭代计算降低幅度小于2 m，而在图9所示的前100次迭代计算中，优化解结果降低幅度超过500 m，说明迭代计算趋于收敛。所以应尽量使总的迭代计算次数超过200次，以获得更加优化的结果。

4.2.2未选定作业起点的作业路径排序

该种情况下作业起点与转移路径由算法一并计算得出。基于改进的蚁群算法得到的转移路径如图11a所示，红色线段与绿色线段均为转移路径，其中绿色线段连接本次作业的起点与终点，计算得到的作业起点为A92(360 m, 67.5 m, 1.5 m)，转移路径总长度为1 661 m，比贪婪算法计算得出的最短转移路径短102 m。以A92作为作业起点，采用贪婪算法计算得出的转移路径如图11b所示，转移路径总长度为2 383 m，比基于改进的蚁群算法所得的结果长722 m。

图11 未选定作业起点时的作业路径排序Fig.11 Sequence of spray paths without selected starting point

在选定与未选定作业起点的条件下，通过对改进的蚁群算法与贪婪算法所得的转移路径进行对比可知，相同作业起点时，总是改进的蚁群算法所得的转移路径总长度更短，因为改进的蚁群算法中，通过启发因子，体现了每一次转移时的距离对作业路径选择的客观影响，同时，还通过信息素，保证了转移路径总长度的全局主导地位。

5 实例检验

选取东北农业大学试验田进行实际地形的路径规划，作业区域共5块，如图12所示，其中作业区域S4内部圆形为一高3 m的凸台，其上也须作业，其余作业区域均为平地，已知的地理信息中构成三维地形曲面的点阵水平面内的间隔为20 m，根据算例相关结论，设置作业区域S4离散直线的间距a=20 m，对其余作业区域不进行离散处理。作业区域之外存在道路、树木、棚屋，相比于作业区域最低处分别高0.5、15、2.5 m，安全高度须大于其中的最大值，因此设置h=18 m。植保无人机作业幅宽w=5 m，总批次T=200，其余参数与算例设置一致。

图12 实际地形作业区域Fig.12 Actual farmland

采集作业区域顶点坐标建立数字化作业区域边界，顶点坐标如表6所示。作业区域S4中的圆形凸台区域的圆心坐标为(426 m,-128 m)，半径为35 m。

进行三维作业路径生成，得到各作业区域内的作业路径与航向角，如表7所示。

当选定C1(0, 0, 0)为作业起点时，作业路径排序结果如图13所示，转移路径总长度见表8。

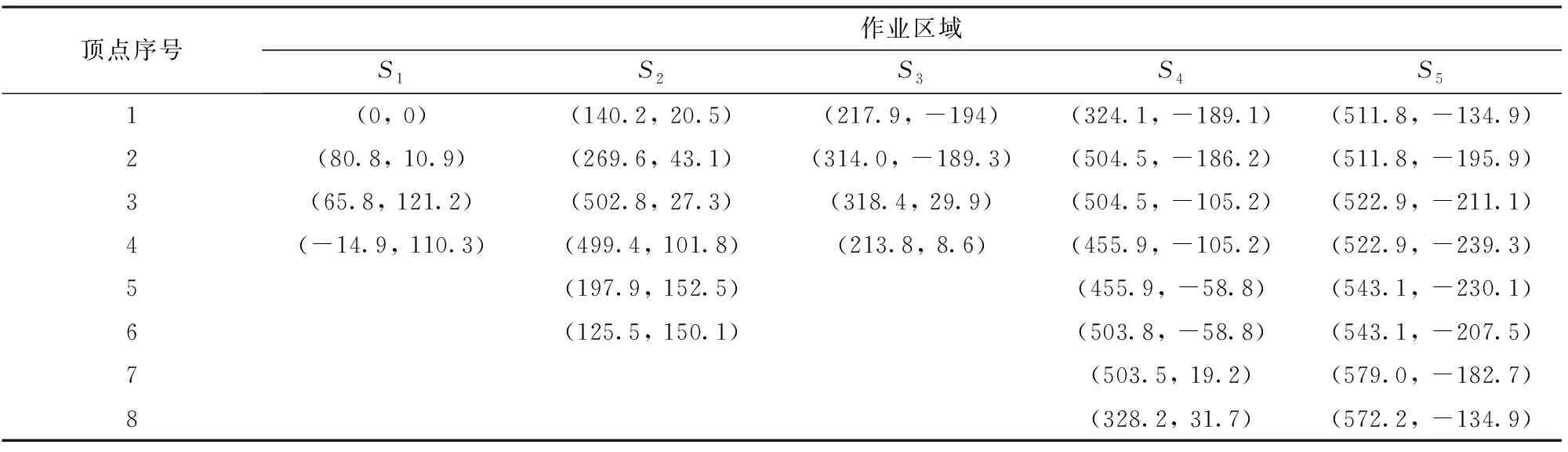
表6 作业区域顶点坐标Tab.6 Coordinates of spray area boundary vertices m

表7 实际地形作业路径计算结果Tab.7 Results related to spray path in actual farmland

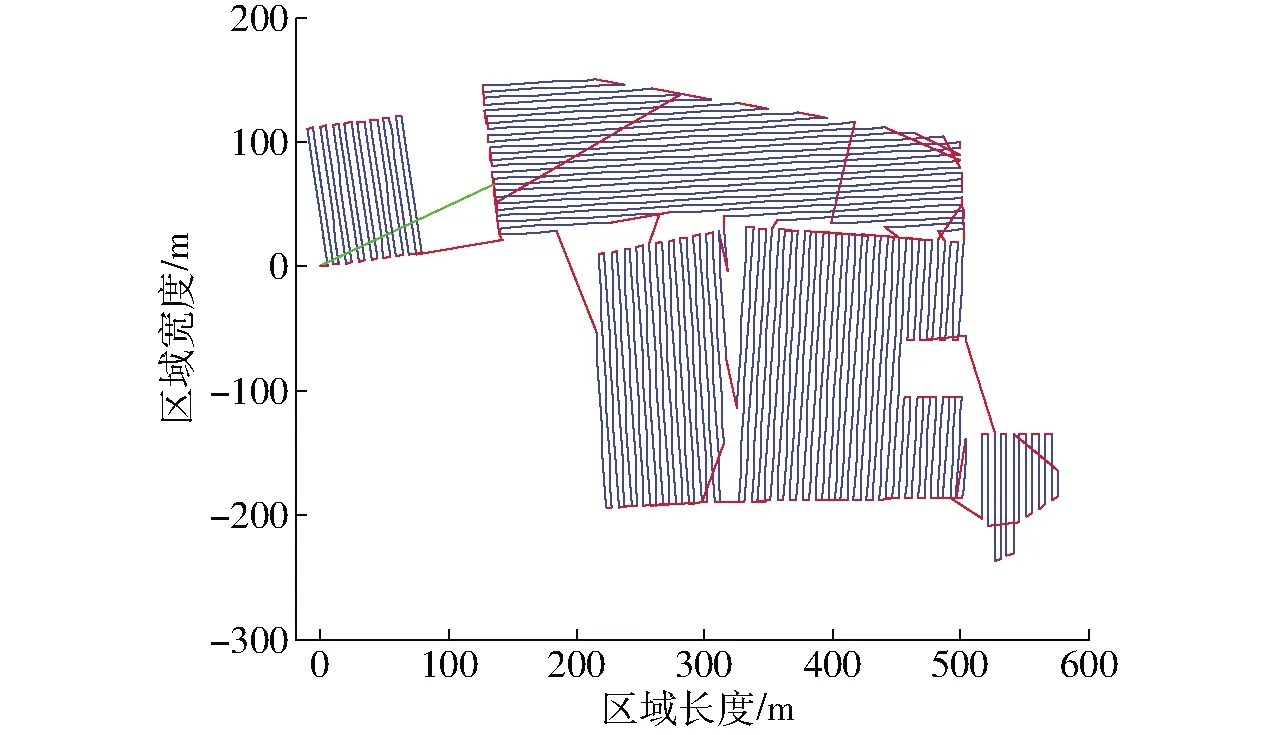
图13 实际地形作业路径排序Fig.13 Sequence of spray paths in actual farmland

表8 实际地形转移路径总长度Tab.8 Total length of transfer paths in actual farmland m

表8中，记录了3个不同的作业起点各自对应的转移路径总长度，C1为作业区域边界的顶点，A75与B58均为作业路径的端点，A75为改进的蚁群算法所得最短转移路径对应的起点，B58为贪婪算法所得最短转移路径对应的起点。表8中数据显示，相同作业起点时，改进的蚁群算法所得的转移路径均较短，相比贪婪算法所得转移路径缩短7%～13%，相差最大值为600 m；改进的蚁群算法所得最小值为4 001 m，比贪婪算法所得最小值(4 368 m)缩短367 m，数据均表明改进的蚁群算法可规划出较为高效的路径。

6 结论

(1)提出了基于改进蚁群算法的植保无人机路径规划方法。该方法将扫描生成的水平面内的作业路径离散化，通过在三维地形曲面上插值求取三维作业路径，使航向优化过程能够考虑三维地形影响；对蚁群算法进行改进，使其具有同时记录作业路径与相应进入点的机制，从而能够对作业路径合理排序。

(2)在算例检验中，针对同一作业区域，规划出的作业路径航向角相差最大值为92°，这说明路径规划过程中考虑三维地形的必要性。算例中，针对一系列相同的作业起点，改进蚁群算法所得的转移路径总长度比贪婪算法所得结果缩短3%～28%；在未选定作业起点情况下，改进蚁群算法与贪婪算法求得的转移路径总长度最小值分别为1 661 m与1 763 m。实例检验中，在相同作业起点情况下，改进蚁群算法所得的转移路径总长度比贪婪算法所得结果缩短7%～13%；在未选定作业起点情况下，改进蚁群算法与贪婪算法求得的转移路径总长度最小值分别为4 001 m与4 368 m。说明改进蚁群算法具有良好的寻优能力。另外，算例与实例中的作业区域具有复杂多边形边界、三维地形、内含障碍物等特征，表明本文提出的路径规划方法具有一定实用性。

(3)提出的路径规划方法尚未考虑作业过程中的农药补充与电池更换。进行农药补充与电池更换时，植保无人机须由当前位置中断，再返航至补给点，返航路径必然会影响路径的总长度，因此本文提出的路径规划方法更适用于较小面积的作业区域。