融合GA与SVR算法的小麦条锈病特征优选与模型构建
2020-11-24白宗璠黄文江
竞 霞 张 腾 白宗璠 黄文江
(1.西安科技大学测绘科学与技术学院, 西安 710054; 2.中国科学院空天信息创新研究院, 北京 100094)
0 引言
小麦条锈病是小麦的主要病害之一,具有爆发性和流行性的特点,严重影响小麦的安全生产[1]。实时准确获取小麦条锈病发病信息,对小麦病害的精准防治、减少农药污染、提高小麦产量和质量具有重要意义。人工田间取样的传统病害调查方式费时、费力、时效性差,难以满足多点同时大范围监测的需求[2]。遥感技术具有快速、大面积、无损害等优点,已被广泛应用于小麦病害监测中[3-5]。高光谱遥感数据能提供精细的地物光谱信息,定量识别作物受病虫害的胁迫程度,受到了众多学者的关注[6-9]。目前,小麦病害高光谱遥感监测主要利用光谱特征参量与病情指数之间的相关性作为优选敏感因子的标准,采用过滤法确定模型构建的特征参量[10-12],该方法从数据特征的结构出发,特征参量的选择独立于模型算法,算法简单、通用性好[13],但忽略了各特征参量间的相关性,难以保证所选特征参量是适合于建模算法的最优因子,影响了模型构建的精度。封装法将特征选择算法和建模方法相结合,进行特征参量提取,能够降低模型的复杂性,提高模型预测精度[14-16]。已有研究表明采用封装法进行特征选择和模型构建能够有效剔除光谱冗余信息[17],以较少的敏感波段达到较高的反演精度[18],所建模型具有较强的预测能力[19]。在众多的特征选择和模型构建算法中,GA能够模拟自然选择和遗传学机理的生物进化过程,具有原理和操作简单、通用性强、能在短时间内达到全局最优的特点[20],在特征选择中得到了广泛应用[21-23]。而SVR算法具有适应性好、泛化能力强等特点,更适合小样本数据[24]。
小麦受条锈病菌侵染后,其水分及叶绿素含量、光合速率和光能转换率等生理生化指标均会发生变化[25]。反射率光谱数据能够反映植被生化组分信息,但对作物光合活性不敏感,难以揭示植被光合生理状态[26],且受阴影等非绿色景观成分的背景噪声影响较大[27]。自然光照条件下的叶绿素荧光受背景噪声的影响较小[28],能够直接探测到植被的光合作用状态[29],遥感探测作物胁迫的精度较高。冠层SIF和反射率光谱在作物病害的遥感探测中各有优势和局限性,已有研究表明,在反射率光谱数据中融合冠层SIF能够提高小麦条锈病病情的估测精度[30-32]。基于此,本文将反射率吸收参数与冠层SIF数据作为初始特征集合,以SVR模型交叉验证精度作为评价标准,利用封装法将GA和SVR算法相融合,对特征子集与SVR参数进行联合优选,建立基于遗传算法优选特征参量的小麦条锈病严重度估测的GA-SVR模型,并将其与CC分析法提取特征参量所建模型的精度进行对比,探讨GA-SVR模型在小麦条锈病遥感监测中的适用性,确定遥感监测小麦条锈病的敏感因子及模型。
1 材料和方法
1.1 试验概况
试验区位于河北省廊坊市中国农业科学院试验站(39°30′40″N,116°36′20″E),小麦试验品种为对条锈病比较敏感的铭贤169号,2018年4月9日(小麦起身期)采用浓度为0.09 mg/mL的孢子溶液利用喷雾法对小麦进行条锈病接种。试验区小麦平均种植密度为113株/m2,分为健康组(编号为 A、D)和染病组(编号为B、C),健康组与染病组之间设置5 m隔离带,并对健康组采用打药处理防止病害发生。每个试验组的面积为220 m2,每个组分为8个样方(A1~A8、B1~B8、C1~C8、 D1~D8),即健康组和染病组各16个样方。
1.2 数据获取
1.2.1冠层光谱测量
试验分别于2018年5月18日、5月24日和5月30日3个时期测量小麦条锈病不同病情下的冠层光谱数据,测量仪器为美国ASD公司生产的ASD Field Spec 4型地物光谱仪,其光谱分辨率为3 nm,采样波长范围为300~2 500 nm。为了减弱观测角度和太阳天顶角对测量结果的影响,每次光谱测量时间均为北京时间11:00—12:30,且在数据测试前通过标准BaSO4参考板对冠层辐亮度数据进行校正。测量时探头高度距离小麦冠层1.3 m,每个区域重复测量10次,取其平均值作为本次小麦冠层辐亮度。然后计算反射率,计算式为
(1)
式中ρ——冠层反射率
Ltarget——目标辐亮度,μW/(cm2·nm·sr)
Lboard——参考板辐亮度,μW/(cm2·nm·sr)
ρboard——参考板反射率
1.2.2病情指数调查
冠层光谱测量的同时采用5点取样法调查小麦条锈病病情严重度,在每个样方内选取对称的5点,每点调查30株小麦的单叶病情严重度,并将其分为9个级别,即:0、1%、10%、20%、30%、45%、60%、80%和100%,通过记录各严重度小麦叶片数计算病情指数[33],计算式为
(2)
式中DI——病情指数
t——各梯度级别
m——最高梯度
f——各梯度叶片数
1.2.3冠层SIF提取
冠层SIF提取方法主要包括基于辐亮度数据的直接提取算法和基于反射率数据的间接提取算法两种。基于辐亮度的冠层SIF直接提取算法是利用夫琅和费暗线原理,通过FLD(Fraunhofer line discrimination)、3FLD(3 bands FLD)以及iFLD(Improved FLD)等算法[34]估测SIF强度。已有研究表明,FLD算法在一定程度上会高估荧光值,iFLD和3FLD方法则能够得到较为可靠的荧光估测结果[35],而3FLD算法较iFLD算法更稳健[36-37]。因此,本文利用3FLD方法估算O2-A波段(760 nm)冠层SIF的绝对强度,计算式为
(3)
其中
ωleft=(λright-λin)/(λright-λleft)
(4)
ωright=(λin-λleft)/(λright-λleft)
(5)

λin、λleft、λright——吸收线内、左、右波段波长
ωleft、ωright——吸收线左、右两参考波段权重
Iin、Ileft、Iright——吸收线内、左、右波段的太阳辐照度,μW/(cm2·nm)
Lin、Lleft、Lright——吸收线内、左、右波段的植被冠层反射辐亮度,μW/(cm2·nm·sr)
除了利用夫琅和费吸收线直接提取冠层SIF外,基于反射率比值的方法也可获取650~800 nm波段的荧光信息,是提取冠层SIF强度的间接方法[38]。基于反射率比值提取冠层SIF主要是利用荧光对650~800 nm波段范围内反射率的影响,获取与叶绿素荧光相关的光学指数,包括反射率比值荧光指数、反射率导数荧光指数和填充指数3种[39]。反射率比值荧光指数通过对680 nm或740 nm附近受荧光影响强的波段和一个受荧光影响较少或不受影响波段的比值运算,消除反射率信息,获取荧光强度。反射率导数荧光指数利用反射率一阶导数的比值反映荧光信息,能够增强荧光对反射率的影响,突出由荧光引起的细微变化。填充指数通过两个波段反射率的差间接反映荧光信息,但该指数受夫琅和费暗线的深度和荧光大小的共同影响,由于大气和太阳观测几何的变化都会影响夫琅和费暗线的深度,所以该指数仅适用于在相同时间和观测条件下的数据对比[40]。
1.2.4吸收特征参数计算
吸收特征是植物组织结构、色素含量、水分和蛋白质中各种基团对反射光谱响应的重要特征[33]。反射率光谱中的细微吸收特征能够在连续统去除的归一化过程中得到增强[41]。连续统是指将光谱曲线上凸出的“峰”值点用直线连接,并使所形成的折线在峰值点上的外角大于180°[42],连续去除后的光谱反射率计算式为
(6)
式中ρc——连续统线
原始光谱经过连续统去除后,波长起点与终点相对反射率等于1,处于起点与终点间的波长,其反射率都小于1。本文在小麦冠层反射率光谱连续统去除基础上参照文献[43-45]提取了吸收峰深度(H)、吸收波长位置(P)、吸收峰面积(A)、吸收峰左面积(A1)、吸收峰右面积(A2)、对称度(S)和面积归一化吸收深度(NMAD)等特征参量。
吸收峰深度H计算式为
H=1-ρ′min
(7)
式中ρ′min——连续统去除后的最小反射率
吸收波长位置P计算式为
P=λH
(8)
式中λH——吸收峰深度对应的波长
吸收峰面积A计算式为
(9)
式中a——吸收带起始波长
b——吸收带终止波长
di——吸收深度
Δλ——波长增量
吸收峰左面积A1计算式为
(10)
吸收峰右面积A2计算式为
(11)
对称度S计算式为
S=A1/A
(12)
面积归一化吸收深度NMAD计算式为
NMAD=H/A
(13)
1.3 GA-SVR算法
1.3.1SVR算法
SVR算法的基本思想是利用训练样本建立一个回归超平面,将样本逼近超平面以使样本点到该平面的总偏差达到最小[46],其计算式为
(14)
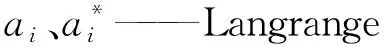
β——偏置φ——映射函数
为避免高维内积运算,引入核函数k(xi,x)代替(φ(xi),φ(x)),则式(14)转换为
(15)
SVR算法常用的核函数有线性核函数、径向基(Radial basic function,RBF)核函数、多项式核函数以及Sigmoid核函数等[47]。相较于线性核函数仅能处理线性问题,RBF核函数可处理自变量与因变量之间复杂的非线性问题。此外,应用RBF核函数的效果通常优于多项式核函数与Sigmoid核函数,并且需要设置的参数更少[48]。因此,本文在基于GA-SVR算法构建小麦条锈病严重度估测模型时采用了RBF核,其计算式为
(16)
式中g——核参数
1.3.2GA
GA是一种模拟自然选择和自然遗传的随机搜索与最优化求解方法,它将具体的求最优解问题进行编码转换为特定数量并具有基因序列的种群,其中种群中的每一个体代表每一个解,以适应度函数评价种群中个体的求解结果,并根据个体的适应度,进行选择、交叉和变异3种遗传操作,以保证在进化过程中种群的适应性不断增强,进而实现个体的优胜劣汰,获取问题的最优解[49](图1)。

图1 遗传算法流程图Fig.1 Flow chart of genetic algorithm
1.3.3基于GA-SVR算法的特征优选
利用GA-SVR算法优选模型特征参量是基于二进制编码方法对初始群体中的个体染色体进行编码(图2),图中每个染色体由3部分构成,第1部分C1-Cx与第2部分g1-gy分别为惩罚参数C与核参数g的二进制编码,其中下标x和y表示惩罚参数C与核参数g的二进制位数,决定解码为十进制数的精度。第3部分f1-fz为所有特征集合的编码,下标z为特征总个数。当编码中的二进制数为“1”时表示该特征被选中,为“0”时表示该特征未被选中。

图2 编码示意图Fig.2 Coding diagram
基于GA-SVR算法进行特征优选时,需要对种群数量、最大迭代次数、交叉概率和遗传概率等参数进行设置。为了保证遗传算法具有全局搜索能力,在上述遗传参数设置的基础上按 “单点交叉”方式对种群中的个体进行两两交叉,同时以基本位变异的方式依据较小的变异概率对交叉完成后的个体进行变异操作,以防止算法陷入局部最优。经过选择-交叉-变异等遗传操作形成子代种群,重复进行解码、适应度评价、种群更新等步骤,在满足迭代终止条件时算法停止。
1.4 模型构建与评价指标
为了保证评价结果的稳定性和可靠性,提高模型的泛化能力,减弱样本数据对评价结果的影响,本文将52个原始样本重复进行3次随机分组(记为a、b、c 3组),每组按照3∶1的比例随机划分为训练集和验证集,其中39个训练样本用于特征选择与模型构建,13个验证样本用于模型评价。
选用预测值和实测值之间的决定系数R2与均方根误差(RMSE)2个指标进行模型精度评价,其中决定系数R2越大,均方根误差(RMSE)越小,预测样本与实测样本偏差越小,模型精度越高。
2 结果与分析
2.1 特征参量优选
特征参量很大程度上影响了模型的性能,为了提高小麦条锈病遥感监测精度,利用反射率光谱数据在作物生化参数探测方面的优势和SIF在光合生理诊断方面的优势,计算了吸收深度等7个反射率光谱吸收特征及15个冠层SIF数据,利用封装法将GA和SVR算法相结合进行小麦条锈病遥感监测特征参量优选,并将其与CC特征优选方法进行对比,分析两种方法提取特征参量所建模型精度,以确定遥感探测小麦条锈病的敏感因子及模型。
2.1.1CC特征优选
CC是一种过滤性的特征选择方法,具有计算量小及所选特征参量通用性较好的优点。本文在计算冠层SIF及反射率吸收特征参数与病情严重度间相关系数的基础上,挑选达到0.001极显著水平的特征参量作为遥感监测小麦条锈病严重度的敏感因子。
(1)冠层SIF强度特征参量
分别利用辐亮度和反射率计算了小麦条锈病不同病情下的冠层SIF信息。利用辐亮度数据计算冠层SIF时,由于O2-A (760 nm)波段氧气吸收形成的夫琅和费暗线特征明显[50],荧光估测精度高[51],因此本文利用辐亮度基于3FLD方法估测了760 nm处的SIF强度,并将计算得到的SIF绝对强度除以夫琅和费吸收线内的太阳入射辐照度,获取O2-A波段的SIF相对强度,以消除太阳光照强度等外界因素对叶绿素荧光提取结果的影响[52-53]。
(17)
式中F′——SIF相对强度
利用反射率间接估测冠层SIF时,由于填充指数法仅适用于在相同时间和观测条件下的数据对比,因此本文仅计算了反射率比值荧光指数和反射率一阶导数荧光指数。目前常用的反射率比值荧光指数主要有ZARCO-TEJADA等[54-55]提出的


表1 冠层SIF与病情指数相关系数(n=52)Tab.1 Correlation coefficient between canopy SIF and disease index (n=52)
(2)反射率吸收特征优选
在对400~550 nm和550~770 nm两个吸收波段范围内的反射率光谱数据进行连续统去除的基础上提取了吸收位置等光谱吸收特征参数,并计算其与小麦条锈病严重度的相关性(表2)。由表2可以看出,在400~550 nm和550~770 nm 2个吸收波段范围内共有吸收位置(P)、最大吸收深度(H)以及面积归一化最大吸收深度(NMAD)等9个特征参量与小麦条锈病严重度达到了0.001水平的极显著相关,可以作为遥感监测小麦条锈病严重度的模型输入变量。
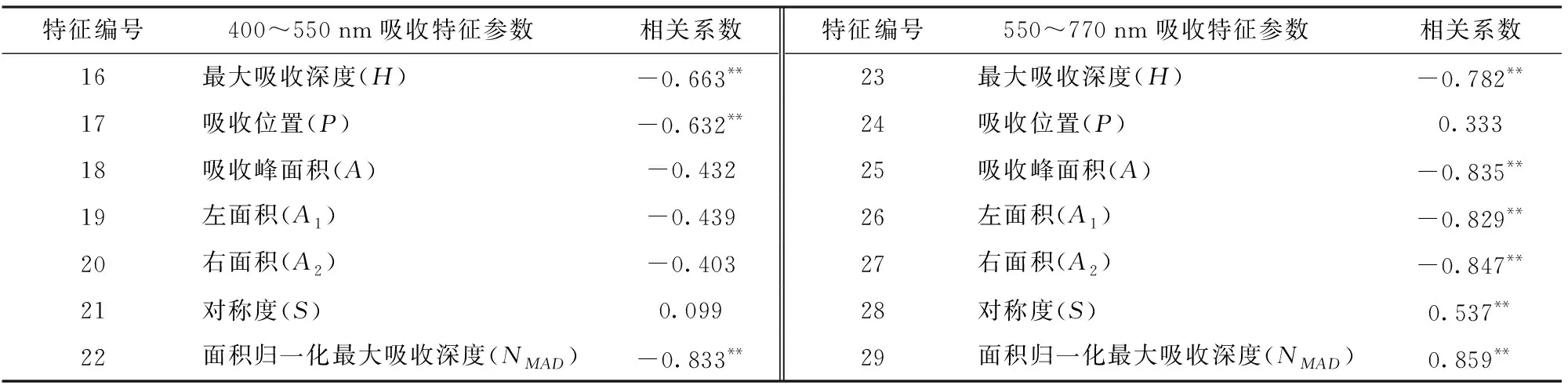
表2 吸收特征参数与病情指数相关系数(n=52)Tab.2 Correlation coefficient between absorption characteristics and disease index (n=52)
2.1.2GA-SVR特征优选
利用GA-SVR算法优选遥感监测小麦条锈病敏感因子时,GA及SVR参数设置对迭代寻优的速率与准确率有较大的影响,基于此本文通过对训练样本的多次仿真确定SVR算法中惩罚参数C与核参数g的寻优范围及GA各参数设置(表3)。然后在上述参数设置的基础上将GA-SVR特征选择算法独立运行20次,单次运行最大迭代次数设定为100,以训练集10折交叉验证均方误差(Mean square error,MSE)作为评价个体优劣的适应度,其中适应度最小的个体所对应的特征参量以及惩罚参数C和核参数g即为GA-SVR模型构建时的最优特征集合以及SVR算法的最佳参数组合。表4为a组数据运行20次得到的不同适应度及其对应的最优特征集合。
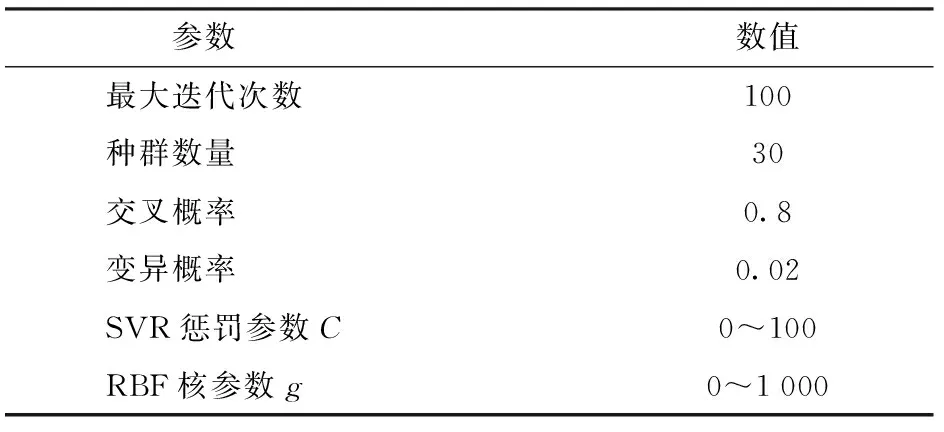
表3 GA-SVR各参数设置Tab.3 GA-SVR parameter settings

表4 a组数据单次适应度最小值及其对应特征与参数组合Tab.4 Minimum single fitness of group a of data and their corresponding characteristics and parameter combinations
由表4可知,第8次运行时的适应度为GA-SVR算法20次运行中的最佳适应度,对应的惩罚参数C(94.937 9)与核参数g(0.967 0)为SVR算法的最优参数组合,特征集合{4,5,17,22,24,25,27}为遥感监测小麦条锈病严重度的最佳特征参量。同理得到b组和c组的最优特征集合及SVR算法的最优参数组合(表5)。
2.2 模型构建和精度评价
2.2.1模型构建
基于GA-SVR算法优选的最优特征组合建立遥感监测小麦条锈病严重度的GA-SVR模型(图3),并将其与CC法算法优选的特征参量集合所建的CC-SVR模型(图4)进行对比分析。

表5 3组数据GA-SVR优选特征组合及参数组合Tab.5 Three sets of data GA-SVR preferred feature combination and parameter combination
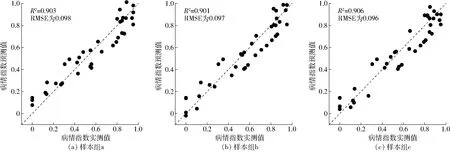
图3 GA-SVR模型训练集预测结果(n=39)Fig.3 GA-SVR model prediction result on training set(n=39)

图4 CC-SVR模型训练集预测结果(n=39)Fig.4 CC-SVR model prediction result on training set(n=39)
由图3、4可以看出,3个样本组中GA-SVR模型预测DI值和实测DI值之间的R2均在0.9以上,相对于同组CC-SVR模型分别提高了9.9%、10.0%、5.6%,RMSE分别降低了26.3%、26.5%、19.3%,GA-SVR模型对小麦条锈病严重度的估测精度优于CC-SVR模型。说明将GA-SVR模型优选的特征作为模型输入能够明显地提高模型对训练集病情指数的预测能力,而CC法优选的特征虽然对病情指数敏感,但从CC-SVR模型对训练集病情指数的预测精度来看,其并非为SVR模型的最佳输入特征。
2.2.2模型评价
为了在样本数量有限的情况下更客观地评价模型精度,尽可能减少“过拟合”问题对模型评价结果的影响,采用能够充分利用样本中所有数据的保留样本交叉检验方式对CC分析法以及GA-SVR方法所选特征构建的小麦条锈病严重度预测模型进行评价(表6)。由表6可以看出,3组验证样本中GA-SVR模型的预测精度较同组CC-SVR模型均有不同程度的提高,其中GA-SVR模型估测DI值和实测DI值间的R2较同组CC-SVR模型至少提高了2.7%,平均提高了17.8%,RMSE较同组CC-SVR模型至少减少了10.1%,平均减少了32.1%。综合分析图3、图4和表6可知,无论是训练集样本还是验证集样本,GA-SVR模型对DI的预测能力均优于CC-SVR模型,将特征优选和模型构建相融合的GA-SVR模型能够提高小麦条锈病严重度的预测精度,且模型稳定性和泛化能力均优于CC-SVR模型,更适合于小麦条锈病严重度的敏感因子优选与模型构建。这是因为CC算法是以显著检验水平作为特征优选的条件,仅考虑了特征参量与病情严重度之间的相关性,没有考虑不同特征参量之间是否存在数据的冗余以及所选的特征参量是否最适合于模型构建算法,影响了模型的预测精度。而GA-SVR算法综合利用了GA的全局搜索特点和SVR算法较优的学习能力,考虑了SVR参数对特征参量优选的影响,将所有特征与SVR参数进行联合编码,以10折交叉验证最小MSE作为特征与参数的优选依据,对所有可能选择到的特征进行有向搜索,保证了所选特征的敏感性,提升了模型的预测精度。

表6 小区试验数据验证结果(m=13)Tab.6 Verification results of plot experiment (m=13)
2.2.3大田调查数据验证
2018年5月12日于陕西省汉中市宁强县大田小麦种植区域调查条锈病的发病状况,利用ASD Field Spec 4型地物光谱仪同步获取42个对应样本点的冠层光谱数据,并基于此数据对本文所建立的模型进行验证(表7),以评价模型的可靠性与普适性。

表7 大田调查数据验证结果(m=42)Tab.7 Verification results of field survey data (m=42)
由表7可知,3个样本组建立的GA-SVR模型预测DI值与实测DI值间的R2均高于0.7,比CC-SVR模型至少提高了66.2%,RMSE均不高于0.150,比CC-SVR模型至少减少了31.5%,联合GA与SVR算法的特征优选方法能够提高小麦条锈病的遥感探测精度,GA-SVR模型具有较好的可靠性和普适性。
3 讨论
融合GA和SVR算法优选小麦条锈病遥感监测的敏感因子时,3个样本组中优选的特征参量的一致性不高,说明GA-SVR方法进行特征选择时,受到原始样本的影响较大。这是因为封装法是以模型的精度作为特征优选的标准,样本的差异影响交叉验证的精度,小样本训练集的随机划分难以代表所有样本间的差异,进而导致3个样本组所选的特征参量不一致,能否利用大量的训练样本解决这一问题还有待继续研究。
本文协同冠层SIF数据和反射率光谱进行小麦条锈病遥感监测时,反射率数据仅利用了对植被叶绿素含量敏感的可见光波段的吸收特征,而小麦在受到条锈病菌侵染时,水分、花青素等生化组分含量也会发生相应的变化[58]。在构建小麦条锈病严重度反演模型时,若增加能够反映各种生化组分的光谱指数,分析不同光谱指数对条锈病害胁迫的响应特性,能否提高小麦条锈病的遥感监测精度还有待进一步研究。
综合利用反射率光谱在作物生化参数探测方面的优势及SIF在光合生理诊断方面的优势构建了小麦条锈病严重度估测模型,并没有考虑反射率吸收特征和SIF数据对模型的贡献率问题,如何量化反射率光谱数据和SIF数据对遥感监测小麦条锈病严重度的贡献率,确定各个输入特征在模型中的权重,进一步提高小麦条锈病的遥感监测精度,则是一个值得研究的问题。
在利用SVR算法构建小麦条锈病严重度估测模型时,仅考虑了高斯核函数,并没有分析所选特征参量与小麦条锈病严重度之间的映射关系,确定不同特征参量与病情严重度之间的最优映射函数进而提高小麦条锈病严重度的遥感估测精度则是下步要研究的问题。
本文在构建小麦条锈病严重度反演模型时,仅选用了对小样本适用性较好的SVR算法,并未与其它机器学习算法进行对比分析。已有研究将GA与随机森林算法结合进行敏感波段的选择,并取得了较好的研究成果[18],但是将GA与其他机器学习算法结合进行小麦条锈病敏感特征选择能否改善小麦条锈病严重度反演精度还需进一步研究。
4 结束语
基于小麦条锈病不同病情严重度下的冠层SIF数据与反射率吸收特征参量,分别利用GA-SVR算法与CC算法优选了小麦条锈病遥感监测的敏感因子,在此基础上构建了小麦条锈病的遥感监测模型。结果表明,GA-SVR算法优选的小麦条锈病遥感监测的敏感因子为7~8个,而CC分析法则优选出了22个因子,GA-SVR算法极大地降低了特征空间的维度,减少了特征参量间的冗余,降低了模型的复杂性。从模型的预测性能来看,无论是小区试验数据还是野外大田数据,GA-SVR模型的预测精度均高于CC-SVR模型。以小区试验数据为验证样本时,GA-SVR模型预测DI值与实测DI值之间R2均在0.9以上,RMSE均小于0.1,比CC-SVR模型的R2至少提高了2.7%,RMSE至少降低了10.1%。以大田数据为验证样本时,GA-SVR模型预测DI值与实测DI值间的R2比CC-SVR模型至少提高了66.2%,RMSE至少降低了31.5%。
