力矩受限双臂空间机器人轨迹跟踪与控制

时 存，古思勇，王 莹

（1.郑州电力高等专科学校，河南 郑州 450000；2.厦门理工学院，福建 厦门 361000）

1 引言

在复杂未知的太空环境中，机器人由于其能代替宇航员执行一些较为危险的在轨操作，近年来得到国内外航天研究人员广泛关注，并已实际应用于空间站建设、卫星在轨维修、太空目标捕获等任务。而双臂机器人因其具有更好的操作性、灵活性和精确度，在应用范围和发展前景上较单臂机器人更广，因此逐步成为空间机器人项目的研究热点[1-4]。

与地面机器人不同，空间机器人由于处于失重环境而呈现基座不受外力作用的自由漂浮状态，机械臂与基座之间耦合，使得其动力学建模、轨迹规划和运动控制更为复杂，引起国内外学者的广泛研究[5-8]。

文献[9]通过建立参数线性化的空间机器人动力学模型，把空间机器人控制问题转化为类似地面固定基座机器人控制问题，设计了一种关节空间PD 控制器，实现了机械臂关节轨迹跟踪控制；文献[10]利用神经网络的非线性逼近特性、并行分布处理能力及学习适应能力，设计了一种神经网络控制器，实现了空间机器人的轨迹跟踪任务；文献[11]设计了一种轨迹跟踪自适应控制方法，在保证控制系统鲁棒性的同时，解决了参数不确定性的问题，并降低了数据计算量。然而上述研究均只能在理论上实现对机械臂的有效控制和轨迹跟踪，未考虑实际工程中各关节控制力矩输出受限和能量优化的问题，有待进一步研究。

针对双臂空间机器人（Dual-Arm Free-Floating Space Robot）机械臂关节控制力矩受限条件下的轨迹跟踪控制问题，设计了一种基于状态依赖Riccati 方程的优化控制器。在建立机器人动力学模型的基础上，首先，借助增广变量法，将系统动力学方程扩展描述成以各关节角度和角速度为状态变量的伪线性表达形式，获得 SDC（State-dependent Coefficient）矩阵；由此，基于状态依赖Riccati 方程，选取一组合适的权值矩阵，设计优化跟踪控制器；进而，在控制器中加入饱和约束，以解决实际应用过程中关节控制器输入力矩幅值受限的问题；SDRE 稳定性引理保证了所设计控制器的渐进稳定性，并通过数值仿真，验证所设计控制器的有效性。

2 动力学建模

DFFSR 系统由一个不受外力作用的自由漂浮基座（忽略微重力环境）M0及四个机械臂 M1、M2、M3、M4组成，如图 1 所示。设该系统各关节均主动受控，且在同一平面运动，建立各分体Mi（i=0，1，2，3，4）的主轴坐标系为 xi轴的基矢量，其中：O0与 M0的质心 Oc0重合，O1，O2，O3，O4分别为连接M1与 M0、M2与 M1、M3与 M0、M4与 M3的 转 动 幅 中 心 ，xi（i=1，2，3，4） 为机械臂的对称轴。设轴上与O1的距离为l0，M（ii=0，1，2，3，4）沿轴的长度为l（ii=1，2，3，4）；质心Oci在轴上与Oi的距离为a（ii=1，2，3，4）；各分体的质量和中心惯量张量分别为mi和Ji，M=Σm（ii=1，2，3，4）为系统总质量，O为系统总质心。

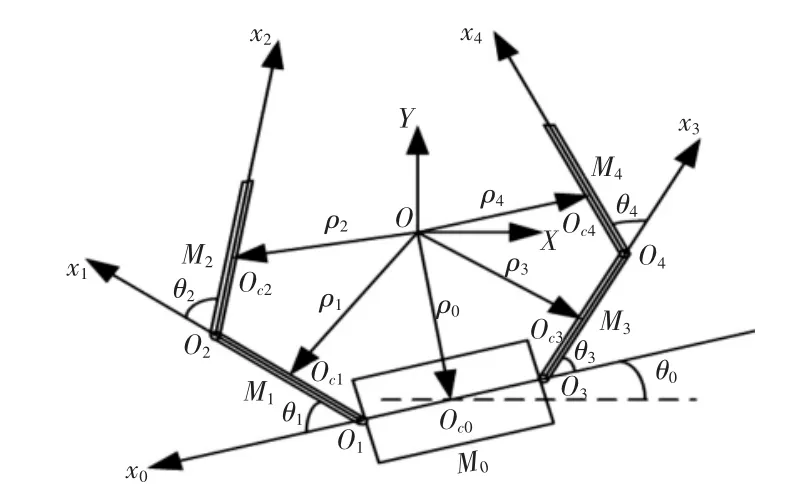
图1 DFFSR 系统结构图Fig.1 System Topology of DFFSR

由系统的动量守恒关系及Lagrange 第二类方程，可导出自由漂浮状态下，该系统的动力学方程[12]：

为了克服初始误差带来的较大冲击力矩的影响，并使得机械臂各关节控制器输出力矩始终保持在一可控范围内，可在控制器末端引入双曲函数：

使得输出力矩满足饱和约束特性：

联立式（1）、式（2），则可得到力矩受限条件下的动力学方程：

动力学方程式（1）具备如下性质：

（1）惯性矩阵 M（q）∈R4×4为对称正定矩阵。

3 相关知识介绍

考虑仿射非线性系统：

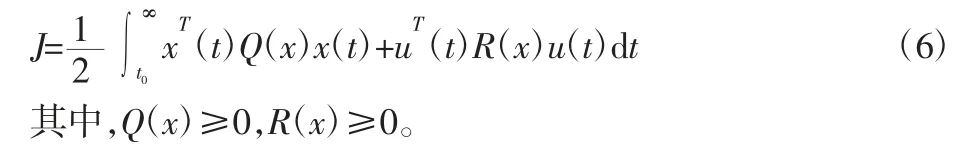
当式（5）满足：f（0）=0 且在正常的取值范围内，f（x）具有一阶连续微分时，可将该状态方程转化为状态依赖参数SDC（Sdate Dependent Coefficient）的类线性结构方程[13]：

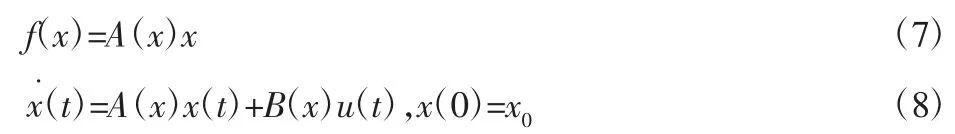
当式（8）中的SDC 矩阵 A（x）和 B（x）满足｛A（x），B（x）｝逐点可控且｛A（x），Q1/2（x）｝逐点可观时，则针对由非线性状态方程（5）和性能指标函数（6）描述的无限时间状态调节问题，可设计局部渐进稳定优化控制律为[14]：

式中：P（x）满足代数 Riccati 方程：

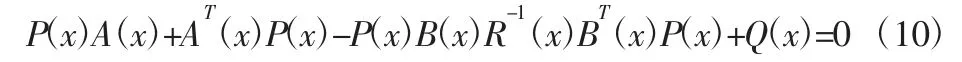
4 考虑力矩受限的优化控制器设计

证明（1）将空间机器人动力学方程式（4）转化为状态方程的标准表达形式：

选取关节角度和角速度x=［x1x2］作为系统的增广变量，则该系统的状态方程变为：

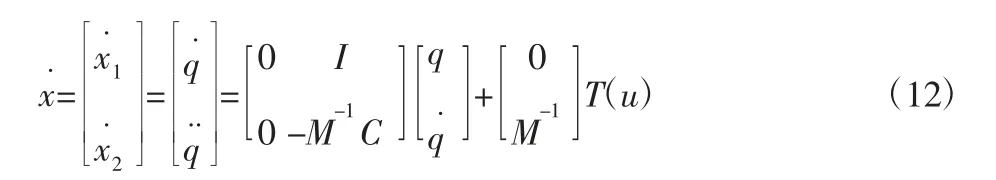
从上式中直接获得SDC 矩阵为：

则由性质（1）可知空间机器人惯性矩阵M 为对称正定矩阵，可得出｛A（x），B（x）｝满足逐点可控条件；

（2）由于权值矩阵Q（x）为一组可调整的常值矩阵，因此总能通过选取合适的 Q（x）阵，使得｛A（x），Q1/2（x）｝满足逐点可观条件。证毕。

将式（12）描述的类线性问题可转化为SDRE 参考轨迹积分跟踪问题，选取优化指标为：

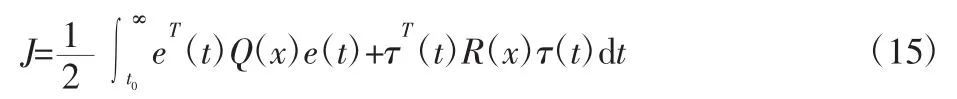
则由引理2 可设计优化跟踪控制律为：

进一步由式（2）可得力矩受限条件下的跟踪控制律为：

式中：τmax—所设定的机械臂各关节最大输出力矩；qd—双臂空间机器人系统机械臂各关节在关节空间的期望运动轨迹，P（x）满足代数Riccati 方程：

Remark 1.定理1 证明所设计的控制律式（17）满足局部渐进稳定性。

选取状态误差权值矩阵Q（x）和控制力矩权值矩阵R（x）均为对角正定常值矩阵，且由性能指标函数式（12）可以看出，当Q（x）矩阵权对应的对角元素越大时，跟踪误差越小，但输出控制力矩较大；当R（x）矩阵权对应的对角元素越大时，输出控制力矩就较小，而跟踪精度就变低。

5 仿真实例与分析

以文中所提DFFSR 为对象，具体惯性参数，如表1 所示。

表1 模型参数Tab.1 Model Parameters

设DFFSR 系统机械臂各关节在关节空间的期望运动轨迹为：

系统运动的初始值为：

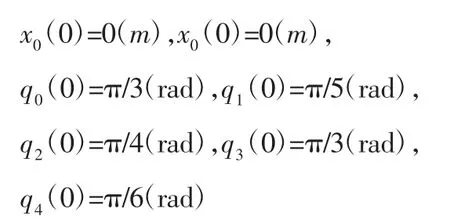
选取权值矩阵：

仿真算例1.不考虑机械臂各关节输出力矩受限情况，使用控制律式（16）对机械臂轨迹跟踪运动情况进行仿真，总时长为20s。仿真算例2.考虑机械臂各关节输出力矩受限情况，使用控制律式（17）对机械臂轨迹跟踪运动情况进行仿真，整个追踪过程耗时 20s。综合图 2（a）、图 2（b）和图 4（a）和图 4（b）来看，所设计的SDRE 控制器能够使DFFSR 系统各关节实现对期望轨迹的跟踪；对比图2（c）和图4（c），可以看出改进后的控制器稳定性更好，跟踪误差保持在±0.01rad 以内，且具有一定抗干扰能力；对比图 3（a）、图 3（b）和图 5（a）、图 5（b）），可以看出在加入力矩饱和约束后，能有效克服初始误差带来的较大冲击力矩的影响，使得输出力矩保持在一可控范围内。从对比试验结果可以看出，相比于不考虑力矩受限的情况，所设计的优化控制器以牺牲一定的跟踪速度为代价，在保证跟踪误差保持在一较小范围的前提条件下，有效的克服了初始冲击力矩过大的缺陷，具有较强的理论意义和实际价值。

图2 DFFSR 轨迹跟踪结果Fig.2 Trajectory Tracking Result of DFFSR

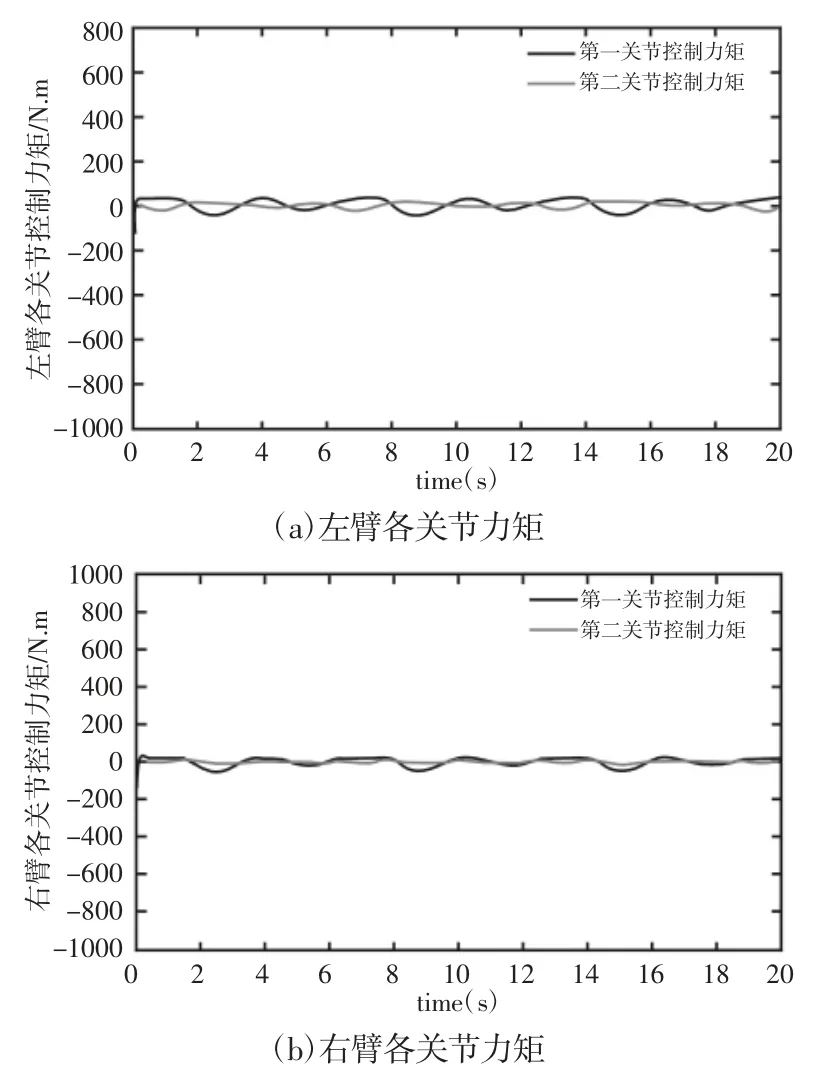
图3 DFFSR 各关节力矩Fig.3 Control Torque of DFFSR

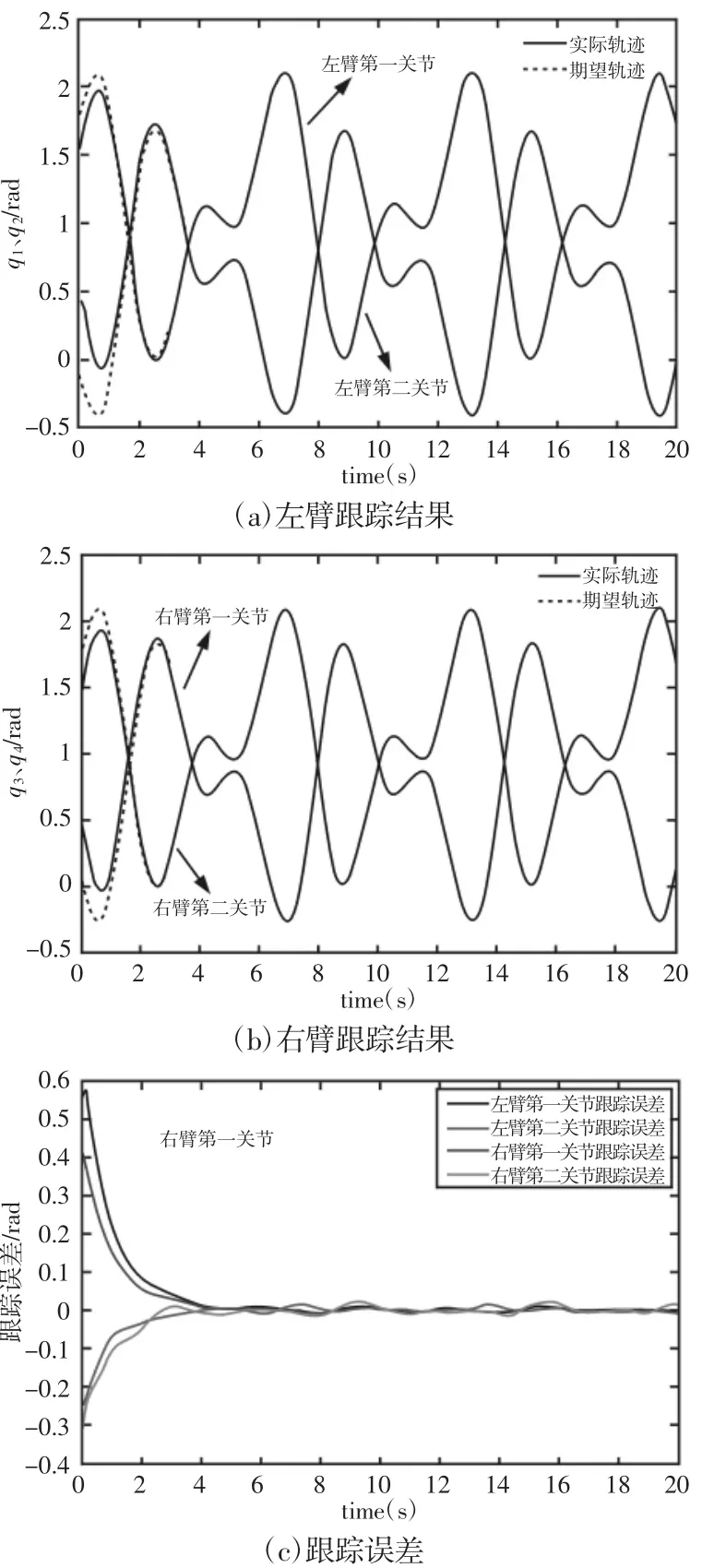
图4 DFFSR 轨迹跟踪结果Fig.4 Trajectory Tracking Result of DFFSR

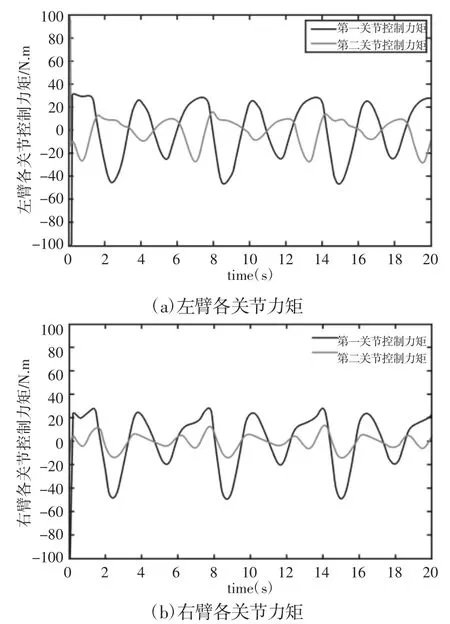
图5 空间机器人系统各关节输出力矩Fig.5 Control Torque of Each Joints on Space Robot System

6 结论

考虑DFFSR 系统的关节轨迹跟踪控制问题，设计了一种SDRE 优化控制方法，能够在保持系统稳定的同时，优化各关节控制力矩，同时为了克服由初始误差带来的冲击力矩，在控制器中加入饱和约束，解决了实际应用过程中关节控制器输出力矩受限问题，数值仿真验证了所设计控制器的稳定性。