6-DOF 抛光工业机器人关节空间轨迹规划研究

王 川，金晓怡，陈志鹏，叶黎杰

（上海工程技术大学机械工程学院，上海 201620）

1 引言

近年来，在生产加工自动化中，为提高工件抛光精度和生产效率，抛光机器人的应用越来越广泛[1]。机器人在执行抛光加工任务时，需考虑运动位移、速度和加速度等约束条件，这属于轨迹规划的研究内容。机器人轨迹规划分为笛卡尔空间与关节空间的轨迹规划，由于关节空间轨迹规划计算量小，能有效避免机器人的奇异性问题，所以常被采纳[2]。运动轨迹规划的好与坏直接影响抛光零件的质量。文献[3]采用五次多项式进行手术机器人关节空间轨迹规划，并用平均法确定角速度和角加速度；文献[4]在关节空间分别研究通过起点和终点的三次、五次和七次多项式插值算法，发现多项式次数越高，轨迹精度越高，但计算量大且容易出现“龙格现象”；文献[5]采用五次多项式进行关节空间轨迹规划，对比三次多项式，角速度和角加速度更加光滑，但没有考虑中间点角速度优化；工业机器人在生产操作中，经过加工路径中间点时关节速度往往不为零，这就需要充分考虑中间点角速度的确定。

以六自由度抛光工业机器人为研究对象，采用五次多项式进行关节空间轨迹规划，通过三次多项式与五次多项式函数的插值结果进行标定，表明五次多项式插值更加优越。同时，对五次多项式插值算法的约束条件中间点角速度的设置方法提出改进，采用角速度加权值作为中间点瞬时角速度的估计值，在MATLAB 上进行仿真，验证该角速度约束条件下轨迹规划算法的有效性和可靠性。

2 抛光工业机器人结构

IRB1600 机器人由基座、腰部、大臂、肘部、小臂、手腕6 个部分组成，具体结构，如图1 所示。该机器人属于6 自由度关节型工业机器人，且6 个关节均为旋转关节，能够在可达空间内按照示教或规划指令进行定位和调姿，完成工件的搬运或抛光等工作。

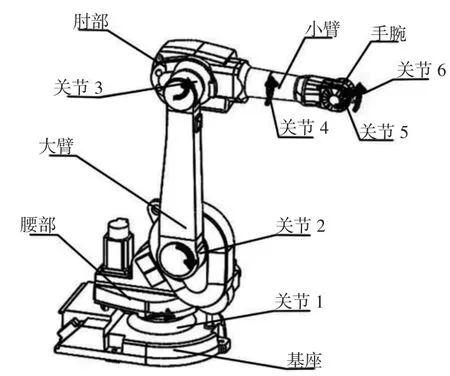
图1 抛光机器人结构图Fig.1 Structure of the Polishing Robot

3 关节空间轨迹插补算法

首先利用逆运动学将已知的笛卡尔空间路径点转化为各个关节角度值，采用三次、五次多项式对各个关节角进行插值得到相应的关节轨迹曲线，每个关节时间函数是相互独立的，但总运动时间相同。假设起始点t=0 时刻的关节角度为θ0，终点t=tf时刻的关节角度为θf。

3.1 五次多项式插值[6]

关节插值函数为：

各关节角度、角速度、和角加速度在起点和终点满足的约束条件为：

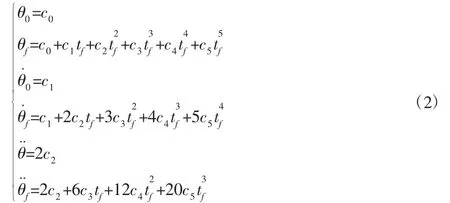
求解方程组（2）得五次多项式插值系数为：

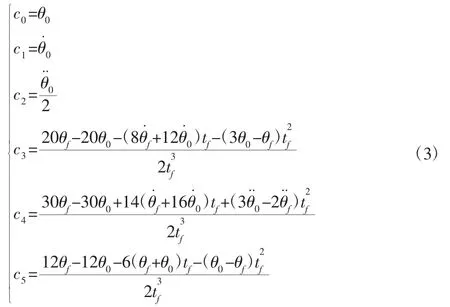
3.2 角速度设置方法

在关节空间中采用适当的启发式方法，由控制系统自动选择路径点的速度[7]，常采用的是取相邻两段运动轨迹角速度平均值作为中间路径点的瞬时角速度，对此方法进行改进，取相邻两段运动轨迹平均角速度的加权值作为中间路径点的瞬时角速度，角加速度由系统根据角速度变化自适应产生。

4 MATLAB 仿真实验

4.1 机器人建模

通过D-H 参数法建立抛光工业机器人数学模型，如表1 所示。利用MATLAB Robotics Toolbox 建立机器人连杆模型，如图2所示。

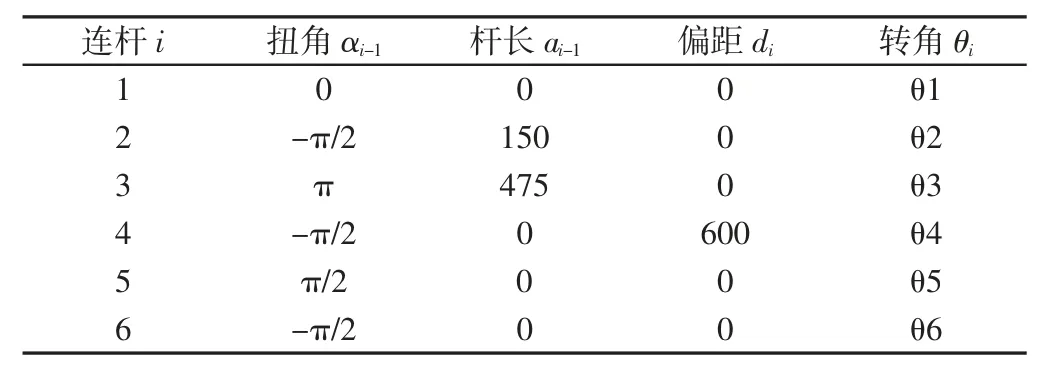
表1 抛光机器人D-H 参数表Tab.1 D-H Parameter List of the Polishing Robot

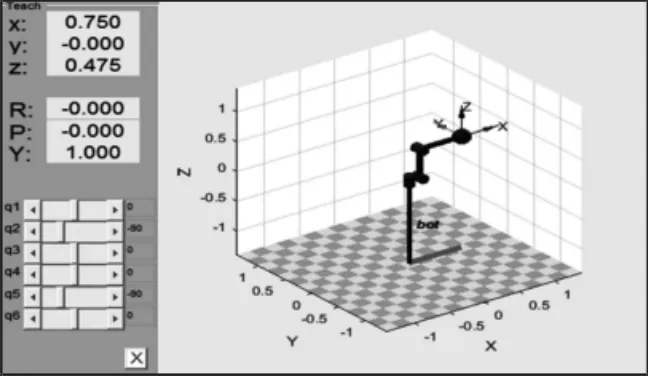
图2 机器人连杆模型Fig.2 Link Model of the Robot

4.2 针对特定工件的轨迹规划仿真

将手表表壳的表耳部分作为抛光加工面，如图3 蓝色部分所示。利用Pro/E 软件，在待抛光曲面宽度中心选取10 个点为路径关键点，如表2 所示[8]。

图3 表壳表耳部分拟抛光曲面Fig.3 Surface to be Polished of the Ear on the Watch Case

表2 目标路径上选取的关键节点数据Tab.2 Key Points Chosed from the Target Path

利用MATLAB 软件[9]，将直角坐标空间每个节点的坐标求逆解转化为关节空间中每个节点的关节角度值。设定起点和终点的角速度和角加速度为零，相邻两个节点之间的时间间隔为1s，总运动时间为9s。利用三次、五次多项式插值算法对上述点进行插值，分别得到运动过程中6 个关节的关节角度、角速度和角加速度变化情况，如图4 所示。由于篇幅原因，此处以关节2 为示例。其中实线为三次多项式规划曲线，虚线代表五次多项式规划曲线。

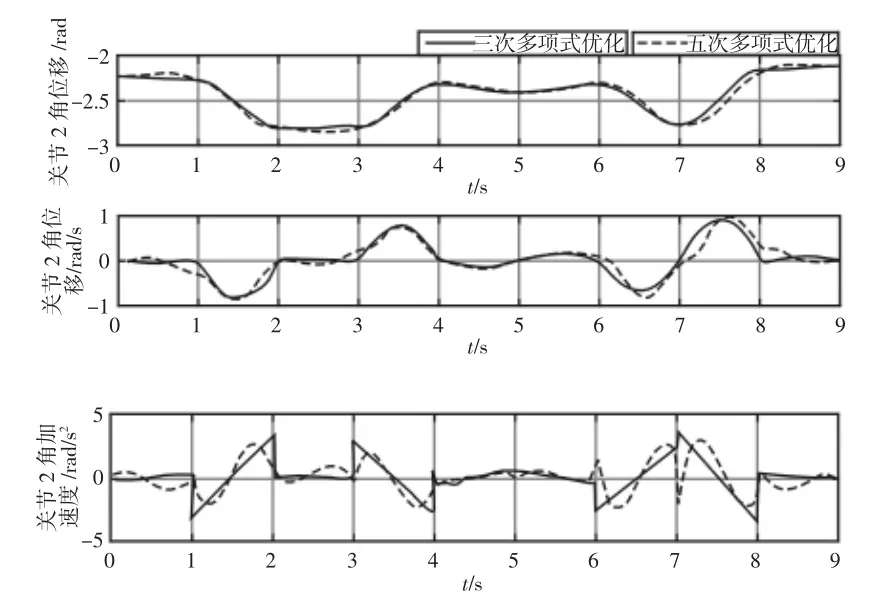
图4 三次多项式与五次多项式规划后关节2 各曲线Fig.4 Curves of Joint Two After Cubic Polynomial Planning and Quintic Polynomial Planning

由图4 可知，三次多项式插值算法规划的关节2 角度和角速度曲线光滑连续，三次多项式插值算法规划的关节2 角加速度曲线突变且不光滑，易对驱动电机造成损坏。五次多项式插值算法规划的关节2 角加速度光滑连续，运动较为平稳。但是角速度最大为0.906rad/s，角加速度最大达到2.859rad/s2，其它关节角速度、角加速度值更大，因此需要对角速度的约束条件进行优化，取相邻两段运动轨迹角速度的加权平均值作为中间点瞬时角速度，各关节角度、角速度和角加速度曲线对比，如图5～图7 所示。角速度和角加速度最大值，如表3 所示。其中实线为角速度加权优化曲线，虚线代表角速度平均优化曲线。

图5 各关节角位移对比曲线Fig.5 Comparison Curves of Angular Position of Different Joints

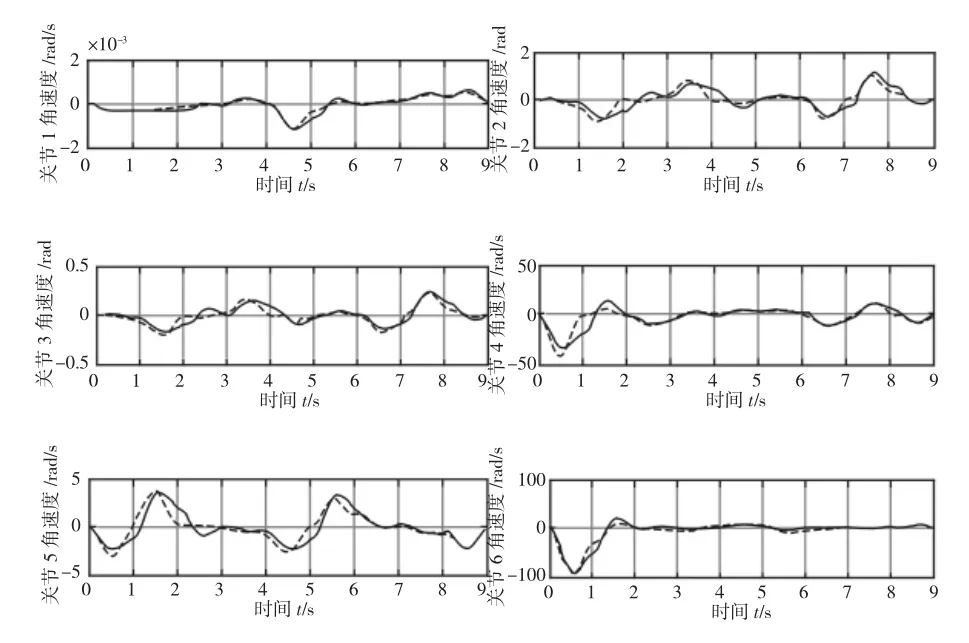
图6 各关节角速度对比曲线Fig.6 Comparison Curves of Angular Velocity of Different Joints

图7 各关节角加速度对比曲线Fig.7 Comparison Curves of Angular Acceleration of Different Joints

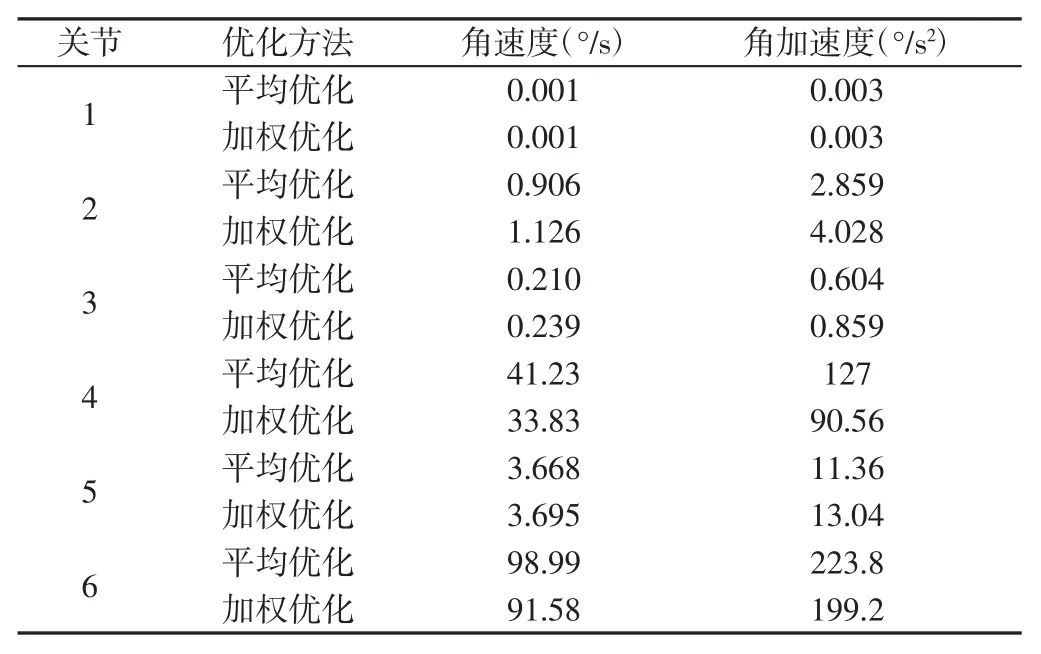
表3 不同优化方法各关节角速度、角加速度最大值Tab.3 Maximum of Angular Velocity and Acceleration of Each Joint in Different Optimization Methods

由图5～图7 和表3 可知，角速度加权优化方法改善了关节轨迹运动参数，如关节4 角速度最大值减少7.4rad/s，角加速度最大值减少36.44rad/s2；关节6 角速度最大值减少7.41rad/s，角加速度最大值减少24.6rad/s2，与此同时，关节2 角速度增加0.22ad/s，角加速度增加1.169rad/s2，关节3 和关节5 角速度和角加速度都少量增加，但变化在合理的安全范围内，相对关节4 和关节6 的明显改善，角速度和角加速度增幅较小。

在规划出的角速度加权优化和平均优化的五次多项式样条上以等时间间隔0.05s 采集各关节角位移数据，可采集到180 组关节角位移数据，通过fkine 函数可求出角速度加权优化和角速度平均优化条件下的末端轨迹，如图8 所示。

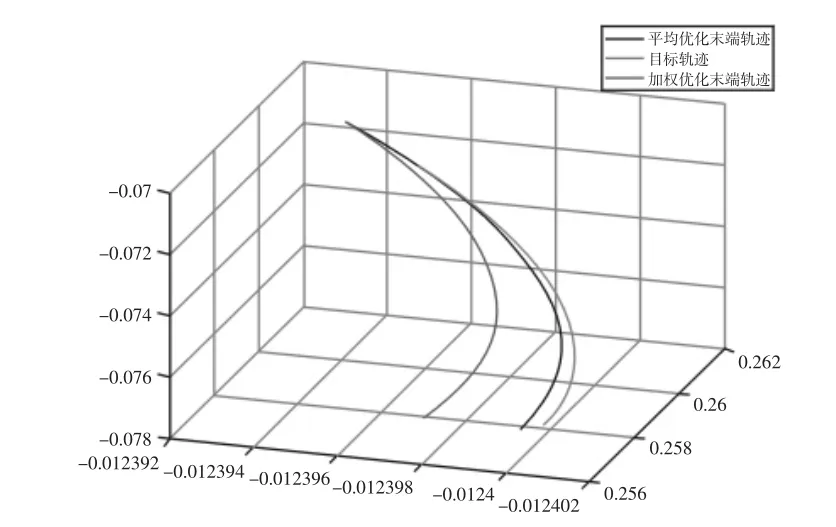
图8 不同优化条件下的末端轨迹图Fig.8 Trajectory in Different Optimization Methods

两种优化方法规划的轨迹在X、Y、Z 方向都有误差，以Z 方向的误差为例进行分析，将规划的轨迹在Z 方向上的摆动做成误差曲线，如图9 所示。

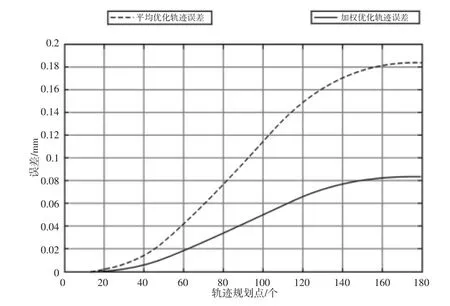
图9 两种优化方法Z 方向上的轨迹误差Fig.9 Trajectory Error in Z Direction in Two Weighted Optimization Method

由图9 可知，基于角速度加权优化的五次多项式规划的轨迹误差相对较小，说明角速度加权优化的五次多项式优于角速度平均优化的五次多项式。

5 结论

以六自由度抛光工业机器人为研究对象，设计基于角速度加权优化的约束条件的五次多项式插值算法。以机器人对手表表壳抛光为例，根据待抛光表面选取的作业关键点进行关节空间轨迹规划，利用逆运动学算法得到各关节在每个路径点的关节角度，经过MATLAB 编程进行仿真验证，该五次多项式插值算法能够较好地满足机器人运动平稳、连续的要求，相比于传统的角速度平均优化的约束条件，具有运动参数变化更小、轨迹误差更小的优点。但结果显示某个别关节角加速度优化后在某个时间段值还是较大的，这也为后续抛光工业机器人轨迹规划的理论研究提供方向。