基于响应曲面的软刚臂结构多目标参数优化

袁 威，董海防，尧白莲，王伟伟

（武汉第二船舶设计研究所，湖北 武汉 430064）

1 引言

软刚臂式单点系泊装置是海洋石油工程领域的关键装备之一，因其具有良好的“风向标效应”被广泛应用于渤海海域FPSO的定位[1]。软刚臂结构是单点系泊装置中连接FPSO 与系泊塔架，为FPSO 提供水平回复力的关键结构件，如图1 所示。

目前，中海油应用于渤海油气开发的六套软刚臂单点系泊装置均由外国公司SOFEC、BLUWATER 等提供，软刚臂结构优化相关文献资料较为缺乏；国内对于软刚臂单点系泊装置的研究也主要集中在单点系泊系统监测技术研究[2]，软刚臂单点系泊系统动力分析等方面[3]，研究成果主要为软刚臂单点系泊系统在线监测、水动力性能计算以及水池实验模拟仿真等方面，具体涉及到结构优化方面的文献较少。

软刚臂结构主尺度主要包括压载重量GY、系泊腿长度LX、压载结构系数k、系泊刚臂长度LR、系泊点高度差△H，任何一个参数的变化都会对水平系泊力产生影响。因此，根据软刚臂结构几何参数及运动特征建立数学模型，以响应曲面分析为基础，结合正交试验设计，将水平系泊力作为设计输入，对软刚臂结构进行多目标参数优化，可以得到最佳结构参数组合。

图1 软刚臂结构实物图Fig.1 Structure of Soft Yoke

2 数学模型分析

2.1 软刚臂结构简化几何模型

软刚臂单点系泊装置结构[4-6]由系泊腿LX、系泊刚臂LR组成，其中系泊腿上端连接FPSO 船艏支架，连接点设为A；系泊刚臂连接系泊塔架轭架铰接头轴承，连接点设为O；系泊腿与系泊刚臂通过万向联轴器进行铰接，连接点设为C，如图1 所示。连接点A、C、O 采用轴承以及万向节等装置进行连接，因此，软刚臂结构对FPSO 的约束为柔性约束，从而降低系泊过程中刚性接触产生的不利影响。

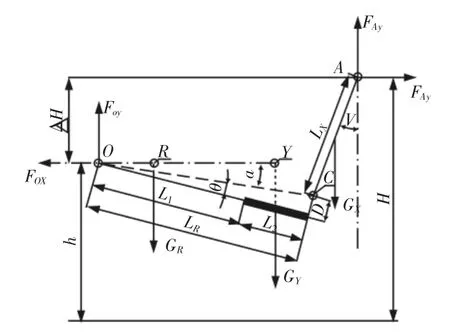
图2 软刚臂结构几何模型Fig.2 Structure of Soft Yoke Geometric Modal

2.2 软刚臂结构工作原理及受力分析

FPSO 在风浪流的作用下，远离或靠近系泊塔架连接点O 时会对结构产生水平方向的系泊力，记为FAX，而连接点A 在软刚臂结构及其重力的作用下，会产生阻碍FPSO 运动的水平回复力，记为水平回复力与水平系泊力大小相等，方向相反。水平系泊力由风浪流与结构耦合作用产生，水平回复力主要由软刚臂结构自重、结构尺寸以及FPSO 水平位移决定。软刚臂结构受力分析，如图1 所示。

根据软刚臂结构受力分析以及软刚臂结构几何模型，推导出水平系泊力FAX计算公式，如式（1）所示。

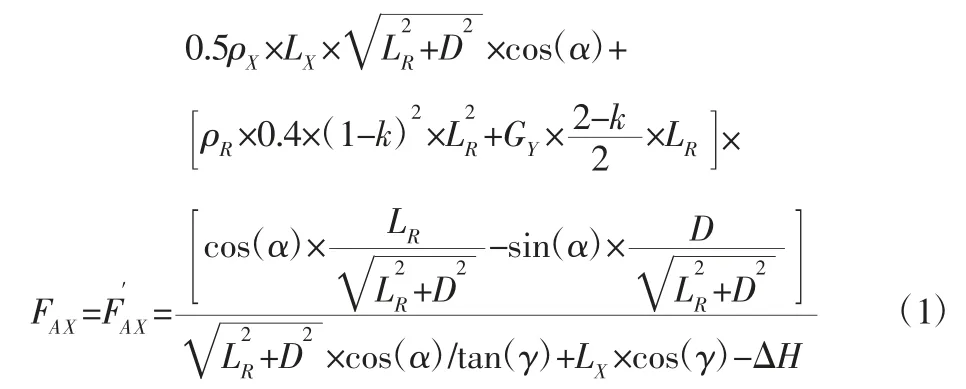
式中：LX—系泊腿长度/m；LR—软刚臂长度/m；D—铰接点 C 距系泊刚臂LR中心线距离/m；GY—压载重量/T；k—压载结构系数；α—平台远离时，OC 与水平方向夹角/rad；γ—系泊腿LX与竖直方向夹角/rad；ΔH—A、C 点高度差/m；ρR—软刚臂连接段线密度（T/m）；ρX—系泊腿线密度（T/m）。

2.3 软刚臂结构水平位移及系统刚度

软刚臂单点结构系统刚度是衡量系泊系统性能优劣的重要指标，良好的系统刚度可以使得FPSO 受到的水平回复力变化平缓，减小外力突变对结构产生的冲击。

软刚臂单点系泊系统水平回复力与水平位移满足胡克定律关系式：

根据图1 简化模型以及软刚臂结构运动特征，绘制FPSO 远离/靠近示意图，如图2 所示，图中A′为平衡位置，此时水平系泊力为0；A 为最大远离状态，A″为极限靠近状态。

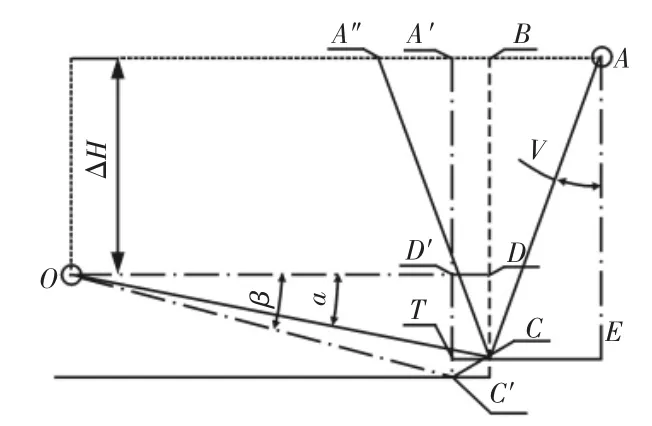
图3 软刚臂结构水平位移Fig.3 Structure of Soft Yoke Horizontal Displacement

根据图2 几何关系，推导出系泊腿LX与竖直方向夹角γ 以及水平位移 ΔX 计算公式，如式（3）、式（4）所示。

3 响应曲面正交优化分析

3.1 优化原理介绍

根据上文所述，软刚臂结构主尺度对单点系泊性能起到决定性作用，同时根据式（1）～式（4）可知，软刚臂结构参数众多，优化设计工作计算量大，因此，寻求一种快速有效的结构参数优化方法可以有效减小设计工作人员的重复计算工作量。

通过以响应曲面分析法为基础[4-7]，结合正交设计优化方法对软刚臂结构主尺度参数进行优化设计。优化原理为：以现有软刚臂结构参数为基础，根据正交设计对各参数进行组合，以水平系泊力为主要响应曲面函数，水平位移为次要响应曲面函数，利用遗传算法进行多目标参数优化，得到最终优化结果。

3.2 优化对象分析

软刚臂结构参数优化主要包括：系泊腿LX、系泊刚臂LR、压载重量GY、压载结构系数k、连接点高度差ΔH。优化目标为在满足系泊系统刚度的前提下，结构尺寸以及重量最小。渤海现役软刚臂单点系泊装置结构参数，如表1 所示。根据平台远离最大位移以及平衡位置与最大远离位置之间的几何关系计算出平衡位置夹角β 以及最大远离夹角α。

表1 软刚臂结构参数Tab.1 Soft Yoke Parameter

3.3 正交设计优化

正交设计是研究多因素多水平的一种设计方法，由于采用正交设计，可以在保证试验精度的前提下大大降低试验次数，减小数据处理工作量，被广泛应多因素多水平试验研究中。软刚臂结构参数众多，且单个参数的变化都会对其它参数产生影响，因此，通过正交设计，选取合适的参数组合，降低结构参数优化计算工作量。结构参数组合，如表2 所示。

表2 结构参数正交组合Tab.2 Orthogonal Combination of Parameters

3.4 优化设计分析

根据正交表格参数组合以及响应曲面函数，利用遗传算法，通过MATLAB 软件编程得到不同参数组合响应曲面，如图所示。由图4（a）～图4（e）可知：软刚臂结构参数直接影响到软刚臂结构所提供的水平回复力大小，具体表现为：随着压载重量GY、系泊腿长度LX的增加，所提供的水平回复力随之增大；反之，随着与压载结构系数k、系泊刚臂长度LR、系泊点高度差ΔH 的增加，所提供的水平回复力随之减小。由图4（f）可知：系泊刚臂长度LR、系泊腿长度LX直接影响到FPSO 远离平衡位置最大距离，允许最大远离距离随着LX的增加而增加，随着LR的增加反而减小。

由此可知，以最大水平系泊力和FPSO 最大远离距离作为设计输入，在响应曲面函数基础上利用遗传算法[8]进行优化，可以得到软刚臂结构参数最优解。优化约束条件为：当FPSO 最大远离平衡位置是，软刚臂结构所能提供的最大水平回复力满足最大水平系泊力要求，优化目标为结构参数最小。最大远离距离ΔX=12m，远离最大系泊力FAX=450（单位/104N）。通过MATLAB 软件多目标遗传算法经过多次迭代优化，得到最终优化结果，如表3所示。

表3 结构参数优化结果Tab.3 Result of Soft Yoke Parameter Optimization

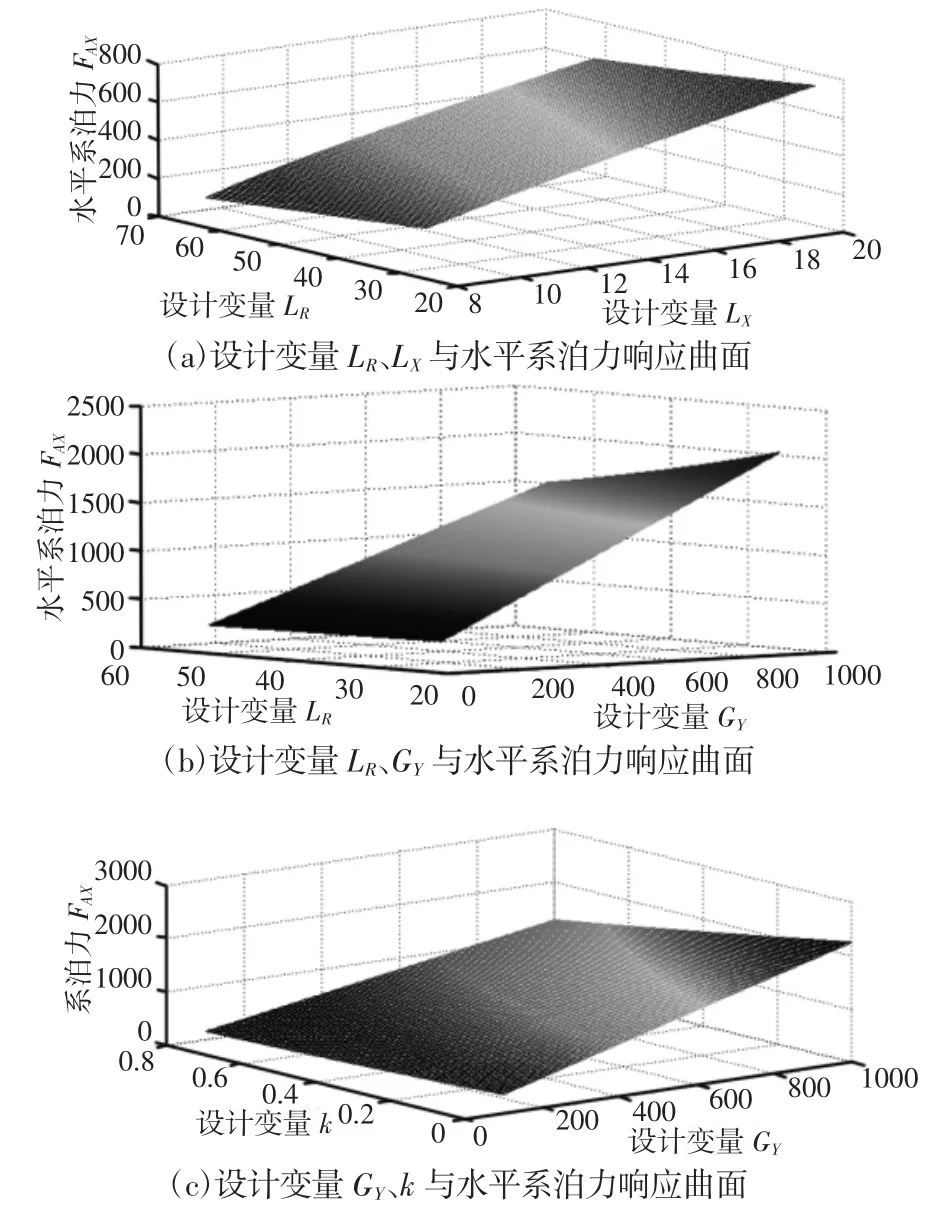
图4 优化参数与优化对象间的响应曲面Fig.4 Response Surface Between Optimized Parameters and Optimized Objects

3.5 优化设计结果分析

根据软刚臂结构参数优化前与优化后的数据进行软刚臂结构刚度分析，得到优化前与优化后刚度曲线，如图5 所示。由图可知，结构参数优化前与优化后系统结构刚度变化趋势一致，系统刚度保持良好。

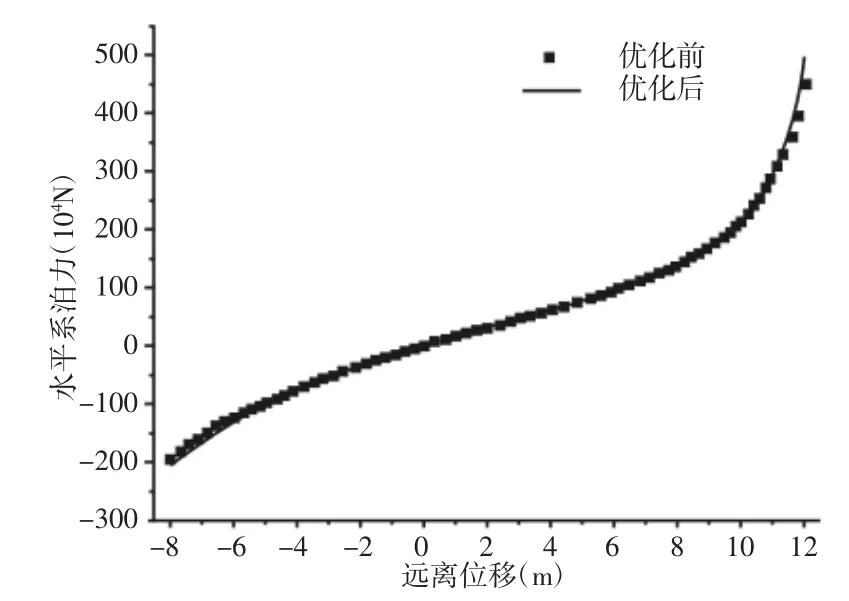
图5 结构参数优化前后系统刚度曲线Fig.5 The Combination of Objective Function and Constraint Function

列举软刚臂结构参数优化前后数值比较，如表4 所示。由表可知，优化后最大靠近位移时所能提供的回复力较之优化前提高4.1%，最大远离位移时所能提供的回复力提高9.66%；优化后压载重量虽然增加1.7%，但是结构整体重量较之优化前减重21.84%；高度差ΔH 优化后增加6.25%，通过降低O 点距离，结构重量将进一步减轻。

表4 软刚臂结构参数优化前后数值比较Tab.4 Comparison of Soft Yoke Parameter Between Before and After Optimization

4 结论

（1）通过建立响应曲面函数，同时结合正交设计方法合理选取参数组合，可以减小计算工作量，提高软刚臂结构参数优化计算效率。（2）优化分析结果表明：随着压载重量GY、系泊腿长度LX的增加，所提供的水平回复力随之增大；反之，随着与压载结构系数k、系泊刚臂长度LR、系泊点高度差ΔH 的增加，所提供的水平回复力随之减小。系泊刚臂长度LR、系泊腿长度LX直接影响到FPSO 远离平衡位置最大距离，允许最大远离距离随着LX的增加而增加，随着LR的增加反而减小。（3）优化后，系统刚度保持良好，同时结构整体重量减小21.84%，减重效果明显。