基于Weisfeiler-Lehman 图核算法的装配体模型比较方法

左 咪，邓 兰，薛 婷，闫起源

（西安建筑科技大学机电学院，陕西 西安 710055）

1 引言

随着三维扫描技术和计算机图形学的发展以及计算机性能的提高，三维模型已成为继声音、图像和视频之后的第四种多媒体数据类型。机械领域的企业经过多年的积累形成了包含丰富经验知识信息的三维模型库，日益发达的互联网技术为人们对三维模型的共享和处理提供了条件，重用这些信息可以大大提高设计生产效率。三维信息相似度比较技术是模型信息检索、通用结构挖掘等三维信息重用的基础。

目前对于三维模型信息比较主要基于：1 三维模型的三维特征提取匹配。但是在三维模型的特征提取过程中，不可避免的会简化部分三维模型的特征，且往往仅从三维模型几何特征出发，进而导致匹配过程的不完全精确。近年来，随着产品全三维体系的不断成熟，CAD 模型在工艺、功能和材料等非几何信息描述方面能力的不断增强，且参与模型定义的设计部门和专业日益增多，进而形成了包含多源信息的CAD 模型[3]因此，基于模型的创建过程进行的三维模型检索从更加全面的角度进行三维装配体模型相似度比较技术可以从结构设计、工艺设计、仿真验证工作和信息表达等多方面支持设计重用。

因此提出基于Weisfeiler-Lehman 图核算法的装配体模型比较方法。首先用图模型对多源装配体模型进行信息的转化表达并进行初步信息归类，形成装配体类码连接图；将W-L 图匹配算法和核函数综合应用，对装配体类码图进行相似度计算，实现装配体之间的相似度计算。

2 装配体类码连接图

装配体模型中包含大量的零件及连接关系，每个零件又包含了外形、尺寸、位置、材料、工艺等多种信息。这些信息的数据类型种类繁杂、量大、存储方式各异，因此，用装配体属性连接图对装配体信息图形化表达，用图中的节点表达装配体中的零件信息，用图中节点之间的连接关系表达零件之间的装配关系。然后分别对节点和连接关系进行分类，用类码简化规整信息表达，形成装配体类码连接图。

【定义 1】装配体属性连接图：G=｛P，E，A（P），A（E）｝，其中，P=｛p1，p2，…，pnp｝表示各个零件节点集合；E=｛e1，e2，…，ene｝表示连接关系集合；A（P）=｛A（p1），A（p2），…，A（pnp）｝表示零件的属性集合；A（E）=｛A（e1），A（e2），…，A（ene）｝表示各个连接关系的属性集合。

为装配体中的零件建立节点属性如下：

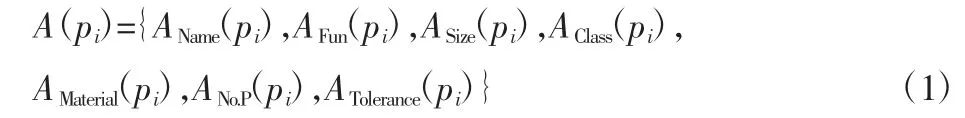
式中：AName（pi）—名称属性；AMaterial（pi）—零件材料；AFun（pi）—零件功能；ASize（pi）—零件尺寸；AClass（pi）—零件类型；由于在机械产品中常常有一些零件成组出现，这些零件且与其他零件具有相同的连接关系，具有相同的功能，我们可以将该组零件用一个节点表达以简化数据；ANo.P（pi）—成组零件节点中的零件个数；ATolerance（pi）—该零件中与零件功能直接相关的最关键的尺寸公差要求，该属性的数据结构为｛公差类型、基本尺寸、偏差值=|上偏差-下偏差|｝，例如轴承内径公差｛尺寸公差、30、0.2｝。零件节点属性可以根据具体应用进行增加或减少。

零件之间的连接关系可以分为普通的接触关系和根据装配工艺文件中有装配要求的连接关系。对于后者可以进一步分类，具体包括螺纹连接、铆接、销钉连接、焊接等。根据连接关系的分类，连接关系的属性建立如下：

式中：AClass（ei）—连接类型；AForm（ei）—连接形式；AMaterial（ei）—连接材料。

具体应用基于密度的DBSCAN 聚类算法分别对零件和连接关系进行聚类，并对相同类型的元素赋予相同的类码。用类码重新定义属性连接图中的节点和连接关系的标签，形成类码连接图。该算法将数据集中高密度区域用低密度区域分割，可以从带有“噪声”的数据集中发现任意形状的聚类，可以有效的进行空间聚类。零件特征信息是由其六类属性定义，因此，由零件属性构成零件属性空间，每个零件可以看作是处于六维空间中的点。将DBSCAN 算法应用于零件属性空间点在零件属性空间中的聚类过程，算法中涉及的点即为零件属性空间点。

DBSCAN 聚类算法过程为：定义在给定半径（Eps）的邻域内数据对象的个数必须大于给定阈值（MinPts）。将DBSCAN 算法应用到零件属性空间，两个点之间的距离与这两个点代表的零件的相似度负相关，即两个零件的相似度越高，它们的点在零件属性空间中的距离越小，反之则越大。因此两个零件点的距离dist（p1，p2）表示如下：

零件和连接关系的相似度计算是比较它们的具体属性值，然后通过加权求和零件各类属性的相似度来确定零件之间的差异。在装配体模型中，由于这些信息的多样性，需要四种不同类型的属性来表示这些信息：（1）标准语义属性，用字符串形式表达。一个零件或连接关系的该类属性的取值是通过从一个已有的列表中选择其中之一来完成，其属性值可以穷举。若两个要比较的属性值相同则相似度为1，否则为0；（2）非标准语义属性，用字符串形式表达。这类属性是在模型定义过程中由参与的设计人员给出，属性值不可穷举。例如一个零件的名称。这类属性用杰卡德（Jaccard）相似度进行比较，即由两个属性中所有字符串的交集和并集的比值确定；（3）量化属性，用具体数值来表达。如一个零件的具体尺寸只能用数值表示。这类属性的相似度为较小值与较大值的比值，两个数值差异越大则相似度越低；（4）公差属性，若公差属性中的公差类型相同且基本尺寸按照（3）中量化属性比较方法相似度高于75%，那么继续用（3）中量化属性比较方法计算偏差值的相似度，否则公差类型不同或者基本尺寸差异较大，公差信息比较无意义，那么在后续的零件相似度比较过程中公差属性相似度不纳入加权比较过程。

3 基于 Weisfeiler-Lehman（WL）图核算法的装配体模型相似度计算

随着图结构的广泛应用，图核算法已经被应用到很多领域并广受关注，成为一个快速发展的结构化数据学习分支。它可以将图形结构化数据和向量机、内核PCA 等大量机器学习算法联系起来，进而解决图结构表示的实际问题。W-L 图核算法将W-L图匹配算法与核函数结合起来，可以有效的进行带标签图结构相似度分析。

3.1 W-L 图匹配算法

1968 年 Weisfeiler 和 Lehman 提出了 k 维 Weisfeiler-Lehman匹配算法，在这里我们应用一维WL 算法，或称单一顶点细分算法，它的基本思路是对每个顶点的所有邻接顶点集合的标签进行排序生成该顶点的邻接点标签序，然后把这个顶点的标签和它的邻接点标签序进行组合压缩再排序形成新的更短的标签，如图2所示。

在W-L 算法的每次迭代中，对于G 和G′中所有节点v，如果在历次迭代中，我们得到的新标签li（p）是一致的，就表明G 和G′具有相同的标签。因为只有在这种情况下，它们才会得到相同的新标签。因此，我们用r（（P，E，li））=（P，E，li+1）表示W-L 算法中的重新定义标签函数。

【定义2】：对G=（P，E，li）=（P，E，l0）进行i 次迭代生成图Gi=（P，E，li）。那么｛G0，G1，…，Gh｝=｛（P，E，l0），（P，E，l1），…，（P，E，lh）｝为W-L 序列图集。

3.2 W-L 图核

用Σi∈Σ 表示在各代W-L 图中各个节点标签集合。用Σ0表示G 和G′的原始节点标签的集合（重复出现的标签在Σi中仅显示一次）。将每个Σi中的元素按照从小到大的顺序排列。用c（jGi，σ）ij表示图G 经过i 次迭代生成图G 中 σij的出现次数。，将图 Gi中的节点信息进行规整压缩，用一个一维向量表达。

对于两个要比较的图生成的一维向量之间，相同标签节点的个数信息一一对应，便于后续的计算比较。如果两个向量方向相同，那么它们的标准内积值最大，如果方向相反，标准内积值最小。因此，内积值的大小可以反应两个向量的相似程度，因此基于向量内积，定义两个图的W-L 图核可以表示为：

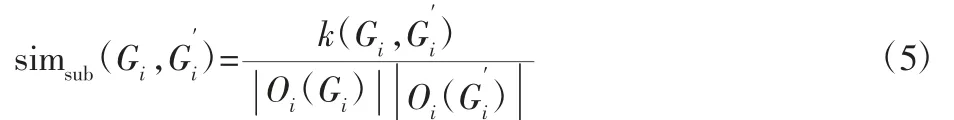
3.3 装配体模型W-L 图核相似度算法

剪枝标注：在每次W-L 算法第i 次迭代之前，我们遍历Gi和中所有节点，标注出来另外一个图节点标签中没有出现过的节点集合及其相关的连接，剩余GWi和如图 2 所示。因为它代表G 和G′中明显相异的部分，后续的W-L 图核算法中仅仅对GWi和迭代，进行标签的重新编排压缩再定义。因此剪枝标注操作可以减小后续W-L 算法中计算图的规模，提高效率。由于Di和代表图 Gi和中相异的部分，所以在计算相似度时用包含Di和的 Gi和来计算。虽然剪枝标注操作可能会导致Gi和分裂成多个子图，但是并不会影响后续的一维向量的转化操作，在这里进行相似度计算的时候，我们仍然可以把它们当作一个整体来计算。

从W-L 图匹配算法中我们可以知道，W-L 算法可以将图中的连接关系信息逐步集成到节点标签信息中，得到W-L 序列图集。那么对于图G 和G′的W-L 序列图集，如果任意一代Di-1和为空，G 和G′图核相似度恒为1，那么迭代结束，说明这两个图同构；如果两个图中有部分子图同构，经过多次迭代之后，相同的子图可能会集中在GWi和中，图核相似度将不会变化成为定值，迭代结束；除了这两种情况外，经过多次迭代，图结构信息将逐步集中到图的节点标签上，直到两个图的标签全部不相同，GWi和为空，相应的图核相似度为0，迭代结束。

那么两个图的相似度根据其W-L 序列图集历代之间的图核相似度计算而得：

4 实例验证

选取一组装配体模型为实例验证对象，这组模型包含2 个减速器模型和2 个飞机卡板模型。先比较2 个减速器模型，经过第一步的装配体信息处理，将模型转化为装配体类码连接图，如图1 所示。

图1 两个减速器模型、属性连接图及其类码图Fig.1 Two Reducer Models，Corresponding Attribute Connection Graphs and Their Class Code Graphs

图2 对减速器模型应用W-L 图核相似度算法第一次迭代Fig.2 Applying First Iteration of W-L Graph Kernel Similarity Algorithm to the Reducer Models

表1 模型1 与模型2 用W-L 图核相似度计算Tab.1 Calculating Similarity Process Between Model 1 and Model 2 by W-L Graph Kernel Similarity Algorithm

图3 两个飞机卡板模型属性连接图及其类码图Fig.3 Two Aircraft Card Board Models，Corresponding Attribute Connection Graphs and Their Class Code Graphs

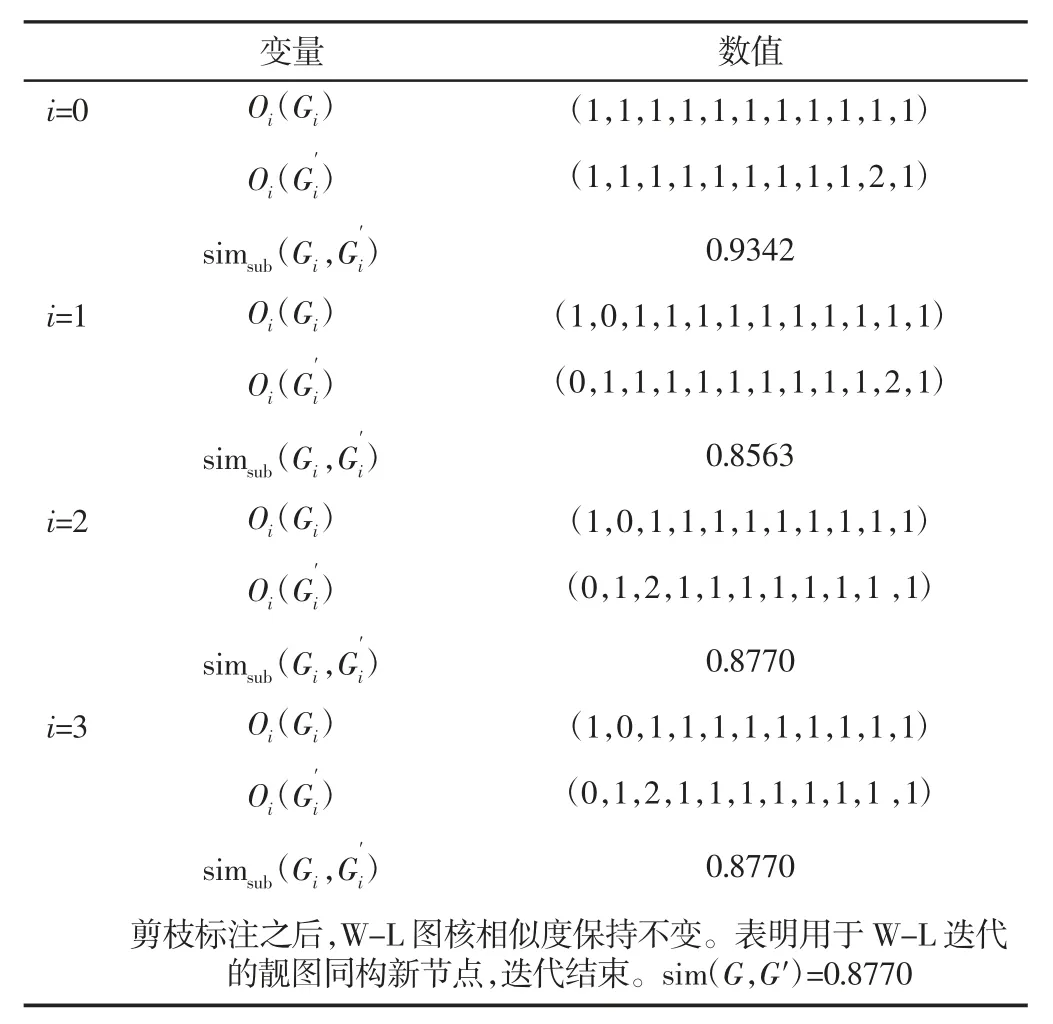
表2 飞机卡板模型用W-L 图核相似度计算Tab.2 Calculating Similarity Process Between Two Aircraft Card Board Models by W-L Graph Kernel Similarity Algorithm

在第一组减速器模型中，模型1 为锥齿轮减速器，模型2 为蜗轮蜗杆传动减速器，但二者都一级减速，用到的轴承、轴承盖、箱体等零件，经过验证计算得到0.7756 的相似度，可以体现其差异和相同的部分。飞机卡板模型中，模型3 和模型4 的包含的零件相同，零件解雇大致相当，但模型4 中多一个角材零件，经过验证计算得到0.9003 的相似度，可以验证算法的有效性。

5 总结与展望

针对多部门参与建立的多源装配体模型的检索、通用结构挖掘等设计重用，建立了一种基于Weisfeiler-Lehman 图核算法的装配体模型比较方法。

（1）装配体类码连接图可以将复杂纷乱的多源装配体信息整理成图模型，便于成熟的图论算法应用，类码可以将部分信息复杂的属性信息进行初步比较分析并简化成便于数学运算的数字形式，降低图信息的复杂度。

（2）W-L 算法融合核函数不用计算复杂的非线性变换，直接得到非线性变换的内积，应用于图的模型中可以大大简化计算复杂度，实现图之间的相似度计算进而实现装配体之间的相似度计算。

在相似度分析过程中没有将图中的连接关系的标签信息、零件之间的装配体尺寸公差等要求纳入比较过程，在后续研究中可以进一步完善；另外装配体的比较过程中，没有体现不同零件之间在比较过程中的差异性还需后续进一步研究。