螺栓的转角法预紧仿真研究

2020-11-23阳光武肖守讷

机械设计与制造 2020年11期

柯新，阳光武，朱涛，肖守讷

（西南交通大学牵引动力国家重点实验室，四川成都 610031）

1 引言

螺栓连接是最常见的机械连接之一，被连接件接触面贴合的紧密程度和预紧程度是保证连接可靠的关键。拧紧螺栓可使螺栓获得一定的预紧载荷，预紧载荷既要使螺栓连接的质量满足要求，也要使螺栓的强度满足要求。因此，仿真过程中准确地模拟螺栓预紧，对于分析含螺栓结构的可靠性问题具有重要意义。

采用ANSYS 软件进行有限元仿真分析时，螺栓预紧载荷的施加方法主要有以下3 种：

（1）预紧单元法：在螺栓杆截面创建预紧单元PRETS179，用SLOAD 命令或在Pretension Section Load 模块施加载荷。

（2）渗透接触法：在Contact Manager 模块中定义螺栓头支承面与被连接件的过盈接触关系。

（3）降温法：对螺栓杆定义温度场，当温度降低时，螺栓杆收缩产生轴向位移实现预紧。

文献[1]提出采用预紧单元法模拟螺栓预紧的结果比降温法和渗透接触法更准确。文献[2]提出采用预紧单元法计算结构的应力能得到足够的计算精度。文献[3]提出降温法预紧适用于所有复杂紧螺栓连接结构。文献[4]提出预紧单元法不适合受剪螺栓的预紧模拟，而降温法和渗透接触法则可用于受剪螺栓的预紧模拟且结果相近。

实际上，由于螺栓在预紧过程中始终受到拉力和扭矩的共同作用，所以螺栓杆和螺纹表面始终处于复杂的多轴应力状态。然而，上述3 种预紧载荷的施加方法均不能准确模拟出螺栓在预紧过程受到的拉扭复合应力的作用。基于ANSYS 软件，采用固定螺母，并在螺栓头施加一定转角的方法，真实地模拟了螺栓的预紧过程，为准确研究螺栓杆受力、螺纹表面应力应变分布提供了一定借鉴意义。

2 螺栓预紧过程的受力分析

假设某点的应力张量为：

由第四强度理论，定义等效应力σe为：

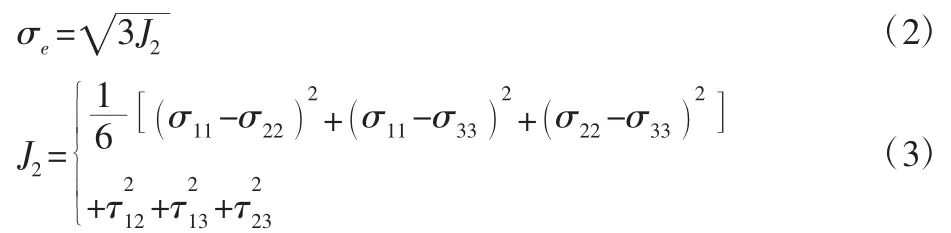
式中：J2—应力偏张量的第二不变量。

由于螺栓在预紧过程中，螺栓杆和螺纹表面始终受多轴应力作用，根据式（2）、式（3），螺栓无螺纹杆上的拉扭复合等效应力σeB[5]为：

式中：σz—轴向拉应力；τt—切应力；FM—螺栓预紧载荷；d—螺栓无螺纹杆段直径；d2—螺纹中径；α—螺纹牙型角半角；MG—螺纹力矩；WP—扭转截面系数；P—螺距；μG—螺纹副摩擦系数。

3 螺栓的预紧仿真

3.1 螺栓连接结构的三维模型

根据 GB/T 1228-20060[6]、GB/T 1229-2006[7]确定 M12 X50 大六角头螺栓、螺母的相关尺寸参数，如图1、图2、表1 所示。

图1 螺栓结构示意图Fig.1 Schematic Diagram of Bolt Structure图中：ls—无螺纹杆长度；lk—夹紧长度。

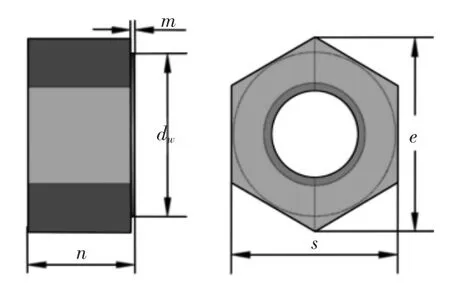
图2 螺母结构示意图Fig.2 Schematic Diagram of Nut Structure

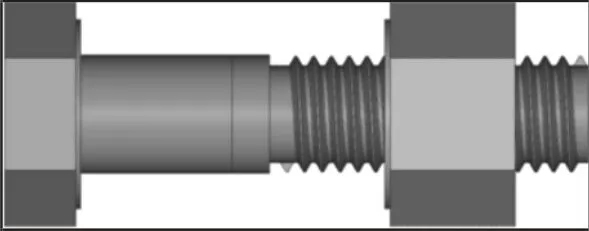
图3 螺栓与螺母旋合示意图Fig.3 Schematic Diagram of Screw of Bolt and Nut

表1 螺栓尺寸参数（单位：mm）Tab.1 Size Parameters of Bolted Joints Structure

螺栓杆上设有16.5 圈螺纹，为避免螺栓与螺母发生螺纹滑脱现象，螺栓杆下部螺纹比螺母多3 个螺距。初拧落座状态下，螺栓杆上部螺纹比螺母多5 个螺距，这样一方面可避免无螺纹杆截面突变对螺栓、螺母旋合工作螺纹应力应变仿真结果的影响，另一方面可保证复拧和终拧时，螺栓或螺母可进一步沿螺旋升角相对运动，螺栓与螺母旋合图，如图3 所示。

螺栓与螺母螺纹均为右旋单线普通三角螺纹，且均未设置引导螺纹和收尾螺纹，三角螺纹的原始三角形高为P。根据GB/T 197-2003[8]，在原始三角形的基础上取外螺纹牙底、内螺纹牙顶的削平高度为H′/4，外螺纹牙顶、内螺纹牙底的削平高度为H′/8，由此得到的基本牙型，如图4 所示。取螺栓与螺母上内、外螺纹的公差带位置为6H/6h。外螺纹大径公差为Td/2，Td=0.265mm；内螺纹小径公差TD1/2，TD1=0.335mm，如图5 所示。设置大、小径公差是为了使内外螺纹可在径向发生相对运动，避免发生内、外螺纹胶合、咬死现象。

图4 原始三角形和基本牙型Fig.4 Primitive Triangles and Basic Teeth图中：a—原始三角形；b—中径线；c—基本牙形。

图5 内、外螺纹配合图Fig.5 Internal and External Thread Matching Diagram

螺栓连接结构，如图6 所示。两被连接件均为厚15mm 的钢板，钢板外径为60mm。根据JGJ82-2011[9]，板上螺栓孔直径为13.5mm，装配完成后无螺纹杆与被连接件的间隙为0.75mm。

图6 被连接件结构示意图Fig.6 Schematic Diagram of the Connected Members

3.2 螺栓连接结构的有限元模型

螺栓连接结构的有限元模型采用SOLID185 单元离散，为了保证计算精度，除螺纹杆中心R=1.5mm 圆柱段与螺母六角面用四面体单元外，其余均采用六面体单元，整个有限元模型共有3326024 个单元和2971201 个节点。螺栓与螺母有限元模型，如图7 所示。在ANSYS 的Contact Manager 模块中定义了5 组的面-面接触对：螺栓头/上部被连接件（Contact Ι）、上部被连接件/下部被连接件（Contact ΙΙ）、螺栓杆/被连接件螺栓孔壁（Contact ΙΙΙ）、下部被连接件/螺母（Contact ΙV）、螺栓螺纹/螺母螺纹（Contact V）。目标单元为TARGE170，接触单元为CONTA174，接触行为为Standard 法向单向接触，接触探测点为Guass 积分点，接触算法为增广拉格朗日算法，允许ANSYS 自动更新接触刚度，如图8所示。除ContactΙΙΙ 外，忽略接触对的初始间隙和穿透，即建立“刚好接触对”[10]。ContactΙΙ 的摩擦系数为 0.23，其余接触对的摩擦系数均为0.12。ContactΙΙΙ 可用于研究螺栓杆与被连接件孔壁接触后的承压情况。为方便提取螺栓头转动一定角度后产生的预紧载荷FM，在螺栓无螺纹杆段设置的提取预紧载荷的节点组，如图9 所示。由于实体单元没有转动自由度，因此，在螺栓头部设定1 个MASS21 单元作为参考点，用rigids 将螺栓头部的节点耦合到该参考点上，由此可将参考点的转动刚性地等效传递到从节点上，最终实现螺栓头的转动。模型的边界条件为：螺栓头—仅给MASS21 参考点提供0.25rad 绕螺栓轴线转动的强迫转角；螺母—全约束；被连接件—仅释放沿螺栓轴向的平动自由度。为方便观察计算结果，为整个有限元模型定义了局部柱坐标系，如图10 所示。

图7 螺栓与螺母有限元模型Fig.7 Finite Element Model of Bolt and Nut

图8 接触对示意图Fig.8 Contact Pairs

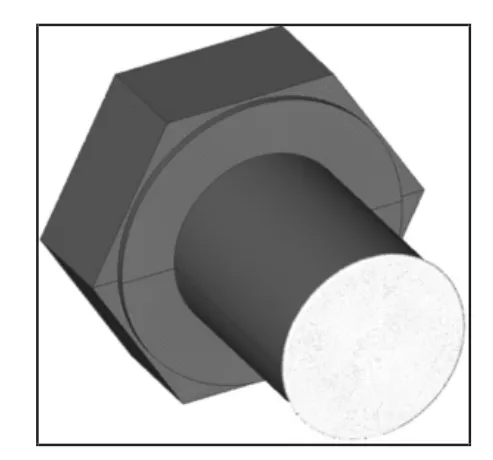
图9 提取预紧载荷的节点组Fig.9 Node Group for Extracting Preload

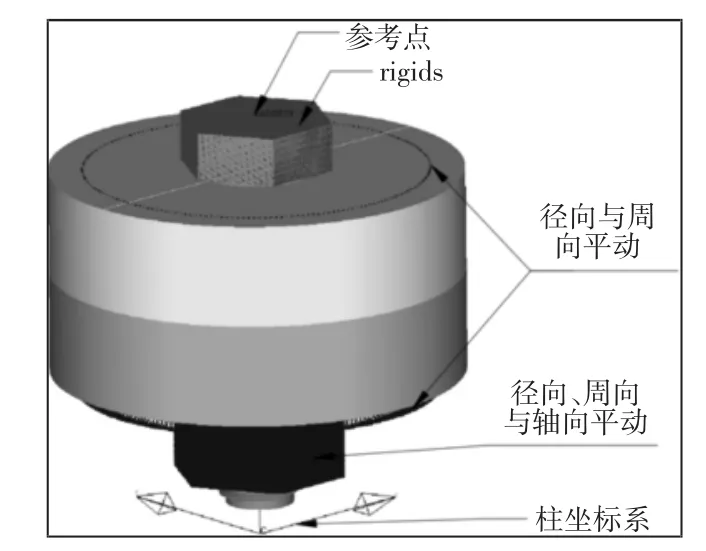
图10 约束、边界条件和柱坐标示意图Fig.10 Constraints，Boundary Conditions，and Cylindrical Coordinates

由文献[11]可知：螺栓各螺纹受载不均，第1 圈工作螺纹承载最大，通常还伴随发生塑性变形。因此，将螺栓、螺母的材料模型设置为双线性随动弹塑性材料模型，屈服强度为460MPa，抗拉强度为620MPa。

3.3 螺栓预紧的有限元结果分析

3.3.1 转角法

基于上述有限元模型进行仿真计算。计算完成后，从ANSYS后处理模块中提取0.25rad 转角产生的预紧载荷为FM=13224N。因此，根据式（4）～式（7），螺栓无螺纹杆段预紧载荷截面上的理论应力为：

σz=116.926MPa；τt=40.197MPa；σeB=136.085MPa

螺栓无螺纹杆段提取预紧载荷截面上的轴向拉应力、扭转切应力和Von Mises 等效应力云图，如图11 所示。对所有计算节点的应力值取平均可得：截面平均轴向拉应力为120.362MPa、截面外圆周平均扭转切应力为40.298MPa、截面平均Von Mises 等效应力为137.568MPa，有限元仿真应力与理论应力值的误差绝对值，如表2 所示。由表2 可知：采用转角法预紧时，螺栓无螺纹杆段轴向拉应力、扭转切应力和拉扭复合等效应力的有限元仿真计算结果与理论值的误差均在3%以内，说明转角法预紧具有较高的准确性，能够较为准确模拟出螺栓在预紧过程中受到的拉扭复合应力的作用。

表2 转角法仿真应力与理论应力的误差绝对值Tab.2 Absolute Value of Error between Simulated Stress and Theoretical Stress by Rotation Angle Method

图11 螺栓无螺纹杆段预紧载荷截面应力云图Fig.11 Cross Section Stress Cloud Diagram of Pretensioning of Bolt by Rotation Angle Method

图12～图13 为螺栓螺纹杆段的Von Mises 等效应力、塑性应变云图。由图可知：前3 圈工作螺纹牙牙底的应力较大，其中第1 圈工作螺纹牙受载最大，与实际情况一致。第1 圈工作螺纹牙牙底的Von Mises 等效应力为460.452MPa，与材料的屈服强度（460MPa）近似相等，说明此处发生了局部塑性变形。若螺栓连接结构上作用有幅值较大的交变动载荷时，螺栓可能在此处发生疲劳断裂。

图12 螺纹杆的Von Mises 等效应力云图Fig.12 Von Mises Equivalent Stress Cloud Diagram of Threaded Rod

图13 螺纹杆的Von Mises 塑性应变云图Fig.13 Von Mises Plastic Strain Cloud Map of Threaded Rod

3.3.2 预紧单元法

在目前常用的螺栓预紧仿真方法中，普遍认为：如果单纯地进行预紧仿真，采用只有螺栓轴向自由度的预紧单元法模拟具有较高的准确性。因此，为了对比转角法与预紧单元法在模拟螺栓预紧时，仿真结果精确度的高低，取相同的螺栓连接结构，再用预紧单元法进行螺栓的预紧仿真。

在提取预紧载荷的截面上设置PRETS179 单元，并施加FM=13224N 预紧载荷。模型的边界条件为：螺栓头、螺母—自由无约束；被连接件—全约束。PRETS179 单元、边界条件和局部柱坐标，如图14 所示。仿真计算完成后，螺栓无螺纹杆段提取预紧载荷截面上的轴向拉应力、扭转切应力和Von Mises 等效应力云图，如图15 所示。

图14 PRETS179 单元与边界条件示意图Fig.14 Schematic Diagram of PRETS179 and Boundary Condition

对所有计算节点的应力值取平均可得：截面平均轴向拉应力为120.313MPa、截面外圆周平均扭转切应力为1.091MPa 和截面平均Von Mises 等效应力为127.653MPa，有限元仿真应力与理论应力的误差绝对值，如表3 所示。

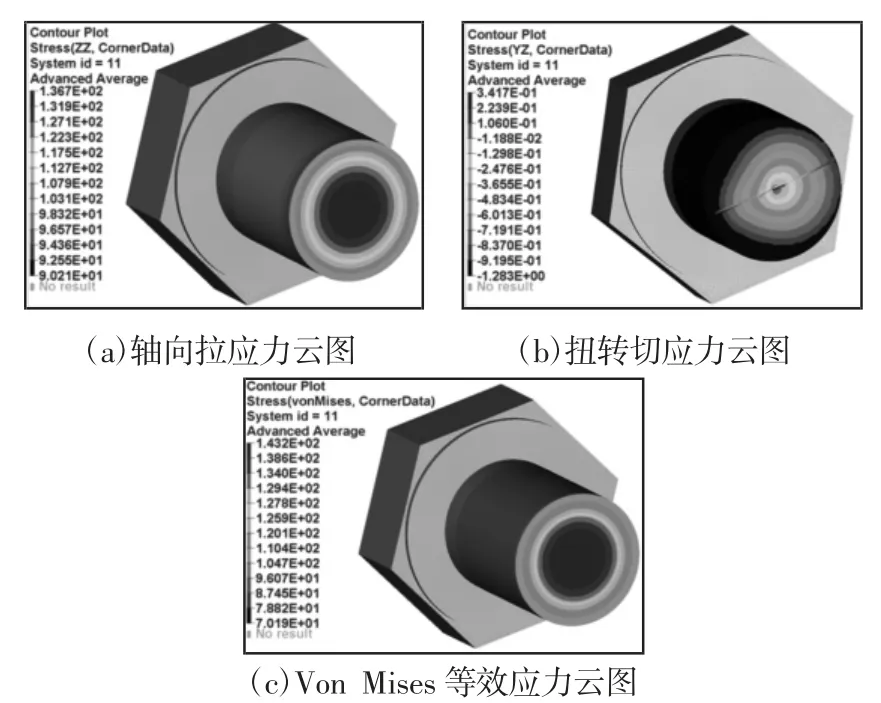
图15 螺栓无螺纹杆段预紧载荷截面应力云图Fig.15 Cross Section Stress Cloud Diagram of Pretensioning of Bolt by Pretension Element Method

表3 预紧单元法仿真应力与理论应力的误差绝对值Tab.3 Absolute Value of Error between Simulation Stress and Theoretical Stress by Pretension Element Method

由表3 可知：采用预紧单元法预紧时，螺栓杆上的拉应力仿真结果与理论值相符，但却几乎不产生扭转切应力，说明预紧单元法不能准确模拟螺栓在预紧过程中受到的拉扭复合应力作用的状态。

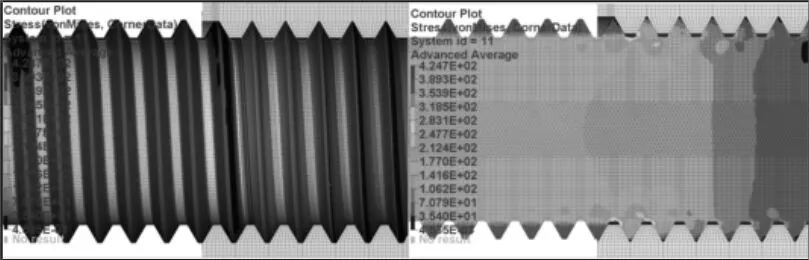
图16 螺纹杆的Von Mises 等效应力云图Fig.16 Von Mises Equivalent Stress Cloud Diagram of Threaded Rod

螺栓螺纹杆段的Von Mises 等效应力云图，如图16 所示。由图可知：前3 圈工作螺纹牙牙底的应力较大，其中第1 圈工作螺纹牙受载最大，与转角法预紧情况相同。第1 圈工作螺纹牙牙底的Von Mises 等效应力为424.702MPa，小于材料的屈服强度（460MPa），未发生塑性变形。

转角法的结果显示螺纹杆第1 圈工作螺纹牙底处发生了局部塑性变形，而预紧单元法却得出了相反的结论。这是由于：预紧单元法无法计入扭转切应力的影响，使仿真的应力结果总体偏小，导致得到的应力应变结果偏于保守，不利于螺纹表面应力应变的研究分析。

与起始内螺纹旋合的外螺纹的Von Mises 等效应力云图，如图17 所示。由图17 可以看出：预紧单元法在该处会发生螺纹副间的挤压现象，使外螺纹在挤压处发生较大的变形，而转角法不存在这一现象。说明采用转角法预紧时，螺纹副会依照螺旋升角旋合实现预紧。而采用预紧单元法预紧时，由于PRETS179 单元只能提供单纯的轴向预紧载荷，使螺纹副发生轴向挤压变形，却不能模拟出螺纹副间的旋合过程，因此，预紧单元法不可用于准确分析螺纹表面的应变情况。