作动器故障对阵风减缓系统的影响研究

杨建忠，李 勇，杨士斌，王立宝

（中国民航大学适航学院天津市民用航空器适航与维修重点实验室，天津 300300）

1 引言

现代大型客机的设计普遍采用轻型材料来减轻机翼结构重量并增大展弦比以提高飞机的经济性。然而，随之带来的问题是机翼结构弹性增大导致一系列不利的气动弹性影响。近四十年来的热门研究方向是通过主动控制技术来降低气动弹性带来的不利影响，例如颤振抑制和阵风减缓[1]。但是采用了主动控制技术后，在气动弹性问题中必须要考虑“伺服”的影响，即气动伺服弹性（ASE）[2]。操纵面作为飞机飞行控制系统中重要的部件负责按照飞控计算机的控制指令进行运动从而控制飞机在空中改变姿态。根据NASA 对民用飞机1988 年至2003 年失控事件/事故原因的分析报告[3]，操纵面故障引起的事故8 起、事件144 起，操纵面故障一般是由液压系统失效、作动器失效或结构损伤引起。此外，对于电传飞控（FBW）的飞机，电传飞控系统失效会导致操纵面非指令性振荡，这会与气动弹性强烈耦合导致产生极大不利载荷或振动[4]。为了解决这一问题，过去二十年间大量学者就容错飞行控制进行了研究[5]，其中绝大多数研究中的飞机动力学模型仅考虑飞机刚体模型，忽略弹性效应，研究用于恢复或保持飞机刚体运动的控制律算法。然而，在飞行过程中，传感器在探测飞机刚体运动的同时也会受到飞机弹性模态的影响。文献[6]分析了几种典型主操纵面卡阻对弹性飞机的影响，其故障类型为操纵面分别卡阻在1°、3°和5°。此外，在气动伺服弹性问题研究中，作动器模型一般以传递函数简化表示，无法表示各种作动器故障模型。

对于作动器容错控制也有大量研究[7-10]，但是这方面研究更多关注的是作动器本身的建模及设计，一般不考虑气动力载荷或气动力为给定值。为了研究作动器故障对气动伺服弹性带来的影响，通过MATLAB/SIMULINK 平台建立了含操纵面的二元机翼气动弹性模型，通过AMESim 软件建立了高精度非线性电静液作动器（EHA）模型，利用两个软件的联合仿真技术研究了EHA 典型故障对弹性机翼阵风减缓系统的影响，提出了一种阵风减缓系统故障仿真方法。

2 气动弹性建模

这里研究的弹性机翼采用经典无后掠/无尖削简单机翼模型[11]，机翼展长为s、弦长为c、根部有两个旋转弹簧提供扑动κ 和俯仰θ 两个自由度，如图1 所示。弹簧位于弹性轴末端，刚度分别为Kκ和Kθ，弹性轴位于气动中心（1/4 弦长）后方ec 处。假定机翼具有等质量分布。舵面弦长为Ec，舵面偏角为β。

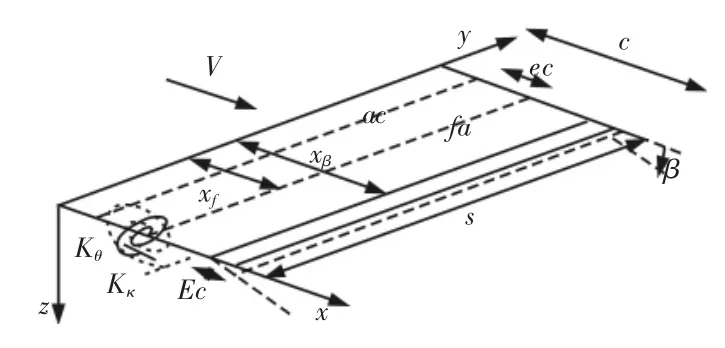
图1 二元气弹模型Fig.1 Binary Aeroelastic Model

机翼上某点的位移（取向下为正）为：

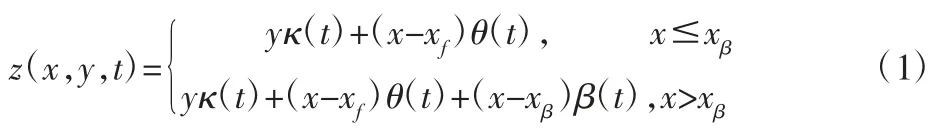
其中动力运动产生的动能为：

机翼俯仰和扑动势能为：

翼面上气动力和气动力矩所做的增量功为：

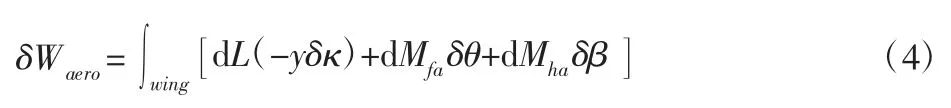
式中：Mfa、Mha—绕弹性轴和铰链线的气动力矩。

铰链力矩所做的增量功为：

式中：Mβ—铰链力矩。

根据Lagrange 能量方程

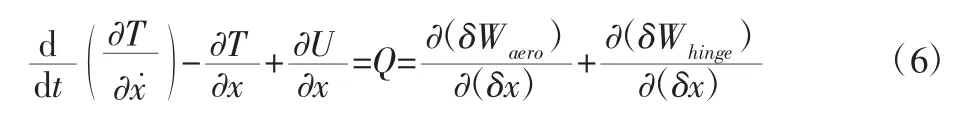
得到带操纵面二元机翼气弹方程

翼尖前缘竖直方向的位移为：

将输出量-Mβ和ztip写成状态空间形式为：

离散阵风模型是用来代表单一离散最大湍流情况，离散阵风的形状为1-cosine（即versine 函数），数学模型为：

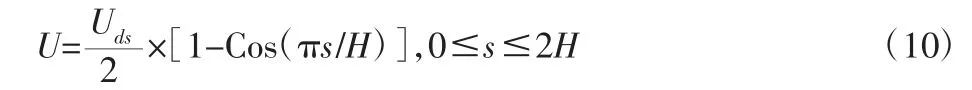
式中：s—进入阵风区的距离（米，英尺）；Uds—设计突风速度；H—阵风梯度（米，英尺）。

3 EHA 建模

电静液作动器是现代功率电传飞机（PBW）中广泛使用的机载作动器。典型电静液作动器由控制器、永磁直流电机、柱塞泵、储能器、单向阀、安全阀、模式选择器、位置和速度传感器、作动筒组成。控制器接受控制信号以及各种反馈信号，生成永磁直流电机的控制电压。电机带动双向定量柱塞泵旋转，输出高压油到作动筒完成对铰链的驱动。

采用AMESim 多学科领域复杂系统建模仿真平台进行EHA的数学建模。AMESim 可以使用户从繁琐的数学建模中解放出来从而专注于物理系统本身的设计。在进行建模时，用户可以从所有模型中提取出的构成工程系统的最小单元使得用户可以在模型中描述所有系统和零部件的功能，而不需要书写任何程序代码。库中的模型和子模型是基于物理现象的数学解析表达式，所有的这些来自不同物理领域的模型都是经过严格的测试和实验验证的。

3.1 永磁直流电机建模

永磁直流电机模型用来计算电机的输出转矩和输出转角，如图1 所示。

图2 永磁直流电机Fig.2 Permanent Magnet DC Motor Model

电机电枢电流和输入电压的关系为：

反电动势为：

式中：Ia—电枢电流；U—输入电压；E—反电动势；Δu—电压损耗为10%；R—电枢电阻，取为0.6Ohm；Ke—反电动势常数，取1.8；ω—电机转速。

电机产生转矩与通过绕组的电流成正比，则电机产生的转矩为：

由于电机和液压泵直接相连，施加在泵上的转矩负载直接由电机驱动，因而可得转矩方程为：

式中：T—电机输出转矩；KT—电机磁力矩系数；JM—电机转动惯量；B—阻尼系数；TL—负载转矩。

3.2 液压系统建模

液压系统包括液压泵、单向阀、储能器、模式选择阀、安全阀和作动筒。其中液压泵模型根据电机的输出转速计算泵排量。采用双室双杆液压缸模型将液压油流量转化为活塞的一维直线运动。

液压泵的瞬时位移为：

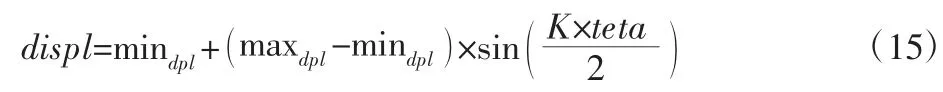
流量方程：

参考压力为进出口压力的线性组合：

系数fact 由转速方程计算：

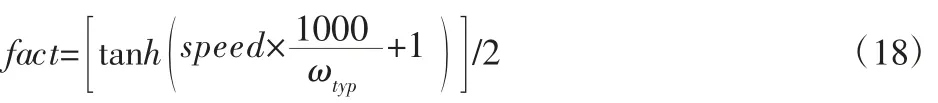
式中：ωtyp—典型液压泵的速度；maxdpl—最大泵位移；mindpl—最小泵位移；teta—液压泵角位移；speed—液压泵转轴速度；K—多轴频率脉动；系数 fact 在（0～1）之间变化，以确保+ωtyp/100到-ωtyp/100 平稳变化。

采用理想液压泵模型，其中，ωtyp取 1000rev/min；maxdpl取110cc/rev；mindpl取 100cc/rev；K 取 6。

4 机翼-作动器耦合气弹模型

EHA 在铰链前的操纵力矩为Mhinge，由舵面气动弹性产生的铰链力矩为Mβ，舵面/铰链转动角度为β，则铰链的动力学方程为：

式中：Jhinge—绕铰链线的转动惯量；ffriction—摩擦力矩系数。

联立式（7）、式（9）、式（10）、式（20）即可得到由 EHA 驱动的机翼气动弹性阵风响应方程。

通过AMESim 和MATLAB simulink 联合仿真方法，对机翼气动弹性模型和EHA 仿真模型进行联合仿真。在simulink 模型中加入PID 控制，具体仿真框图，如图4 所示。

图3 联合仿真框图Fig.3 Block Diagram of the Co-Simulation Model

5 EHA 故障对机翼阵风减缓系统的影响

5.1 阵风减缓系统正常工作状态

算例的二元机翼展长s=8、弦长c=1、气动中心在1/4 弦长，质心距前缘位置xc=0.5c、弹性轴距前缘位置xf=0.48c、升力线斜率 aw=2π、单位面积质量 m＝5、气动阻尼项动和俯仰频率分别为4Hz 和8Hz，操纵面弦长为0.25c，舵面最大偏转位置为30°。通过特征值法求得机翼的颤振速度VF为17.4m/s。机翼在0.8VF下遭遇2m/s 的1-cos 型阵风的开闭环响应，如图5所示。从图中可以看出，该阵风减缓系统对1-cos 阵风的减缓效果为28.9%。

图4 机翼在0.8VF 下遭遇1-cos 阵风的时域响应Fig.4 The Time-Domain Response of Wing in the 0.8VF Under 1-Cos Gust

5.2 EHA 故障

通常EHA 故障类型为电气故障和液压系统故障[12]。电气故障分为电动机故障、控制器故障和传感器故障，液压系统故障分为柱塞泵故障、阀故障和作动筒故障。以舵偏位置传感器故障为例，研究EHA 故障对机翼阵风减缓系统的影响，其他故障类型研究方法与此类似。传感器故障可分为传感器功能丧失和异常。传感器功能丧失指传感器信号断路，功能异常指传感器输出信号与正常信号发生偏差，通常可以归纳为信号卡死、变增益和恒偏差。令yin为传感器正常时的输入值，yout为传感器失效时的输出值，则传感器信号卡死的失效模型为：

式中：α—常数。

传感器恒变增益的失效模型为：

式中：β—恒增益变化的比例系数。

传感器恒偏差失效的失效模式为：

式中：Δ—恒增益变化的比例系数。

5.3 EHA 故障对阵风减缓系统影响分析

5.3.1 舵偏传感器功能丧失

当传感器信号断路时，表现为输出信号为0。系统时域响应，如图6 所示。当舵偏传感器功能丧失时，EHA 闭环系统没有反馈舵偏位置信号，EHA 无法准确控制作动器按照指令信号进行运动。从响应曲线中可以看出，虽然对于最大机翼位移，系统减缓效果从28.9%增加到了62.1%，但是翼尖出现反向位移，并且在2.4s之后舵面和机翼产生了3.2Hz 的极限环运动，这会引起机翼结构疲劳问题。

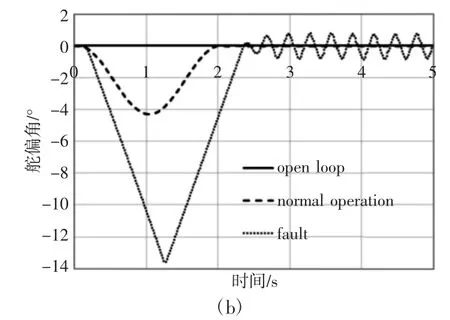
图5 舵偏传感器功能丧失时系统时域响应Fig.5 The Time-Domain Response Under the Sensor Funcion is Lost

5.3.2 舵偏传感器功能异常

根据式（21）～式（23）模拟舵偏传感器的卡死（ss）、变增益（sg）和恒偏差（sd）故障，传感器输出范围为（-30～30）°。系统时域响应，如图6～图8 所示。

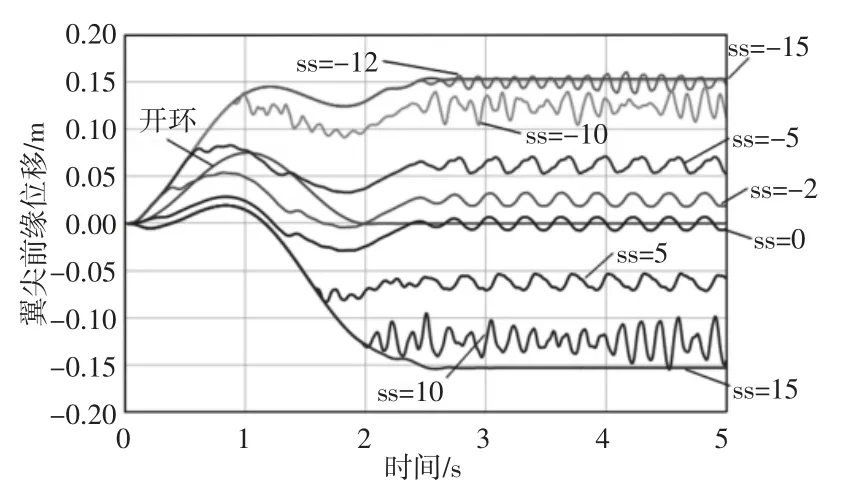
图6 舵偏传感器卡死失效时系统时域响应Fig.6 System Time-Domain Response Under the Rudder Sensor is Jam

当传感器输出信号卡死在某一值（ss）时，阵风减缓系统功能出现异常。输出信号时，系统依然具有阵风减缓效果，且阵风过去后，系统出现极限环振荡。当输出信号时，系统响应最大值大于开环响应最大值，失去阵风减缓效果；且随着信号绝对值增大，阵风过去后机翼前缘位移由极限环振荡逐渐转变为不规则周期性振荡，频率加快，振幅增加；当信号继续增大，周期性特征消失。当输出信号时，不规则振荡逐渐减弱，变为极限环振荡，最终位移保持在0.153m（-0.153m），此时舵面偏角恒为-30°（30°）。

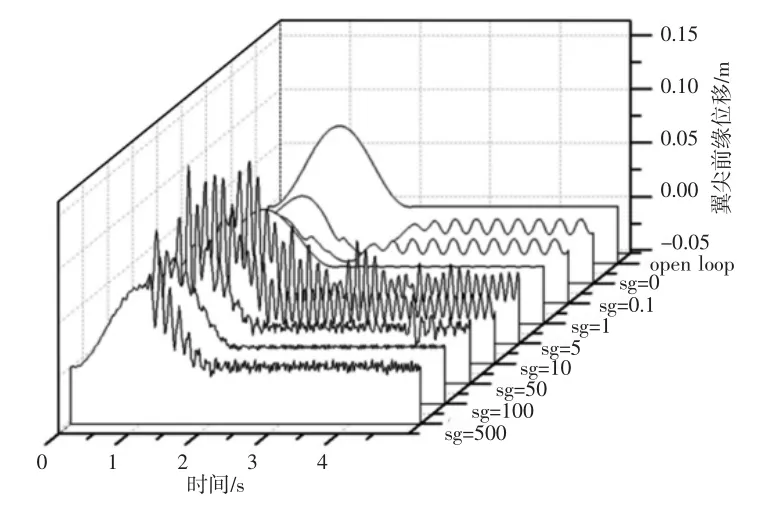
图7 舵偏传感器变增益时系统时域响应Fig.7 Time-Domain Response of the Gain of the Sensor is Changed

传感器中放大电路一般采用二极管实现，当二极管发生失效时，增益变化范围为［0，a），a 为放大电路物理特性决定的最大增益。这里假设传感器正常工作时增益为1，a 为无穷大，根据仿真结果，当增益变化sg＜1 时，系统具有阵风减缓效果，但阵风过去后发生极限环振荡。当增益变化1＜sg＜100，系统失去阵风减缓功能，且发生不规则振荡，系统振荡幅值随增益变化增加先增加后减小，频率逐渐增加；当sg＞100 时，系统振荡幅值逐渐增加，最终逐渐稳定在振幅为0.01m 的不规则周期性振荡，系统最大响应稳定在0.1232m。

图8 舵偏传感器恒偏差失效时系统时域响应Fig.8 Time-Domain Response of the Constant Deviation Fails of the Sensor

恒偏差可以看做是系统中产生恒值错误信号。系统在恒偏差失效状态下最终都会产生非指令性振荡，随着偏差值的增大，振荡振幅先增大后减小，频率逐渐增大，振荡呈现由周期性到非周期性的变化。

6 结论

利用AMESim 和MATLAB Simulink 联合仿真技术，建立了EHA 作动的二元机翼阵风减缓系统仿真模型，给出了EHA 故障对阵风减缓系统响应影响的研究方法。基于该模型，研究了EHA舵偏传感器功能丧失和异常情况下对阵风减缓系统的影响，在这些故障情况下，系统在一定失效范围内仍有减缓效果，但会会产生极限环振荡；超出该范围，系统的振荡幅值以及振荡频率都将改变，系统产生非周期性不规则振荡或周期性不规则振荡。