以小儿盐酸麻黄碱滴鼻液为例探索用R 语言预测儿童用药需求

田 刚

（天津市儿童医院，天津 300134）

药品生产管理者在制定生产计划时要以销定产，为此，要根据以往市场需求量来预测未来市场需求量，但单纯依靠经验预测未来需求量的做法存在一定局限性。这是医院制剂室和药厂普遍遇到的问题。为获得精准的预测，传统上一般根据管理经济学提供的ARIMA模型和Holt-Winters 模型理论借助于SPSS 软件计算出来。但该软件提供的自动建模功能较少。而R 语言则能提供多种强大的函数来实现SPSS 软件实现不了的功能，但缺点在于技术资料少，目前国内很少见到将R 语言应用到药品管理领域的文献。本次研究尝试使用R 语言编程进行历史数据分析并建模和预测，从而摸索出一套数据分析模式，再将这种方法推广到本院其他制剂生产预测中，改进药品管理决策。

1 研究工具

本次研究使用R 语言软件（版本3.6.0）提供的auto.arima、naive、snaive、ets、hw 这5 种自动建模函数。其中，auto.arima 函数用于自动寻找最佳ARIMA 模型，naive 函数用于建立不带漂移项的随机游走模型并返回预测数据，snaive 函数用于建立季节性随机游走模型并返回预测数据。此外本次研究还将使用2 种Holt-Winters 模型的建模函数，一个是ets 函数，另一个是hw函数。hw 函数是ets 函数的便捷包装，函数中有事先默认设定的参数值［1］。

2 研究方法

2.1 研究模型的建立 本次研究选取本院制剂室生产的小儿盐酸麻黄碱滴鼻液作为研究儿童用药销售规律的切入点，采集在2012 年1 月—2019 年12 月每月出库数量作为时间序列的数据，以2012 年1 月—2019 年6 月数据作为历史数据建模并预测未来6 个月的需求量，以2019 年7—12 月数据用于检验预测结果的对照。本次研究将使用上述5 种函数分别对历史数据自动建立ARIMA 模型和Holt-Winters 模型来预测6 个月的市场趋势，用W检验对这些模型的平稳性进行检查，使用MAPE 函数比较预测结果与对照数据的误差，选取误差最小的模型为最佳模型，从而建立起时间序列预测的方法学。

2.2 数据来源和预处理 本次研究将小儿盐酸麻黄碱滴鼻液在2012 年1 月—2019 年12 月期间每月从制剂室出库到药房的销量折算成每月出库的生产批次数量，见表1。将这些出库批数部分保存在y.csv 文件中，示意图见图1（限于篇幅，图1 仅列举前6 个月的数据）。

表1 源数据

代码和解释如下：

install.packages（"Metrics"）#下载并安装Metrics软件包；

install.packages（"forecast"） #下载并安装forecast软件包；

library（Metrics）#加载Metrics 软件包；

library（forecast）#加载forecast 软件包；

yaopin = read.csv ('s：\y.csv',header=T) #读取S 盘的y.csv 文件并赋值给“yaopin”的数据框；

shixubiao ＜-ts（yaopin，frequency=12，start=2012）#将yaopin 数据框的数据建立时间序列并将结果赋值给“shixubiao”的向量；

shuju＜-window（shixubiao，start=2012，end=2019+5/12）#将2012 年1 月—2019 年6 月数据用于建模，并用window 函数将数据赋值给“shuju”的向量；

shijizhi＜-window (shixubiao,start=2019+6/12) # 将2019 年7—12 月数据赋予“shijizhi”的向量，用于与预测值的比对。

图1 y.csv 文件的内容

3 研究步骤

3.1 数据初步考察

3.1.1 绘制时序图 求得数据框yaopin 的8 年所有数据平均值，绘制向量shixubiao 的时序图，从而获得对整个数据的初步直观印象。即：每月该药品的出库批数起伏很大，但在2012—2017 年基本保持在一个范围之中。从2018 年下半年开始到2019 年底，出库批次有了明显的增加。具体见图2。

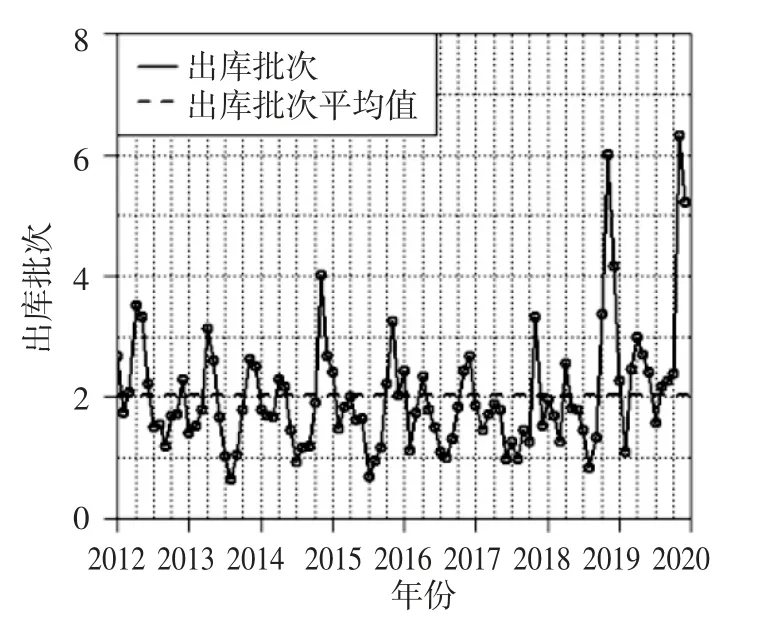
图2 每月出库批数时序图

代码如下：

y1＜- as.numeric（unlist（yaopin））#转换为数值型向量并赋值给y1；

plot（shixubiao，xaxs="i",yaxs="i",xlab="年份",lty=1,lwd=2,type="o", ylab="出库批次", xlim=c(2012,2020),ylim=c(0,8)) # 对8 年的时间序列数据作图，见图2；axis(1,c(2012,2013,2014,2015,2016,2017,2018,2019),labels=c("2012","2013","2014","2015","2016","2017","2018", "2019")) # 图2 横坐标分设别为2012—2019 年；abline(h=mean(y1),lty=2,lwd=2) #求所有出库批次平均值并将数值加载图上，见图2；grid（32,8,lty=3,col="black"）#添加网格线；legend（2012,8,c（"出库批次","出库批次平均值"），lwd=2，lty=c（1，2））#添加图例。

3.1.2 绘制历年相同月份数据对比图 以12 个月份为横坐标，以出库批次为纵坐标，将2012—2019 年的数据绘制于图3，每条线代表某一年的出库批次变化。该药品呈现明显的季节性变化，每年药品出库几乎都有两个高峰，说明该药品需求受到季节的影响。可以对该时间序列进行进一步的季节分解。具体见图3。

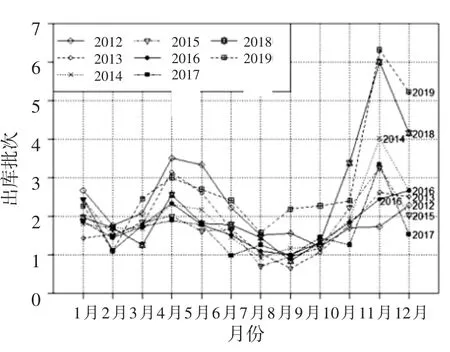
图3 历年相同月份数据对比图

代码如下：

year2012=yaopin[1：12,] #将数据框yaopin 的前12个数据作为2012 年的出库批次数据赋值给year2012；

year2013 = yaopin [13：24,]；year2014 = yaopin[25：36,];year2015=yaopin[37：48,];year2016=yaopin[49：60,];year2017 = yaopin [61：72,]; year2018 = yaopin[73：84,];year2019=yaopin [85：96,]#分别将yaopin 其余数据作为2013—2019 年数据赋值给向量year2013-year2019

plot(year2012,pch=5,ylim=c(0,7),xlim=c(0,13),xaxs="i",yaxs="i",xaxt="n", xlab="月份", ylab="出库批次") #将2012 年的12 个月数据描点绘图；

points (year2013,pch=1);points (year2014,pch=4);points(year2015,pch=25);points(year2016,pch=16);points(year2017,pch =15);points (year2018,pch =11);points(year2019,pch=12) #分别将2013—2019 年的数据用不同点绘图；

lines(year2012,lty=1); lines(year2013,lty=2); lines(year2014,lty=3);lines(year2015,lty=4);lines(year2016,lty=1);lines(year2017,lty=6);lines(year2018,lty=7);lines(year2019,lty=8)#分别将2012—2019 年的数据用线段绘图

axis(1, c(1：12), labels=c("1 月","2 月","3 月","4 月","5 月","6 月","7 月","8 月","9 月","10 月","11 月","12月")) #分别用1—12 月标记X轴刻度

grid(13,7,col="black",lty=3)#添加网格线

legend(0,7,c("2012","2013","2014","2015","2016","2017","2018","2019"),ncol=3,pch=c(5,1,4,25,16,15,11,12),lty=c(1,2,3,4,1,6,7,8)) #添加图例。

3.2 检查白噪声 在进行时间序列分析之前，必须先计算相关Ljung-Box 统计量的P值来证明该序列不是白噪声。如果P值显著大于显著性水平，那么就说明该序列没有任何统计规律可循，就得停止对该序列进行统计分析［2］。检查结果见表2。使用Box.test 函数对shixubiao 数据进行上述检查，发现该序列不是白噪声，可被预测和建模。

代码如下：

表2 时间序列的白噪声检验

Box.test (shixubiao, type="Ljung-Box",lag=6) # 检查Ljung-Box 统计量，拖尾因子为6;

Box.test(shixubiao, type="Ljung-Box",lag=12) # 检查Ljung-Box 统计量，拖尾因子为12。

3.3 季节性周期考查

3.3.1 季节性周期分解与绘图 使用decompose 函数对该时间序列的季节性周期进行分解，可以得到季节因子、趋势因子和随机因子，对这些因子数据进行作图，见图4。汇总季节因子数据见表3。

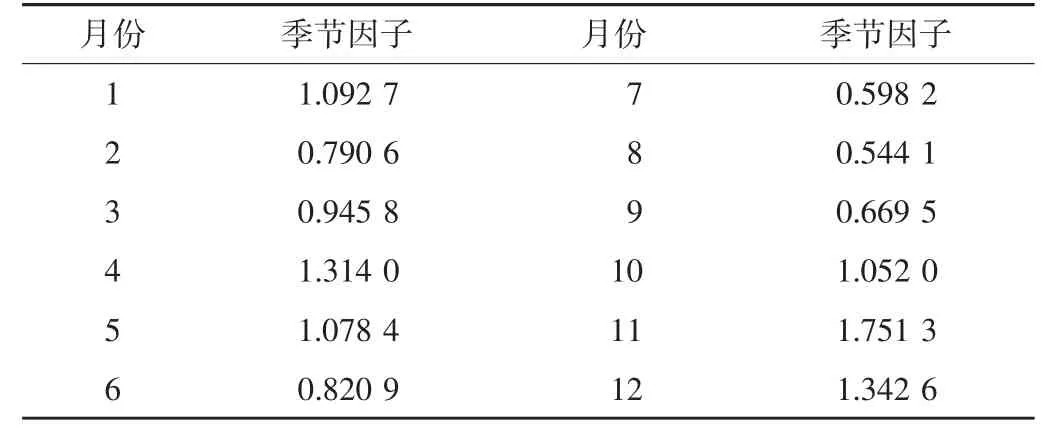
表3 季节因子数据表

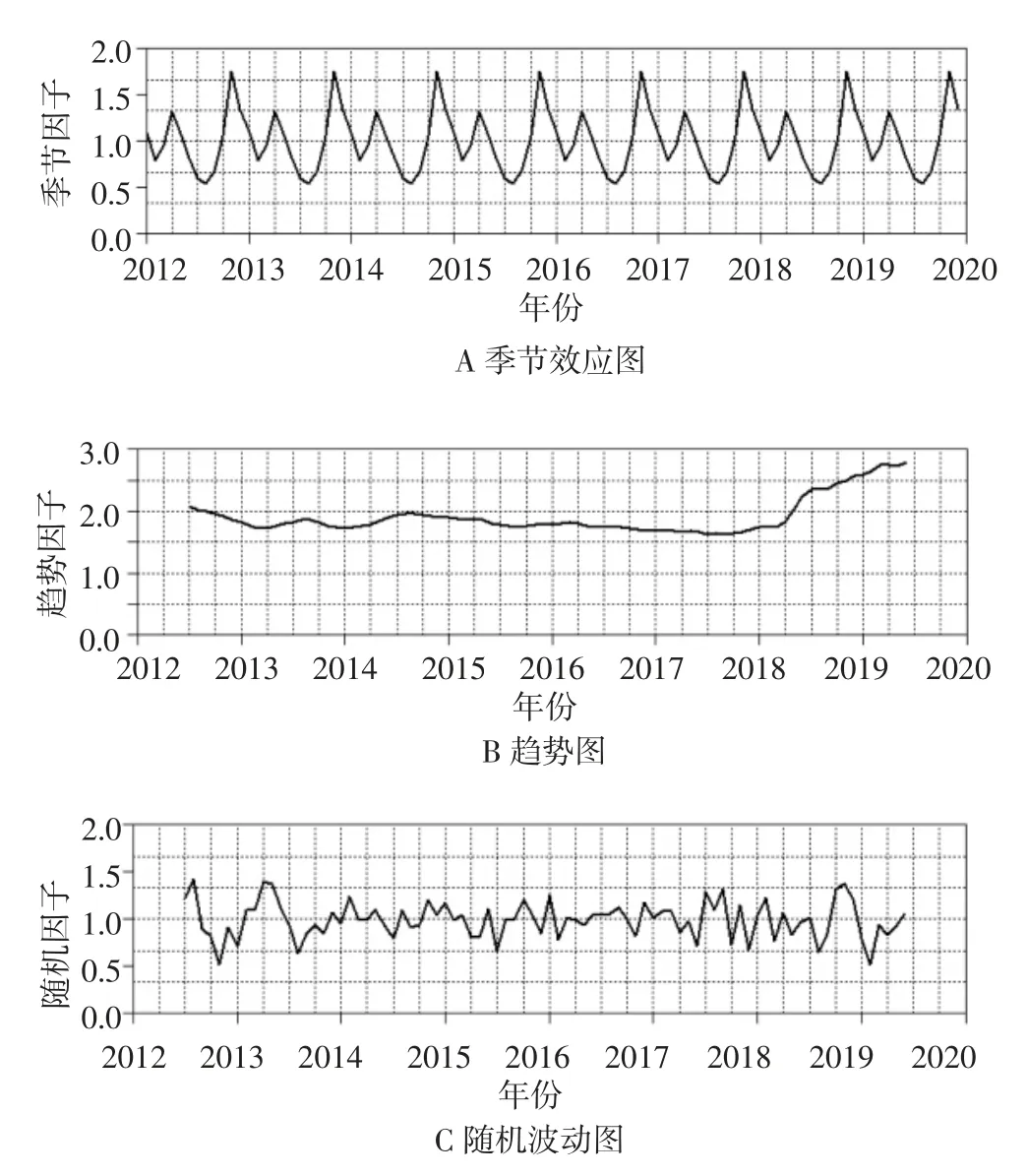
图4 季节分解图

代码如下：

jijie＜-decompose(shixubiao, type="multiplicative")# 将向量shixubiao 进行季节性分解并将结果赋值给jijie 的列表；

plot(jijie＄seasonal,xaxs="i",yaxs="i",xlab="年份",lwd=2,ylab=" 季节因子",xaxt="n",main="A 季节效应图",xlim=c(2012,2020),ylim=c(0,2)) # 将向量jijie 的季节因子数据绘图，见图4-A；

axis(1,c(2012,2013,2014,2015,2016,2017,2018,2019,2020),labels=c("2012","2013","2014","2015","2016","2017","2018","2019","2020")) #将横坐标刻度分别用2012—2019 表示，见图4-A；

grid(32,6,lty=3,col="black")#添加网格线。见图4-A。

plot(jijie＄trend,xaxs="i", yaxs="i",xlab="年份",lwd=2,ylab="趋势因子", xaxt="n", main="B 趋势图",xlim=c(2012,2020),ylim=c(0,3)) #将向量jijie 的趋势因子数据绘图，见图4-B

axis(1,c(2012,2013,2014,2015,2016,2017,2018,2019,2020),labels=c("2012","2013","2014","2015","2016","2017","2018","2019","2020")) # 将横坐标刻度分别用2012—2019 表示，见图4-B；

grid(32,6,lty=3,col="black")#添加网格线，见图4-B。

plot(jijie ＄random,xaxs="i",yaxs="i",xlab="年份",lwd=2,ylab=" 随机因子",xaxt="n", main="C 随机波动图",xlim=c(2012,2020),ylim=c(0,2)) # 将列表jijie 的随机因子数据绘图，见图4-C；

axis(1,c(2012,2013,2014,2015,2016,2017,2018,2019,2020),labels =c ("2012","2013","2014","2015","2016","2017","2018","2019","2020")) # 将横坐标刻度分别用2012—2019 表示，见图4-C；

grid(32,6,lty=3,col="black")#添加网格线，见图4-C。

jijie＄figure #提取列表jijie 的季节因子数据

3.3.2 季节性考查结果 图4-A 可以看出，该时间序列呈现每年两次的季节性波动。图4-B 图可以看出，出库批次的发展趋势是2012—2018 年上半年相对稳定，从2018 年下半年开始有明显的升高。图4-C 图可以看出，该药品随机因子基本上保持在0.5～1.5 之内。表3 可以看出，11 月的数值最高，其次是12 月和4 月，而8 月是全年最低值，这提示该药品在每年的用药高峰出现在11—12 月，其次是4 月。8 月份为全年用药低谷。

3.4 自动预测 对上述数据进行5 种模型预测，预测时间为6 个月，置信区间为95%。方法：使用forecast 软件包里的naive、snaive、hw 函数分别对向量shuju 进行自动建模同时并预测，预测后的数据分别赋值给yuce_naive、yuce_snaive、yuce_hw 的列表中。使用ets 和auto.arima 函数分别对向量shuju 进行自动建模，再用forecast 函数对建模后的数据进行预测，预测后的数据分别赋值给列表yuce_ets 和yuce_arima。

代码如下：

yuce_naive＜-naive(shuju,h=6 ,level = c(95))

yuce_snaive＜-snaive(shuju,h=6,level = c(95))

yuce_hw＜-hw(shuju,h=6,seasonal= "multiplicative",level = c(95))

yuce_ets＜- forecast(ets(shuju),h=6,level = c(95))

yuce_arima＜- forecast(auto.arima(shuju),h=6,level =c(95))

3.5 模型检查 时序拟合某一模型之后，需要检查平稳性，不平稳的模型是不能用来预测的。如果该模型是适用的，那么拟合残差应该是一白噪声序列［3］。为此，可以使用shapiro.test 函数分别对上述5 种函数建模结果的残差值＄residuals 列元素进行W检验，从而判断是否为白噪声序列。通过W检验发现，snaive、auto.arima 这2 个函数建立的模型残差P＜0.05，说明模型中有用的信息没有被充分提取，予以舍弃。W检验结果见表4。

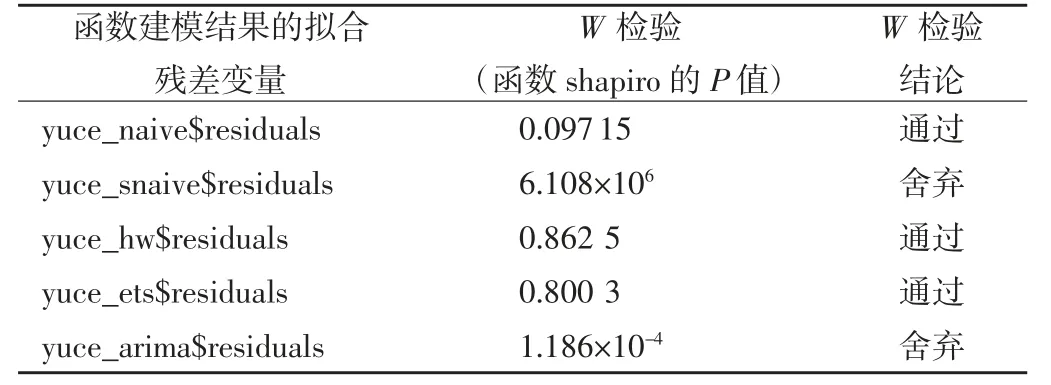
表4 五种函数建模结果的白噪声检查对照表

代码如下：

shapiro.test (yuce_naive ＄residuals)

shapiro.test (yuce_snaive ＄residuals)

shapiro.test (yuce_hw ＄residuals)

shapiro.test (yuce_ets ＄residuals)

shapiro.test (yuce_arima ＄residuals)

3.6 模型筛选

3.6.1 拟合优度对比 使用MAPE 函数对剩余3 个函数的预测平均值＄mean 列元素分别与向量shijizhi 里的实际值进行拟合优度对比（MAPE 值越小，说明建模的误差越小）。返回的yuce_naive、yuce_hw、yuce_ets 的MAPE 值分别为0.549 6、0.256 5、0.376 8。

代码如下：

mape(yuce_naive ＄mean,shijizhi)

mape(yuce_hw ＄mean,shijizhi)

mape(yuce_ets ＄mean,shijizhi)

3.6.2 三种函数预测误差的考查 分别提取上述剩余3 个函数预测结果的＄mean 列元素，返回各个函数预测的6个月预测平均值。将该值与2019 年9—12 月实际数据值汇总并逐个进行比对。见表5。

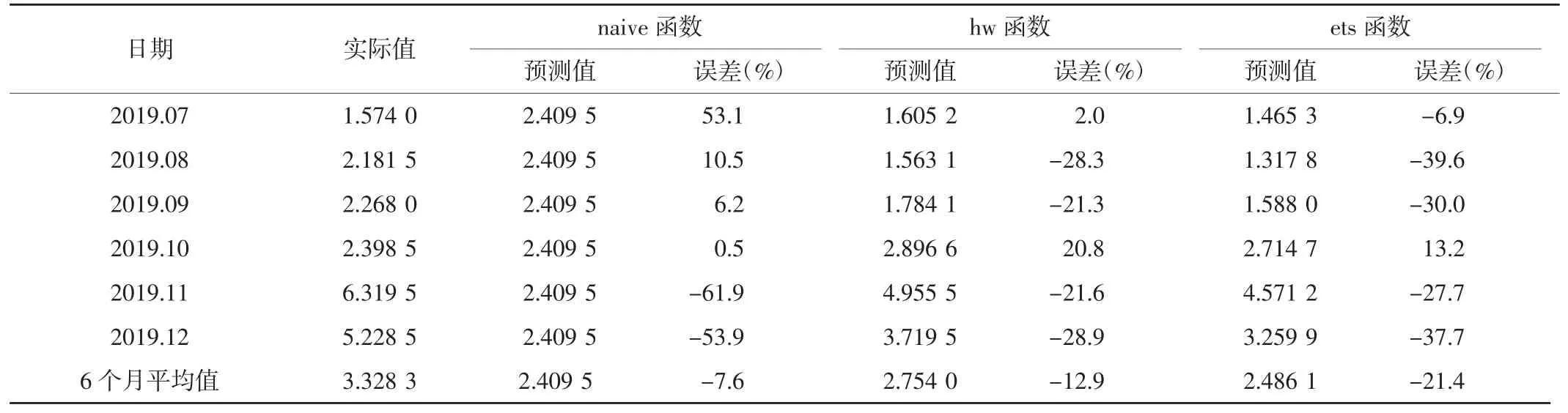
表5 三种函数建模所得到的近6 个月预测平均值和实际值与误差对照表

代码如下：

yuce_naive＄mean

yuce_hw＄mean

yuce_ets＄mean

3.6.3 建模函数筛选结果 根据“3.6.1”项下结果，hw函数的预测平均值与实际值误差的MAPE 值最小。而表5 中的3 种函数预测平均值与实际值的详细对比也证实了hw 函数建模的误差最小。2019 年7—12 月hw函数预测平均值为2.4 个批次，实际平均值3.2 个批次，两者平均误差-12.9%。因此，本次研究选择hw 函数模型作为拟合模型。

提取列表yuce_hw 里的＄model 列元素，得到hw函数自动拟合模型的相关参数。

代码如下：

yuce_hw＄model#提取列表yuce_hw 里的＄model 列元素；

该平滑参数为：α= 0.584 8，β=3×10-4，γ=1×10-4。

3.7 对筛选后的模型数据与实际数据进行绘图 使用plot 函数对该hw 函数建拟合与预测结果绘图，观察建模拟合值、预测平均值与实际值的直观效果。结果显示模型的拟合值、预测平均值图形与实际值图形比较接近。模型预测平均值与实际值虽然有一定误差，但也在预测区间的上限和下限之内。见图5。

代码如下：

plot(shixubiao,lwd=2,pch=19,type="b",lty=1，xaxs="i",yaxs="i",ylab="出库批次",xlab="年份",main="",xlim=c(2012,2020),ylim = c(0,9)) #将8 年历史实际值用实线和实心圆点表示

lines(yuce_hw ＄fitted,lwd=2,lty=2,pch=1,type="b") #将hw 函数拟合的7 年半模型数据用虚线和空心圆圈绘图

lines (yuce_hw ＄mean,lwd=2,lty=2,pch=6,type="b")#将hw 函数预测的6 个月平均值用虚线和空心倒三角形点绘图

U = yuce_hw＄upper ; L = yuce_hw ＄lower # 将hw 函数中的预测区间上限和下限数据分别赋值给U和L

points(U,pch=0); points(L,pch=0) #将hw 函数预测区间的上限和下限用空心方形点绘图，见图5；

lines(U, lwd=2,lty=4); lines(L, lwd=2,lty=4) # 将预测区间的上限和下限的数据用点划线绘图；axis(1,c(2013,2014,2015,2016,2017,2018,2019),labels=c("2013","2014","2015","2016","2017","2018","2019")) # 将横坐标中间的刻度分别用2013-2019 表示

grid(32,9,col="black",lty=3) #添加网格线

legend(2012,8.5,c("实际值","模型拟合值","模型预测平均值"," 预测区间的上限和下限"),pch=c(19,1,6,0),lty=c(1,2,2,4)) #添加图例。

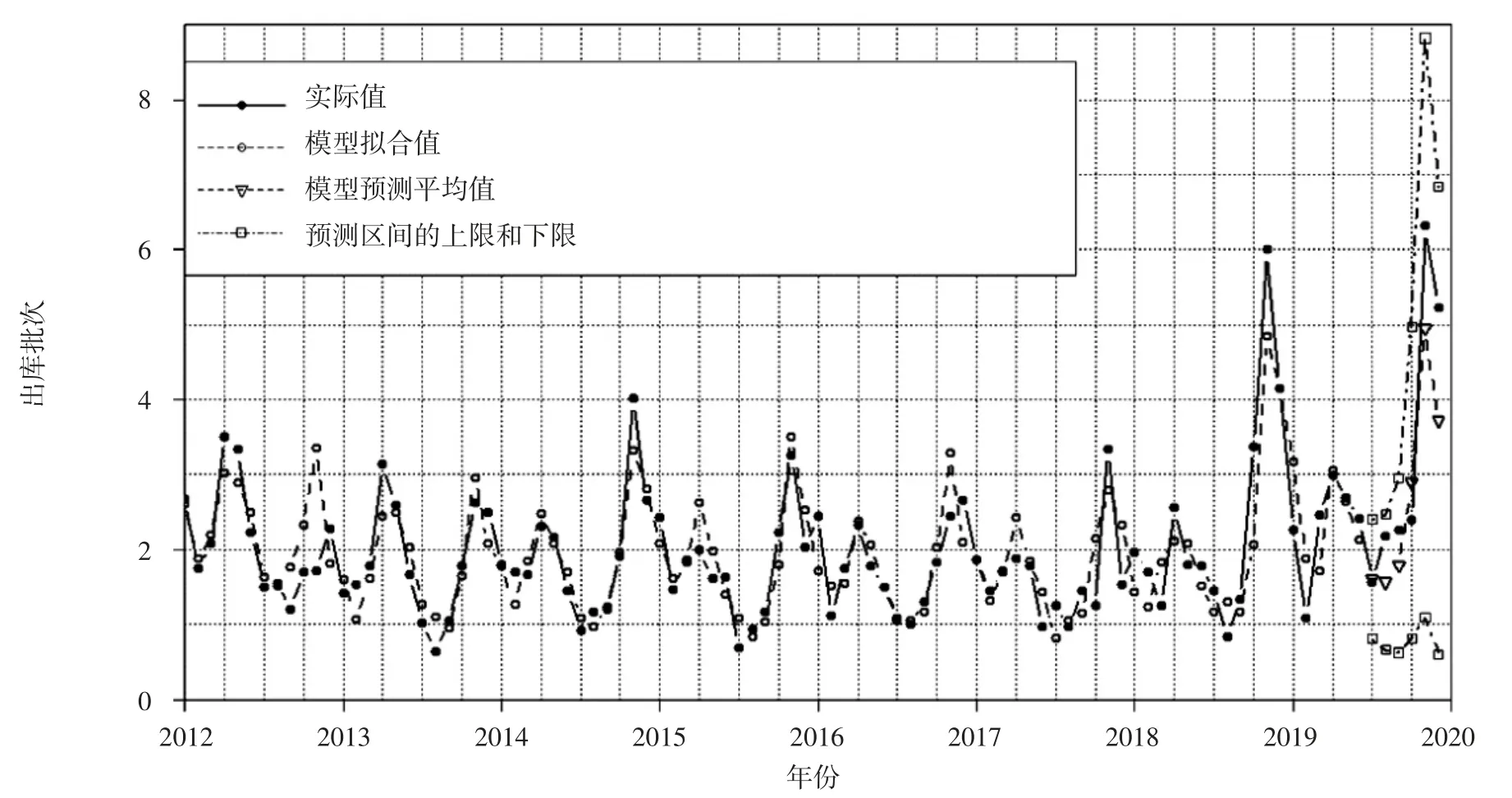
图5 hw 函数拟合预测结果与实际结果对照图

4 讨论

4.1 数据预处理 由于药品生产总是以批次为单位的，生产管理者更关注未来应当生产多少个批次的药品而不是多少支药，因此本次研究在对药品出库数据建模时使用了出库量与每批药品理论产量之比。例如，假设每批滴鼻液生产的理论数量是2 000 支，而当月制剂室出库了400 支给药房，那么当月的出库批次就是400/2 000=0.25 个批次。

4.2 建模函数的选择 虽然auto.arima 函数和ets 函数分别包含了naive、snaive、hw 函数自动建模的功能，但是其自动筛选的模型都有局限性。自动建模得到的结果并不一定是“最优”，理想的模型仍需研究者自行比较和判断［4］。

4.3 建模函数的预测误差 本次研究结果表明药品出库批次的实际值与预测平均值存在一定的误差，这些误差从-28.9%到20.8%之间。虽然这个误差范围较大，但是对于生产管理和决策者来说，已经足可以避免断药或药品生产过剩。

4.4 本药品的销售特征 小儿盐酸麻黄碱滴鼻液主要用于过敏性鼻炎和上呼吸道感染引起的鼻塞。在冬季的11 ～12 月，上呼吸道感染患者大量增加。而在每年春季的4 月，过敏性鼻炎患者增多，因而该药品销量也相应增多，在季节效应图上反映出了每年的这两个季节性波动。这提示管理者可以根据研究结果在高峰或低谷到来之前提前做好药品生产计划。

4.5 局限性 本次研究所采集的数据存在一定的局限性。首先，时间序列分析的研究前提是事件的发展通常具有一定的惯性［5］。但是就药品销售而言，这种需求惯性受到某种不确定性因素的限制，即一旦某种高致病性传染病突然在社会上大面积流行传播并且难以控制，就会影响相关药品销售数据预测的准确性。所以，虽然本次研究选择了hw 函数用于建模，但是一旦将来出库数据发生了变化，那么建模结果未必还是hw 函数。其次，本次研究受采集条件所限，将院内药房从制剂室领取的药品出库数据作为分析基础，但这只能间接反映药品销售，只有药房销售给患者的数据才是最直接的反映。因为药房领取的院内制剂总要积压一部分以备不时之需，这种人为占压库存的因素可能导致采集到的数据未必反映市场实时需求。下一步的研究是要采集药房的每月销售数据进行预测，探索更佳的拟合度。

综上所述，本次研究的重点不在于能否摸索到某个具体的建模函数，而是在于试图建立起预测药品市场需求量的方法学，从而为科学管理提供依据。虽然R语言初学较难，但是一旦建立起这种方法学就可以快速自动预测，便于日常工作。因此，本次研究的模式可以推广到本院制剂室的其他药品预测中去，也可为药厂等领域提供参考。