两种建筑围护结构动态热湿耦合传递模型对比与验证

陈友明，董文强，鲍洋，房爱民

（湖南大学 土木工程学院，湖南 长沙 410082）

多孔介质建筑围护结构中的热湿耦合传递对于围护结构的热湿性能、室内空气品质和结构耐久性具有显著影响.因此研究热湿耦合传递对预测和评估建筑围护结构内部的温度场和湿度场的分布、提高围护结构的热湿性能、抑止霉菌生长和提高结构耐久性具有重要的意义[1].

热湿耦合传递的研究已逾70 年，很多理论模型已被前人提出.然而，由于湿驱动势和假设条件的不同，各模型分别适用于不同的情况，而未有一广泛适用的模型来描述热湿耦合传递过程.Künzel[2]提出以相对湿度为湿驱动势建立热湿耦合模型，该模型把湿传递（蒸气传递、液态水传递）视为纯粹的扩散过程，均使用Fick 定律来描述，并使用3 个实验案例验证了该模型.该模型在WUFI 软件中得到进一步应用[3]。Liu&Chen[4]同样以相对湿度为湿驱动势建立热湿耦合模型，但该模型把液态水传递过程视为毛细压力驱动的一种“流”，使用Darcy 定律来描述，并使用EN 15026 案例[5]和HAMSTAD 基准案例[6-7]验证了该模型.两模型均未经过充分的全面验证——未进行实验验证或只进行了简单的实验验证。

Künzel 和Karagiozis[8]把热湿模拟模型的严格验证分为三步：1）模拟结果与解析解对比；2）模拟结果与具有明确的材料物性参数和边界条件的实验室测试数据对比；3）模拟结果与暴露于真实外部边界条件下的实测数据对比.而本文将对上述两模型进行全面验证，包括理论验证（与解析解对比）、模型间验证（与其他模型模拟解对比）和单/双侧受控条件下的实验验证.之所以选择这两个模型是因为：1）两模型的湿驱动势都是相对湿度，易于测量；2）在多层墙体交界面处的湿驱动势是连续的，这使得模拟计算易于实现.通过本文对这两种模型的对比和全面验证，以期发现两模型的优势与不足，为多孔建筑围护结构热湿耦合传递模型的研究提供参考.

1 两种模型

为了给研究者提供可靠的热湿耦合传递模型，以便准确地预测和评估多孔建筑围护结构的热湿分布和热湿性能，本文将对Künzel 模型和Liu&Chen模型进行全面验证.

全面验证包括理论验证、模型间验证和实验验证.在下文中所有的验证案例，两模型都使用Fortran程序和COMSOL 软件进行数值模拟.两模型的详细描述如下.

1.1 物理模型及假设条件

多层多孔墙体的热湿耦合传递过程如图1 所示.两模型的假设条件如下：不考虑空气传递；忽略重力效应；温度保持在0 ℃以上（忽略结冰和冻融影响）；孔隙内仅存在气液两相；湿空气被视为理想气体；仅考虑一维热湿传递.

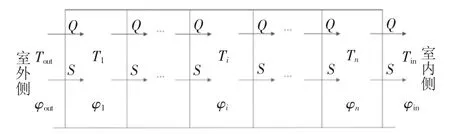
图1 多孔介质围护结构热湿耦合传递示意图Fig.1 Schematic diagram of coupled heat and moisture transfer of porous building envelopes

1.2 Künzel 模型

Künzel 模型[2]的湿、热控制方程分别为：

式中：δa=2×10-7× （T+273.15）0.81/Pambient，δa为静止空气的水蒸气渗透率，kg（/m·s·Pa）；μ 为水蒸气扩散阻力因子；Dw为湿扩散率，m2/s；Pambient为周围环境空气压力，Pa；φ 为相对湿度，%；T 为温度，K；t 为时间，s；Psat为饱和水蒸气分压力，Pa；w 为材料体积含湿量，kg/m3；ρm为干材料的密度，kg/m3；cp，m为干材料的比热容，J（/kg·K）；h1v为汽化潜热，J/kg；λ 为导热系数，W（/m·K）；cp，1为液态水的比热容，J（/kg·K）.

1.3 Liu&Chen 模型

Liu&Chen 模型[4]的湿、热控制方程分别为：

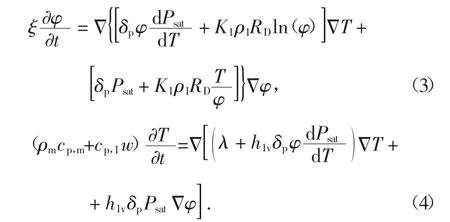
式中：δp为水蒸气渗透率，kg（/m·s·Pa）；K1为液态水渗透率，s；ρ1为液态水密度，kg/m3；RD为水蒸气气体常数，J（/kg·K）；ξ=∂w/∂φ 为等温吸放湿曲线的斜率，kg/m3.

1.4 边界条件

两模型使用相同的边界条件，太阳辐射被计入外部热边界条件.外/内部湿、热边界条件分别由下式给出：

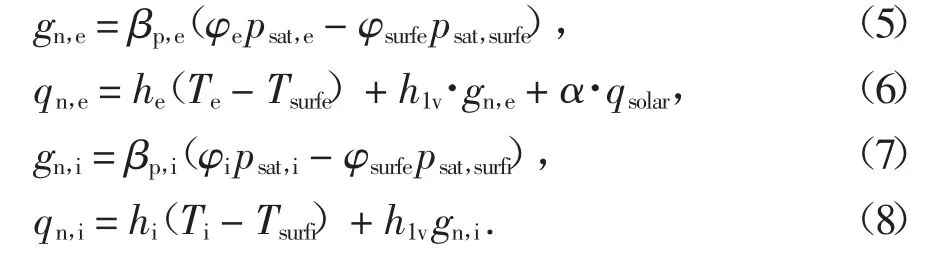
式中：gn为通过墙体表面的湿流，kg（/m2·s）；qn为通过墙体表面的热流，W/m2；βp为墙体表面的传质系数，kg（/m2·s·Pa）；φ 为空气相对湿度；φsurf为墙体表面相对湿度；psat为空气饱和水蒸气分压力，Pa；psat，surf为墙体表面饱和水蒸气分压力，Pa；h 为墙体表面的传热系数，W（/m·K）；T 为空气温度，K；Tsurf为墙体表面温度，K；α 为墙体外表面的太阳辐射吸收率；qsolar为太阳辐射强度，W/m2；下标e/i 分别表示墙体外/内表面.

1.5 两模型的区别

Künzel 模型统一采用Fick 扩散定律来描述水蒸气扩散量和液态水传递量[2，9].但实质上，液态水的毛细传递是一种“流”，而不是“扩散”.而且Künzel模型认为建筑材料内蒸气扩散、液态水传递这两种流动的方向相反，忽略了两种流动的相互作用，将二者看作两个相互独立的过程[10].

Liu&Chen 模型采用Fick 扩散定律来描述水蒸气扩散量；采用Darcy 定律来描述液态水传递量.且该模型中湿扩散系数Dw包含了液态水传递和水蒸气扩散两部分，也就是说Dw和K1、δp之间存在函数关系，关系式为K1=（Dwξ-δpP）sφ（/RDTρ1）[11].

1.6 模型求解方法

下文所有验证案例中，两模型都使用Fortran 程序和COMSOL 软件进行数值求解.在Fortran 程序中使用Crank-Nicholson 格式[12]离散热湿控制方程，使用牛顿迭代法把非线性方程组转化为线性方程组，使用高斯消元法求解线性方程组.使用Fortran 程序模拟时，时间步长范围为60～3 600 s，空间步长范围为2～10 mm，收敛标准为10-4，最大迭代次数为30.

2 模型验证

对Künzel 模型和Liu & Chen 模型的全面验证（理论验证、模型间验证和实验验证）在本节中实现.两模型都使用Fortran 程序和COMSOL 软件进行模拟.模拟结果和解析解、其他模型模拟解以及实验数据对比来验证两模型的准确性.同时也完成了两模型模拟结果之间的对比.用最大相对误差评估模拟结果与解析解、其他模型模拟解之间的一致性.用平均误差（ME）和均方根误差（RMSE）评估模拟结果与实验数据之间的一致性.

下文中，“Künzel+Fortran”、“Künzel+COMSOL”、“Liu&Chen+Fortran”和“Liu&Chen+COMSOL”分别是Künzel 模型和Liu&Chen 模型使用Fortran 程序和COMSOL 软件的模拟结果.

2.1 理论验证

采用HAMSTAD 基准案例2[6]作为理论验证的案例.该案例描述了等温条件下单层各向同性墙体的湿分布.由于不考虑室内外的温度差异，该案例可得到一解析解.外侧环境温度和相对湿度分别是20℃和45%，内侧环境温度和相对湿度分别是20 ℃和65%.墙体初始温度和相对湿度分别是20 ℃和95%.该墙体材料的热湿特性在文献[6]中给出.模拟持续1 000 h，100 h、300 h 和1 000 h 时墙体中含湿量分布结果如图2 所示.

图2 100 h、300 h、1 000 h 时墙体内的含湿量分布Fig.2 Moisture content profiles of the wall at 100/300/1 000 h

两模型使用Fortran 程序和COMSOL 软件的模拟结果与解析解的对比如图2 所示.Künzel+Fortran结果与解析解的最大相对误差在100 h、300 h、1 000 h 时分别为2.562%、1.06%、0.45%.相应地，Liu &Chen+Fortran 结果与解析解的最大相对误差在100 h、300 h、1 000 h 时分别为2.623%、1.072%、0.45%.可以看出，两模型的模拟结果与解析解之间吻合良好，且Fortran 程序与COMSOL 软件的模拟结果也是十分一致的.

2.2 模型间验证

采用HAMSTAD 基准案例5[6]作为模型间验证的案例.该案例分析了三层复合墙体的湿分布.三层墙体依次包含365 mm 的外部砖层、15 mm 的砂浆层和40 mm 的内部保温层.外侧环境温度和相对湿度分别为0 ℃和80%，内侧环境温度和相对湿度分别为20 ℃和60%.墙体初始温度和相对湿度分别为25℃和60%.每层材料的热湿特性在文献[6]中给出.模拟持续60 d.60 d 后墙体内的相对湿度和含湿量分布如图3 所示，其中，“TUD”是德累斯顿科技大学得到的模拟结果[6].

两模型使用Fortran 程序和COMSOL 软件的模拟结果与TUD 模拟结果的对比如图3 所示.Künzel+Fortran、Künzel+COMSOL 的相对湿度结果与TUD 模拟结果的最大相对误差分别为11.7%、10.1%.Liu&Chen+Fortran、Liu&Chen+COMSOL 的相对湿度结果与TUD 模拟结果的最大相对误差分别为1.58%、0.54%.可以看出，Fortran 程序与COMSOL 软件的模拟结果也是一致的.但在高含湿量段（相对湿度接近95%），Künzel 模型的模拟结果存在较大差别，而Liu&Chen 模型模拟结果与TUD 模拟结果非常一致.

2.3 单侧受控条件下的实验验证

采用一个处于单侧受控条件下的实验[13-15]来验证Künzel 模型和Liu&Chen 模型.实验材料选用苏格兰松，对测试样品在1 mm/4 mm/7 mm 厚度处的相对湿度和温度进行实验监测记录.苏格兰松的材料特性可在文献[15-18]中找到.边界条件如图4 中所示的“环境条件”.

两模型使用Fortran 程序和COMSOL 软件模拟计算得到4 mm 厚度处的相对湿度和温度值.模拟结果和试验数据的对比如图4 所示.

图3 60 d 后墙体内的相对湿度和含湿量分布Fig.3 Relative humidity and moisture content profiles at the end of 60 days

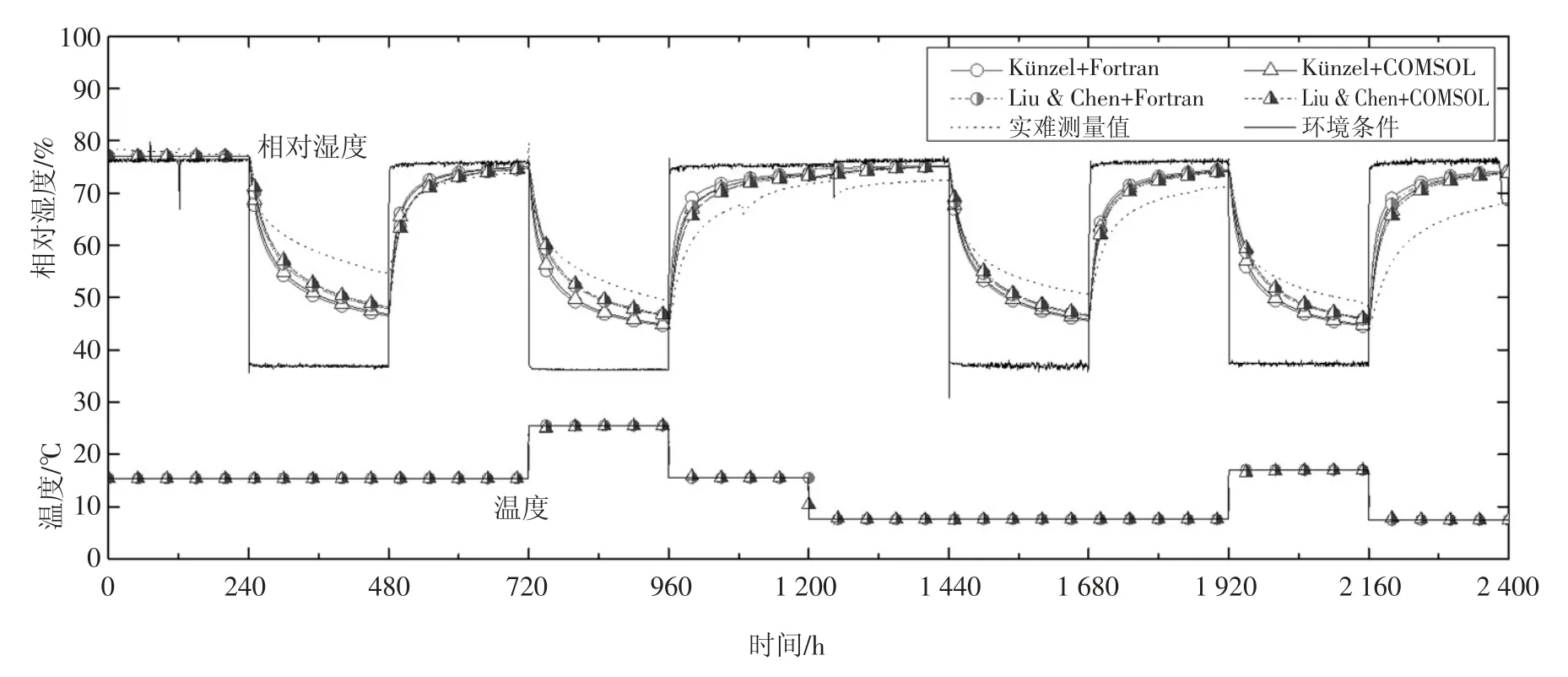
图4 在4 mm 厚度处模拟和实测结果的对比Fig.4 Comparison between the simulated and measured results at the depth of 4 mm

表1 在4 mm 厚度处模拟值与实测值之间的ME 和RMSETab.1 ME and RMSE between measured and simulated results at the depth of 4 mm

由图4 可看出，两模型模拟结果与实测值之间吻合良好.表1 给出了模拟值与实测值之间的ME和RMSE.相对湿度的ME 最大值为4.61%，温度的ME 最大值为0.11 ℃，相对湿度的RMSE 最大值为5.37%，温度的RMSE 最大值为0.44 ℃.两模型的模拟结果与实测值较吻合，且两模型模拟值非常一致.

2.4 双侧受控条件下的实验验证

采用一个处于双侧受控条件下的实验[19]来进一步验证两模型的准确性.该实验在双气候室中进行.对两侧的气候室和被试墙体内部的相对湿度和温度进行实验监测记录.测试墙体的构造和每个墙体中温湿度传感器的位置如图5 所示.关于气候室、边界条件、测量仪器和墙体材料特性的详细描述参见文献[19-22].将Künzel 模型和Liu&Chen 模型使用Fortran 程序和COMSOL 软件模拟得到的结果与实测值比较来验证两模型的准确性.实验测试了4 个墙体，本研究对这4 个墙体进行了模拟和比较.考虑到篇幅限制，这里仅给出误差较小的1#墙体和误差较大的4#墙体的部分结果.

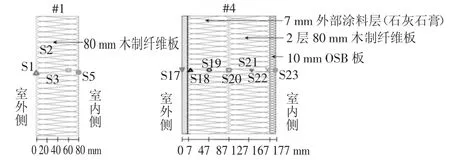
图5 测试墙体的构造和温湿度传感器的位置Fig.5 Schematic of the wall configurations and the sensor locations in the tested walls

2.4.1 1#墙体

1#墙体由80 mm 的木制纤维板组成.图6 给出了1#墙体中40 mm 厚度处的模拟结果与实验结果的对比.由图6 可知，相对湿度的模拟值几乎总是高于实测值，且两模型各模拟结果表现出相同的趋势，与实测结果之间存在一定差异.从表2 可看出，1#墙体中40 mm 厚度处相对湿度和温度的各模拟结果的ME 和RMSE 非常接近.相对湿度的ME 最大值为2.97%，RMSE 最大值为3.46%；温度的ME 最大值为0.24 ℃，RMSE 最大值为0.34 ℃.模拟计算方法（Fortran 程序和COMSOL）对模拟结果几乎没有影响.两模型模拟结果与实测结果之间吻合良好.

图6 1#墙体中40 mm 厚度处的相对湿度和温度的模拟值与实测值的对比Fig.6 Comparison of relative humidity and temperature at the depth of 40 mm in Wall#1

2.4.2 4#墙体

4#墙体由7 mm 的外部石灰石膏涂层、160 mm的木制纤维板和10 mm 的内部OSB 板组成.图7～图9 给出了4#墙体中不同厚度处的模拟结果与实验结果的对比.由图7～图9 可知，不同厚度处的两模型各模拟结果表现出相同的趋势，但和实测结果之间仍有差异，且在167 mm 厚度处的相对湿度模拟结果与实测结果偏差较大.

表2 1#墙体中40 mm 厚度处模拟值与实测值之间的ME 和RMSETab.2 ME and RMSE between measured and simulated results at the depth of 40 mm in Wall#1

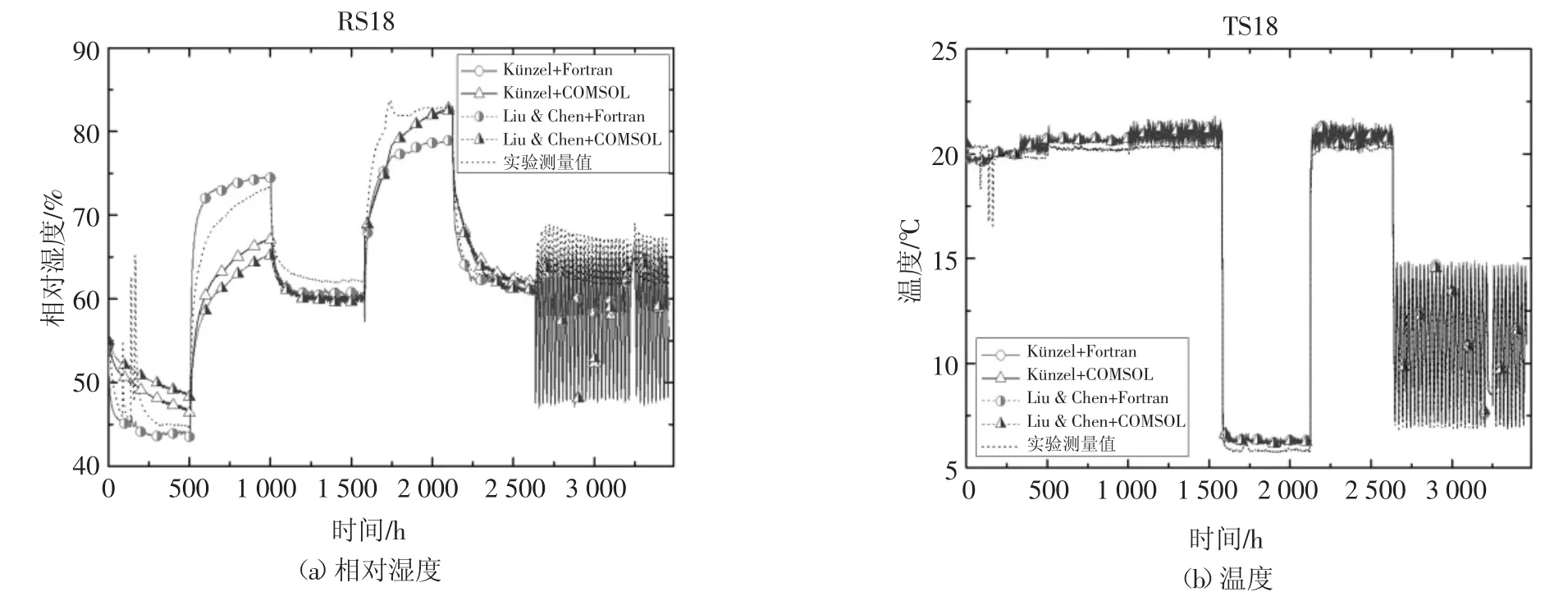
图7 4#墙体中7 mm 厚度处的相对湿度和温度的模拟值与实测值的对比Fig.7 Comparison of relative humidity and temperature at the depth of 7 mm in Wall#4

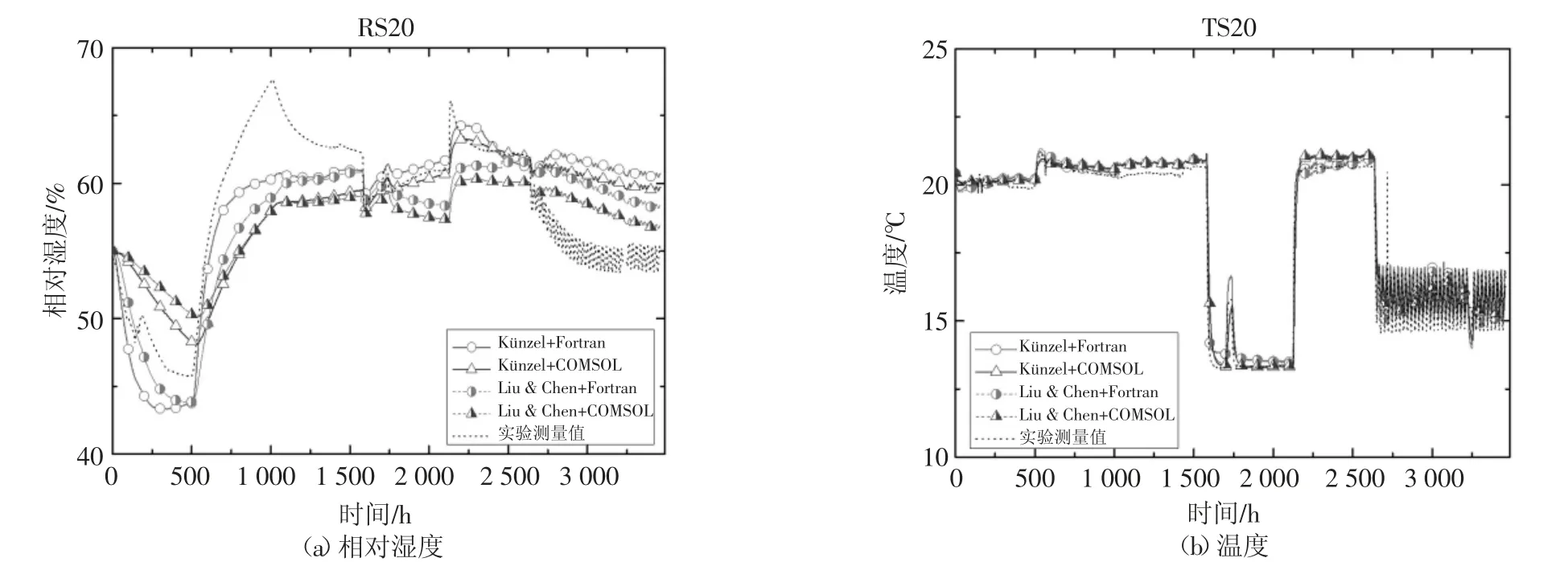
图8 4#墙体中87 mm 厚度处的相对湿度和温度的模拟值与实测值的对比Fig.8 Comparison of relative humidity and temperature at the depth of 87 mm in Wall#4

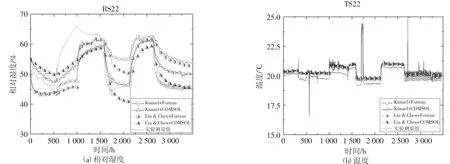
图9 4#墙体中167 mm 厚度处的相对湿度和温度的模拟值与实测值的对比Fig.9 Comparison of relative humidity and temperature at the depth of 167 mm in Wall#4

表3 给出了4#墙体不同厚度处的相对湿度和温度模拟值的ME 和RMSE.4#墙体中不同厚度（除了167 mm 厚度处外）的两模型各模拟结果的ME 和RMSE 很接近.不同厚度的相对湿度的ME 在2.81%～6.25%之间，RMSE 在2.04%～7.52%之间；温度的ME 在0.26～0.51 ℃之间，RMSE 在0.32～0.50 ℃之间.模拟计算方法（Fortran 程序和COMSOL）对模拟结果有一定的影响，在167 mm 厚度处的这一影响较大.两模型模拟结果与实测结果之间吻合，且相对湿度和温度的ME 和RMSE 都在数值模拟可接受的范围内.

表3 4#墙体中不同厚度处模拟值与实测值之间的ME 和RMSETab.3 ME and RMSE between measured and simulated results at different depths in Wall#4

上述两个实验验证案例通过两种模拟方法（Fortran 程序和COMSOL 软件）验证了Künzel 模型和Liu&Chen 模型的准确性.模拟值和实测值之间仍然存在一定的误差，且相对湿度比温度的误差更大.误差来源主要有三方面：1）测量方法和传感器的误差；2）材料特性及输入参数的差异；3）模型的差异.这其中，模型本身的不足体现在误差上更加明显——模型在高相对湿度段不能准确模拟.多孔介质建筑材料中的湿传递可分为两种流——蒸气扩散和液态水传递.两模型都使用相对湿度作为湿驱动势，在低相对湿度段（吸湿区），水分主要通过蒸气扩散传递，此时使用相对湿度作为湿驱动势是合理的.但随着相对湿度的增大，附着在孔隙中的液态水越来越多，毛细压力驱动下的液态水传递作用越来越强.当相对湿度达到或超过95%时（超吸湿区），水分主要通过液态水传递，此时的主要驱动势是毛细压力.在吸湿区与超吸湿区间某一范围内，蒸气扩散和液态水传递是共存的[23].因此，随着相对湿度的增加，以相对湿度作为驱动势的模型越来越不准确，模拟值与实测值间的误差增大.

上述4 个验证案例中，Künzel 模型和Liu &Chen 模型的模拟结果与解析解、其他模型模拟解和实验数据之间有良好的一致性.当相对湿度较低时，Künzel 模型和Liu&Chen 模型的模拟结果间的差异很小，且相对湿度模拟值的误差都比温度模拟值的误差大.当相对湿度逐渐增大直至超出吸湿区范围时，模拟值与现有对比值（其他模型模拟解或实验数据）的偏差逐渐变大.Liu&Chen 模型的模拟结果比Künzel 模型更接近现有对比值，这在图3 中尤为明显，当相对湿度逐渐接近95%时，Künzel 模型已经不再能够准确模拟湿分布.

3 结论

本文对两种以相对湿度为湿驱动势的热湿耦合传递模型（Künzel 模型和Liu&Chen 模型）进行了全面验证——理论验证、模型间验证和实验验证.用自编程的Fortran 程序和COMSOL 软件对两模型进行数值模拟.验证结果表明，两模型的模拟结果与解析解、其他模型模拟解和实验数据有良好的一致性.两模型的相对湿度模拟值的误差都比温度模拟值的误差大，这些误差来源于相对湿度传感器测量的不准确、模拟用的材料特性与实际值不同、计算输入参数与实际值的差异和模型本身的不足.

本文对Künzel 模型和Liu & Chen 模型进行了对比，结果表明：

1） 当相对湿度较低时，Künzel 模型和Liu &Chen 模型的模拟结果间的差异很小.

2）当相对湿度逐渐增大直至超出吸湿区范围时，模拟值与对比值的偏差逐渐变大，Künzel 模型不能准确模拟湿分布.

通过两模型的对比，模型模拟结果与解析解、其他模型模拟解、实验结果在吸湿范围内吻合良好，从而在吸湿范围内充分验证了两个模型.而在吸湿区末段（相对湿度小于但接近95%），Liu&Chen 模型比Künzel 模型更准确和可用.至于超出吸湿区范围时（相对湿度>95%），两模型的适用性有待下一步研究.

这项研究为多孔建筑围护结构热湿耦合传递领域的研究人员在预测建筑围护结构内的温度和水分含量分布、改善建筑物湿热性能、预测霉菌生长风险以及提高结构耐久性等方面的进一步分析和研究提供了依据。