粗粒土压实特性与高填体沉降规律研究

黄崇伟， 郭丹丹， 王德荣， 张道玲

（1. 上海理工大学 管理学院，上海 200093；2. 陆军工程大学 国防工程学院，南京 210007；3. 上海华东民航机场建设监理有限公司，上海 200335）

我国中西部地区大多为山地和丘陵，地形、地貌和地质条件复杂，高填体沉降控制困难[1]。影响高填体沉降变形的因素很多，其中最基本的是粗粒土种类及其力学参数。Bagherzadeh-Khalkhali等[2]通过不同粒径粗粒土试验和离散元数值模拟方法，研究了粒径、应力水平对于粗粒土抗剪强度的影响，以及直剪试验微观力学行为，研究结果表明级配改变对于粗粒土的力学性质有着重要的影响。Fu等[3]研制了一种改进型直剪试验仪器，给出了剪切箱间隙和试样尺寸对粗粒土抗剪性能的影响，试验结果表明，间隙大小和试件尺寸对粗粒土的抗剪性能均有显著影响。Liu等[4]采用大型三轴剪切仪对大坝粗集料抗剪性能进行了试验研究，结果表明抗剪强度参数随围压的增大而减小，其破坏包络线为凸曲线；在低围压下具有明显的曲率，在中等围压下膨胀被颗粒破碎所抵消，在高围压下膨胀消失等规律。凌华等[5]通过8组不同细粒含量粗粒土的大型三轴排水剪切试验，研究了级配对粗粒土强度、变形、剪胀特性和颗粒破碎的影响，结果表明细颗粒含量的大小、含泥是影响粗粒土力学特性的重要因素。国内外学者针对粗粒土本构模型也开展了较多的研究。Chen等[6]通过大型固结不排水和大型固结排水三轴试验、扫描电子显微镜、能量色散X射线和风化分解测试等方法，研究了粗粒土加筋力学特性及微观结构，并基于试验数据讨论了粗粒土加筋本构模型的参数。孔郁斐[7]通过各主要因素影响下的土石混合料压缩性质研究，提出了考虑填料剪切蠕变及压缩蠕变的流变本构模型，研究了高填方地基的长期变形特性。Kong等[8]讨论了粗粒土的主要特性，建立了粗粒土的弹粘塑性模型，模拟了粗粒土的剪切和压缩时变特性。Sancak等[9]提出了一种基于结构使用极限的应变结构设计摩擦角参数取值方法。Isik等[10]制备了200种土壤混合物，并以标准击实试验压实，采用考虑不同输入数据集的神经网络模型，对压实参数进行了预测，结果表明，子聚类数据分割技术可以进一步提高神经网络模型的泛化能力和预测精度。Lins等[11]利用非饱和干燥粗粒土，通过一系列模型基础和压缩试验确定并预测了粗粒土极限承载能力及弹性模量。陈生水等[12]针对高填粗颗粒土流变特性，以应力、应变及时间为基本变量，提出了统一模拟粗颗粒土变形、流变、应力松弛等性质的弹塑性本构模型，并以此模拟和计算了施工过程的沉降量。

在填筑体沉降计算方面，Lee等[13]研究了疏浚土中细粒土层在沉降和自重固结完成后的体积和密度比，并基于此计算出最终的沉降值。Yang[14]基于粗粒土非线性粘塑性变形特性及merchant模型，建立了粗粒土路基的流变计算公式，并根据公式计算了长期荷载作用下的路基沉降，计算结果表明该公式比标准方法更为保守。Fargnoli等[15]利用经典高斯公式预测了粗粒土双隧道开挖的沉降预测，研究了不同开挖参数对粗粒土沉降槽体积损失和形状的影响。Li等[16]通过3种不同填料路基模型，验证了粗粒土加筋和水泥处治对于路基沉降控制的有效性，并探讨了粗粒土加筋路基模型荷载–沉降特性的相互作用及影响。魏星等[17]、吴俊等[18]、宋晶等[19]采用有限元、数值分析等方式模拟了填筑体沉降变形。梅国雄等[20]、曹光栩等[21]基于土体参数和沉降机理提出了填筑体沉降变形计算的简易方法。邢逸航等[22]通过数值分析、循环荷载三轴试验研究了长期车辆荷载作用对粗粒土路基的影响。在试验研究方面，刘丽萍等[23]、王玉锁等[24]对不同级配、不同粗粒含量及破碎率的土石混合料进行了击实试验，分析了击实功、击实方法及等效处理法对土石混合料击实结果的影响。

但工程实践证明粗粒土压实特性复杂，粗粒土压实效果对沉降的影响方面研究成果较少，然而机场高填料多采用粗粒土填筑，与细粒土沉降计算方法有本质的差别。本文面向中西部地区机场高填方粗粒土填料，拟开展大量的室内重型击实试验和压缩模量试验，研究粗粒土压实度与压缩模量间的相互关系，建立压缩模量的预估模型。基于室内试验的压缩参数建立高填体的有限元模型，计算多种填筑高度、多种压实度下高填体的沉降量，分析高填体的沉降规律，研究压实效果–填筑高度–填筑体沉降的关系，建立高填体沉降的多元回归方程，为高填体的沉降预估提供简便的方法。

1 试验方案

1.1 试验材料

试验材料取自中西部某机场现场的高填方粗粒土填料，为灰色碎石土，含块石，土石工程分级属Ⅳ级。根据《公路土工试验规程》的筛分法对土样开展颗粒分析试验，各级筛孔的通过百分率如图1所示。从图1中6个土样（S1～S6）的筛分曲线可知，该填料粒径位于2～20 mm的部分占总质量的80%以上，最大粒径小于40 mm，属于粗粒土。

图 1 填料的筛分曲线Fig.1 Screening curve of fillings

1.2 试验内容

1.2.1 最大干密度

最大干密度是研究土体压实特性的必要参数之一。对机场工程的粗粒土，应采取重型击实试验测试其最大干密度。重型击实试验的试筒内径15.2 cm，高 17 cm，筒体体积 2177 cm3。为获得粗粒土的最大干密度，分别在5种含水率（2%，4%，6%，8%，10%）下进行击实试验。首先将由现场运回的土样用烘箱烘干，然后称取每个试样干土8 kg。根据设计含水率的要求称取相应的水质量，倒入土样后充分搅拌，用塑料膜包裹后静置12 h，使得土水充分混合。将制备好的土样分3次倒入桶内，分3层击实，每层击实98次。开展3组平行试验，取平均值为该粗粒土的最佳含水率和最大干密度。

1.2.2 压缩模量试验

获得土体的最大干密度和最佳含水率之后，即可开展不同压实度的粗粒土的压缩模量试验。压缩模量试件成型方法如下：依据重型击实试验结果以及环刀体积，确定不同压实度的试件所需粗粒土的质量；压缩模量试件如图2所示。以相同含水率、压实度下3个平行试件作为一组，对应的荷载按照试验设计表取值来模拟不同的初始状态，荷载等级包括100，200，300，400 kPa。对不同含水率下的土样进行分级加载，获得各级荷载作用下变形与持荷时间的关系，并绘制出对应的孔隙比–压力（e–p）曲线，从而计算土样的压缩模量。

图 2 压缩模量试件Fig.2 Specimens of compression modulus

1.3 有限元模型

为了分析高填体的沉降规律，在获得土体最大干密度、压缩模量等计算参数后，采用有限元软件分析不同压实度、不同填筑高度的回填体的沉降。高填方有限元模型如图3所示。其底部宽100 m，高度根据计算工况确定。回填土体压缩模量根据不同计算目的，或有现场实测压实度数据绘制或计算所得，或为了敏感性分析目的，按含水率及压实度假设取值，其表泊松比以0.35为输入参数。土体单元类型为CPS4R，回填土体的单元网格尺寸为0.25 m，边坡坡度为1∶2；地基土的单元网格尺寸为0.5 m，压缩深度均统一取20 m。有限元模型仅约束底部的水平和竖向位移。高填体仅受到重力荷载的作用，其重力加速度近似取为9.8 m/s2。在分析土体沉降之前，首先对原地基进行了地应力平衡分析。

图 3 有限元模型Fig.3 Finite element model

2 试验结果与讨论

2.1 最大干密度

表1为重型击实试验的结果。从表1可知，土样实测含水率与设计含水率非常接近，试验中含水率控制良好。含水率在2%左右时，土样干密度最低；该粗粒土的最佳含水率在4%～8%之间。绘制土样含水率和干密度的关系曲线，如图4所示。从图4可得，测试土样最佳含水率为6.2%，最大干密度为2.13 g/cm3。试验发现土样整体的吸水性较差，在10%含水率的状态下已经很难成型。

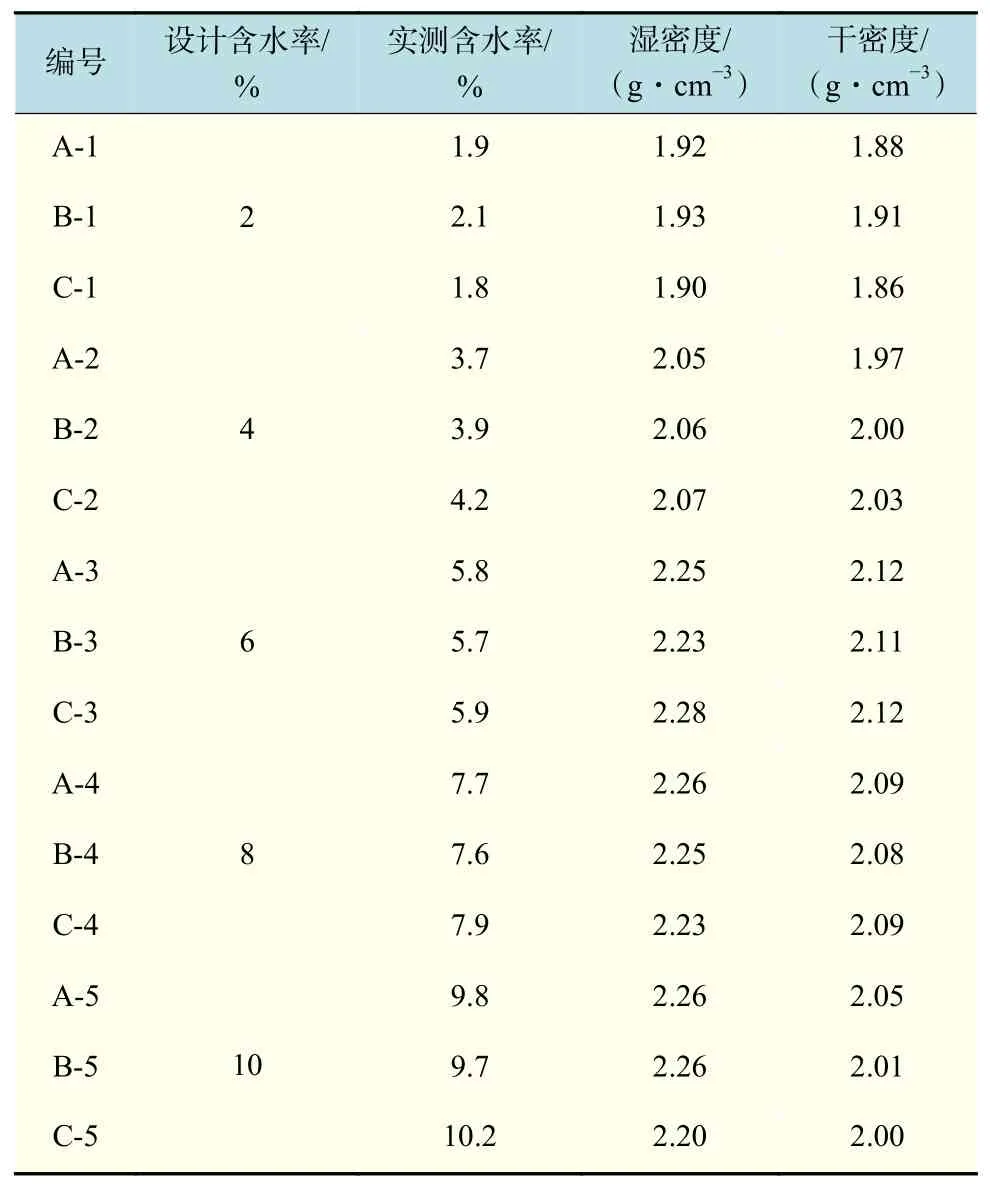
表 1 重型击实试验结果Tab.1 Test results of heavy compaction

2.2 粗粒土的压缩模量预估

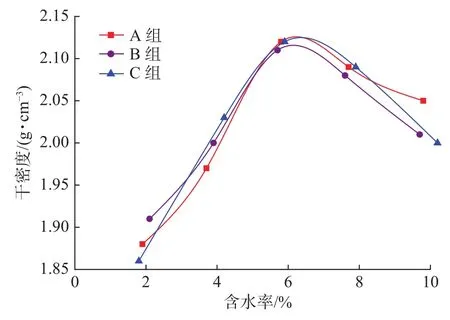
图 4 含水率与干密度关系曲线图Fig. 4 Curve of water content and dry density

如前文所述，采用压力机与环刀成型含水率分别为2%，4%，6%，8%和10%的试件，每个含水率3个平行试件。在成型过程中测定试件的成型质量，并与目标质量相比较，保证试件的成型精度。采用单轴固结仪法进行压缩模量试验，固结时间24 h。固结试验结束后，土样在不同荷载下的压缩变形如图5所示。随着含水率增加，土体的压缩变形量也逐渐增加，两者呈正相关关系。此关系随着荷载的增大而逐渐趋于线性关系，说明含水率对该土体压缩变形的影响随着荷载的增大而增大。在同一含水率下，土体的压缩变形随着荷载的增大而增大；在5种含水率下，试样在荷载为400 kPa时的压缩变形较100 kPa时的增幅依次为70.5%，41.9%，37.8%，33.1%和39.3%。可见，含水率较低时，荷载对压缩变形的影响增大。

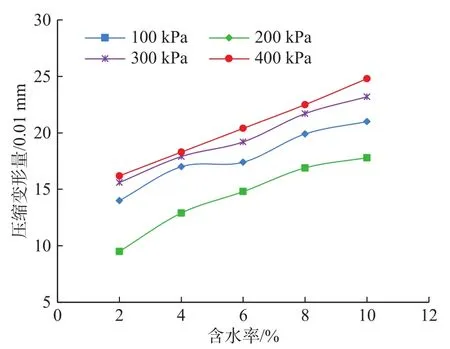
图 5 土体固结变形Fig.5 Consolidation deformation of soil

不同荷载下的孔隙比是计算土样压缩模量的必要参数。根据试验结果计算不同压力下的孔隙比，可以得到如图6所示的e-p曲线。同一含水率下，土样的孔隙比随着压力的增大而减小，两者有较好的相关性；孔隙比随着含水率的增大而减小，即含水率较低时，土样的孔隙比更大。基于图6的e-p曲线，可以计算不同压实度下土样的压缩模量。图7为所有的压实度与压缩模量的结果。

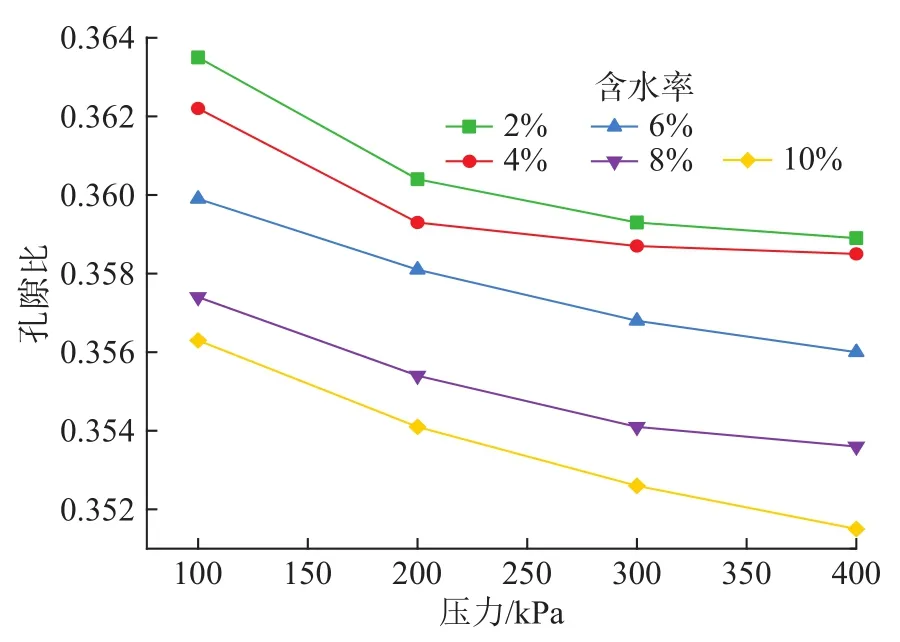
图 6 填料 e–p关系曲线Fig.6 e–p curve of fillings

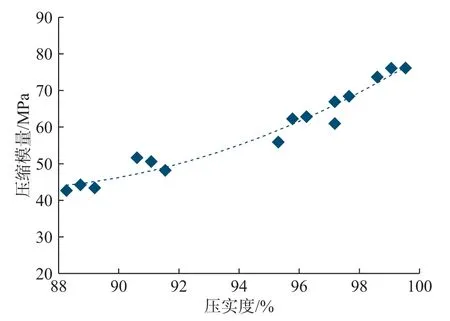
图 7 压实度与压缩模量的关系曲线Fig.7 Curve of the relationship between compaction and compression modulus

通过二次多项式拟合，可以得到压缩模量的预估方程

式中：x为压实度，85%≤x≤100%；Es为压缩模量。其相关系数R2=0.96，相关性良好。

2.3 填筑体沉降的多元回归分析

压缩模量是高填体沉降计算的重要参数，而粗粒土的压实度与其压缩模量具有良好的相关性。可以推测，压实度与高填体沉降也存在某种紧密的联系。为研究两者的相关性，采用有限元法计算不同压实度下的高填体的沉降量。

2.3.1 有限元模型验证

选取中西部某机场二标段高填方体实测沉降数据与有限元的结果对比，以验证模型的可靠性。该标段填筑体高度为25 m，沉降监测部位为原地基顶面与回填体顶面2个部位，分别用于检测原地基沉降及回填体本身沉降。沉降监测时间自2018年7月11日至2019年2月18日，历时222 d。有限元模型计算除本文1.3节取值参数外，25 m填筑体高度按场道工程压实度不同要求共分为 0.8，3.2 m 及 7 m×3 m 共计 9 层，其中道基层压实度根据现场工程检测数据并考虑机场工程压实要求，自上而下分别取值为96%和95%，剩余层取值为93%，并按式（1）反算为61.6，58.1 MPa及剩余的52.3 MPa压缩模量值。实测结果及有限元计算结果对比如表2所示。从表中可知，回填体本身压缩变形实测结果与有限元计算结果相差仅为2%，原地基沉降实测结果与有限元计算结果相差仅为5%，即本文的有限元模型计算填筑体沉降可靠性高。

表 2 有限元仿真结果与实测沉降对比Tab.2 Comparison of simulation and measured settlement

2.3.2 压实度–填筑体沉降的关系

为分析不同压实度下填筑体的沉降规律，采用有限元法计算7种压实度（85%，87.5%，90%，92.5%，95%，97.5%，100%）、8种填土高度（5，10，15，20，25，30，35，40 m）共 56 种工况下的沉降量，如图8所示。填筑体的沉降与填筑高度之间为指数幂关系，填筑高度越高，沉降越大。并且随着填筑高度的增大，填筑体沉降增速也在增大。这是因为填筑体中下部土体还需要承受上部土体的重力荷载，导致填筑体高度越高，下部土体受到的土压力越大；从填筑体顶面往下，土压力递增，下部土层对总沉降的贡献也递增。对比不同压实度下的沉降曲线发现，回填高度越高，压实度对土体沉降的影响越显著。为降低土体的沉降，施工期间应严格按照要求分层压实，严控土体的压实度。

由图8可知，土体沉降量S是填土高度h与压实度x的函数

为了确定式（2）的具体表达式，首先分析同一压实度时填土高度与沉降的关系。通过对上述曲线趋势分析，初步推测两者存在如下的指数幂关系

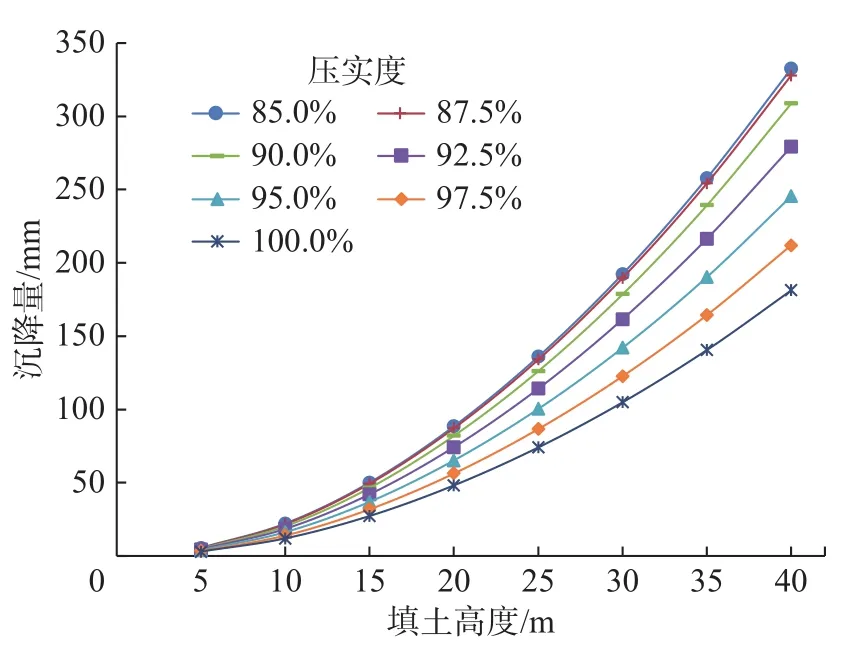
图 8 不同压实度下路基沉降量Fig. 8 Subgrade settlement under different compactness

式中：Sx为压实度x时的沉降量；a，b为待定参数。

通过拟合图8中的7条曲线得到式（3）的参数a和b，见表3。从表中发现，参数b的变化非常小，可视为常数，可取其均值（b=1.916）作为代表值。a的数值与压实度呈负相关关系，可表示为

式中，参数c～e通过拟合曲线拟合确定。将式（3）和式（4）代入式（2），即可得到土体沉降的多元回归公式

式（5）明确了压实度、填土高度与回填土体沉降量的关系，亦为高填方工程现场施工的沉降控制提供了简便的计算方法。

表 3 参数 a，b拟合结果Tab.3 Fitting results of a and b

为了验证原地基沉降预估模型式（5）的准确性，拟将该模型的预估值与有限元仿真值进行对比，如图9所示。分析中，压缩模量和填方高度重新随机设定。研究结果表明，原地基沉降与有限元仿真结果之间的误差不大于2.1%，进一步反映了原地基沉降的模型预估值与有限元仿真结果间的一一对应关系。

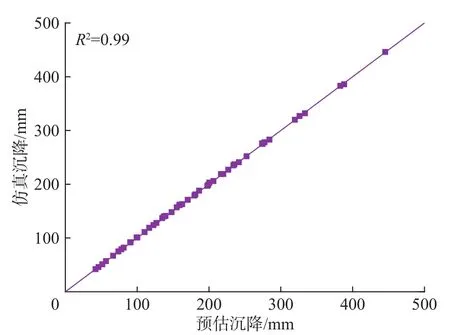
图 9 原地基沉降模型预估值与仿真结果对比图Fig.9 Comparison between the prediction values of original foundation settlement model and the simulation results

3 结束语

研究了我国中西部地区机场高填方工程粗粒土的压实度与压缩模量的关系，建立了粗粒土高填体沉降的简化计算方法。首先采用重型击实试验、压缩模量试验对由现场取回的粗粒土开展系统的试验研究；其次，结合试验结果，采用有限元法计算多种压实度、多种填筑高度下高填体的沉降量，以建立土体沉降的多元回归公式。根据试验结果，可得到以下结论：

a. 试验的所用填料属粗粒土，不均匀系数约为43.3，曲率系数为6.4，最佳含水率为6.2%，最大干密度为 2.13 g/cm3。

b. 压缩模量试验结果表明，粗粒土的压缩变形量与含水率呈正相关关系，并且其压实度与压缩模量具有良好的相关性。在此基础上，建立了该粗粒土压缩模量的预估方程，相关系数达0.96。

c. 基于有限元模型计算的填筑体沉降与实测沉降的误差为2%，说明该有限元模型的沉降计算较为可靠。

d. 填筑体的沉降与填筑高度为指数幂关系，填筑高度越高，填筑体的沉降越大，填筑体沉降的增速越大，土体压实度对沉降的影响越显著。

e. 基于有限元模型的沉降数据，明确了压实度–填筑高度–填筑体沉降的关系，建立了高填体沉降的多元回归方程，为高填方工程现场施工提供了简便的沉降计算方法。

基于现场取回的粗粒土开展压缩模量的研究工作，发现了压实度与压缩模量良好的相关性。受限于土体样本数，上述发现是否适用于其他土体仍需开展大量的试验验证。关于此方面的研究将在下一阶段开展。