“数形结合”思想在高中数学不等式求解中的应用
2020-11-20
一、数形结合思想概论
数学的起源就是古人研究的数形关系,数和形是数学研究的基本对象,其在某些条件下可以互相转换。在高中数学中,也是研究数形的关系,而数形结合就是数与形的关联。数形结合是一种数学思想,其有两种模式:一是使用数来阐述形的特点和属性,二是使用形来直观地表示数之间的关系。
在高中数学中运用数学思想的解题方法主要在三个方面。1.运用数形结合思想解决函数问题。2.运用数形结合方法解决不等式问题。3.运用数形结合解决平面几何问题。前两种都是用形来直观表示数之间关系的数形结合思想,第三种是使用数来阐述形的属性特点。
二、数形结合思想解决不等式问题
在不等式问题中运用数形结合来解答,可以避免复杂的分类讨论,简化题目,直接利用几何图形特点得出答案。
例题一:设有关于x的不等式|x-3|+|x-4|<a,若此不等式无解,求a的取值范围。
解:设函数f(x)=|x-3|+|x-4|,函数g(x)=a,在平面直角坐标系中作出函数f(x)和g(x)的图像如下。
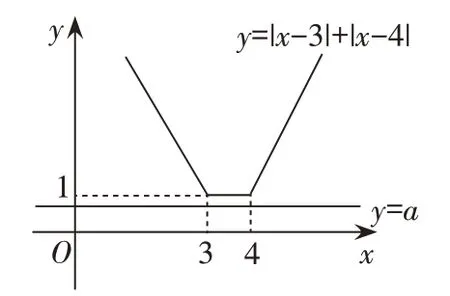
由函数f(x)和g(x)的图像特征可得要使|x-3|+|x-4|<a无解,只有使函数f(x)=|x-3|+|x-4|在函数g(x)=a的上方,或使函数g(x)=1。
所以可得a的取值范围为(-∞,1]。
例题二:设函数f(x)=x2-2ax+2,并且x∈[-1,+∞)时,f(x)≥a恒成立,求a的取值范围。
解:由f(x)≥a可得x2-2ax+2≥a即x2+2>a(2x+1)。
设函数f(x)=x2+2,函数g(x)=a(2x+1),作出函数f(x)和函数g(x)的图像:

由函数图像特征可得a的取值范围为图中直线斜率的取值范围。
即a∈(-3,1)。
三、数形结合思想解决平面解析几何问题
在高中数学中,平面解析几何知识是运用到数形结合思想最广泛的知识点,在直线斜率、直线与圆、直线与圆锥曲线等问题上,运用数形结合思想解题是最为简洁的。
例题一(直线斜率问题):直线L过点P(-1,2),且与点A(-2,-3)、B(4,0)为端点的线段AB相交,求直线L的斜率的取值范围。

在解这类题目时,先作出函数图形:
计算直线pa的斜率k(pa)=5,直线pb的斜率k(pb)=2/5。
由函数的图像特征可得k≥5 或k≤2/5。
例题二(直线与圆问题):设圆O的方程为x+y-2x+4y+4=0,直线L的方程为3x-4y+9=0,求圆O上的点P到直线L上的最大距离为多少。
在解这类问题时,运用数形结合思想能使问题得到迅速解决:
将圆的方程配方可得(x-1)2+(y+2)2=1,由此可得圆心O为(1,-2),半径r=1。
由直线与圆的图形特征可得:圆到直线的最大距离=圆心到直线的距离+半径。
圆心O到直线L的距离d=4,由上式可得直线L到圆O的最大距离为d+r=4+1=5。
