初中数学问题教学的思路探究

一、让数学问题在体验中解决，激发学习兴趣

为了培养学生的学习兴趣，调动学生的学习积极性，可以让学生亲自动手检验数学知识。学习简单而直接的问题，学生只是简单被动的接受，思考欲望会很低，甚至为零。如果能让学生实践操作，学生的积极性便会大大提高，解决问题的能力也会大大增强，对于知识的掌握也会更加牢固。

例如，在探究“最短路径问题”这一节课时，有这样一个问题：从线段A到线段C之间有很多条路可以选择，那么，从A点到C点怎样走路程最近呢？(如图1)问题的解决可以让学生到黑板上来操作，用细绳根据图中所示的路线进行测量并比较，最后看出连接A、C之间的直线是最短的，进而得出结论“两点之间线段最短”。当教师拿出细线问：“谁来到黑板前测量一下这几条线呢？”问题一提出，学生便仿佛脱离了课堂，并置身于实际生活中，因而迫不及待想寻找解决问题的办法，急于找出这一最短的路径。让学生动手实践操作，会极大调动学生学习的热情，不必说学生争先恐后地想到黑板上去演示，就是坐在下面观察的学生也会目不转睛，不放过任何一个细节。这样学到的知识记忆更加深刻，甚至会终生不忘。

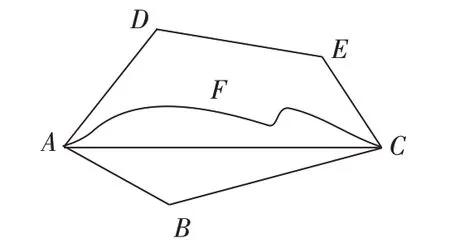
图1

二、把数学问题置于生活实践中，掌握问题规律

把数学知识运用于生活，创设问题情境，在生活中体现数学理念。问题情境的创设要充分考虑学生的认知、情感、性格、兴趣等多方面因素，问题的设计要贴近学生实际生活，将学生需要掌握的数学知识与现实生活紧密联系起来。只有在生活化的学习情境中去感知，才能使学生切实明白知识的价值，同时让学生在热情与挑战中探寻到数学问题的规律性。

设计这样的问题：某村在公路一侧有一菜园A，另有一深水井B，每年干旱季节都要对菜园进行人工浇灌，由于菜园在高坡地，需要在公路一侧安装一加压泵站M，那么泵站建在公路何处才能使从深水井到菜园铺设的水管最少呢？(如图2)

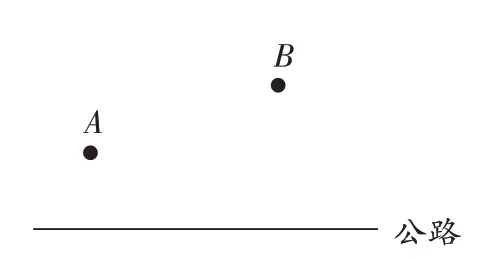
图2

图3

根据《课标》的要求，数学问题的设计既要保证问题的探索性，又要具备思维的延展性和形象的趣味性。把数学知识置于生活实际中，探索解决此问题的方法作为最终目标，为本节课埋下伏笔，设置悬念，激发学生解决问题的的主动性和战胜困难的挑战性。

回顾旧知，用“两点间线段最短”这一理论来解决这一问题，指引知识点的应用，打开学生思维的大门。接下来再引出与问题1 相似的问题：如果深水井A和菜园B在公路的两侧，那么在公路何处修建泵站所用管道最短呢？(如图3)依照刚才的思路，这个问题也会迎刃而解——连接AB交于公路一点M，那么就找到了泵站修建的位置。把到生活中寻找解决问题的方法作为这节课的目标，使学生在轻松愉悦的氛围中积极主动地探索数学的奥妙，并找到数学的规律。

三、让数学问题在探究中生成，提升总结能力

数学知识不是单一的孤立存在的，知识的输入要注重知识的发生、发展过程，问题的设计要适宜改变，体现过程变式教学策略。进阶式引向深入，提升学生多角度理解问题的能力，引导他们对教学内容的主动建构和有效迁移。运用学过的知识不断进行探究，不仅会激发学习的兴趣，还会提升解决问题的能力。

为解决本节图2 的问题，可以再设计这样的问题进行探究：如果在公路两侧都有一口深水井B和B′，并且关于公路对称，我们尝试连接AB′，交公路于点M，比较一下AM+MB与AB′的数量关系，会有什么发现？(如图4)

通过教师思维引导，学生的积极探索，不仅发现了AM+MB与AB′的数量关系，而且探究总结出关于对称图形的几个性质，结合合图3 和图4 的思路，找到了解决图2 问题的解决方案，从而达到本节的教学目标。通过探究，可以找到问题的实质，让学生在探究中发现规律，提高总结问题的能力。

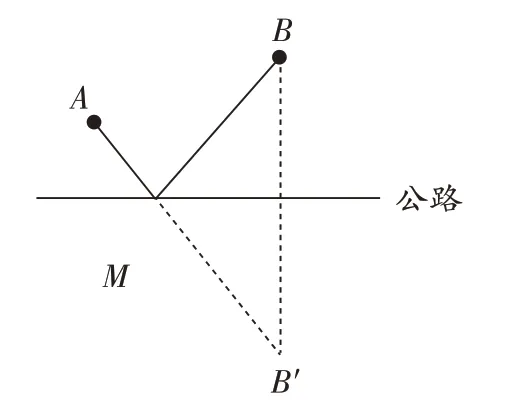
图4

问题教学是数学研究的出发点，是引导学生学习数学的一把钥匙。因此，在课堂教学中要注重数学问题的提出与解决，要充分体现学科核心素养中彰显学生主体地位的核心理念，让学生在数学学习的道路上越走越宽。