小学生数学学习偏差认知转变的教学策略研究
2020-11-20江苏无锡市春城实验小学王炎萍钱科英
江苏无锡市春城实验小学 王炎萍 钱科英
在小学数学学习过程中,学生往往绕不开错误一词。儿童在出错、纠错、顿悟中理解数学知识、发展数学思考,“错误”是学生学习中挥之不去的一个部分。在针对学生的错误开展的教学研究中,“偏差认知”是一个独特的视角,研究小学生数学学习偏差认知转变的有效教学策略是一个有价值的课题。关于偏差认知转变的教学策略研究,以往的研究多倾向于发现已存在的偏差认知,探讨如何转变,这类补救型的教学策略较为被动。而现有的针对数学课堂的教学研究,重心大多为学生在哪些知识上存在偏差认知及偏差认知为何难以解决,缺乏对偏差认知自然属性的归因探究。本文遵循“学生的偏差认知有何自然属性,可以采取什么有效教学策略”的正向思维,探索偏差认知心理层面存在的可能倾向,在此基础上探索应对策略。
一、机械识记下的偏差认知,培养意义识记
机械识记适用于低年级的学生,一旦学习材料变复杂,学生在机械识记时就会产生偏差认知,这也就是意义识记的培养不可替代的原因。儿童的认知规律告诉我们,只有那些被他们理解的、系统的知识,才能更长久地保留在记忆中,并在需要的时候很快地提出“内存”,即意义识记。在小学数学教学中,培养意义识记的策略是帮助学生在头脑中建立所学内容的多方联系,以理解为前提,使之系统化,从而有效控制偏差认知的形成。
【案例1】“解决问题的策略——假设”教学片段
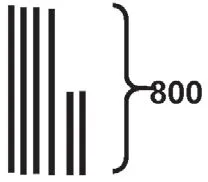
出示: 去世博园参观,王老师用800元钱买了4张普通票和两张优惠票,已知每张普通票的价钱是优惠票的两倍。每张普通票和优惠票各多少元?
要求:尝试将题意用画图的方式表示出来,然后小组讨论。
展示:经过集体交流,采纳右图。
(讨论片段)
师:先来说说你画的图表示什么意思?
师:我们怎么才能知道画的图是不是正确呢?
生1:将题目条件标注。
生2:对照图形能将题目意思大致说出来就行。
师:两个量是2倍时可以从线段长短大致看出来,要是3倍或者4倍怎么办呢?
生:那就需要标注。
师:“线段”多了怎么办?
生:可以用省略号表示。
师:你能根据图形说说你的解题思路吗?
……
爱因斯坦曾说:忘掉学校所学的一切知识,剩下的才是教育。教材例题虽然呈现了实物图,但实物图只能帮助学生理解假设的过程,要想真正地解决问题,还需要数形结合实现意义建构。这样的思路简析图便于将问题情境数学化,学生看着图就能在脑海里建构出整个题目的框架。值得注意的是,画图应顺应学生的思维,能表征问题的同时,还能帮助分析数量关系,解决相应的实际问题。另外,将多样化的画图方法进行最优处理也值得重视,即引导学生归纳概括出解决一类问题的通用模型图。这样的意义教学,学生不仅能理解知识背后的方法与思路,还能为接下来的学习之路打下坚实的基础。相信经历过意义识记的学生产生偏差认知的可能性会降低,学习效果会更好。
二、注意失调下的偏差认知,培养有意注意
注意可分为无意注意、有意注意和有意后注意三种,无意注意和有意后注意都是不需要意志努力就能产生的注意;而有意注意,是人所特有的一种心理现象,它是有目的、需要一定意志努力的注意。在实际的教学中,组织好学生的有意注意是教学成功的一个重要因素。但由于小学生受年龄特点、生理条件等影响,有意注意一般持续时间短,维持比较难,因此在学习中容易受到干扰,导致学习效率降低。由此可见学生要提高解题能力、规避偏差认知,那就要培养有意注意。而课前3分钟的准备环节正是培养有意注意的好时机。
【案例2】在学习因数和倍数这一内容时,笔者在课前3分钟组织学生玩起了“报数游戏”的比赛。比赛规则:每人每次按自然数的顺序报数,最少可以报1个自然数,最多可以报3个自然数,比如甲报1、2;乙可以报3或3、4或3、4、5。谁先报到100,谁就获胜。显而易见,这场比赛极具挑战性和刺激性,能激起学生浓厚的兴致和热情,在玩的过程中学生主动思考赢的秘诀,探索其中的规律。玩这样的游戏,学生的思维专注又深刻,并且他们带着饱满的精神和良好的体验进入新课学习,课堂教学效率也得到了相应的提高,有效避免了注意力缺失造成的偏差认知的产生。
三、思维定式下的偏差认知,培养创造思维
在环境不变的条件下,定式能发挥积极作用,使人快速准确地解决问题。而当情境发生变化时,它反而会阻碍新方法、新思路的诞生,从而出现偏差认知,也就是思维定式的消极作用。为了帮助学生克服思维定式、培养创造思维,我们可以从数学知识的本质内涵入手,培养学生仔细审题的习惯;或修改题中条件,使学生从具体问题、具体情境处着眼,转换思考角度,突破思维定式的瓶颈,激发他们的创造思维。
【案例3】如图,大正方形的边长是8厘米,求圆的面积。
这是一道常规题,在教学时,笔者保留了原图,分别修改了问题和条件,让看上去眼熟实际上却不一样的题来帮助学生走出偏差认知的误区。
(1)大正方形的边长是8厘米,求圆里面小正方形的面积。
(2)已知大正方形的面积是24平方厘米,求这个圆的面积。
受思维定式的影响,很多学生求第(1)问时,误把小正方形的边长当作圆的半径。经过教师的点拨,学生立即发现自己上当了,实际上,只要把小正方形的两条对角线相连,就能发现小正方形的面积等于大正方形面积的一半。这题让学生明白看题目要仔细审题,从问题出发分析解决问题的突破口,避免习惯性上当。
在解决第(2)问时,更多的学生为难了:不知道半径,怎么求面积?通过画图可以发现,把大正方形平均分成四个小正方形,每个小正方形的面积就是r×r=6平方厘米,这样圆的面积S=πr²=3.14×6=18.84平方厘米,问题就迎刃而解了。换一个角度,圆面积S=πr²,如果r没法求,知道r²一样可以解决问题。解决方式不同,但本质却一致,都是从圆面积公式出发。
人一旦走出思维定式,很多奇迹就会发生。从飞鸟可以造出飞机,从蛋壳想到了薄壳建筑,从苹果落地可以悟出万有引力定律……一旦走出思维定式的消极影响,那么思维必定变得缜密,向着更广、更深的方向发展,从而帮助学生产生“抗体”,自觉走出偏差认知的误区。
四、聚合思维下的偏差认知,培养思维品质
为了避开偏差认知,让小学生正确、快速地回答问题,我们可以从根源思考,培养学生良好的思维品质。思维品质的培养可以着力于练习的设计,通过有目的地设计“一题多解”和“变式练习”题,逐步锻炼学生思维的逻辑性、广阔性、独立性、灵活性、批判性等。
【案例4】“解决问题的策略——转化”教学片段
师:请同学们仔细观察这个算式有什么特点。
生:我发现后一个分数总是前一个分数的一半。
师:用什么方法可以求它们的和呢?
生1:可以先通分,转化成同分母分数再求和。
生2:我觉得也可以转化成小数再求和,因为这些分数的值都是有限小数。
师:说得很好,还有不同的方法吗?
(生有点疑惑,教师适当引导,比如结合画图来思考)
生:可以画图来思考,先画一个大正方形表示单位1,如图。从图中可以直观地看出:

……
当学生的思维处在瓶颈处时,教师不妨伸出援助之手,让学生在前行中感受来自教师和同伴的帮助,感受学习成功的内在满足感和自豪感。通过多种办法解决这个题目,不仅让学生领悟到低头沉思的动人之处,也让他们感受到抬头仰望极限思想、数形结合思想的无穷魅力,更为学生解题方法的创新提供了可能。经过这样长期的训练,学生的思维会趋于严谨、更有逻辑性和条理性,偏差认知的出现概率会大大降低。总之,练习的设计不可局限于一个问题的解决,而要关注问题解决过程中的数学知识及思想方法,更要关注学生在解决问题中数学素养的形成。
基于学生认知心理层面展开的关于偏差认知教学策略的研究,是在教学中遵循学生天性、重视学生学情、关注学生“道理”的重要体现,也是培养学生数学核心素养的有力支撑。
