探讨粒子数密度问题培养学生科学思维
2020-11-19周金学
周金学
一、问题的提出
近几年,浙江省的物理选考试卷中多次出现了群发粒子在磁场中运动的题型,有学生提出:什么情况下粒子经磁场偏转后分布均匀,什么情况下分布不均匀?笔者首先引导学生将问题梳理,常见群发粒子有:1、发射速度方向恒定但大小不同,且包含了一定区间范围的所有速率的同种粒子;2、发射速度大小恒定,方向在一定角度范围内的同种粒子。粒子经磁场后分布是否均匀涉及的是三种常见数密度:1、速密度指单位速度范围内的粒子数,2、线密度指单位长度范围内的粒子数,3、角密度指单位弧度范围内的粒子数。
二、例析粒子速密度和线密度的关系
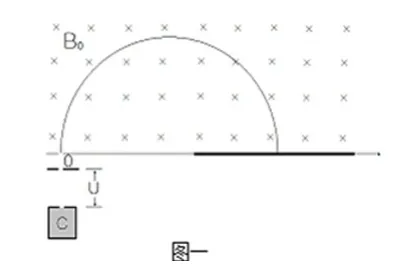
粒子源发射速度方向恒定而大小不同的粒子,经磁场偏转后其散布均匀与否因落点平面不同而不同。2016年浙江省物理选考23题以质谱仪为基础考查了粒子偏转后的分布问题,如图一所示,此题为减小难度,直接给出了条件:打到x轴上的离子数均匀分布(离子重力不计)。下面分析质谱仪的粒子源具备什么条件才能使打到x轴上的粒子能均匀分布。简化如下模型:在x轴的上方存在垂直纸面向里,磁感应强度大小为B0的匀强磁场,离子源C发射质量为m、电荷量为q的一束负离子,其初速度大小范围为0~v0,从小孔O(坐标原点)垂直x轴并垂直磁场射入磁场区域,最后打到x轴上的水平固定探测板上。
设某粒子速率为v,则其落点与O的跨度为,另一粒子速率为v+Δv,则其跨度为,两粒子间距为Δ。设单位长度内粒子数为Δn,打到x轴上的离子数均匀分布,则其线密度也为常数,即粒子源发射的粒子速密度恒定则收集板上粒子的线密度也恒定。
归纳推理是从个别(特殊)事物到普遍(一般)事物的逻辑推理方法,以上结论还能归纳出更普遍的规律:若粒子发射速度方向恒定而大小不同,只要在匀强磁场中轨迹所对圆心角相同,则落点粒子线密度与发射粒子速密度成正比。证明如下:如图二直角三角形OMN区域中存在一匀强磁场,从O点沿OM发射速率各不相同的同种粒子(不计重力),分别从ON边上射出,设OA1轨迹对应粒子速度为v,OA2轨迹对应粒子速度为v+Δv。易证OA1和OA2弧度相等,则,若速密度为定值,可得,即线密度也为定值。

但磁场中粒子轨迹所对圆心角不同,则粒子落点线密度与发射速密度不成正比,如条形有界磁场的情况。如图三所示,在两平行板间存在匀强磁场,若O点发射的粒子速度方向始终垂直于极板而速度大小不同,则粒子在磁场内的轨迹圆弧所对圆心角依次减小。若粒子源速密度恒定,假设粒子能运动至AC段,则在AC段的线密度相同。假设,因此MN段的粒子线密度大于NB段。

三、例析粒子角密度和线密度的关系
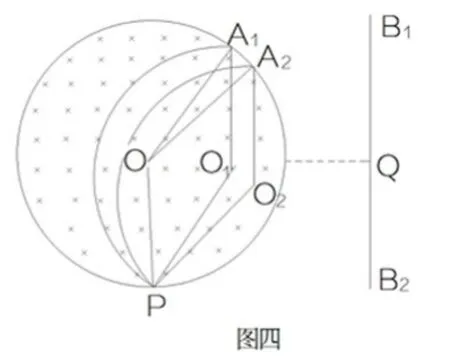
下面分析粒子源发射速度大小恒定而方向各异的粒子,经磁场偏转后其散布密度特征。如图四所示为一类平面聚焦磁场,在半径为R的圆形区域内有匀强磁场,P点处有一粒子源,向磁场内各个方向发射速率为v(v=)的粒子,且粒子的角密度恒定,则粒子从磁场圆弧边界飞出时,线密度也恒定。证明如下:PA1轨迹和PA2轨迹粒子的发射角度相差Δθ,易证∠A1OA2和∠O1PO2都为Δθ,则圆弧A1A2=Δx=ΔθR,若P点的粒子角密度为定值=Rk也为定值。粒子离开圆形磁场后形成平行粒子束,若垂直打在收集板上,则在收集板上的线密度就不均匀了,从Q点向两边线密度逐渐增大。若收集板B1QB2是与圆形磁场半径相同的圆弧,则能保持线密度均匀。
四、结语
学生的问题是其“最近发展区”,对其深入挖掘不光能解决学生的疑惑,更能在问题解决的过程中发展学生的核心能力。思维是人脑对客观事物的认识过程,总是以一定的形式、方法和程序进行的[2]。本问题的研究中学生经历了提出问题,构建模型,分析推理,数学论证的科学思维历程,提高了创新能力,理解能力、分析综合能力、应用数学解决物理问题的能力。帮助学生形成从物理学角度解释客观事物的本质属性、内在规律和相互关系的能力,对学生实践创新素养的形成起到了积极的作用。
