高铁可达性、空间溢出效应与制造业集聚

朱文涛，顾乃华

(1.集美大学 财经学院，福建 厦门 361021；2.暨南大学 产业经济研究院，广东 广州 510632)

一、问题提出

交通基础设施建设带来的运输成本节约，被认为是影响经济活动的重要因素。2008年以来，中国进行了大规模的高铁建设投资，每年均有新增的高铁客运专线通车运营。截至2017年底，高铁营业里程已达到2.5万千米，占到全球高铁营业总里程的65%。尽管国内外学者已开始基于中国案例考察高铁开通的经济和社会影响，但目前的研究大多停留在考察是否开通高铁对本地经济活动的影响，高铁的空间溢出效应却很少涉及。然而，高铁作为一项重要交通基础设施，具有很强的网络外部性特征[1-3]。一个城市开通高铁，可能不仅会对本地经济活动产生影响，还会通过空间溢出效应影响周边地区的经济活动。如果忽略了高铁溢出效应，将很难准确度量高铁的经济效应。

改革开放40年来，中国各地区制造业都获得了较大程度的发展，但空间分布极不平衡。制造业高度集中于中心城市和经济发达的东部沿海地区，而非中心城市和经济欠发达的内陆地区，则普遍面临着制造业份额偏低、集聚效应和规模效应无法充分实现的发展困境。制造业发展的空间失衡，带来的经济发展差距持续扩大，已成为制约中国经济高质量发展的重要因素，在推进中国经济由高速增长向高质量发展、实现经济发展动能转换过程中，必须更为关注制造业的协调发展问题。在此背景下，考察高铁大规模通车带来的城市可达性改善到底是进一步加剧了制造业发展的空间失衡，还是有助于促进区域间制造业协调发展具有重要的现实意义。实际上，高铁通车对所在城市而言，最为直观的作用体现在铁路提速促使该城市与其他城市之间在旅行时间上的极大节约。旅行时间节约带来的可达性条件改善改变了城市的区位条件，进而影响制造业在不同城市的集聚。基于这种考虑，本文以高铁可达性为切入点，以66个具有铁路客运站点的非中心城市为考察样本，在测算城市之间的铁路旅行时间基础上，构造反映城市高铁可达性的相关指标，实证分析高铁开通带来的可达性变迁对非中心城市制造业集聚的本地影响及空间溢出效应，进而从侧面验证高铁在区域间制造业协调发展中所发挥的作用。

二、文献回顾

进入21世纪后，有关交通基础设施对制造业集聚影响的实证研究文献日益增多，近年来一些文献已开始从可达性视角，考察交通基础设施对制造业区位的影响。如阿劳素-卡罗德和阿拉尼翁-帕尔多(Arauzo-Carod & Alaón-Pardo，2009)分析了交通可达性改善对制造业企业区位的影响，发现路网改善在工业区位决策中发挥着重要作用，更高的可达性意味着更低的旅行成本，使外部规模经济更加可行，从而有助于集聚[4]。宋等人(Song et al.，2012)研究了首尔都市圈的产业集聚与交通可达性之间的关系，认为尽管首尔大都市地区迅速扩张，但中心商业区仍然是工业和运输系统的中心，大多数工业子行业均在中心区域集聚，而只有初级制造业集聚不在中心区域，总体而言，运输网络与产业集聚呈正相关关系[5]。于等人(Yu et al.，2016)基于中国274个城市2000—2010年面板数据，探讨高速公路网络在空间经济集聚演化中的作用，发现高速公路网络的改善带来的区域可达性改善导致经济活动的地理集中程度更高。西部地区高速公路网络对经济集聚的影响是负向的，这意味着中国欠发达地区会由于道路可达性的增加而变得更加边缘化[6]。另外，一些学者针对不同国家的研究也发现交通可达性改善对制造业区位具有重要影响[7-9]。从国内文献来看，少数学者从可达性角度考察交通基础设施对制造业企业区位的影响[10-11]。以上文献多是以公路基础设施作为研究对象，对铁路设施带来可达性改善的集聚效应考察则较少。

近年来，随着高铁在全球范围内的兴起，有关高铁对制造业集聚的影响也日益引起学者的关注，但对于高铁是否促进了制造业集聚以及高铁促进制造业在中心城市还是沿线非中心城市集聚，仍然存在争议。一项基于荷兰的研究发现高速铁路会影响企业选址，高铁列车服务可以改变区位，对企业区位选择有重要影响[12]。孙等人(Sun et al.，2017)[13]和戴等人(Dai et al.，2018)[14]也有类似发现。国内文献方面，王鹏和李彦(2018)利用双重差分法估计高铁对城市群经济集聚演变的影响，发现高铁建设有助于城市群集聚经济梯度效应的实现，整体上看高铁促进了长三角城市群制造业的扩散和生产性服务业集聚[15]。李雪松和孙博文(2017)以京广高铁沿线城市为样本，在构建内生运输成本和工资对制造业集聚决定模型基础上，分析高铁开通对站点城市制造业集聚的影响，其研究发现高铁开通对站点城市制造业集聚效应将逐渐经历集聚加速、集聚弱化以及扩散阶段，高铁开通普遍提高了站点城市制造业集聚水平，对中心城市制造业集聚的影响处于集聚弱化阶段，而对非中心城市的影响处于集聚加速阶段[16]。卢福财和詹先志(2017)研究发现开通高铁对工业企业集聚程度的提高具有显著的拉动作用，这种拉动作用会随着高铁数量的增加而加强，高铁对人口规模小于50万城市制造业集聚影响最为显著[17]。

从现有文献来看，有关高铁的制造业集聚效应研究，主要存在以下几点不足：一是主要采用双重差分法考察是否开通高铁对本地制造业集聚的影响，虽然双重差分法能够部分克服高铁建设的内生性问题，但虚拟变量的设置方法在估计高铁边际影响方面具有较强的局限性；二是忽略了高铁和制造业集聚在地理空间上的依赖性和空间溢出效应，高铁的网络属性和区域间经济互动的加强，使得经济活动普遍存在空间互动特征，忽略了空间因素，可能会低估高铁发展对制造业集聚的影响。

相比于已有的文献，本研究的创新点主要体现在以下几个方面：一是将人文地理学中的可达性概念应用到高铁影响制造业集聚的研究中，侧重从可达性角度探讨高铁发展带来的城市可达性改善对制造业集聚的影响，而从这个角度切入的国内文献较为少见，本文的研究有助于拓展现有的研究；二是本文考虑了高铁的空间溢出效应，采用空间杜宾模型考察高铁可达性及溢出效应对制造业集聚的影响，克服了传统估计方法中忽略空间互动可能导致低估高铁集聚效应的不足。此外，本文的创新还体现在空间权重设置方面，以往的研究文献多通过构造邻接权重、地理距离权重估计空间计量模型，考察本地交通设施对周边地区的溢出效应。一般认为溢出效应随地理距离的扩大而呈现递减特征，但实际上溢出效应随距离衰减的速率也会受到地区间经济发展差异性及制度质量异质性的影响。基于这点考虑，本文在构造空间权重过程中，除构造传统的地理距离权重外，还构造了经济地理复合权重和制度距离复合权重，能够更为真实地反映距离衰减效应外，也保证了结果的稳健性，弥补一些研究文献中忽略地区制度质量异质性和经济发展差异性对距离衰减速率影响的不足之处。

三、变量、数据与模型

(一)变量选取与数据说明

借鉴孙等人(2017)[13]和绍等人(Shao et al.，2017)[18]的做法，本文用区位熵(LQit)作为衡量城市制造业集聚的指标，区位熵具体计算公式为：

(1)

其中，Muemployit表示城市i在t时期的制造业就业人数，Employit表示城市i在t时期的就业人数，Muemployall,t表示在t时期的全国制造业就业人数，Employall,t表示在t时期的全国总就业人数。

1.核心解释变量

本文选取的核心解释变量为高铁可达性，借鉴陈和海恩斯(Chen & Haynes，2017)[19]类似的方法，本文分别构造了日常可达性系数和可达性潜力作为城市高铁可达性的衡量指标。说明如下：

(1)日常可达性系数。该指标衡量了城市旅客通过铁路运输系统在一定的时限范围内可以到达城市数量的机会，借鉴陈和海恩斯(2017)[19]的研究，本文将时间设定为4小时，4小时通常被认为可以进行舒适一日游的时间。采用日常可达性系数作为城市高铁可达性的第一个替代变量，具体计算公式如下：

(2)

其中，Popj为城市j的人口数量，γij为时间阀值。如果城市i到城市j的旅行时间大于4小时，设γij=0；小于4小时，则设γij=1。

(2)可达性潜力。该指标是对城市接近市场可能性的一种度量。经济地理学认为城市之间的相互引力与市场规模呈正比，与城市间距离成反比，将城市间距离用铁路旅行时间加以替代，作为城市高铁可达性的另一替代变量，可达性潜力的公式如下:

(3)

其中，GDPj,t为j城市在t时期的国内生产总值，Timeij,t为t时期城市i到城市j的铁路旅行时间。

2.控制变量

为了减少遗漏变量造成的估计偏误，本文加入人力资本(eduit)、产业结构(indusit)和政府支出强度(govit)等代表城市特征的控制变量。其中，人力资本采用万人中在校大学生人数表示，也即人力资本=在校大学生人数/地区年末总人口；产业结构采用第三产业从业人员比重表示，也即产业结构=第三产业从业人员数/年末单位从业人员数；政府支出强度采用每单位国土面积财政支出规模表示，也即政府支出强度=(地方财政一般预算内支出-科技支出-教育支出)/行政区划面积。

3.数据来源

本文数据来源于以下数据库：一是国家统计局公布的2006—2013年《工业企业数据库》。该数据库涵盖中国规模以上所有国有和非国有工业企业数据。由于本文考察对象是制造业，因此剔除了工业企业数据库中非制造业企业样本，仅保留制造业企业样本，剔除行政区划代码缺失、从业人数小于10的企业样本，并参考中国民政部网站公布的各年度县级以上行政代码，对企业所对应的行政代码进行匹配。针对考察期内发生的国民行业分类标准变更情况，在进行分行业的区位熵计算时，通过行业分类转换表(1)限于篇幅未列出行业分类转换表，备索。，统一两者的差异，保证数据的连贯性和可比性。二是铁道出版社、北京极品时刻科技有限公司出版的《极品列车时刻表》。采用站站查询的方法，通过输入两个城市站点，获得两城市站点的最短列车旅行时间；三是EPS全球统计数据及分析平台中的中国城市数据库，该数据库包含中国城市层级的经济数据，按照数据类型分为市辖区和全市数据。本文所有指标均采用全市数据。选取的数据时间段为2006—2013年，以66个外围城市共528个样本为考察对象(2)66个地级城市包括：唐山、秦皇岛、邯郸、邢台、保定、沧州、廊坊、阳泉、锦州、辽阳、盘锦、铁岭、葫芦岛、吉林、四平、无锡、徐州、常州、苏州、镇江、温州、嘉兴、绍兴、衢州、蚌埠、淮南、鞍山、滁州、宿州、六安、泉州、漳州、萍乡、九江、新余、鹰潭、宜春、上饶、淄博、枣庄、潍坊、泰安、德州、开封、洛阳、安阳、鹤壁、新乡、许昌、漯河、三门峡、商丘、信阳、驻马店、黄石、十堰、宜昌、襄阳、孝感、咸宁、随州、韶关、东莞、南充、宝鸡、渭南。这些城市在不同年份中相继开通高铁，部分城市即使未开通高铁，也能通过中转方式获得高铁的溢出效应。。

(二)空间权重与空间相关性诊断

在进行空间计量分析之前必须对各变量的空间相关性进行检验，借鉴多数文献的做法，采用莫兰指数(Moran’sI)对各变量空间相关性进行检验，莫兰指数的具体计算公式为：

(4)

空间权重矩阵Wij的设置无论对于空间相关性检验还是空间计量估计均十分关键，本文通过设置以下多种空间权重来确保实证结果的稳健性：

(1)地理距离权重(W1)。选择较为常用的地理距离倒数平方来构造地理距离权重(3)两个城市间地理距离测算是以城市的政府所在地经纬度为基础，通过R软件测算城市政府所在地之间的球面距离得到的。，具体公式为：

(5)

(2)经济地理复合权重(W2)。城市间的关联效应不仅体现为随地理距离增加而衰减，还可能表现为经济发展水平较高的城市对周边城市的影响和辐射作用更强。本文借鉴李婧等(2010)[20]的做法构建以下经济地理复合权重：

(6)

3.制度地理复合权重(W3)。除了构建地理距离权重和经济地理距离复合权重外，本文还构造了基于制度地理距离的空间权重。由于历史、文化和经济原因，中国不同地区制度质量仍然存在明显的差异。处于转型期的中国，各地区市场化进程并不一致。制度环境越为相近的地区，要素流动所面临的制度摩擦越小。基于这种考虑，本文在地理距离权重基础上，进一步构造以下制度地理距离复合权重矩阵：

(7)

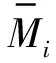
可以看出计算制度距离的关键在于测算城市的制度质量。然而，制度质量的测算是比较困难的。鉴于已有的研究文献较多基于市场化水平来测度地区制度质量，本文也侧重从市场化角度测算地区制度质量。借鉴王小鲁等(2016)[21]构造市场化制度的方法，选取资源配置的市场化、非国有经济发展、产权保护程度和经济开放度等分项指标基础上，运用主成分分析法测算考察期内各城市的制度质量。具体地，采用政府支出占GDP比重衡量资源配置的市场化程度(x1),该指标越小说明资源配置的市场化程度越高；采用城镇私营和个体从业人员数占城镇就业总人数比重衡量非国有经济发展状况(x2),该指标越大说明非国有经济发展越好，市场化程度越高；采用人均专利申请授权数衡量地区产权保护程度(x3)，该指标越大表示产权受到保护的程度越高，该分项指标数据来源于专利云数据库；采用工业总产值中外资和港澳台企业产值比重(x4)以及外商直接投资占GDP比重(x5)衡量经济开放程度，该指标越大说明地区开放程度越高。借鉴王小鲁等(2016)[21]的做法分别采用式(8)对各分项指标进行线性标准化计算：

(8)

其中，Wk为某城市第k个指标的原始数据，Wmax是与所有考察的城市第k项指标相对应的原始数据最大值，Wmin为第k项指标相对应的原始数据最小值。为了使各年份指数具有可比性，采用式(9)计算t年的第k项指数：

(9)

其中，Wmax(1)表示k项指标在基期的最大值，Wmin(1)为k项指标在基期的最小值。在进行线性标准化后，通过主成分分析法，确定各分项指标权重。本文所选定的权重为上述各指数评分值序列第一主成分特征值。权重用Wi表示，衡量制度质量的综合指数如下：

insit=w1Z1+w2Z2+w3Z3+w4Z4+w5Z5

(10)

基于以上三种空间权重矩阵，本文测算被解释变量和核心解释变量在2006—2013年的全局莫兰指数值，具体如表1所示。可以看出三种不同权重的莫兰指数均在0～1之间，且均在1%的水平上显著，各变量表现出明显的空间正相关性。

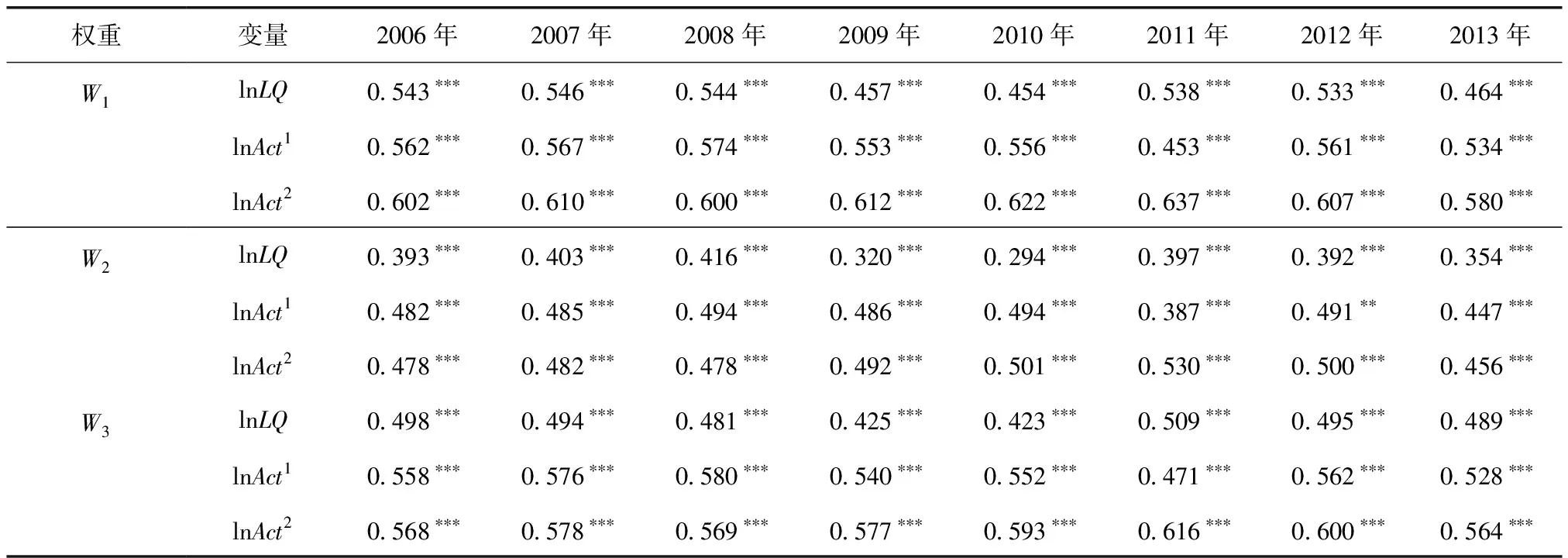
表1 2006—2013年主要变量的莫兰指数

(三)空间杜宾模型的设定

空间相关性检验表明应将传统计量模型拓展为包含空间关联效应的空间计量模型。本文采用空间杜宾模型对高铁可达性的溢出效应进行估计，空间杜宾模型(SDM)的一般表达式为：

Yt=δWYt+αlIN+Xtβ+WθXt+ε

(11)

其中,Yt为被解释变量的列向量，W为空间权重矩阵，Xt为解释变量矩阵，αl为常数项，IN为单位矩阵，δWYt为被解释变量的空间滞后项，表示来自其他空间单元被解释变量对本地区被解释变量的溢出效应，WθXt表示来自其他空间单元解释变量对本地区解释变量的影响。δ、β和θ为待估参数，ε为随机误差项。如果θ=0，则空间杜宾模型将退化为空间自回归模型(SAR)：

Yt=δWYt+αlIN+Xtβ+ε

(12)

而如果θ=δβ，则空间杜宾模型将退化为空间误差模型(SEM):

Yt=αlIN+Xtβ+u

(13)

u=λWu+ε,如果θ+δβ=0，则有λ=δ

莱萨热和佩斯(Lesage & Pace，2009)[22]认为使用点估计检验空间溢出效应，可能会出现模型估计偏误问题。为了更为准确地估计空间溢出效应，必须借助于偏导数的方法，将总效应分解为直接效应和间接效应。具体地，可以将式(11)转换为以下形式：

Yt=(1-δW)-1αlIN+(1-δW)-1(Xtβ+WXtθ)+(1-δW)-1ε

(14)

运用式(14)对解释变量求偏导数可以得到：

(15)

式(15)最右端矩阵中对角线系数为直接效应，表示解释变量对本地被解释变量的直接影响，非对角线系数为间接效应，表示其他地区解释变量对本地区被解释变量的空间溢出效应。以上仅给出了空间杜宾模型的一般形式，结合本文的研究实际，用于实证分析的空间杜宾模型具体形式如下：

(16)

四、实证分析

(一)模型选择及空间杜宾模型估计

本文利用贝洛蒂等(Belotti et al.，2013)[23]提供的xsmle程序进行空间杜宾模型估计，从稳健性出发，采用地理距离、经济地理距离和制度地理距离空间权重进行估计。表2报告了基于MLE估计的空间杜宾模型回归结果。在处理空间面板数据时，需要确定哪种模型对样本的解释力更强。表2下半部分报告了有关空间计量模型选择的各种检验结果。具体地，本文通过以下一系列检验，验证空间杜宾模型相比于其他空间模型的优势及确定模型的最优形式：首先，通过豪斯曼(Hausman)检验对采用随机效应还是固定效应进行判断，三种空间权重下的检验结果均拒绝了采用随机效应的原假设，说明采用固定效应模型更为合适；其次，通过伍尔德(Wald)空间滞后检验判断θ=0是否成立，也即判断SDM模型是否可以简化为SAR模型，检验结果均拒绝了SDM模型可以简化为SAR模型的原假设；本文进一步通过LR空间误差检验判断θ+δβ=0是否成立，也即检验SDM模型是否可以简化为SEM模型，检验结果拒绝了SDM可以简化为SEM的原假设。进一步，本文通过对比AIC和BIC值在SAC和SDM模型进行选择，检验结果表明加入误差项后并没有使AIC和BIC值变小，说明相比于SAC模型，SDM模型更为合适。通过以上步骤，可以认为采用SDM模型是合适的。另外，SDM模型包含无固定效应、时间固定效应、空间固定效应和时空固定效应四种。本文主要通过比较LogL、Sigma2和R2的值大小进行判断，最终选择包含时间固定效应的SDM模型作为实证分析的基准模型。

表2各列报告基于不同权重的估计结果。表2列(1)和列(2)报告基于地理距离权重的空间杜宾模型估计结果；列(3)和列(4)报告基于经济地理距离权重估计的空间杜宾模型回归结果；列(5)和列(6)报告基于制度地理距离权重估计的空间杜宾模型回归结果。可以从表2的回归结果对城市高铁可达性与制造业集聚之间的关系进行初步判断，莱萨热和佩斯(2009)[22]认为使用点估计检验空间溢出效应可能会出现模型估计偏误问题，有必要借助偏微分方法，将总效应分解为直接效应和间接效应两部分。从表2的回归结果来看，各列回归结果中各可达性变量的系数均显著为正，但从各空间滞后项来看，两个可达性变量的空间滞后项系数的显著性却存在一定差异。为避免点估计检验空间溢出效应可能出现的模型估计偏误问题，本文借助偏微分方法，将总效应分解为直接效应和间接效应，表3报告了总效应分解为直接效应和间接效应的结果。

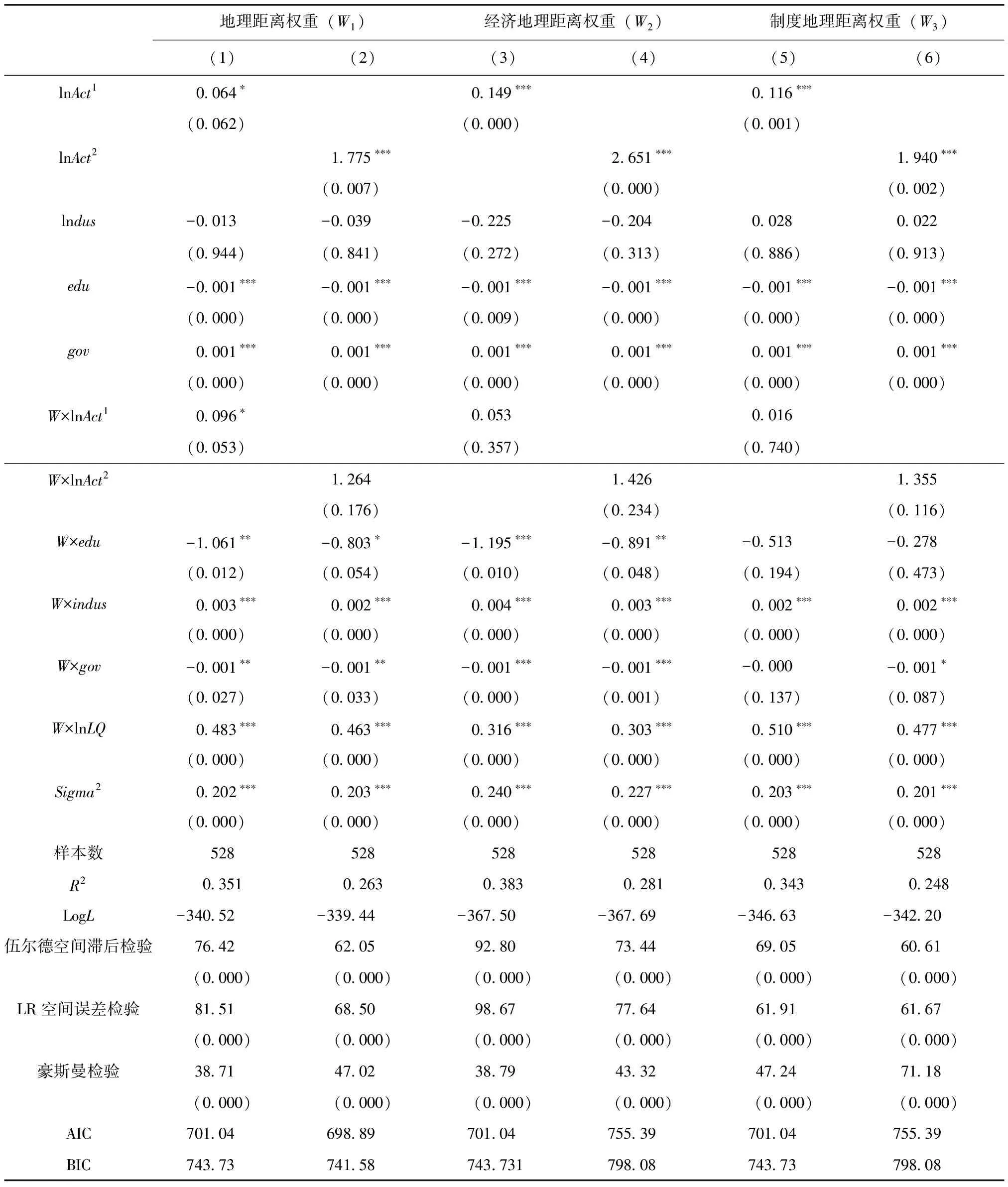
表2 不同空间权重下的SDM模型回归结果

(二)直接效应与间接效应

1.直接效应

直接效应也即本地效应，表3报告了三种空间权重下的直接效应估计结果。可以看出三种空间权重下，两个可达性变量的系数均为正，且均至少在5%水平上显著，说明高铁带来的城市可达性水平的改善有助于提高本地区制造业集聚水平。可达性改善之所以有助于本地区制造业集聚水平的提高，可以从要素市场和产品市场两方面解释：在要素市场上，一个城市可达性改善，扩大了该城市要素供给的市场范围，从而改善了要素供给条件。具体地，从劳动力要素供给来看，可达性条件的改善，使可供本地制造业企业使用的潜在劳动力供给范围由本地扩展至周边城市。而潜在劳动力市场范围的扩大，不仅有助于企业的用工缺口及时得到补充，同时也有利于在充分的劳动力市场竞争中获得适合企业发展的优质劳动力。从资本要素供给来看，可达性条件的改善，有助于促进城市之间的跨城互动交流，减少了城市之间因信息不对称造成的合作难题。例如，两个城市之间的可达性提高，能够有效降低合作企业之间的监督成本，促进跨城企业间的投资合作。从技术要素供给来看，可达性条件的改善促进了城市之间的交流合作。无论是跨城企业之间的合作交流，还是技术人员的跨城、跨企业流动均会带来一定的技术和知识溢出，技术要素供给有助于提高企业生产率。在产品市场上，可达性条件改善，扩大了该城市企业产品供给的市场范围，有助于企业产品的输出，从而提高企业经营绩效。要素供给条件的改善和产品市场范围的扩大，优化了城市的区位条件，吸引了制造业企业在该城市集聚。

2.间接效应

间接效应也即空间溢出效应。从表3可以看出，无论是用日常可达性系数还是可达性潜力变量作为城市高铁可达性的替代变量，间接效应的系数为正且均至少在5%水平上显著，说明可达性改善的空间溢出效应十分明显。也即高铁带来城市可达性改善不仅有利于促进本地制造业集聚，同时会通过空间溢出效应提高与其邻近的铁路沿线城市的制造业集聚水平。高铁带来的城市可达性改善之所以存在显著的空间溢出效应，主要原因在于交通基础设施具有较强的网络性，高铁提高了整个铁路网络的运行效率，极大压缩了城市之间的旅行时间，为生产要素的跨地区流动提供了便利，且能提高城市的经济辐射能力。城市间禀赋存在差异，形成了不同的比较优势。在可达性水平较低时，受交通成本的限制，生产要素的跨区流动较为困难，本地企业也不易将本地的生产能力向周边外溢。高铁带来可达性改善，减少了生产要素和生产能力跨区流动的成本约束，促进了本地区相对过剩的要素和生产能力向周边地区转移。因此，高铁不仅会促进本地制造业集聚，也会通过空间溢出效应促进沿线邻近城市的制造业集聚。

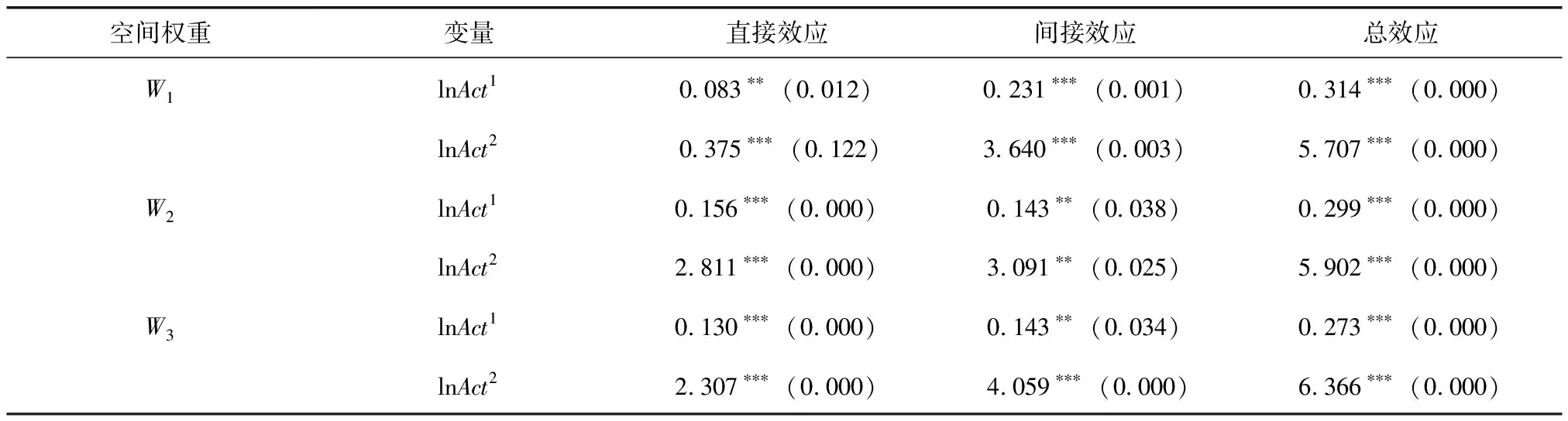
表3 直接效应、间接效应与总效应

(三)行业异质性分析

制造业各行业要素投入不同，生产的产品各异，这使得对制造业各行业进行分类考察显得十分必要。上文考察了高铁带来的城市可达性提高对制造业整体集聚的影响，这部分分别考察城市高铁可达性对制造业不同行业的异质性影响。本文借鉴鲁桐和党印(2014)[24]的做法，将制造业各行业按照要素投入密集度将制造业行业分为劳动密集型、资本密集型和技术密集型行业，进行分行业回归比较(5)劳动密集型制造业包括农副食品加工业(13)，食品制造业(14)，饮料制造业(15)，烟草加工业(16)，纺织业(17)，纺织服装、鞋、帽制造业(18)，皮革、毛皮、羽毛(绒)及其制品业(19)，木材加工及木、竹、藤、棕、草制品业(20)，家具制造业(21)等9个二位数制造业行业。资本密集型制造业包括造纸及纸制品业(22)，印刷和记录媒介复制业(23)，文教体育用品制造业(24)，石油加工、炼焦及核燃料加工业(25)，化学原料及化学制品制造业(26)，化学纤维制造业(28)，橡胶和塑料制品业(29)，非金属矿物制品业(30)，黑色金属冶炼及压延加工业(31)，有色金属冶炼及压延加工业(32)，金属制品业(33)等11个二位数行业。技术密集型制造业包括医药制造业(27)，通用设备制造业(34)，专用设备制造业(35)，交通运输设备制造业(36)，电气机械及器材制造业(37)，计算机、通信和其他电子设备制造业(38)，仪器仪表制造业(39)等7个二位数行业。。表4—表6分别报告基于地理距离权重、经济地理距离权重和制度地理距离权重的估计结果。可以看出，在地理距离权重下的资本密集型和技术密集型行业中，无论是可达性潜力还是日常可达性系数变量的直接效应均为正，且至少在5%水平上显著。说明高铁发展带来的本地城市可达性水平的提高能够有效促进制造业集聚；间接效应也均为正，且在1%水平上显著，说明高铁带来的城市可达性水平的提高也能够通过铁路的网络效应促进周边城市的制造业集聚水平的提高，存在显著的空间溢出效应。从总效应来看，在资本密集型和技术密集型行业中，高铁发展带来的城市可达性提高对外围城市制造业集聚影响的总效应均为正值，且均在1%水平上显著。对于劳动密集型行业而言，可达性潜力和日常可达性系数变量的总效应均为负，且通过了1%水平的显著性检验，说明可达性改善并没有促进劳动密集型制造业集聚，而是会对其产生抑制作用。之所以出现这种情况，主要原因在于：相比资本密集型行业和技术密集型行业，劳动密集型制造业行业生产需要依靠大量的低廉劳动力投入，但由于其生产产品本身的附加值较低，无法提供较具竞争力的工资，这就决定了高铁发展带来的可达性水平提高，实际上并不能对该行业的劳动力流动产生明显的影响，相反可能会由于可达性改善带来的要素价格上升而不利于本地区劳动密集型制造业集聚。

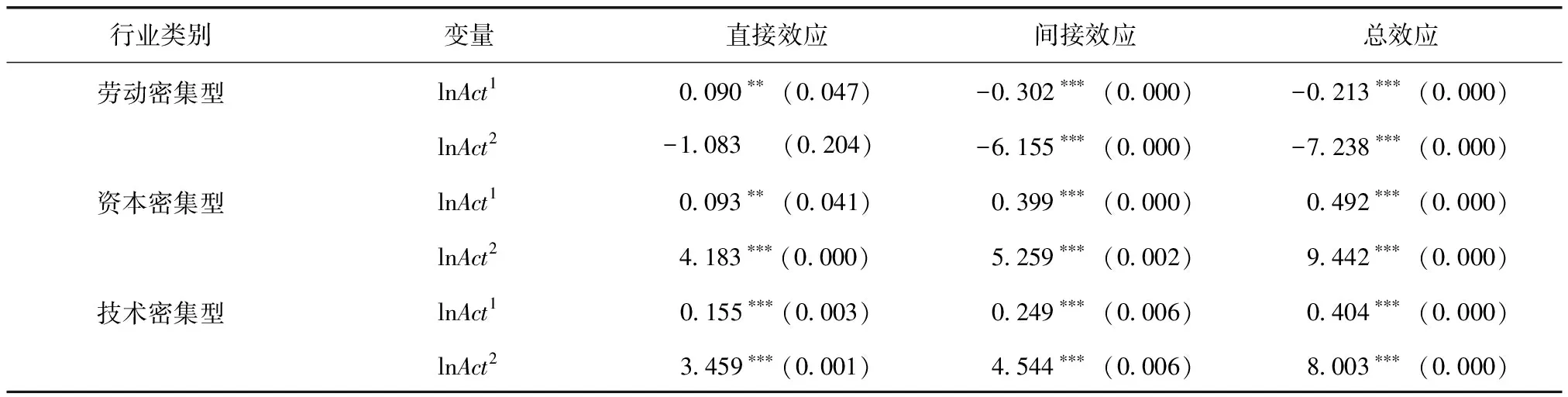
表4 地理距离权重下直接效应、间接效应与总效应估计结果

表5 经济地理距离权重下直接效应、间接效应与总效应估计结果

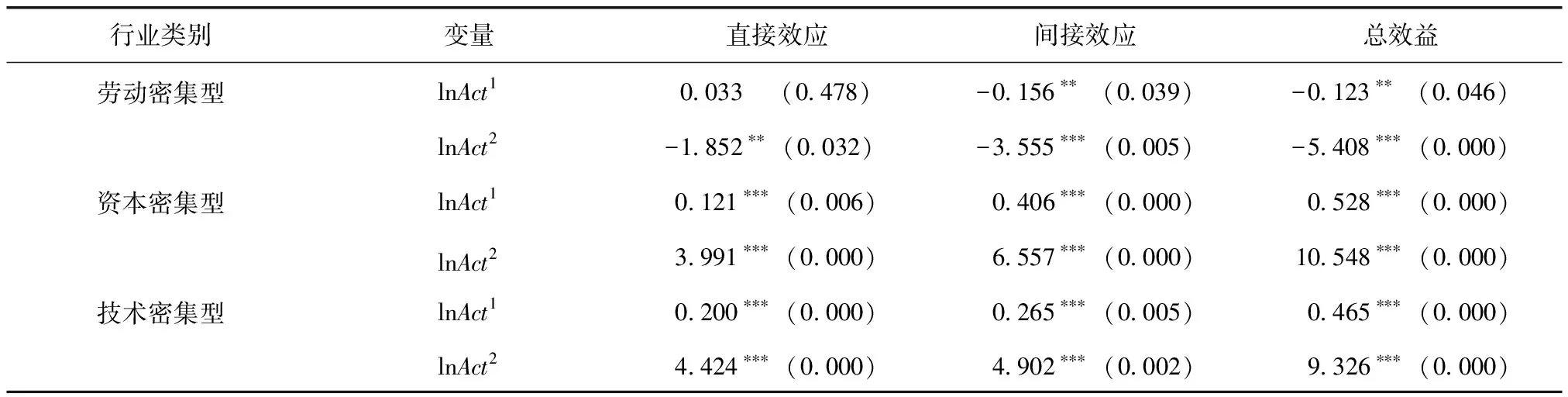
表6 制度地理距离权重下直接效应、间接效应与总效应估计结果

(四)稳健性检验

1.稳健性检验一：基于产值计算的区位熵指数

上文采用就业人数计算区位熵指数，分析高铁带来的城市可达性提高对制造业集聚的本地影响及空间溢出效应，那么如果采用制造业产值计算区位熵，实证结果是否依然成立呢？为了确保实证结果的稳健性，本文用制造业产值计算的区位熵指数替代就业人数计算的区位熵指数对式(16)进行回归，以检验实证结果的稳健性。

以产值代替就业人数计算制造业区位熵进行的回归结果显示，在不同权重下，直接效应均为正值，且在1%水平上显著。间接效应也为正值，也在1%的水平上显著。替换被解释变量的估计结果仍然支持高铁带来的可达性改善对本地制造业集聚有显著的正向影响及对邻近城市制造业集聚有正向空间溢出效应的实证结论(6)限于篇幅，未列示回归结果。。

2.稳健性检验二:更换数据来源的回归结果

本文用产值区位熵替代就业区位熵验证实证结果的稳健性，但制造业产值指标仍然来源于国家统计局公布的中国工业企业数据库微观加总数据，那么如果更换数据来源检验结果是否有很大差异呢？如果有很大差异，本文的实证结论可能并不可靠。基于此，本文采用《城市统计年鉴》中规模以上工业总产值数据，替代稳健性检验一中采用的工业企业数据库加总的制造业产值数据，计算产值区位熵指数，进行回归检验。替换了数据来源之后，实证结果仍然支持本文的结论。(7)限于篇幅，未列示回归结果。

五、基本结论与启示

本文以66个具有高铁客运站点的非区域中心城市为考察样本，基于可达性视角，运用空间杜宾模型考察高铁可达性及其空间溢出效应对区域非中心城市制造业集聚的影响。研究得出以下几点结论：一是从整体上看高铁可达性的改善对非区域中心城市制造业集聚水平提高产生显著的正向影响，同时会通过空间溢出效应，提高地理邻近、经济邻近及制度邻近城市的制造业集聚水平。二是分行业来看，高铁可达性改善对制造业的本地影响及空间溢出效应会因制造业行业不同而有所差异。具体来看，高铁可达性对制造业的本地影响及空间溢出效应在资本密集型和技术密集型行业均十分明显，高铁可达性的改善不仅有助于提高城市本地的资本密集型行业和技术密集型行业的集聚水平，同时会通过空间溢出效应提高与其邻近城市的制造业集聚水平。但对于劳动密集型行业而言，可达性改善的总效应显著为负，这意味着高铁可达性改善会对劳动密集型行业集聚产生显著的负向抑制效应。这种负向抑制效应不仅体现为对本地劳动密集型行业集聚的负向影响，同时也体现于与该城市邻近城市的劳动密集型行业的负向溢出效应。

基于研究结论，本文提出如下政策建议：一是在进行高铁规划时，应该充分考虑高铁的空间重塑效应，在减少重复建设的同时，推进高铁网络向非区域中心城市以及欠发达地区延伸，让更多的城市接入高铁，尽可能实现高铁服务供给的区域协调发展；二是未开通高铁的非中心城市应该正视高铁对本地制造业发展的重要意义，努力寻求与中心城市合作，开展城际高铁和其他城际交通基础设施的规划和建设，使自身更好地融入中心城市经济圈，同时充分发挥自身在要素价格方面的比较优势，加强营商环境建设，以更好地承接制造业的产业转移。