基于改进K-means的羊体点云分割方法

刘 娜，薛河儒，马学磊

（内蒙古农业大学计算机与信息工程学院，内蒙古呼和浩特 010011）

【研究意义】在畜牧养殖业中，传统的接触式羊体尺测量不仅测量精度低，耗时长，且易使羊产生应激反应等问题，因此无接触体尺精准测量成为目前畜牧养殖业中的研究热点。研究表明，羊体点云分割是利用机器视觉实现羊体尺无接触精确测量的重要环节。能够从具有复杂背景的点云中精准的分割出羊体点云，可有效地提高无接触式[1]羊体尺测量[2-4]精准度，从而对羊进行准确的体征分析，如体尺、体质量等。【前人研究进展】当前，国内外针对三维点云分割的方法主要有：边缘检测法、模型拟合法、区域增长法和特征聚类法。边缘检测法[5]-[6]是通过标识点云图像中特征变化明显的点，去除不相关的点云信息，实现除边缘外的点云数据的分割。主要有：基于体素栅格和八叉树的方法进而对点云图像进行边界识别，以完成点云分割；引入Alpha-Shapes条件判断对点云图像进行地面边缘检测。模型拟合法[7]：根据三维点云的空间几何特征选择合适的几何模型进行匹配。主要有：利用随机采样一致性算法检测三维点云中存在的平面、球体、长方体、圆柱体等几何模型，进而得到点云分割结果。区域增长法[8-10]：它是根据具体点云数据的特征，选择恰当的种子点并从此点开始增长，搜索指定邻域内满足自定义生长准则的点云集合。主要有：利用Octree 对城市点云数据进行区域增长，进而完成分割；通过引入点云曲率信息，从而确定种子点的选择，根据自定义的生长准则，得到较好的分割效果；结合超体素和区域生长法，对所选取的植物3个物候期的点云数据进行分割。特征聚类法：是将点云数据按照指定的数据特征，把特征相同或相似的点云划分到同一类，不同类间点云数据属性独立。林国祥等[11]利用传统K-means 聚类的方法对单档电力线激光雷达点云进行分割，但分割结果不稳定；Swita等[12]根据引入的密度信息确定初始聚类中心，进而完成对K-means 聚类算法的改进，提升了算法的执行速度；孙红岩等[13]利用谱系聚类和改进的K-means 聚类算法对三维点云数据进行分割，试验证明其改进的聚类算法分割效果更好。【本研究切入点】传统K-means 点云分割，随机选择K 个初始聚类中心，并将点云中的每一个点划分到距离最近的初始聚类中心所在的聚类区域中，最终得到类内点云数据属性相同，类间数据属性独立的K个点云集合。但传统K-means 聚类分割算法的不足在于：（1）在计算点云中每个点到聚类中心的距离时，只使用点云的三维坐标值进行计算，参与计算点距离的点云数据属性单一，导致算法对点云曲面特征变化的敏感性较差；（2）初始聚类中心随机选取导致分割结果不固定。【拟解决的关键问题】研究旨在针对以上问题，结合羊体点云数据的特征，引入点云的曲率信息，对传统K-means 算法进行改进。首先，计算点云数据的曲率，利用点云的曲率信息对点云间的距离进行约束。其次，选取点云主曲率最大的前K个点作为K-means 分割算法的初始聚类中心，以期实现对点间坐标距离很近但曲面变化较大的羊体点云进行精确分割及保证分割结果的唯一性和稳定性。

1 材料与方法

1.1 点云数据采集

采用易福门制造的型号为O3D303的三维摄像机进行数据采集，镜头孔径为60°× 45°，图像分辨率为352像素× 264像素。摄像机需外接电源为其供电，借助以太网和计算机对目标物体进行数据采集，可实时记录获取到的点云数据。与激光扫描仪相比，三维摄像机获取点云数据冗余量较小，且更方便快捷。研究试验对象为3周岁的苏尼特羊标本，使用一台三维摄像机对其进行数据采集。进行数据采集时，摄像机自动建立空间直角坐标系，并以摄像机所在的点为坐标原点，垂直于地面方向为x轴，垂直于羊体点云所在的平面方向为z轴，垂直于x、z轴所在的平面方向为y轴。如图1所示，共获取20 266个点云数据。

1.2 点云预处理

对原始点云进行适当的点云预处理，是点云分割的必要前提。通过摄像机获取的原始点云数据中存在一些离羊体点云较远的无效点，如图1中羊体的背景，以及左右两侧的书桌。因此，需要对原始点云进行滤波，滤除无效点。根据无效点云的特征，采用直通滤波将不在范围内的点云滤除。对原始羊体点云数据进行直通滤波时，在x，y，z轴上的滤波取值范围分别为0.0～0.0 m（在x轴上不需滤除无效点）、-0.59～0.65 m、1.1～2.0 m。使用直通滤波滤除羊体点云中的离散点，可提高后续算法的精度。经直通滤波后，点云数据中依然存在噪声点及无效点。采用统计滤波[14-15]对其进行准确滤除。统计滤波是通过统计点云数据中某一点与其在设定邻域内的点集之间的距离，以滤除不符合条件的无效点。在该算法中有两个参数需要设置，邻域点数目k和标准差倍数阈值。试验中，设定k为25，标准差倍数阈值为1。原始羊体点云经点云滤波后的实验结果如图2所示。经直通滤波和统计滤波处理后，羊体点云数据量分别为9 395个、8 483个。

图1 复杂背景下原始羊体图像Fig.1 Original sheep body image under complex background

图2 羊体点云数据的滤波结果Fig.2 Filtered results of sheep point cloud data

滤波后的点云数据在去除了噪声的同时，数据量也有所减少，但其密度依然很大，因此，计算效率较低[16]。试验在能确保点云特征不变的情况下，使用体素栅格的方法对冗余数据进行适当的下采样[17]可大幅度降低点云分割计算量，提高效率。首先，对经统计滤波后的点云数据采用八叉树算法进行体素化；其次，确定每个小立方体素栅格的重心，使用距其空间位置最近的点云数据代表每个体素栅格。在确保点云数据经下采样后形状特征不发生改变的情况下，对滤波后的点云数据进行疏密判断，设置小立方体素边长为0.025 cm[18]。体素化前后点云数据量分别为：8 483个、3 441个，如图3所示。

图3 体素化后的羊体点云Fig.3 Sheep body point cloud after voxelization

1.3 改进k-means点云分割

试验为实现数据预处理后点云数据的精准分割，针对传统K-means 分割算法存在的不足，提出了利用曲率约束点距离和选取曲率最大的前K个点作为初始聚类中心的计算方法。

1.3.1 曲率约束点距离的计算 由于采用传统欧式距离对三维点云数据的点距离进行度量时，分割效果不准确。试验根据羊体点云数据特点，考虑引入点云数据的曲率信息，对三维点云数据的点距离进行重新定义，以实现羊体点云数据的细分割。具体定义如下：

定义1.点向量表示。假设点云集F第i个数据点fi的坐标为，数据点fi的高斯曲率为，平均曲率为，由高斯曲率和平均曲率构成曲率向量主曲率为，则点fi的向量表示为公式①：

（1）点云曲率计算。曲率是反应物体空间几何特征的决定性因素［19］，因此羊体点云表面的弯曲程度可由曲率进行描述。采用kd-tree 建立点云数据之间的拓扑关系，利用二次曲面拟合[20]方式计算点云数据的曲率。

对于给定的三维点云集｜F={fi|fi∈R3,i=1,2,…,n}中的任意点fi及fi的k近邻点集Neighbor(f)i，进行二次曲面拟合，其方程为公式②：

曲面的弧长可决定曲面的第一基本形式，可表示为公式③：

若(u0,v0)与近邻点的距离表示为公式④：

则曲面第二基本形式可表示为：

由此推导出计算主曲率的公式：

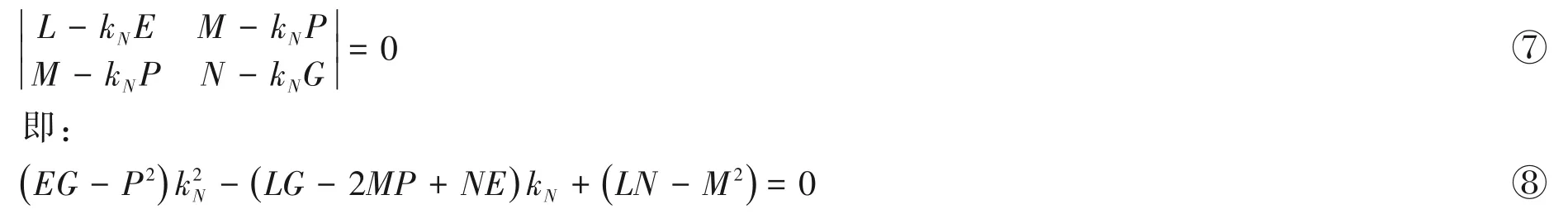
其中，kN表示主曲率，取值为k1和k2。由此可得：

高斯曲率K为：

平均曲率H为：

整理公式（8）、（9），可得主曲率的取值：

（2）点云间距离计算。传统K-means分割算法中，使用欧式距离衡量点云中每一点到聚类中心的距离。欧氏距离仅使用点云的三维坐标参与计算，其数据属性单一，对羊体点云表面的曲面特征变化没有给出有效的衡量方式。因此对于给定的距离阈值，即使羊体表面点云数据曲率变化显著，但当前点云到最近的聚类中心距离值在给定阈值范围之内，此点云依然会被划分到此聚类中心所在的聚类区域中。为了能得到精确的点云分割效果，试验引入曲率信息对点距离进行计算。

定义2.点云间的距离。假设给定点云集F中任意两点：fi=（xi，yi，zi，Ki，Hi，ki1，ki2），fj=（xj，yj，zj，Kj，Hj，kj1，kj2），则两点之间的空间距离可定义为：

其中，DB(fi,fj)表示点fi与fj之间的欧式距离，DQ(fi,fj)表示点fi与fj之间距离的曲率约束，α表示调整参数。则DB(fi,fj)的计算公式为：

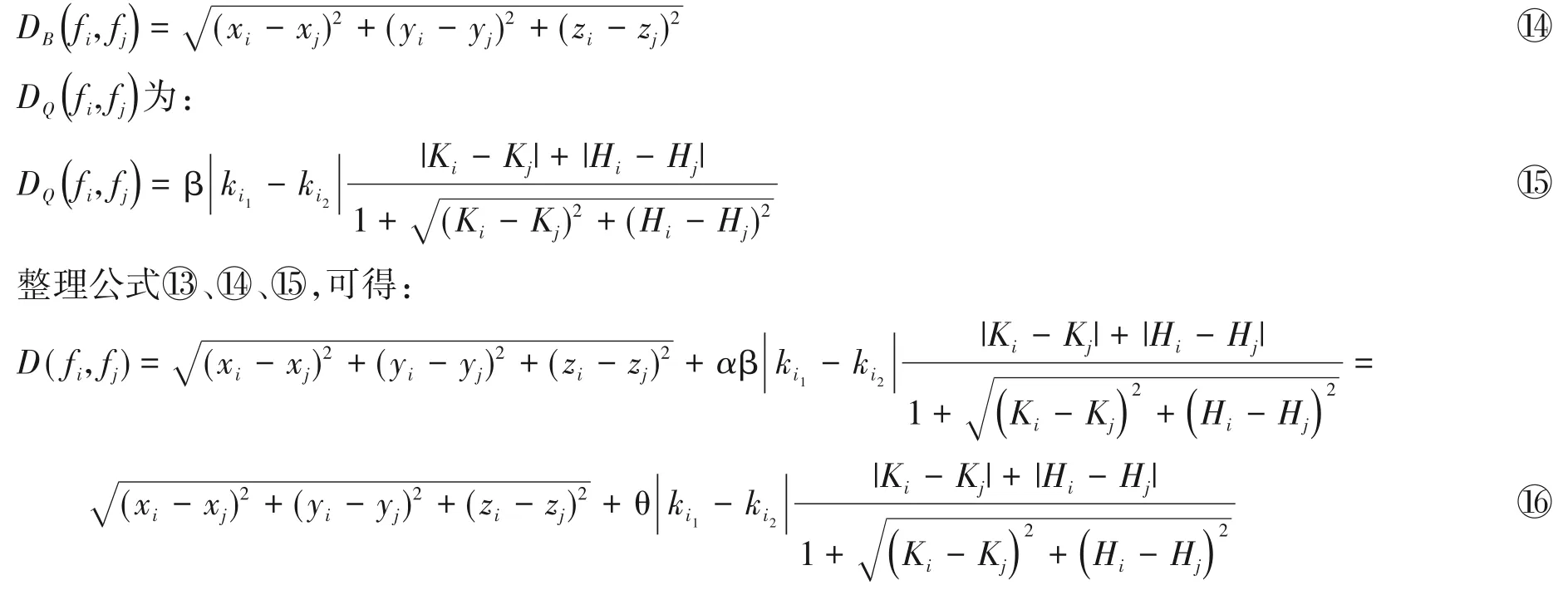
其中，θ=αβ，θ为曲率调整参数。当点云曲面特征变化明显，需要把当前点云分割出当前聚类中心所在的区域时，调整θ的取值，使其适当增大。

1.3.2 聚类中心的选取 在基于聚类的分割算法中，初始聚类中心选择的优劣直接影响分割效果。因此，根据不同点云图像的特征，选择适当的初始聚类中心是获得准确分割效果的重要前提。针对传统K-means 分割算法随机选择初始聚类中心导致的分割结果不稳定，且分割效果不准确的缺陷，经多次试验研究，利用主曲率k2作为选择羊体初始聚类中心的依据，并且选择曲率最大的前K 个点作为初始聚类中心，可提高分割效果的准确性和稳定性。

1.3.3 聚类算法的实现 对于点云集合F={fi|fi∈R3,i=1,2,…,n}，分割成K个聚类区域，则可定义准则函数为：

其中，点云集合F的第i个聚类区域表示为Si，Si中任意一点表示为f，Si的聚类中心表示为ci。

点云集合中任意点f被划分到具体聚类区域中的判定公式：

对于不满足收敛条件的聚类区域，更新其聚类中心的公式为：

其中，n表示聚类区域中包含的点数量。

基于改进K-means的羊体点云分割算法步骤如下：

（1）对采集到的点云图像进行数据预处理。（2）计算经预处理后点云数据的高斯曲率K、平均曲率H及主曲率k1、k2，由此得到点云向量（3）利用主曲率k2作为选取初始聚类中心点的依据，选取曲率最大的前K 个点作为初始聚类中心。（4）通过公式○16得到点云集合F中每一点到{c1,c2,…,ck}中各初始聚类中心的距离。（5）根据公式○18，将（4）中所得距离聚类中心最近的点聚类到该聚类中心所在的区域{S1,S2,…,Sk}。（6）按照公式○19 更新{S1,S2,…,Sk}中各聚类区域的聚类中心，得{c1,c2,…,ck}，重复（4），（5）。（7）直到更新的聚类中心点集{c1,c2,…,ck}不再发生变化或者收敛于E，结束聚类，得到最终分割结果。

2 结果与分析

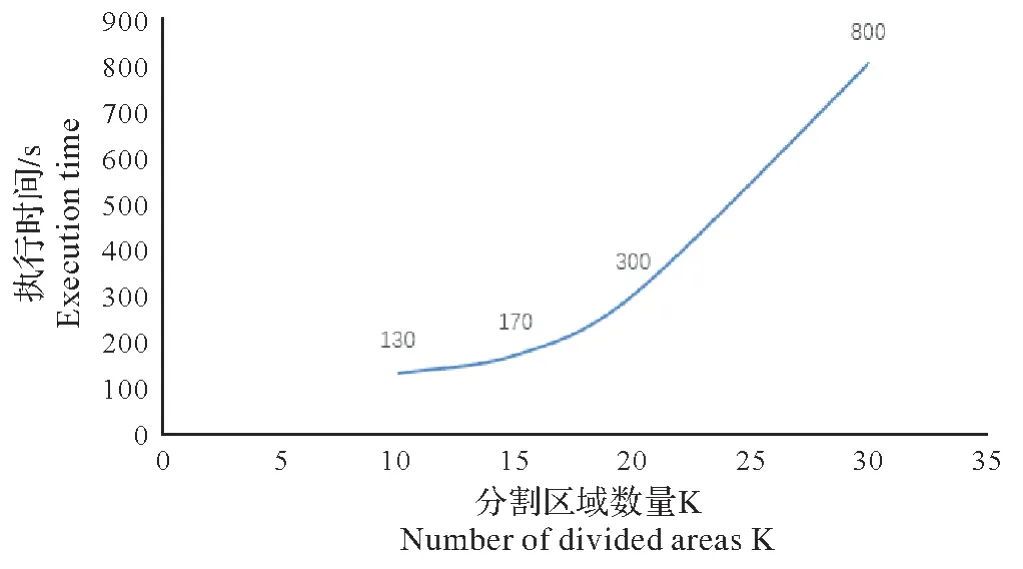
图4 K增长时算法执行时间Fig.4 Algorithm execution time as K grows

研究使用CPU 为Inter（R）Core（TM）i7-8550U CPU@1.80 Hz 2.00 GHz，16 G 内存的计算机进行试验，应用Visual C++2017 编程环境，基于PCL开源C++编程库，分别用传统K-means分割算法和改进K-means分割算法对羊体点云数据进行分割。图4 为采用改进的K-means 分割方法对羊体点云数据进行分割的过程中，初始聚类中心K 与算法执行时间T 的关系。由图可知，当K取10～20 时，算法执行时间增幅较缓；随着K 不断增大，当K取20 以上时，算法执行时间增幅较大，时间开销大，K 值不可用。实验过程中发现，当K取10～15时，初始聚类中心数量过少，分割效果不佳，K值不可用。

图5 K和θ一定时，曲率排序选取初始聚类中心和随机选取初始聚类中心的分割对比结果Fig.5 The results of segmentation comparison between initial clustering center and random clustering center selected when theKandθare fixed

图5（a）-图5（f）为采用改进K-means分割算法进行分割试验过程中，当K和θ一定时，对点云数据进行曲率排序选取初始聚类中心和随机选取初始聚类中心的分割对比结果。

其中，图5（a）、（c）、（e）分别为K取16、18、20时，利用曲率排序选取初始聚类中心进行分割，所得的最佳聚类结果，但仅图5（c）（K=18,θ=0.9）分割效果较为理想。由图5（a）-图5（f）对比可知，利用曲率排序选取初始聚类中心相较于随机选取初始聚类中心得到的分割效果更好。

图6 为利用传统K-means 算法进行分割的结果。传统K-means 算法在曲面曲率变化显著的区域仍按照欧式距离进行聚类，因此羊体脚部与地面接触的区域无法精确分割。图7（a）-图7（h）为利用改进的K-means聚类算法在K一定(K=18)的前提下，θ取不同值时的聚类结果。当θ=0.1 时（图5（a）），曲率对点距离约束较弱，导致不同聚类区域的点被分割到同一区域中，出现欠分割现象（图5（b））；当θ取值逐渐增大时（图5（c）），曲率对点距离的约束逐渐增强，分割效果准确性逐渐提高；当θ取值过大时（图5（g），θ=5），曲率对点距离约束过强，导致同一聚类区域的点被划分出去，出现过分割现象（图5（h））。相对来说，θ=0.9 时的分割效果较为理想，图5（f）为从图5（e）中提取出的羊体点云数据，分割结果达到了预期。图7（a）-图7（b）为利用改进的K-means分割算法，在K=18，θ=0.9 时，以羊体点云数据中随机选取的点作为初始聚类中心进行分割的结果图。可以看出，两次试验的分割结果明显不一致且均不准确。与图5（f）相比，后者分割结果更具稳定性和准确性。研究改进的K-means 算法可将羊体从地面准确的分割出来，且避免了传统K-means 算法随机选取初始聚类中心导致的分割结果不稳定及不精确的问题。总体分割效果较好，可提高后续测点识别度。

图6 传统K-means分割结果Fig.6 Traditional K-means segmentation results

图7 改进K-means分割结果Fig.7 Improved K-means segmentation results

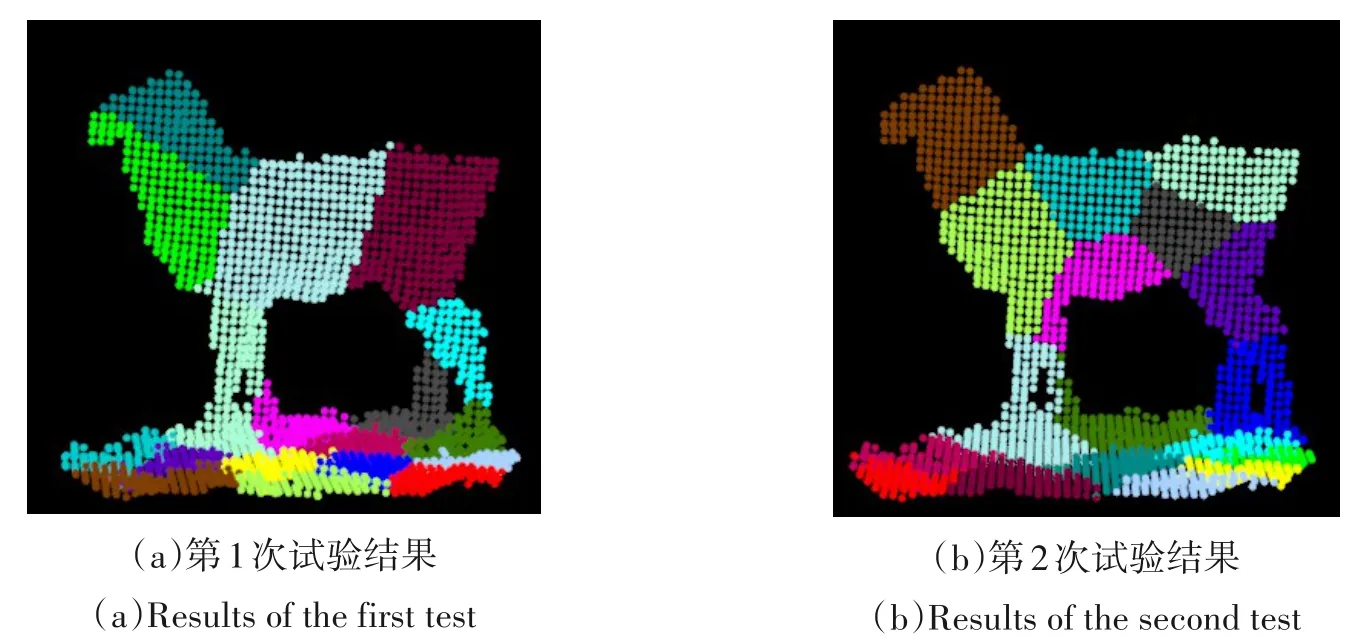
图8 随机选取初始聚类中心不同试验的分割结果Fig.8 Segmentation results of randomly selected initial cluster centers with different trial times

3 结论与讨论

研究采用改进的K-means 羊体点云分割方法，引入曲率信息，对点云间的距离进行重新定义，实现了羊体点云数据曲率变化显著部位的准确分割。同时，对点云的主曲率k2排序，选取曲率最大的前k 个点云作为初始聚类中心，避免了随机选择初始聚类中心存在的弊端，提高了分割效率。以此分割结果作为下一步羊体测量点识别的试验依据，对羊体的无接触测量具有重要的研究意义。

采用改进的K-means算法对所采集到的羊体点云数据进行分割的过程中，可以通过手动调节θ的取值，来获得较为理想的分割效果。为进一步提高羊体分割的准确性，可以采用去羊场拍摄活体羊同时增加羊体点云数据样本数量的方式，以提高分割模型在恶劣环境下的分割能力。

致谢：内蒙古农业大学计算机学院薛河儒教授对研究给予了指导与支持，马学磊博士对研究给予了帮助，谨致谢意!