概率q阶犹豫模糊熵及其应用

尹文静，郑婷婷，李龙妹

(安徽大学 数学科学学院 安徽 合肥 230601)

0 引言

自1965年Zadeh[1]提出模糊集理论以来，该理论为解决一些不确定性问题提供了重要手段。 随着模糊集理论的深入研究，它被扩展到许多领域，如直觉模糊集[2]、二型模糊集[3]等,并且学者们将这些理论成功应用于属性约简、多属性决策问题[4-5]。 2017年，Yager[6]提出了q阶模糊集的概念，主要是考虑到直觉模糊集与毕达哥拉斯模糊集对于隶属度与非隶属度的取值范围有限，而这个概念的提出能更好地解决直觉模糊集和毕达哥拉斯模糊集不能表示的模糊问题。 Liu等[7]和Peng等[8]研究了q阶模糊集环境下的不确定性度量，并解决了一些模式识别、医学诊断和聚类分析等问题。在许多实际情况下很难定义隶属度函数，因此Torra[9]提出了犹豫模糊集理论，为处理多个隶属度的情形提供了有效的途径。 朱斌[10]为犹豫模糊集增加了概率，可以有效地反映决策者的偏好在决策中的作用，并将新的犹豫模糊集命名为概率犹豫模糊集。

为了度量不确定信息，Zadeh[11]于1968年提出了模糊熵的概念来度量模糊集的模糊性。 模糊熵的概念很快被扩展到直觉模糊集[12]，并成功地应用于模式识别、属性决策[13]等问题。此外，随着犹豫模糊集的发展，犹豫模糊熵成为一个重要的研究方向。2012年，Xu等[14]给出了犹豫模糊集模糊熵与交叉熵的概念,并根据定义提供了一系列具体的公式。但是，随着研究的不断深入，现有的犹豫模糊熵中仍然存在不足,需要探究新的犹豫模糊熵以更加有效地反映信息的不确定程度。本文在充分结合q阶模糊集和概率犹豫模糊集优点的基础上，提出了概率q阶犹豫模糊集的概念，并给出了概率q阶犹豫模糊熵的公理化准则；利用几何方法构造了概率q阶犹豫模糊集的熵平面，讨论了参数α对熵的影响，将其推广到广义概率q阶犹豫模糊熵，并应用概率q阶犹豫模糊熵解决了多属性决策问题。

1 预备知识

1.1 概率犹豫模糊集

定义1[10]设U为一个有限论域，论域U上的概率犹豫模糊集H定义为

H={〈x,hH(x)(pH(x))〉|x∈U}，

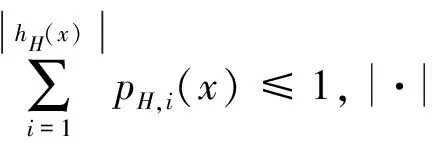
1.2 q阶犹豫模糊集

2 概率q阶犹豫模糊集

3 一种新的概率q阶犹豫模糊熵

结合文献[13]中直觉模糊熵的公理化准则，提出了概率q阶犹豫模糊熵的公理化准则。

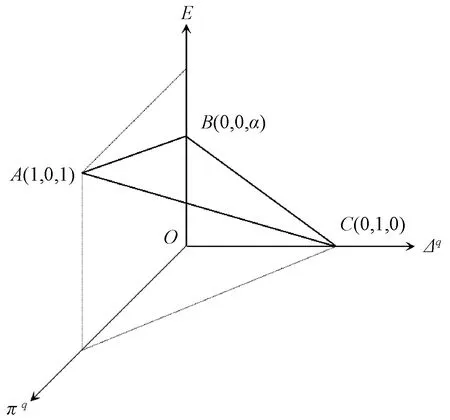
图1 概率q阶犹豫模糊熵平面(πq,Δq,E)Figure 1 Probabilistic q-rung orthopair hesitant fuzzy entropy plane (πq,Δq,E)

式中：0<α<1。

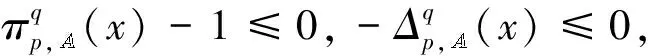
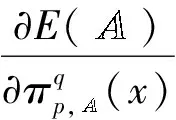
式中：Mπ,E表示犹豫度对熵的影响；MΔ,E表示核值对熵的影响。 显然，当Mπ,E=MΔ,E时，核值与犹豫度对熵的影响速率相同。 为了便于讨论，给出替代率的概念，即

RSπ,Δ=α/(1-α),RSΔ,π=(1-α)/α，

式中：RSπ,Δ表示核值相对于犹豫度的替代率；RSΔ,π表示犹豫度相对于核值的替代率。当α<0.5时，犹豫度相对于核值的替代率更强一些；当α>0.5时，核值相对于犹豫度的替代率更强一些；当α=0.5时，犹豫度与核值的相互作用相同。

4 广义概率q阶犹豫模糊熵

本小节将概率q阶犹豫模糊熵推广到一般情况，并分析该公式的特征。

定理2定义8的模糊熵公式满足定义6的四条公理化准则。

证明定理2的证明过程与定理1类似，这里省略。

接下来讨论参数λ对概率q阶犹豫模糊熵的影响。

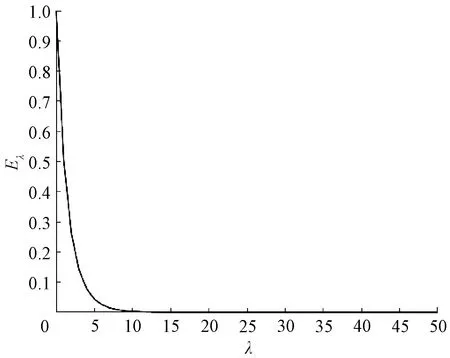
图2 λ对广义熵的影响Figure 2 The effect of λ on generalized entropy

证明设U={x}，计算可得

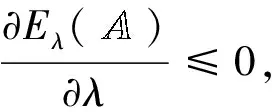
由此可见，不同的熵值可以代表不同的熵曲面，它们均可以反映不同概率q阶犹豫模糊集的模糊程度，同时也都满足熵的公理化准则。为了讨论上述熵测度在概率q阶犹豫模糊集中的合理性，将上述熵测度分别退化为q阶犹豫模糊集下的熵测度。

故此时可以得出退化后的熵测度为

通过分析可以发现，退化后的熵测度与文献[13]的基本准则一致，即满足熵随着犹豫度的增加而增大，随着核值的减少而增大。

5 多属性决策问题

5.1 决策步骤

步骤1确定属性权重。为了加强最优决策和确定信息的完整性，用熵测度来确定权重，

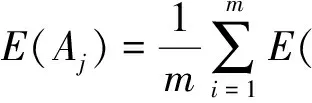
步骤2构建得分函数。得分函数可以表示为

步骤3对备选方案进行排名。对所有备选方案U={x1，…，xm}进行排序，根据得分函数S(xi)选择最佳方案。

5.2 实例分析

为了验证所描述方法的可靠性，以投资五家公司{x1,x2,x3,x4,x5}为例，它们满足四个属性{A1，A2，A3，A4}下的要求。为了选择最好的投资公司，对这些投资公司进行了评估，概率q阶犹豫模糊决策矩阵D如表1所示。取α=0.5，使用熵测度来确定权重，表2显示了λ=1、λ=2和λ=4三种不同情况下的属性权重。这三种情况下的得分函数S(xi)如表3所示，可知x2是最优的选择。

通过上述计算过程以及结果可以发现，q阶犹豫模糊集中每一个q阶模糊集发生概率的可能值是相等的，这显然不符合在实际决策中决策者在犹豫模糊环境下的判断和评估。因此，相比q阶犹豫模糊集，概率q阶犹豫模糊集可以保留更多的决策信息。

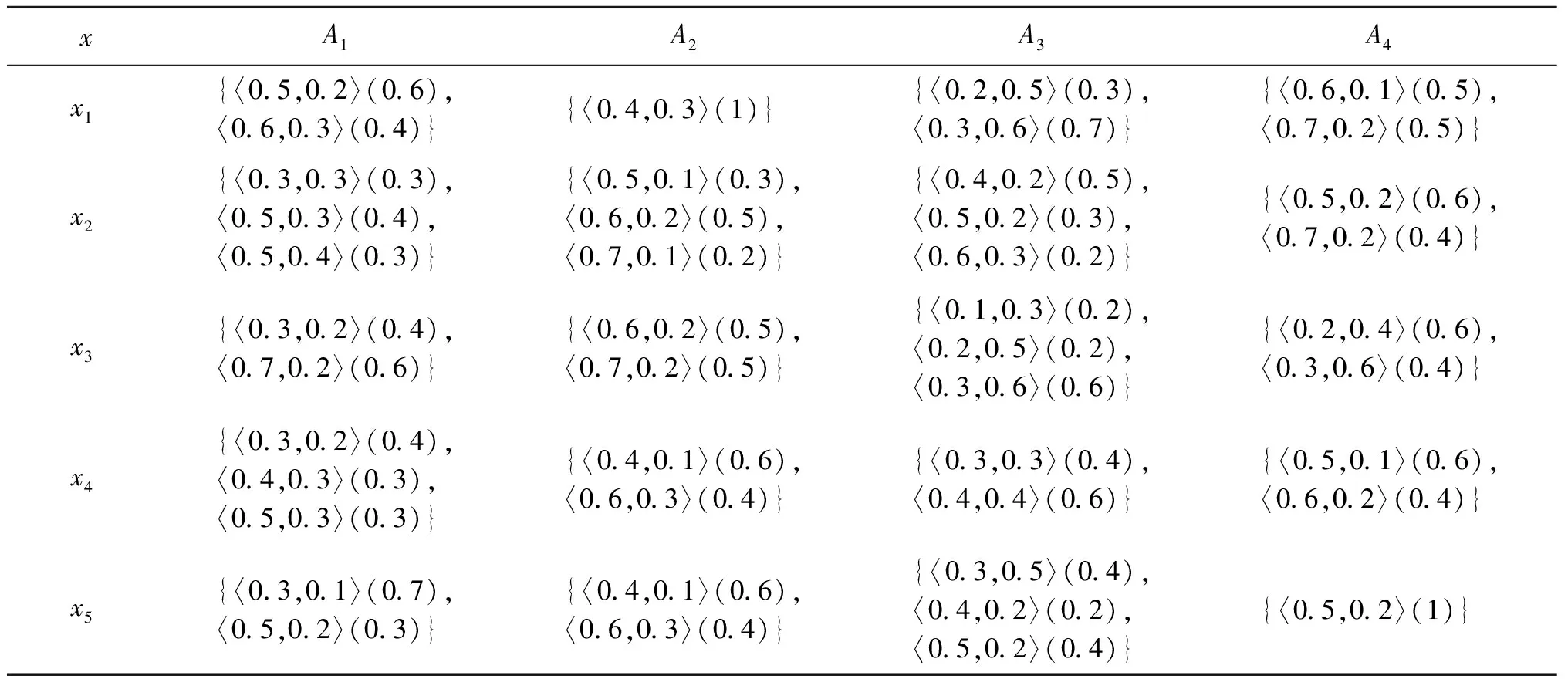
表1 概率q阶犹豫模糊决策矩阵DTable 1 Probabilistic q-rung orthopair hesitant fuzzy decision matrix D

表2 属性权重Table 2 Attribute weight

表3 得分函数Table 3 Score function

6 小结

本文结合了q阶模糊集与概率犹豫模糊集的优点，提出了概率q阶犹豫模糊集的概念，并且给出了概率q阶犹豫模糊熵的公理化准则。利用概率q阶犹豫模糊熵的几何特点构造了熵平面，并且提出了广义概率q阶犹豫模糊熵。概率q阶犹豫模糊熵的提出也为概率q阶犹豫模糊集的多属性决策问题提供了新的途径。