分析物理情境破解“叠加场滚轮线”模型

2020-11-18安徽徐建强

教学考试(高考物理) 2020年5期

安徽徐建强

(作者单位：安徽省蚌埠市北京师范大学蚌埠附属学校)

当带电粒子由静止释放以垂直磁场方向进入正交匀强电磁场(或正交重力场和匀强磁场)这类叠加场时，洛伦兹力与电场力或(重力不平衡)，则粒子做曲线运动，其运动轨迹为“滚轮线”。由于洛伦兹力的特性，利用动力学规律定量分析各时刻的运动规律比较复杂，处理起来难度较大。下面将从几个方面剖析该模型并用仿真软件绘制其轨迹，发现其规律特点，快速解题。

一、物理情景

(一)数学知识储备

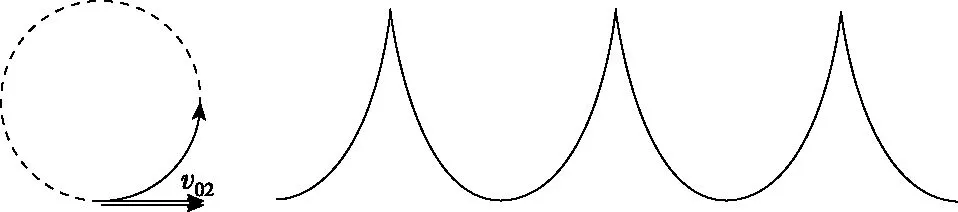
“滚轮线”是数学众多摆线中的一种，是匀速直线运动图像和匀速圆周运动图像的叠加图像。它的图像类似于正弦函数图像。可以类比为轮子上某质点“滚”出来的曲线。

(二)物理建模

受力分析：匀速直线运动要求合力为零，匀速圆周运动要求合力大小恒定，方向始终指向圆心。不难发现当带电粒子垂直磁场方向在正交匀强磁场和匀强电场(或重力场)中运动时，若所受电场力和洛伦兹力等大反向(速度选择器原理，不计重力)则可以做匀速直线运动。当带电粒子垂直进入匀强磁场时(不计重力)，将做匀速圆周运动。将这两种情景合成，就可以实现带电粒子在叠加场中做滚轮线运动。

运动分析：以运动的合成与分解的思想考虑不难发现，当某一质点在同一平面内的运动同时参与匀速直线运动和匀速圆周运动时，该质点的运动轨迹就是“滚轮线”。

二、处理方法

(一)配速法定量运算

图1

(二)功能关系法定量运算

(三)动力学法定性分析

从图1仿真轨迹可知，粒子在水平方向一直向右运动，竖直方向先向下后向上运动，所以从水平方向和竖直方向对粒子在AB间的运动进行动力学分析。从A到B过程，速度一直增加，洛伦兹力一直增大。水平方向合力Fx由洛伦兹力分力提供，方向一直向右、大小从零先增后减为零，则水平分速度vx一直增加；竖直方向分速度vy从零先增后减为零，反知竖直方向合力Fy先向下减小后向上增加(电场力不变，洛伦兹力竖直分量一直增大的结果)；B到C与A到B的情境对称。

仿真软件显示结果如图2，验证分析结果正确，同时发现：①关于最低点对称的两点水平方向速度相同，竖直速度大小相等方向相反；②关于最低点对称的两点水平方向加速度大小相等方向相反，竖直方向加速度相同；③粒子运动轨迹关于等高点对称，不能原路返回。理解掌握这些结论有利于快速解题。

图2

三、典例汇总

(一)静止释放

1.定性分析

【例1】如图3所示，水平放置的两个平行金属板MN、PQ间存在匀强电场E和匀强磁场B。MN板带正电，PQ板带负电，磁场方向垂直纸面向里。一带电微粒只在电场力和洛伦兹力作用下，从I点由静止开始沿曲线IJK运动，到达K点时速度为零，J是曲线上离MN板最远的点。以下几种说法中正确的是

图3

( )

A.在I点和K点的加速度大小相等，方向相反

B.在J点微粒受到的电场力等于洛伦兹力

D.微粒到达K点后将沿原路径返回I点

【点拨】此题为图1所示的滚轮线模型。①抓住粒子在I、K两点的速度都为零，可知受力情况相同，从而判定不会返回，这时关键点之一；②全程只有电场力做功，判定最低点速度最大，结合牛顿第二定律，可知qE>qvB。③在处理这类以动力学分析为主的试题中，抓住几个关键点的受力和运动情况再结合本文中的仿真结论，即可轻松解答。

2.定量分析

【例2】如图4所示，空间存在足够大匀强磁场，磁感应强度为B、方向垂直纸面向里。竖直平面中a、b两点在同一水平线上，两点相距l。一个质量为m、带电量为+q的质点P，从a点开始运动，重力加速度为g(空气阻力忽略不计)。

图4

(1)若以初速度v从a对准b射出，无论l取什么值，均可使P经直线运动通过b点，初速度v多大？

(2)若初速度v=0，可以将实际运动看成初速度为v1和v2=-v1的合成，则l取哪些值，可使P必定会经曲线运动通过b点？运动中离开直线ab的最大距离多大？运动中速度的最大值为多少？

【解析】(1)初速度v水平对准b点，为使P经直线运动通过b点，要求P所受洛伦兹力与重力平衡，则

qvB=mg

图5

运动中离开直线ab的最大距离为y=2R

瘦客户机（thin client）与传统PC机的功能相似，不同的是瘦客户机其实就类似于一个无盘工作站，数据和应用都存储在后台服务器上。瘦客户机自身只包含嵌入式高运算处理器、本地闪存、网卡、显卡和一些常用的外设等硬件。正是由于瘦客户机硬件配置简单优质的特性和后台服务器高速运算处理能力，才使得瘦客户机能够快速替代传统PC机得以推广应用。目前，瘦客户机作为服务器客户终端被应用在教育、政务、医疗等多个领域中，多媒体教学和计算机实训教室的应用是高校云终端最主流的应用场景。

根据运动的合成与分解可知，当v1、v2方向相同时，粒子运动到最低点，此时速度最大，则

【点拨】(1)该题第二问信息提示了配速法解答，运用合成与分解的思想结合匀速直线运动和匀速圆周运动的规律分析得出当两个分速度方向相同时实际最大速度，此时粒子运动到轨迹最低点(圆周运动最低点)，从而找到定量求解最大速度和对大竖直距离的突破口。(2)此题时重力和洛伦兹力共同作用下的运动也可以类比速度选择器模型，有助于打破各种模型之间的瓶颈，提升对物理问题本质的理解。

(二)以一定速度进入叠加场

1.定性分析

【例3】一个带正电的小球沿光滑绝缘的桌面向右运动，速度方向垂直于一个水平向里的匀强磁场，如图6所示，小球飞离桌面后落到地板上，设飞行时间为t1，水平射程为x1，着地速度为v1。撤去磁场，其余的条件不变小球飞行时间为t2，水平射程为x2，着地速度为v2，则下列论述正确的是

图6

( )

A.x1>x2B.t1>t2

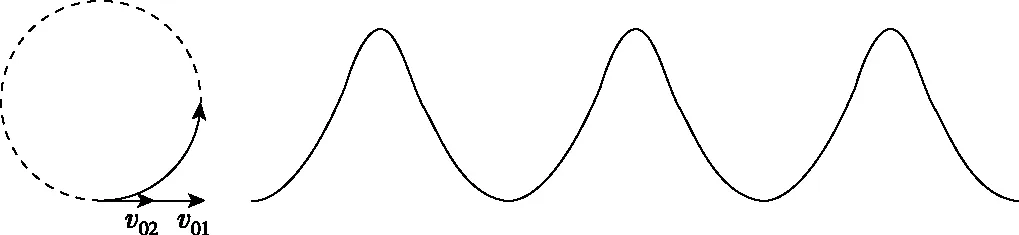
【解析】为深入理解有初速度条件下物体在叠加场中的运动情景，先抛开题设条件，下面通过配速法进行分析。

将小球的速度分解为向右的速度v01和另一个速度v02，其中v01满足qv01B=mg。由于v0大小的未知，因此可能存在下面几种可能：

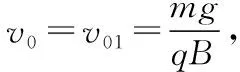
(2)若v0>v01，则v02向右，v01引起向右的匀速直线运动，v02引起逆时针的匀速圆周运动，这又有三种情况：①若v01

图7

②若v01=v02，则小球运动到最高点时合速度为零，轨迹如图8所示。

图8

③若v01>v02，则小球运动到最高点时合速度向右，轨迹如图9所示。

图9

(3)若v0

图10

由以上分析可知，题目所述情景是第(3)种情况，且只考虑方框内部分轨迹。结合动力学规律，可知小球在飞行过程中除重力外还受到斜向右上方的洛伦兹力作用，此力在水平方向上有向右的分量，竖直方向有向上的分量。由牛顿第二定律可知小球竖直方向上的加速度at2，选项A正确；小球水平方向上存在加速度，故x1>x2，选项B正确；又因为洛伦兹力不做功，落点速度大小相等，选项C正确；结合图10可知小球着地时速度方向不同，选项D错误。

【点拨】①以上全面剖析各种情况下，为更好理解配速度的应用，起到举一反三作用；②该题在解答时，掌握洛伦兹力不做功，只改变速度方向，即可判定小球在两次运动过程中，洛伦兹力起到上提小球的作用，所以飞行时间变长，运动水平位移变大，重力做功相同所以落地速度大小相同，实际可以秒杀。

2.定量分析

【例4】如图11所示，空间存在一范围足够大的垂直于xOy平面向外的匀强磁场和沿y轴正向的匀强电场，磁感应强度大小为B，电场强度大小为E。让质量为m，电量为q(q>0)的粒子从O点以初速度v0沿y轴正向发射。不计重力和粒子间的影响，求该粒子运动过程中的最大速度值vm(研究表明：粒子在xOy平面内做周期性运动，且在任一时刻，粒子速度的x分量vx与其所在位置的y坐标成正比，比例系数与场强大小E无关。)。