“另类”求解三力的静、动态平衡问题
2020-11-18福建黄红武
福建 黄红武 郭 威
(作者单位:福建省南平市浦城第二中学福建省南平市第九中学)
力的平衡作为高中重要的知识模块,对整个高中学习的重要性不言而喻,对三力静、动态平衡的求解方法也作为论文素材频见于期刊、学报,但求解方法大同小异,无外乎矢量图解法、相似三角形法、辅助圆法、正交分解法等一些针对基本题型的通法通解,但遇到一些力的静、动态平衡迁移问题时,用这些方法解决过程很繁琐或无法解决,在教学实践过程中总结出下面几种“另类”求解力的静、动态平衡问题的方法,细细品味却也蕴含着精妙的物理思维与方法,出奇制胜。
一、杠杆平衡原理法
这里的杠杆平衡原理法其实就是力矩平衡法,只是力矩知识大部分地区不作为高考要求范围,给学生讲力矩有超纲之嫌,但杠杆平衡原理学生在初中已经用得得心应手,所以我们可以借用杠杆平衡的思想来解决力的平衡问题,在教学实践中发现在研究对象不能看作质点的物体或系统时,用杠杆平衡原理法明显快捷得多。
【应用示例1】如图1所示,重为G的球静止于图示位置,绳与竖直方向的夹角为θ,与球相切于D,球与竖直墙面的接触点B,求绳的拉力FT,球与墙面的摩擦力Ff和弹力FN。

图1


图2
【方法点拨】此法关键在于灵活地选取支点,同一题可以通过选择不同的支点,尽量让不需要求解的力通过支点,使之力矩为零,这里的力矩=力×力臂,表示使物体转动的趋势,从而达到减小杠杆平衡式中力的个数。
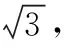

图3
( )
A.45° B.30° C.22.5° D.15°

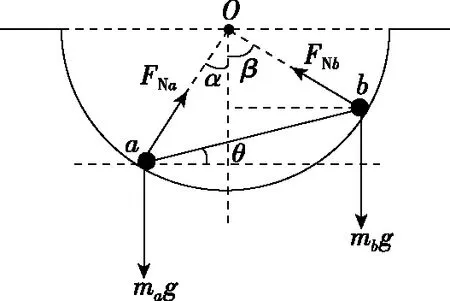
图4
二、微动态观察法
一个力大小不变,另两个力的方向都在变化的问题,用常规方法是采用相似三角形求解,但此类问题有时相似三角形并不适用,教学实践中发现很多人在求解此类问题时不知所措,用正交分解等方法又因为数学过程过于繁杂费时费力,所以基于该动态分析基本为定性分析,在两个方向均发生变化时,采用微动态矢量图法,观察每经过微小过程中矢量三角形中各力的大小变化从而得出结论,事半功倍。
【应用示例2】如图5所示,光滑小球用一根不可伸长的细绳系住,绳的另一端经过半圆形的光滑碗的边缘A点。现用水平力拉动小球,小球在碗壁上缓慢地滑动,细绳始终处于绷紧状态。小球从碗底中心点位置开始到接近碗口边缘A点的过程中,碗面对小球的支持力FN以及绳对小球的拉力FT的变化情况是

图5
( )
A.FN保持不变,FT不断变小
B.FN不断变小,FT不断变大
C.FN保持不变,FT先减小后增大
D.FN不断减小,FT先减小后增大
【应用示范】如图6所示,用水平力缓慢地拉动小球过程中,小球受到的支持力方向一直指向圆心O,绳对小球的拉力一直指向A,尽可能多画出几个位置的受力动态矢量图,由图可知FN不断变小,FT不断变大。B选项正确。

图6
【方法点拨】此法的关键在于“微”动态,即根据题设要求,将矢量进行微动态矢量作图,有时还需要注意变化过程中的特殊位置,要重点画出,再对整个变化的规律进行分析判断。
【小试牛刀2】如图7所示,不可伸长的轻绳AO和BO下端共同系一个物体P,且绳长AO>BO,A、B两端点在同一水平线上,开始时两绳刚好绷直,细绳AO、BO的拉力分别设为FA、FB。现保持A、B端点在同一水平线上,在A、B端缓慢向两侧远离的过程中,关于两绳拉力的大小随点A、B间距离的变化情况是

图7
( )
A.FA随距离的增大而一直增大
B.FA随距离的增大而一直减小
C.FB随距离的增大而一直增大
D.FB随距离的增大先减小后增大
【方法演练】初始状态BO竖直,所以BO绳拉力等于重物的重力mg,AO绳拉力为零。当B缓慢向右移动过程中,对于重力、AO绳的拉力FA、BO绳的拉力FB构成如图8所示的矢量三角形,作出几个位置的受力动态矢量图,由图8分析可知,AO的拉力FA随着B点向右移动一直增大,BO绳的拉力FB却是先较小后增大。AD选项正确。

图8
三、力的图示测量法
在高中阶段力的图示大多数在验证平行四边形实验后就很少应用,殊不知该方法用于力的平衡问题中题设所给的已知条件为具体数值,且数值运算相对复杂、结果也需要具体数值的选择题,采用力的图示在误差范围内结果相差不大,省去了用列表达式的数学运算,从而快速得到正确选项。
【应用示例3】某校物理课外小组神奇地用一个细绳套和两根轻牙签吊起一把汤匙,实验如图9所示。其中牙签P穿过细绳套置于水平桌面上,牙签Q上端撑在牙签P的左端,下端插入绳套打结点O处。汤匙的质量为30 g,稳定时测量可得细绳和牙签Q与水平方向的夹角分别为α=53°和β=37°,sin37°=0.6,cos37°=0.8,g=10 m/s2。对于装置研究可知
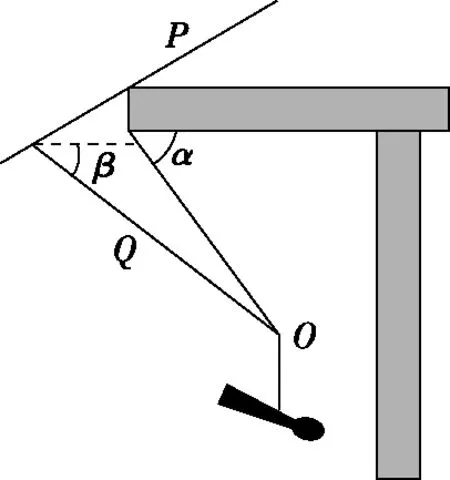
图9
( )
A.细绳承受的力大于牙签Q承担的力
B.细绳承受的力小于牙签Q承担的力
C.细绳承受的力为0.86 N
D.牙签Q承受的力为0.86 N
【应用示范】对结点O受力分如图10所示,因为整个系统处于平衡状态,重力、细绳承受的拉力FT、牙签Q所受的力FN三力构成一个闭合的矢量三角形,由此可知细绳承受的力大于牙签Q承担的力,A选项正确,B选项错误;重力mg=0.3 N,用刻度尺画出重力的矢量长度为3 cm(该长度只是一个标度值,要便于换算),细绳承受的拉力FT的矢量长度为8.6 cm,牙签Q所受的力FN的矢量长度为6.4 cm,根据比例关系换算可得,FT=0.86 N,FT=0.64 N,C选项正确,D选项错误。

图10
【方法点拨】此法仅适用于选择题,为了便于快速换算,要注意长度标度的选择,此方法关键在于作力的矢量图时要用直尺规范作图,只要规范作图,虽然有一定的误差,但选项间的数值相差一般不会太过于接近,这样基本可以按范围选中正确答案,快速秒杀。此法甚至可以推广到牛顿第二定律和一些矢量合成的选择题。
【小试牛刀3】由于卫星的发射场不在赤道上,同步卫星发射后需要从转移轨道经过调整再进入地球同步轨道。当卫星在转移轨道上飞经赤道上空时,发动机点火,给卫星一附加速度,使卫星沿同步轨道运行。已知同步卫星的环绕速度约为3.1×103m/s,某次发射卫星飞经赤道上空时的速度为1.55×103m/s,此时卫星的高度与同步轨道的高度相同,转移轨道和同步轨道的夹角为30°,如图11所示,发动机给卫星的附加速度的方向和大小约为
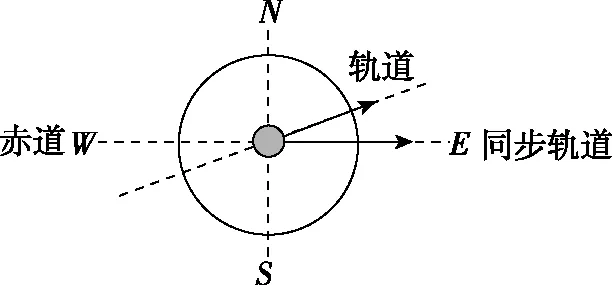
图11
( )
A.西偏北方向,1.9×103m/s
B.东偏南方向,1.9×103m/s
C.西偏北方向,2.7×103m/s
D.东偏南方向,2.7×103m/s
【方法演练】依题意可知同步卫星的环绕速度v1是卫星飞经赤道上空时的速度v2的二倍,转移轨道和同步轨道的夹角为30°,作出矢量图如图12所示,由图可知发动机给卫星的附加速度的方向东偏南方向;用刻度尺画出卫星飞经赤道上空时的速度v2的矢量长度为1 cm,即同步卫星的环绕速度v1的矢量长度为2 cm,量出发动机给卫星的附加速度Δv的矢量长度约为1.3 cm,故Δv=1.3×1.55×103m/s≈2.0×103m/s,B选项最接近该数值,故B选项正确。

图12
四、三力汇交原理法
在教学中发现学完力的平衡,有的人对三力汇交基本处于陌生状态,人教版教材对共点力的定力为:如果一个物体受到两个或更多力的作用,有些情况下这些力共同作用在同一点上,或者虽不作用在同一点上,但它们的延长线交于一点,这样的一组力叫做共点力,说明物体在不平行的三个力作用下时平衡,这三个力或其延长线必汇交到一点,简称为“三力汇交原理”。平时我们研究的对象多数可以看成质点或直接研究绳的结点,受到的力直接作用在同一点上,但类似有质量的杆或重力不可忽略的杆大多数不能看成质点,又因为力的合成的平行四边形定则只适用于共点力,就需要借助“三力汇交原理”来确定作用点,使共点力的平衡跃然纸上,就可以利用平行四边形定则或矢量三角形定则解决问题,难题就不难了。
【应用示例4】如图13所示,由密度分别为ρ1、ρ2(ρ1>ρ2)的两段长度相同的材料组成的细杆P一端放在水平地面上,另一端靠在固定于地面上的光滑半圆柱Q上,处于平衡状态,P与地面和Q的接触面点分别为M、N,半圆柱体Q的球心为O。现将细杆P翻转,使密度为ρ2部分置于N点,细杆P仍能保持静止状态,下列说法正确的是

图13
( )
A.细杆P翻转前在M点受到的摩擦力沿MN方向
B.细杆P翻转前在M点受到的支持力竖直向上
C.细杆P翻转后在N点受到的支持力大小不变
D.细杆P翻转后在M点受到的摩擦力变大
【应用示范】对细杆P受力分析可知细杆P翻转前在M点受到的摩擦力Ff沿水平向右,A选项错误;细杆P翻转前在M点受到的支持力FM竖起向上,B选项正确;把M点受到的摩擦力和M点受到的支持力合成为地面对M的作用力F,即细杆P受重力mg、地面作用力F、半圆柱体的支持力FN,因为ρ1>ρ2,所以细杆P受重力的重心作用点在ρ1段,根据三力汇交原理,细杆P受力如图14所示,三力构成闭合矢量三角形如图15所示,翻转后半圆柱体的支持力FN的方向不变,重力mg大小不变但其重心位置向上移动,地面对M的作用力F与水平面的夹角变小,此时F和FN的大小如图15中的虚线,即半圆柱体的支持力FN变大,C选项错误;由于地面对M的作用力F的水平分量为M点受到的摩擦力Ff,由图15可以看出翻转后摩擦力Ff变大,D选项正确。
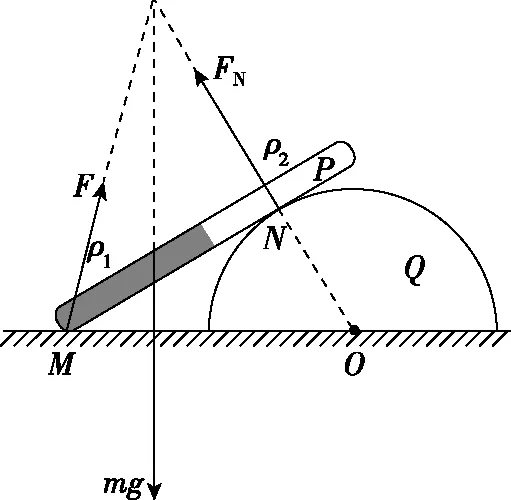
图14
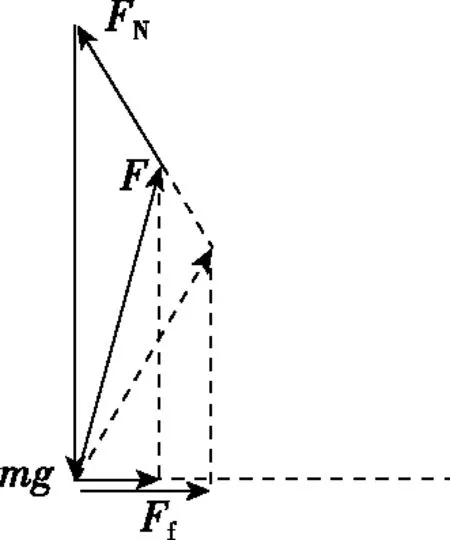
图15
【方法点拨】此法关键在于确定三力中两力的方向,然后通过三力汇交原理确定第三个力。
【小试牛刀】如图16所示,一根粗细均匀质量分布均匀的筷子AB,其质量为G,放在光滑的半径为R的半球形碗内,筷子与水平面成角θ=30°,假若筷子与两壁、碗边都没有摩擦力,则筷子AB的长度2l为
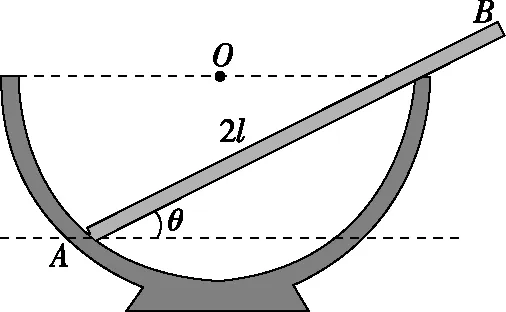
图16
( )
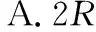
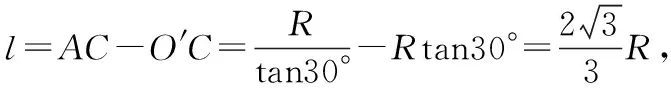

图17

