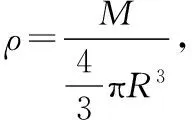点击高考热点 浅析天体运动
2020-11-18云南张西武
云南 张西武
天体运动是万有引力定律、牛顿运动定律、匀速圆周运动、向心力公式等力学规律应用的实例,也是历年高考的热点内容之一,通常出现在选择题中,它在力学中占有重要地位。综合分析近五年全国卷Ⅲ有关天体运动的考题。

真题示例题型及分析考点分析考查情景2016年全国卷Ⅲ第14题选择(6分)物理学史开普勒定律的发现史实2017年全国卷Ⅲ第14题选择(6分)万有引力定律的应用,飞船对接问题根据万有引力提供向心力,以此确定周期、线速度、向心加速度的表达式2018年全国卷Ⅲ第14题选择(6分)万有引力定律的应用根据万有引力提供向心力,考查地球不同卫星的周期比2019年全国卷Ⅲ第15题选择(6分)万有引力定律的应用根据万有引力提供向心力,以此确定线速度、向心加速度的表达式2020年全国卷Ⅲ第16题选择(6分)万有引力定律的应用根据万有引力提供向心力,结合黄金代换公式,考查线速度的表达式
由上表可以看出,命题者常以行星运动或是当年的太空活动为背景,通过卫星与中心天体等组成的系统,考查卫星与天体间运动的周期、角速度、线速度、向心加速度等物理量。解决此类问题的基本思路通常为:把某个卫星或天体绕另一个天体的运动看作匀速圆周运动,其所需的向心力由万有引力提供,并以此为基础确定卫星或天体与其中心天体间周期、角速度、线速度、向心加速度等物理参数之间的关系;当物体在星球表面时,若不考虑星球的自转,这时万有引力的大小等于重力的大小。
下面以天体运动为背景,谈谈高考中常见的几种考查类型。
一、对开普勒行星运动三大定律的考查类
【例1】长期以来,“卡戎星(Charon)”被认为是冥王星唯一的卫星,它的公转轨道半径r1=19 600 km,公转周期T1=6.39天。2006年3月,天文学家又发现两颗冥王星的小卫星,其中一颗的公转半径r2=48 000 km,则它的公转周期T2最接近
( )
A.15天 B.25天 C.35天 D.45天


对于开普勒第三定律的应用,需要注意以下几点:
1.适用范围
开普勒第三定律适用于一切的二体问题。其中,二体问题就是研究只有两个物体组成的系统问题,而忽略其他物体的影响,太阳系中的任何一个行星和太阳都可以近似看作是构成了一个二体系统。同时也适用于卫星绕着地球转。
2.比例系数k值确定
应用开普勒第三定律时,只有对同一个中心天体k值才相同。
二、考查宇宙速度类
【例2】如图1所示,是“嫦娥一号”奔月示意图,卫星发射后通过自带的小型火箭多次变轨,进入地月转移轨道,最终被月球引力捕获,成为绕月卫星,并开展对月球的探测。下列说法正确的是

图1
( )
A.发射“嫦娥一号”的速度必须达到第三宇宙速度
B.在绕月圆轨道上,卫星的周期与卫星质量有关
C.卫星受月球的引力与它到月球中心距离的平方成反比
D.在绕月圆轨道上,卫星受地球的引力大于受月球的引力
【解析】本题解题的关键是:①明白第三宇宙速度是指被发射物体能够脱离太阳系的最小发射速度,而“嫦娥一号”仍然没有脱离地球的引力范围;②知道万有引力的表达式以及什么力提供卫星做圆周运动的向心力。


(1)当v (2)当v1≤v 当被发射物体环绕中心天体做匀速圆周运动时,万有引力提供圆周运动的向心力。 (3)当v2≤v (4)v≥v3时,被发射物体将从太阳系逃逸。 【例3】我国高分系列卫星的高分辨对地观察能力不断提高。2018年5月9日发射的“高分五号”轨道高度约为705 km,之前已运行的“高分四号”轨道高度约为36 000 km,它们都绕地球做圆周运动。与“高分四号”相比,下列物理量中“高分五号”较小的是 ( ) A.周期 B.角速度 C.线速度 D.向心加速度 【例4】“天舟一号”货运飞船于2017年4月20日在文昌航天发射中心成功发射升空。与“天宫二号”空间实验室对接前,“天舟一号”在距离地面约380 km的圆轨道上飞行,则其 ( ) A.角速度小于地球的自转角速度 B.线速度大于第一宇宙速度 C.周期大于地球自转周期 D.向心加速度小于地面的重力加速度 【归纳总结】人造卫星的绕行速度、角速度、周期、向心加速度与半径的关系 需记住地球同步卫星的几个确定特征: (1)周期确定:T=24 h; (2)轨道平面确定:所有地球同步卫星的轨道平面都在赤道平面内; (3)运行速度确定:做圆周运动v=3.1 km/s; (4)运行高度确定:离地面高度约为36 000 km。 【例5】如图2所示,为地球卫星发射过程的示意图,先将卫星发射至近地圆轨道1,然后点火,使其沿椭圆轨道2运行,再一次点火,将卫星送入同步轨道3。轨道1、2相切于Q点,轨道2、3相切于P点,则当卫星分别在1、2、3轨道上正常运行时,以下说法中正确的是 图2 ( ) A.卫星在轨道3上的速率大于在轨道1上的速率 B.卫星在轨道3上的周期大于在轨道2上的周期 C.卫星在轨道1上经过Q点的速率大于它在轨道2上经过Q点时的速率 D.卫星在轨道2上经过P点的加速度小于它在轨道3上经过P点时的加速度 【例6】2019年春节期间,中国科幻电影里程碑的作品《流浪地球》热播。影片中为了让地球逃离太阳系,人们在地球上建造特大功率发动机,使地球完成一系列变轨操作,其逃离过程如图3所示,地球在椭圆轨道Ⅰ上运行到远日点B变轨,进入圆形轨道Ⅱ。在圆形轨道Ⅱ上运行到B点时再次加速变轨,从而最终摆脱太阳束缚。对于该过程,下列说法正确的是 图3 ( ) A.沿轨道Ⅰ运动至B点时,需要向前喷气减速才能进入轨道Ⅱ B.沿轨道Ⅰ运行的周期小于沿轨道Ⅱ运行的周期 C.沿轨道Ⅰ运行时,在A点的加速度小于在B点的加速度 D.在轨道Ⅰ上由A点运行到B点的过程,速度逐渐增大 【归纳总结】卫星变轨问题“四个”物理量的规律分析 (1)速度:如图4所示,设卫星在圆轨道Ⅰ和Ⅲ上的运行速率分别为v1、v3,在椭圆轨道Ⅱ上经过A和B点的速率分别为vA、vB。则卫星在A点加速,vA>v1,在B点加速,v3>vB,又因v1>v3,故有vA>v1>v3>vB; 图4 (2)加速度:因为在A点,卫星只受到万有引力作用,故不论从轨道Ⅰ还是轨道Ⅱ上经过A点,卫星的加速度都相同,同理,经过B点加速度也相同; (4)机械能:①在一个确定的圆(椭圆)轨道上机械能守恒。 ②若卫星在Ⅰ、Ⅱ、Ⅲ轨道的机械能分别为E1、E2、E3,则E1 【例7】假设“嫦娥三号”探月卫星到了月球附近,以速度v在月球表面附近做匀速圆周运动,测出运动周期为T,已知引力常量为G,不计周围其他天体的影响,则下列说法不正确的是 ( ) 【例8】“嫦娥四号”探测器于2019年1月在月球背面成功着陆,着陆前曾绕月球飞行,某段时间可认为绕月做匀速圆周运动,圆周运动半径为月球半径的K倍。已知地球半径R是月球半径的P倍,地球质量是月球质量的Q倍,地球表面重力加速度大小为g。则“嫦娥四号”绕月球做圆周运动的速率为 ( ) 【归纳总结】在求解中心天体质量、密度、第一宇宙速度等数据时,需根据题目所给的已知条件选择适当的计算方法,一般解题方法可分为以下两种:三、人造卫星及同步卫星的运行规律类


四、卫星变轨类





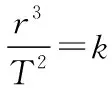
五、中心天体数据的计算