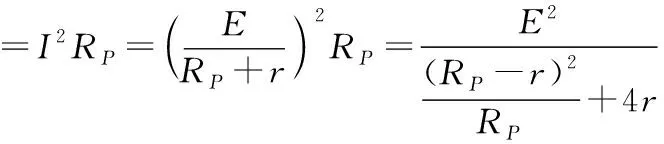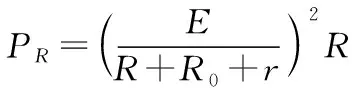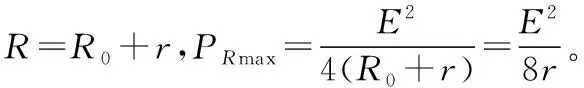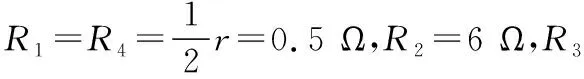电路中电源等效法之“形似”到“神同”
——等效法中的数学“换元”思想
2020-11-18广东陈施君
广东 陈施君
(作者单位:广东省佛山市三水区三水中学)
爱因斯坦相对论的基本原理告诉我们,无论你身在何处,或者你的行动速度如何,同一物理定律都会产生同样的效果。既然是这样,在保证效果相同的前提下,我们可以设法将陌生的、复杂的、难处理的问题转换成熟悉的、简单的、易处理的问题,这种方法称为“等效法”。等效法在处理多变量问题时可以减少变量个数,使学生更快捷、更准确地解决问题。我们可以把这种办法应用到电路分析中,把一部分有源电路等效为电源。等效电源模型是电学中一类十分重要的物理模型,但在应用等效法解决电学问题时,学生往往胡乱套用,问题根源在于他们不理解“等效法”的本质含义,所以本文将从数学“换元”思想切入,启发学生深刻理解“等效法”,以求做到灵活、准确运用“等效法”处理复杂电学问题。
解数学题时,把某个式子看成一个整体,用一个变量去代替它,从而使问题得到简化,这叫换元法。换元的实质是转化,关键是构造元和设元,理论依据是等量代换,目的是变换研究对象,将问题转移至新对象的知识背景中去研究,从而使非标准型问题标准化、复杂问题简单化,变得容易处理。而物理中等效法的本质理解就是数学的“换元”思想,要深刻理解等效法的本质,必须从数学逻辑推导中寻找答案,深入理解从“换元”到“等效”的转换。
一、伏安法测电源电动势与内阻误差分析中的等效换元
1.对电源来说,电流表外接法,如图1所示
如图1乙所示,U=E测-Ir测①


图1
对比①②两式,构造元,进行数学换元
U=E测-Ir测③
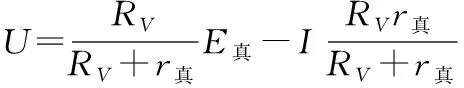
即U=-IΔ

回归到物理意义理解,根据并联电路特点,其实就是把电压表与电源并联等效为一个新电源,实验所测出的电动势等效为电压表与电源并联后的路端电压,测出的内阻等效为电压表内阻与电源内阻并联的新电阻,路端电压小于电动势,并联后电阻小于任一并联支路电阻,分析出误差情况E测 怎么找出这一等效思想呢?关键是把测量情况和修正后的真实情况对应的物理规律式进行数学函数式的相应变换,让变换后的式子结构形式相同,再从里面找出对应的部分,就可以得出换了的那部分“元”。数学函数式的形式相同,从物理上讲,就是规律相同,这就是等效法的前提,而同一物理定律会产生同样的效果,所以数学上的“换元”就是等效法的本质理解。 2.对电源来说,电流表内接法,如图2所示 如图2乙所示,U=E测-Ir测① 考虑到电流表分压作用所引起的误差,现对上式进行修正 如图2甲所示,U+IRA=E真-Ir真 图2 整理得出变式U=E真-I(RA+r真) ② 对比①②两式,构造元,进行数学换元 同理,发现E测将E真换元,r测将RA+r真换元,结果就是E测=E真,r测=r真+RA,直接得出误差分析E测=E真,r测>r真。 回归到物理意义理解,根据串联电路特点,其实就是把电压表与电源串联等效为一个新电源,实验所测出的电动势等效为电流表与电源串联后的路端电压,测出的内阻等效为电流表内阻与电源内阻串联的新电阻,路端电压等于电动势,串联后电阻大于任一串联部分电阻,所以误差情况为E测=E真,r测>r真。 非线性元件的特点是对应不同的电压,有不同的电流值,当把它接入电路中,如何求出最后非线性元件在电路中的电阻值呢? 【例1】由某种材料制成的电器元件,其伏安特性曲线如图3所示。现将该元件接在电动势为8 V,内阻为4 Ω的电源两端,通过该元件的电流为________A,该元件消耗的电功率为________W。 图3 【解析】对元件有U=IR① 对电源有U=E-Ir② 对于①式,结合该元件的伏安特性曲线,从数学角度来说有三个变量,其中U和I与②式中的U和I是相同的变量,也就是说此方程组中,有三个变量是未知的,以高中生现有的数学知识储备来说,不能通过该方程组来解出结果,只能换个方法,利用图像中的两式对应的图线交点找出它们的共同解。 具体做法是:将该元件接在电动势为8 V,内阻为4 Ω的电源两端,根据闭合电路欧姆定律得U=E-Ir,带入数据得U=8-4I,作出电源的外特性曲线,则两图线交点即为该元件接在电源上的工作状态,由图4可知,I=1 A,U=4 V,此时该元件消耗的电功率为P=UI=4 V×1 A=4 W。 图4 例1给出了我们解决此类问题的常用办法,那当我们遇到例2时,又如何理解等效法处理的本质呢? 【例2】某元件的伏安特性曲线如图5所示,若将两个这样的元件串联后与电动势E=3.0 V、内阻r=2 Ω的电源连接,下列说法正确的是 图5 ( ) A.此时该元件的电阻约为0.8 Ω B.此时该元件的电阻约为1.3 Ω C.此时该元件的功率约为1.8 W D.此时该元件的功率约为0.55 W 例2的物理情景与例1基本一样,区别是例2是两个元件和电源串联在一起,是两个,而例1是一个,那如何进行例1到例2的等效呢? 【解析一】如图6所示 图6 对两个元件2U=I·2R① 即U=IR② 对电源2U=E-Ir③ 构造元,进行数学换元 例2与例1的数学函数式结构形式上是一致的,可以把例1的方法沿用到这里,也是从两个方程对应的图线交点找到答案。 ①式等效为原来题目中图线,只需要在原图上画出④式对应的图线,它们的交点就是此时元件的电流、电压值,此交点为(0.65 A,0.85 V),从而根据③式得出该元件此时的电阻约为1.3 Ω,功率约为0.55 W,即BD选项正确。 再细细观察,就会发现,在数学推理过程中,由①②式变到③④式,其实就是两个元件与电源串联,等效为一个元件与电源的一半串联成为两个独立电路,问题就可以等效到求一个元件与电动势为1.5 V,内阻为1 Ω的电源串联时对应的元件电阻,功率求解问题。 【解析二】构造元,进行数学换元 当然,也可以做出以上等效,物理意义就是把两个元件等效为一个2R的元件,再与电源串联,但在用图像法求解问题时需在原题U-I图线上逐个将同一个电流对应的电压放大两倍来描点,得出2R元件的新图线,再画④对应的图线,找出它们的交点。但这样做不好,因为元件的伏安特性曲线是弯曲的,逐个描点作法麻烦而且不够准确,得出结果也一样有误差,而且,结合题目原图坐标如图5所示也发现,找不到3.0 V的点,所以这种做法不可取。这也说明,在选择如何等效的方法上,仍需要比较哪种方法能更简捷准确地解决问题。 电源的最大输出功率 图7 当RP=r时,P出有最大值,即电源此时输出功率最大。 作出电源输出功率随外电阻阻值变化的图像,就可以直观地体会到其中的变化特点。 P出与RP的关系如图8所示。 图8 【例3】如图9所示,电源内阻为r,定值电阻R0=r,可变电阻R的最大阻值为2r。求: 图9 (1)R上消耗的最大功率PR (2)R0上消耗的最大功率PR0 【解析】构造元,进行数学换元 (1)R上消耗的功率 可是解决第二问,就不能像第一问那样进行换元等效了,因为R0上消耗的最大功率 虽然表面结构形式与③类似,但R0却是个定值,变量只有R,且处在分母上,而③式上的变量RP既在分子上,亦处于分母中,因此两式本质上是不一样的,不能用等效电源法,④式子中当R减小时,PR0增大,当R等于零时,PR0最大。而③式子中分子、分母有同样的变量RP,当RP减小或增大时,很难立即确定P出的变化情况,只能通过进一步变换函数式得出极值。 第二问的解决过程给我们一个启示即想等效换元,必须两函数式的形式要完全一致,变量一致,运算法则一致。 图10 【解析】构造元,进行数学换元 设R=R1+R4+r 再把R3抽出来,上式可变为 代入数据得出r′=1.5 Ω 此时画出对应的等效电路图,如图11所示 图11 沿用例3中③式结论,当滑动变阻器阻值等于1.5 Ω时,滑动变阻器的消耗功率最大,也就是在滑动变阻器R3的滑片K由最下端向最上端滑动过程中,滑动变阻器的消耗功率先变大后变小。
二、等效电源之非线性元件接入电路问题中的“换元”思想

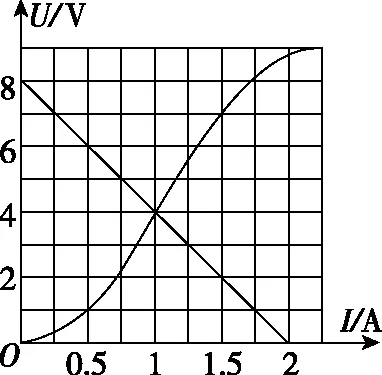
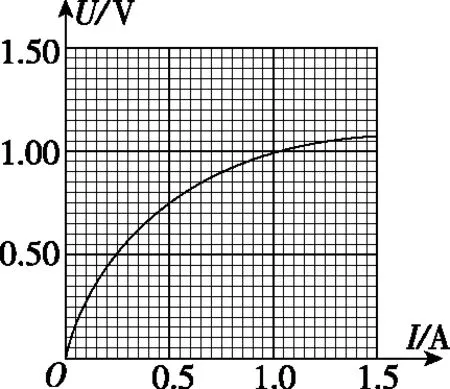




三、等效电源之最大功率中的“换元”思想