研发活动对中国工业绿色生产率的驱动机制研究

程淑平，孟令杰，刘宏伟

(1.南京理工大学 经济管理学院，江苏 南京 2100942;2.安徽大学 商学院，安徽 合肥 230031)

长期以来，中国工业“三高一低”的粗放式增长对资源环境造成了巨大压力，并引发了雾霾等一系列严重的污染问题。为解决工业经济增长与资源环境之间日益突出的矛盾，绿色、低碳的经济发展方式势在必行。而实现这一发展方式的核心动能在于创新。随着中国经济步入“新常态”，创新被提升到“支撑引领”的战略地位。与之相应，我国研发投入保持了高速增长的态势。2013年全国研发经费总量首次跃居世界第二位，此后保持了年均两位数的增长率，到2018年，全国研发经费支出达到19 677.9亿元，占GDP的比重为2.19%，投入强度已达到中等发达国家水平[1]。如此高强度的研发投入是否促进了工业绿色增长，其影响机制如何，是值得深思的问题。同时，研发投入并不是研发活动影响绿色经济增长的唯一路径，在投入既定的情况下，通过优化研发资源配置，提高研发资源利用效率，亦会对工业绿色增长产生积极作用。基于此，本研究以绿色经济增长的核心指标——绿色生产率为落脚点，利用2008～2017年中国工业企业省级面板数据，分析研发投入、研发效率对绿色生产率的异质性影响，在此基础上，探讨当前研发创新活动对工业绿色发展的驱动是“研发投入数量驱动型”还是“研发效率驱动型”，其研究结论将为科学设计创新驱动发展路径提供有益的参考。

一、文献综述

研发活动是企业技术创新的核心内容，其对生产率的作用机制受到了学者们的广泛关注，并取得了丰富的研究成果[2-5]。然而，上述学者们在测度生产率时，仅考虑经济产出，忽略了环境污染等非期望产出，其得出的结果并不能反映真实的工业生产关系。历史经验表明，片面追求经济增长，会带来严重的生态环境问题。由此，将大气污染、水污染等非期望产出纳入生产率分析框架，考虑资源环境约束下的绿色生产率增长，成为近年来学者们关注的焦点[6]。关于绿色生产率的驱动机制，多数学者认可研发活动扮演着决定性的作用[7-8]，相关的研究也取得了一定的成果，但也存在明显的不足。从研发投入角度来看，直接考察研发投入对绿色生产率的驱动机制的文章较少，得出的结论也不一致。Li等人运用系统矩估计和面板分位数回归方法考察了2005～2015年中国绿色生产率的创新驱动机制，发现研发投入显著促进了工业绿色增长，且该促进作用在资源节约和污染减排方面更为有效[9]。Lu等人以2004～2016年中国省际面板数据为研究对象，分析了绿色生产率的驱动因素，结果表明，研发投入对绿色生产率的影响并不显著，且存在区域差异性[10]。更多学者是将研发投入作为中介或调节变量，考察环境规制、政府补贴、对外开放等因素对绿色生产率的影响。如Wang等人对OECD国家工业部门的研究显示，当环境规制强度低于平均值时，研发投入与环境规制的交互项对绿色生产率有积极影响，而当环境规制强度超过平均值时，该交互项的作用为负[11]；谢荣辉运用两阶段模型分析环境规制、研发投入与工业绿色生产率之间的关系，发现环境规制引致的创新投入能显著促进绿色生产率的提升[12]；王昀和孙晓华考察政府补贴对绿色生产率的作用机制时，发现其传导路径研发投入系数显著为负，说明研发投入的增加不仅没有带来绿色生产率的提升，反而产生了抑制作用[13]；刘启雷等人实证研究发现，FDI与研发投入的交互项显著提升了环境技术水平[14]。从研发效率视角来看，当前尚未有文献单独考察研发效率对绿色生产率的影响机制。

梳理文献可知，学者们主要基于中介或调节作用考察研发投入对绿色生产率的影响，其对两者间作用机理的刻画较为单薄，缺乏深入分析，得出的结论存在不一致性，且尚未有文献同时考察研发投入、研发效率对绿色生产率的驱动机制。基于此，本文拟分析3者间作用关系，并通过计量模型加以验证。

二、机理分析与模型设定

内生经济增长理论认为，技术创新是经济增长的源泉，而研发活动则是技术创新的核心内容。在资源日益紧缺，生态环境日趋恶化的形势下，加大研发投入，提升技术创新能力，成为当前推动经济发展方式转型的首要选择。事实上，研发活动对绿色生产的影响具有双重性，也就是通常所说的“双刃剑效应”。

从研发投入来说，随着研发人员和研发经费的不断增加，技术创新活动不断增多，新知识、新技术对生产率的推动作用亦随之增强。这里的生产率指的是一般意义上的生产率，并非资源环境约束下的绿色生产率。绿色生产率同时包含了期望产出和非期望产出，不仅考量了经济利益，还将资源环境效益纳入分析框架中，以谋求经济与生态的协调与可持续发展[15]。考虑到绿色生产率目标结构的双重性，研发投入对其影响机制就显得更为复杂。基于此，将研发投入引致的技术创新分为绿色技术创新和非绿色技术创新。一方面，绿色技术创新可以通过末端治理和前端预防两种途径促进工业绿色增长。其中，末端治理指的是对各类污染排放物的回收与再利用。先进的回收分解技术，能有效减少污染物排放，促进废弃物再利用，在降低企业生产成本的同时，实现了物质资源的节约。前端防御指的是在产品生产的整个过程中控制污染物的产生和排放。具体分析如下：在生产上游阶段，通过绿色技术创新，使用更加节约和高效的新材料，并降低或消除原材料中的有毒、有害成分；采用更加清洁的能源(如天然气、太阳能、风能等)替代传统高碳能源(如煤、石油等)，加强环境友好型和可再生能源的应用；优化产品设计，创新出轻量化、节能、易回收、高品质的环保产品。在产品生产阶段，充分利用智能生产，改进设备与工艺流程，淘汰或替代传统落后的技术，提高资源利用的有效性，从而节约资源，减少浪费。例如，通过使用超低排放燃煤发电技术，至2018年，我国累积减少粗钢3 500多万吨，淘汰煤炭落后产能2.7亿吨[16]。另一方面，非绿色技术创新，特别是基于“污染”的创新，可能给绿色增长带来不利的影响。非绿色技术创新主要是以人力节约和资本节约为基础，企业为了实现利润最大化，热衷于追求这一类的创新，而选择性忽视其可能存在的负面环境影响。在非绿色创新中，部分创新成果虽然带来了人力、物力的节约，促进了经济效益，但同时也造成了较为显著的环境污染。如洗衣粉的广泛使用增加了工业生产，但同时也导致了水质恶化和湖泊的富营养化问题。另有部分创新成果虽然在产品使用阶段是环保的，但是其生产阶段可能会造成环境污染。例如，页岩气的大规模开采和应用有助于缓解能源短缺，降低我国工业经济发展成本，但页岩气开采过程(特别是水力压裂活动)消耗了大量的水资源，并给当地的地质环境造成了威胁。过于追求非绿色创新可能会产生技术的“回弹效应”，造成资源浪费和污染加剧。从这一视角看，技术创新在某种程度上不利于工业绿色生产率的提升。综合而言，研发投入对工业绿色增长的影响，取决于上述两种类型技术创新的综合作用结果，其影响方向是不确定的。

从研发效率来看，研发效率提升，意味着投入既定的情况下，可以通过优化资源配置，提高创新资源利用的有效性，取得更多技术创新成果。而该创新成果依然可能是绿色技术创新，亦可能是非绿色技术创新，研发效率提升对绿色生产率的影响取决于二者作用的综合结果，方向也是不确定的，有待于实证检验。

此外，学者的研究表明，研发创新活动具有较强的空间外溢作用[17-18]。也就是说，地理空间临近使得地区间更容易产生人员信息交流，从而促进创新活动的扩散。不考虑空间相关性的传统计量模型得出的结果可能是有偏误的。从计量方法上来说，是否采用空间计量模型需要对变量进行空间相关性检验，主要的检验方法是莫兰指数法。

若空间相关性显著，则可考虑的空间计量模型主要包括4种，一是只包含因变量空间滞后的空间自回归模型(SAR模型)；二是只包含空间误差自相关的空间误差模型(SEM模型)；三是同时考虑因变量和自变量空间滞后的空间杜宾模型(SDM模型)，四是同时考虑因变量空间滞后和误差项自相关的空间自相关模型(SAC模型)。上述4种模型，各有其适用性，具体选择哪一种，还需要进行相关检验。式(1)、式(2)分别是研究设计的空间杜宾模型和空间自相关模型：

Yit=β0+δWYit+β1inputit+β2effcyit+β3Xcontrol+θ1Winputit+θ2Weffcyit+θ3WXcontrol+εit

(1)

Yit=β0+δWYit+β1inputit+β2effcyit+β3Xcontrol+uitμit=λWμit+εit

(2)

对式(1)附加一定限制条件，令θi=0，即可得到SAR模型；令θi+δβi=0，即可得到SEM模型。同理，对式(2)施加一定的限制条件，令λ=0，即可得到SAR模型，令δ=0，即可得到SEM模型。SAR和SEM模型分别如式(3)、式(4)所示：

Yit=β0+δWYit+β1inputit+β2effcyit+β3Xcontrol+εit

(3)

Yit=β0+β1inputit+β2effcyit+β3Xcontrol+uit；

uit=λWuit+εit

(4)

若空间相关性不显著，则令(1)中的所有空间项系数均为0，模型退化为经典的OLS模型，如公式(5)所示：

Yit=β0+β1inputit+β2effcyit+β3Xcontrol+εit

(5)

其中，Yit为工业绿色生产率；inputit为研发投入；effcyit为研发效率；Xcontrol为一系列控制变量，模型中绝对数表示的变量均进行对数处理。值得注意的是，工业绿色生产率是截断数据，故在模型中也做了对数处理。W表示空间权重矩阵，研究采用邻接矩阵对变量的空间相关性进行考察，其计算方法为：两地区若相邻，则权重取值为1，否则为0。uit、εit表示随机扰动项，且满足：uit～iid(0,σ2)，uit～iid(0,σ2)。

三、变量测度与数据来源

1.变量测度

绿色生产率的测度是典型的多投入多产出问题，非参数的DEA方法在这一领域具有独特的优势而被广泛运用。基于实际决策需求，拟选用Huang 等人提出的US-SBM模型[19]。该模型允许效率值大于1，也不要求投入、产出变量同比例变动，较好地满足实际要求。模型设定如下：

假设有n个决策单元，每个决策单元都有投入X，期望产出Yg和非期望产出Yb，其中，x∈Rm、yg∈Rs1、yb∈Rs2，得出的分式规划模型为：

λ,s-,sg,sb≥0

(6)

公式(6)中，sg、sb分别表示期望产出、非期望产出的松弛量；ε为非阿基米德无穷小量；λ表示权重向量；ρ*是目标效率值，当ρ*< 1时，表示决策单元是无效率的，反之则表示决策单元是有效的。

上述方法测算的效率值是相对的，不能进行跨期比较，为克服这一问题，采用可比较、可传递的GML方法进一步测度绿色生产率。其基本思想是将所有各期的总和作为共同参考集，构造出如下所示全局指数：

(7)

公式(7)中Eg(xt,yt,bt)、Eg(xt+1,yt+1,bt+1)分别表示相邻两个时期t，t+1期的生产效率。GML指数即为共同前沿面下两个时期生产效率值之比。若该比值大于1，表示从t期到t+1期的绿色生产率是增长的；若该比值等于1，表示从t期到t+1期的绿色生产率没有发生变化；若该比值小于1，表示从t期到t+1期的绿色生产率是下降的。需要指出的是，测算出的GML指数值反映的是绿色生产率的增长率。绿色生产率的水平值计算如下：以2008年效率值为基期累乘各期指数。

绿色生产率测度的具体指标如下表所示：

表1 工业企业绿色生产率评价指标体系

研发投入主要测度指标为：研发经费内部支出和研发人员全时当量，运用熵值法将两者合成为一个综合性的投入指标。

研发效率同样采用非参数的DEA方法进行测度，其投入变量主要是研发资本和研发人员全时当量，产出变量包括：专利申请数、专利授权数和新产品销售收入。

控制变量：为消除其他因素对工业绿色生产率可能造成的影响，选取如下控制变量：①经济发展水平(agdpit)，用人均gdp测度，为验证环境库兹涅茨曲线在中国是否存在，在计量模型中加入agdpit的二次项；②产业结构(strit)，用第三产业占比测度；③市场化水平(marktit)，用私营企业总资产占比测度；③区域开放水平(openit)，用年度实际进出口总额测度；④人力资本水平(eduit)，用每万人在校大学生人数测度；⑥基础设施状况(infit)，用邮电(邮政和电信)业务总量测度。

2.数据来源

本文采用2008～2017年中国30省份(数据不包括西藏和港澳台地区)省级面板数据考察研发投入、研发效率与工业绿色生产率之间的关系。数据主要来自中国统计年鉴、中国工业统计年鉴、中国环境统计年鉴。具体来说，在工业绿色生产率测度体系中，劳动投入和资本投入统计指标来自中国工业统计年鉴；能源投入与期望产出统计指标来自中国统计年鉴；非期望产出统计指标来自中国环境统计年鉴。此外，研发投入和研发效率统计指标均来自中国科技统计年鉴。由于西藏地区数据缺失较为严重，在实证分析中剔除了该省份。表2报告了变量的描述性统计分析情况，主要包括样本数个数、均值、标准差、最大值与最小值等。考虑到研发投入和研发效率可能存在多重共线性问题，表2还列出了各解释变量的方差膨胀因子值(Variance Inflation Factor,VIF)，从中可以看出，解释变量中VIF最大值为3.169，小于临界值10，故可认为模型的解释变量不存在严重的多重共线性问题。

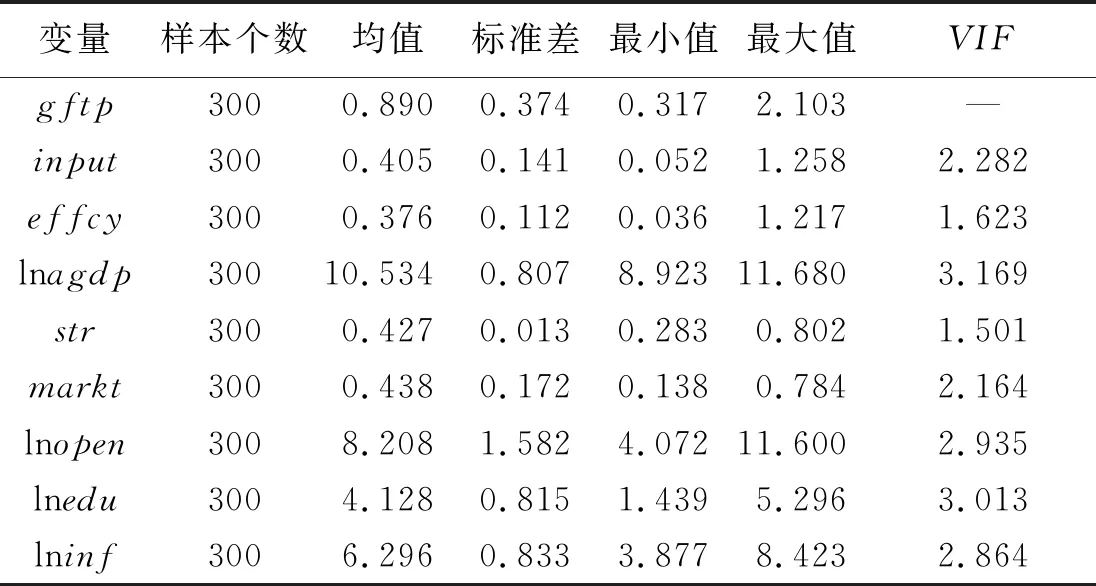
表2 各变量的描述性统计分析结果

四、实证结果分析

1.结果分析

Moran’I指数检验结果显示，研发活动存在显著的空间相关性。具体表现为：研发投入除2008年和2009年外，Moran’I指数均在10%以上的水平显著；研发效率除2009年以外，Moran’I指数均在5%以上的水平显著。因此，选择空间计量模型是合适的，可以提高分析结果的准确性。

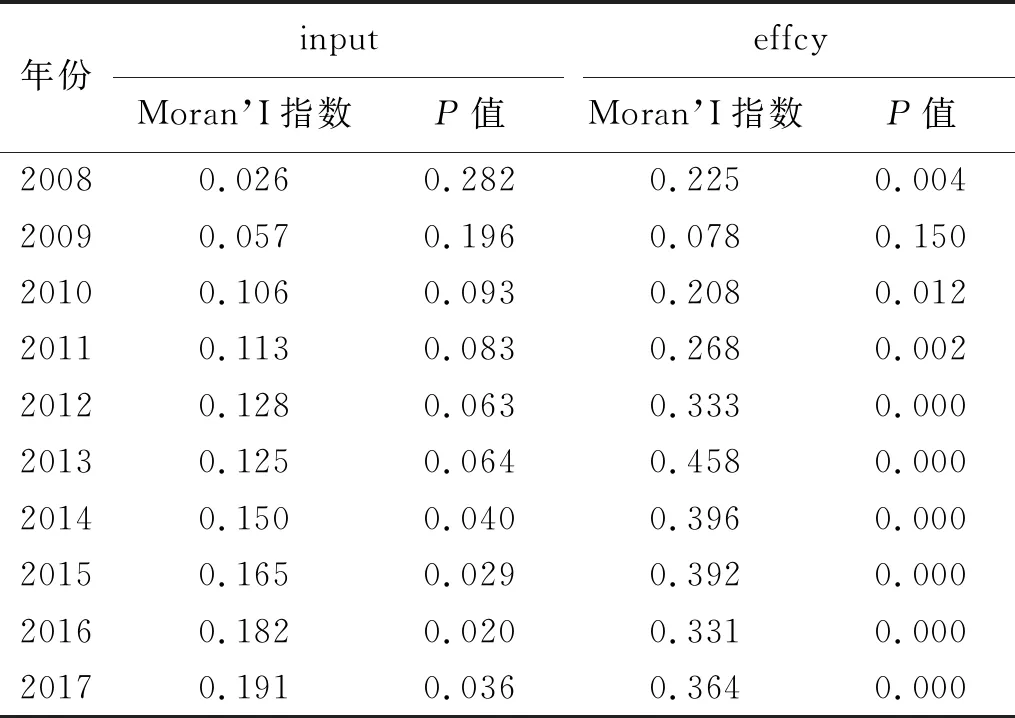
表3 研发活动Moran’I指数检验结果

由前述分析可知，可供选择的空间面板计量模型主要有SAR、SEM、SDM和SAC，按照Anselin 等人提出的判断准则，选取Log-L、LR和Wald对模型的拟合效度进行检验，以判断哪种模型更为适用[20]。进一步经hausman检验，空间面板模型均选用固定效应。各模型回归估计结果如表4所示。

表4 空间面板模型回归估计结果

可以看出，表4中3类空间面板模型的空间项系数为正，除SAC外，均通过10%的显著性检验。从模型的拟合效果来看，SDM模型较其他3种模型具有回归系数显著个数最多的特点，初步考虑选择该模型。接下来要进一步检验SDM模型能否退化成SAR模型或SEM模型，使用的检验方法是LR检验和Wald检验。LR检验统计量和Wald检验统计量均服从自由度为K的卡方分布，该检验的原假设是：H0：θ=0和H0：θ+δβ=0，若两者都被拒绝，则说明SDM模型不能退化为相应的空间滞后模型或空间误差模型。检验结果如表5所示，LR空间滞后检验、LR空间误差检验、Wald空间滞后检验、Wald空间误差检验均在1%的水平上拒绝原假设，说明选择SDM模型是合理的。

表5 SDM模型的Wald和LR检验结果

从SDM模型分析结果来看，工业绿色生产率的空间交互项显著为正，说明本地区的工业绿色增长会受到临近地区工业绿色生产活动的加权影响。临近地区的工业绿色增长对本地区有正向的空间溢出效应。研发投入对工业绿色生产率的影响为负，但不显著可能的原因有两点：一是当前我国工业企业仍然是以盈利为第一目标，在研发创新活动中过于追求经济利益而忽视了资源环境问题。二是内生增长理论认为，研发投入初期，存在“站在巨人肩膀效应”，这一时期产生的绿色技术创新知识和技术往往是最容易被发现的，随着创新过程的持续推进，逐步出现“竭泽而渔效应”，新的创意产生进而推动生产力发展变得更加困难。两者的相互作用可能使得研发投入对工业绿色增长产生非线性影响。非线性影响的存在也可能导致两者间线性关系的不显著。研发效率及其空间交互项对工业绿色生产率均有显著的正向影响。说明投入既定的情况下，提升研发效率能有效促进我国工业绿色增长，并且临近地区研发效率会对本地区产生正向的空间溢出效应。综合而言，当前我国工业绿色增长创新驱动机制已经是“效率驱动型”而非“数量驱动型”，对研发活动应逐步摆脱“R&D投入迷信”，进而转到研发活动提质增效上来，通过优化创新资源配置，提升工业绿色生产率。

从控制变量来看，人均收入与工业绿色生产率存在显著的“U”型关系，即随着人均GDP的增加，工业绿色生产率呈现出“先抑后扬”的增长趋势。这一结论验证了环境库兹涅茨曲线在我国的存在。具体来说，在低收入阶段，工业经济增长方式较为粗放，导致了大量的资源消耗和污染排放，绿色生产率降低。随着人均收入的不断增长，资源与优质环境变得日渐稀缺，政府环境规制政策加大，迫使工业企业不断改进生产技术，转变增长方式，节约资源，减少污染排放，最终改善环境质量。产业结构与工业绿色生产率呈现出显著的正相关关系。说明大力发展第三产业，促进产业结构高级化，有助于提升我国工业绿色生产率。市场化水平与工业绿色生产率负相关。可能的原因在于，度量市场化水平的指标主要是私营企业总资产占比。私营经济越活跃，市场化水平越高。尽管私营企业相对于国有企业有着较高的生产率水平，但是，在污染防治方面，国有企业更容易响应政府的号召，也有更多的资源和技术进行环境治理投资。私营企业往往规模较小、实力薄弱，无力承担环境治理成本，因而绿色生产率相对较低。对外开放水平与绿色生产率呈现出显著的负相关关系，验证了“污染天堂”效应在我国的存在性。说明当前外商在我国投资设厂，主要是转移本国污染密集型企业，资源消耗大的低端产业，考虑到我国环境质量日趋恶化的客观现实，制定相关政策，优化外商投资结构势在必行。人力资本水平和基础设施影响不显著，不再赘述。

表6 研发投入带二次项的空间面板模型回归估计结果

由上文分析可知，研发投入与绿色生产率之所以存在不显著的负相关，可能是由于二者间非线性关系所致，为证实这一猜想，在空间面板模型中加入研发投入的一次项和二次项，其分析结果如表5所示。参考前文分析方法，初步选择SDM模型进行分析。进一步的LR和Wald检验表明，两个统计量均在1%的水平上显著拒绝原假设，也就是说，SDM模型不能转化为等价的SAR或者SEM模型。故最终确定SDM是较为合适的计量模型。从模型分析结果可以看出，研发投入与工业绿色生产率之间存在显著的“倒U型”关系。在研发投入初期，研发投入的增加促进了工业绿色生产率的提升，当研发投入达到某一水平时，出现了“拐点”效应，研发投入的增加导致了工业绿色生产率的下降。可能的原因在于工业绿色技术创新的“竭泽而渔效应”。此外，研发投入过多产生的“拥挤效应”也不利于工业绿色增长。从空间溢出效应来看，由于同时存在一次项和二次项，其作用方向具有不确定性。

表7 基准模型稳健性检验结果

2.稳健性检验

本文主要从以下3个方面对基准模型进行稳健性检验。(1)用经济距离矩阵替换邻接矩阵，其回归结果如模型(9)所示；(2)缩减样本的时间范围，参考葛鹏飞等人的做法[21]，剔除2008、2017两个年份，仅使用2009～2016年各省份数据，回归结果如模型(10)所示；(3)运用AHP方法替换熵值法重新构建研发投入综合指标，用超效率方法替换US-SBM方法测量研发效率，回归结果如模型(11)所示。可以看出，各模型虽然系数大小有所变化，但是系数方向和显著性水平未发生根本性改变，因此分析结果是稳健和可靠的。接下来对带二次项的模型亦进行相同的稳健性检验，结果也是可靠的，不再赘述。

3.研发投入的门限特征检验

(1)门限模型设定

研发投入和工业绿色生产率之间存在非线性关系。为详细分析变量间关系的阶段性演化特征，采用Hansen于1999年提出的门限回归方法设计模型，门限回归模型的优势在于分阶段考察变量间的关系形式，并能有效测算出关系形式发生变化的“拐点”。考虑到变量存在的空间相关性，直接使用面板门限模型可能造成结果偏误。借鉴孙建的空间过滤方法[22]，将变量可能存在的空间依赖性进行去除，对过滤后的数据进行门限回归分析，单门限计量模型如下：

effcyit=α1+β11inputit·I(qit≤γ1)+β12inputit·I(qit>γ1)+β2Xcontrol+εit

(8)

公式(8)中，I(*)表示示性函数，当括号内不等式成立时取值为1，不成立时取值为0；qit为门限变量，公式(8)中的门限变量为研发投入；γ1为待估计门限值；其他变量与前述模型相同，εit表示随机扰动项；i表示省份；t表示年份。公式(8)表述的是单门限回归模型，多门限回归模型以此类推。

(2)门限效应检验

首先检验研发投入与工业绿色生产率之间是否存在门限效应。分析结果如表8所示，可以看出，研发投入存在单门限效应，门限值为0.816，且在0.05的水平上呈现出显著性，双门限效应不显著。

表8 门限效应估计

图2显示了单门限模型得到的似然比统计量LR与门限参数图，水平虚线为95%置信区间下的LR临界值。LR曲线最接近0的点就是门限估计值。LR检验曲线与水平虚线交叉点形成的区间即为置信区间。当门限值落在该置信区间内时，门限值是有效的。依图1所示，模型的门限值落在95%的置信区间内，因而单门限效应是显著的。

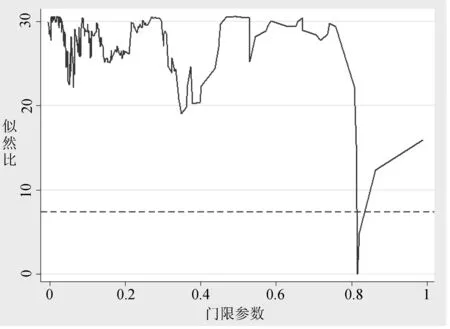
图1 研发投入门限效应似然比检验图

(3)门限回归结果分析

表9报告了门限模型回归分析结果，控制变量不再列出，可以看出,当研发投入小于0.816时，增加研发投入有助于提升工业绿色生产率，当研发投入大于或等于0.816时，增加研发投入反而不利于工业绿色增长(模型系数由1.012转为-0.693)。值得注意的是，河南、山东两省出现在门限值左侧附近(2017年研发投入均接近0.800)，应注意合理控制其研发投入强度，防止越过拐点而对绿色生产率产生不利影响。

表9 门限回归分析结果

五、结论与启示

运用US-SBM模型与GML指数相结合的方法，测度包含非期望产出的工业绿色生产率。在此基础上，采用空间面板计量模型考察研发投入、研发效率对工业绿色生产率的影响机制。分析结果表明，研发投入与工业绿色生产率之间存在显著的“倒U型”关系，随着研发投入的增加，工业绿色生产率呈现出“先扬后抑”的趋势特征。过度追求研发投入不利于工业绿色增长。研发投入的空间溢出效应显著，但作用方向不明确。研发效率对工业绿色生产率存在显著正向影响。在研发投入既定的情况下，提高研发资源利用效率，优化各类资源配置，更有利于工业绿色生产率的提升。同时研发效率存在正向空间溢出效应，相邻地区可通过研发人员交流与学习，提升本地区的工业绿色生产率。上述分析结果说明当前我国工业绿色增长应更为注重“研发效率驱动机制”，而不是一味追求研发投入的“攀比式增长”。

研究的启示在于：研发创新是走资源节约型、环境友好型发展道路的核心动能，同时也是工业绿色、低碳转型的重要着力点。当前地方政府的科技研发支持还存在着盲目的“研发投入崇拜”，即片面追求研发投入数量增长，而忽视研发效率提升。研究结果显示，过度的研发投入会对工业绿色增长产生“过犹不及”的影响，而研发效率却能显著推动绿色生产率增长。因此，可以从以下3个方面提升研发效率。

(1)建立健全政府研发资助的监督管理机制。一是设定分级目标管理体系，对于高水平、原创性符合市场需求的创新项目予以重点支持，对于低水平、结构同质的创新项目予以限制。二是构建并完善预算管理控制系统，规范研发资金使用流程，防止资金浪费和滥用。三是引入第三方评估机制，对创新项目进行公平客观的评价，防止因后期考核薄弱而导致各种寻租行为。

(2)完善产学研协同创新机制。一是要构建合理的风险分担与利益共享机制。制度化确定各主体的责任、权利与义务，以减少合作过程中相互推诿、利益纠纷现象，也为合作的系统性、持久性奠定良好的基础。二是强化企业的主体地位。企业在产学研合作中应发挥其目标导向作用，高校、科研院所为其提供人才、技术支撑、政府通过资金与政策为其提供基础保障。三是政府应利用物联网、云技术等搭建创新协作智能网络服务平台，通过该平台强化信息的互联互通机制，促进主体间知识共享，最终使其成为三方交流互动、发现合作机遇并展开协同创新的新高地。

(3)考虑到创新活动的空间溢出效应，应打破地域限制，强化区域间研发要素的流动。研发人员是知识、技术的载体。研发人员的区际交流互动、学习考察等均有助于吸收其他地区先进的经验，从而为本地区的创新发展提供借鉴。基于此，区域间可以建立公共研发联盟，联盟内的成员定期组织研发交流活动，通过这种方式，落后地区积极学习其他地区的先进理念和实践，可以减少地区间研发水平良莠不齐的现状。

此外，还应建立研发投入分类管理机制。我国地域广博，地区间发展呈现出显著的异质性和非均衡性特征。基于此，区域科研投入管理机制应因地制宜，而不是采取“一刀切”的简单方式。各地区依据自身的研发投入阶段性演化特征，科学判断研发资源的投入规模和强度。