信用风险对我国债券信用利差的贡献——基于债券面板数据的证据

陶雄华，郑肇晨，曹松威

(1.中南财经政法大学 金融学院，湖北 武汉 430073；2国信证券 博士后工作站，广东 深圳 518001)

一、引 言

我国经济正处于高速增长阶段向高质量发展阶段转变，在淘汰落后产能培育经济新动能时期出现经济增速有所放缓、企业盈利增速下滑的现象。很多企业在“去杠杆”的宏观政策背景下债务压力上升、流动性趋紧而导致近几年信用债市场上的违约风险集中暴露。我国债券市场的信用风险暴露经历了一系列结构性的变化，同时也是政府隐性担保预期逐渐被打破的过程。2011年至2014年间政府隐性担保对债券定价影响显著[1-2]，使信用违约风险未能有效反映到债券价格当中。2014年“11超日债”的违约标志着我国信用债市场的“刚兑”预期被打破，债券违约走向常态化[3-4]。2018年共120支债券违约，接近前4年的总和122支；2018年违约金额1176亿远远超过前4年的总和860亿元[5]。加快完善债券违约处置机制已是当务之急。虽然信用风险定价机制在逐步完善，但目前违约因素在多大程度上反映到债券价格当中，这个问题国内已有研究还缺少定量分析。

对于近年来我国信用风险多大程度上解释了信用利差的动态变动这一问题，本文在Nozawa[6]信用利差的方差分解方法基础上，利用2014Q1～2019Q1我国信用债面板交易数据，在控制住债券评级因素后，分析了这两部分对信用利差波动的贡献率及它们与不同评级债券之间的动态非线性关系。本文的主要创新在于两方面：一方面，本文定量分析了近年来我国信用损失对债券信用利差波动的贡献度；另一方面，本文在Nozawa[6]的基础上结合Duffee[7]对方差分解方法的改进，提高了各因素贡献比率度量的精确度。

二、文献回顾与研究假设

1.文献综述

从研究方法来看，由于债券违约和收益的预期在事前不可观测，以往研究通常借助债务的“结构模型”[8-15]或“简化模型”[16-18]，以及利用衍生品定价模型[19-21]来量化信用利差中的信用风险。但传统模型只关注企业违约风险，导致在校准历史数据后模型的结果显著小于高评级债券的真实信用利差，此现象被称为“信用利差之谜”[15]39。因此，研究早期关注债券信用利差中信用风险无法解释的部分。

早期研究除发现补偿投资者的预期信用损失之外，利差中往往还存在一部分很可观的风险溢价[22]。此溢价部分主要是债券的流动性风险和宏观市场流动性主导的[19]2246。越来越多研究表明，模型和数据上流动性风险对信用利差的影响显著[23-24]，甚至是主导因素[25]941。考虑到企业违约概率会随经济周期波动，从美国150年的长期数据来看，违约风险的溢价部分总体略高于违约损失[26]243。另外，利差中违约部分和非违约部分并非完全正交，也有相互影响的部分[20]886，[23]2231。

国内以往研究由于缺少债券违约数据，往往回避信用风险而直接考察其他单因素对信用利差的影响。如市场层面的流动性因素[27-30]、投资者情绪[31]、交易机制[32]；公司层面因素的研究有代理问题[33]、公司信用评级[34]、公司盈余管理[35]。综合来看，已有研究未得出一致性结论。国内文献对信用风险的度量上通常依赖债券评级或莫顿违约概率等替代变量。如此设定变量难免失真，且模型往往依赖对公司债券结构和公司违约选择的假设。在近年我国逐步“打破刚兑”情况下，需要补充完善信用风险对信用利差影响的研究基础。

2.假设提出

将信用利差分解为违约和流动性两部分是实证研究中通常做法。Longstaff 等人将企业债券利差分成违约部分(信用违约互换溢价)和非违约部分，各评级债券结果表明违约风险解释了半数以上的利差[19]2218。Dick-Nielsen等人从利差中分解出流动性风险部分，剩余利差归为信用风险部分，这种方法更直接地考察了流动性风险在各评级债券中的非线性影响[36]473。Gilchrist和Zakrajsek从经济周期波动的角度将信用利差分解为顺经济周期的债券超额收益和逆周期的公司违约风险[37]1701。Schwert综合比较了不同的分解方法[18]2218，[35]473，发现美国城投债违约风险溢价占信用利差的74%～84%[38]。Nowaza认为，对公司债券投资者而言，因债券票息率是固定的，对其未来现金流的冲击预期就来源于兑付其持有债券的违约风险和交易债券得到的风险溢价水平变化，而其方差分解结果表明，信用风险和风险溢价对信用利差动态波动的贡献度相近[6]2050。

相比于西方国家，我国债券市场建设起步较晚，投资者风险意识、评级制度等市场机制还不够健全[39]，政府隐性担保也长期存在并影响着债券市场的定价[1]162，这可能会削弱公司信用风险在债券利差中的反应。同时从2015年开始，中国股票市场发生了大幅度波动，宽松货币政策的调整等因素促进了债券市场的发展，投资者对债券市场的收益也进一步增加。据此，本文提出第一个假设：

H1：相较于信用风险，债券期望收益主导了我国债券信用利差的波动。

与内生于市场机制的信用评级行业不同，我国的信用评级行业是内生于制度设计和监管需求的[40]，发债企业和评级机构出现“合谋”的概率更大，企业所获得的评级的区分度也更低[41]，这导致了我国债券信用评级的膨胀[42]。随着2014年债券违约的不断出现，信用评级的动态调整不断增多，且相比于债券发行时的信用评级，信用评级的调整会带来显著的市场反应，同时上调和下调所带来的市场反应程度也不同[43]。据此，本文提出第二个研究假设：

H2：债券信用评级会影响信用损失预期和超额收益预期对信用利差的边际贡献。

三、研究设计

本文先建立滞后一期的向量自回归来分析不同评级之间的动态变化，然后估计债券信用损失和超额收益在此VAR模型条件下的长期回归系数，最后估计各因素在长期回归中拟合值的标准差来确定其对信用利差波动的贡献权重。

1.样本选取及数据来源

针对公司债违约事件发生频率小且不连续以及目前国内违约样本太少而导致信用风险难以测度的问题，本文选取债券发行人属于A股上市公司的债券样本，使用已有研究[37]1701，[6]2053均采用的KMV方法来估计债券发行主体的违约概率。2014年1月至2019年1月期间，450个上市公司发行了公司债共1621支(银行间交易所上市637支，上证、深证交易所上市984支)，其中在2017年后上市交易居多。样本区间内，筛选出有成交量的交易日在每个月取平均价格，最后得到有评级分类的债券月度截面交易数据共19 974笔。其中违约债券数据占176笔。本文数据来自国泰安和wind。

2.研究变量的选择

(1)样本时间段。2014年后公司债违约才开始常态化，所以，本文样本时间段设定为2014年1月至2019年1月共5年，债券距离到期时间Ti=[1,5]，从2014年开始设定为5，逐年递减。

(2)评级划分。国外研究以评级BBB为界将债券分为投资级(IG)和高收益(风险)级(HY)。但此划分并不适合我国实际情况，根据中国证券登记结算有限公司要求主体评级为AA 级(含) 以上债券才具备质押融资资格的规定，本文按发行主体评级将公司债分为两组：投资级债券组(AAA，AA+，AA)和高收益债券组(AA-，A+，A，BB+，C)。评级标准按照2019年1月最新主体评级为准。

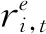
(4)违约样本。本文选取的债券违约类型包括：未按时兑付本金、利息、本息，担保违约，触发交叉违约及技术性违约。在规定时间段内去除短期融资券、中期票据及无交易日样本后，wind统计共有27支信用债违约，违约债券发行人除凯迪生态环境科技股份有限公司为公众企业外均为民营企业。

3.研究模型

(1)信用风险测度

由于我国存在债券评级虚高的问题，使用债券评级作为债券信用风险替代变量并不合理。本文参考Nowaza[6]2048对债券收益率的对数线性近似：

(1)

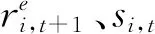
(2)

(2)各影响因素贡献比率

将(1)不断向前迭代至债券i的到期日Ti并取时间t的条件期望，得到信用利差的动态分解会计恒等式：

(3)

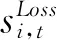
(4)

式(4)等号右边三部分分别与左边的比例就是各自对信用利差的波动相对贡献率。参照文献[44-45]中方差分解通常使用的VAR模型作为计算方差分解中条件期望的基础。假设单个债券i，服从滞后一期VAR模型：

Xi,t+1=A·Xi,t+Wi,t

(5)

其中因子向量：

(6)

dummyi是信用评级的虚拟变量，dummyi=(1,dAA+,dAA,d(AA-,A+,A,BB+,C))，本文将发行人主体评级AAA的债券作为参照组，对比其他3组不同评级。ti,tPDi,t是债券剩余期限与其发行主体的Merton模型预期违约概率乘积，研究一般在模型中加入此项来提高模型拟合度。模型假定Wi,t各期之间独立。

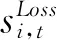
(7)

其中，ei是第i个元素，是1的m维单位列向量；ρ是接近于1常数。定义eL=-ρe2+e2A-1-e1，G(Ti)=A(1-ρA)-1(I-(ρA)Ti-t)。

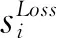
(8)

(9)

四、实证结果分析

1.变量的描述性统计

表1 各变量定义

表1 变量描述性统计分析

2.变量之间的相关性分析

以A股上市企业2014～2019年发行的债券月度交易数据为对象进行变量之间的Pearson相关性分析(表2)。由表2可知，债券超额收益与各评级债券信用利差显著负相关；债券超额收益、各评级信用利差、违约概率均与信用损失预期及超额收益预期显著相关。这为一阶VAR的相关关系提供了初步证据，月度债券超额收益与各评级债券信用利差显著负相关，因为利差扩大的原因是债券价格下跌，而下跌的债券会导致持有人当月产生负的资本利得，此关系反映到投资者的长期超额收益上也是如此。此外，大部分控制变量与超额收益预期和信用损失预期之间存在相关关系，说明本文选取了有效的控制变量债券评级，体现不同评级债券对信用损失预期及超额收益预期的非线性影响，可看到相关性随评级恶化不断增强。由KMV方法计算出的违约概率PDi,t和各评级债券信用利差总体显著正相关，从数据上来看，违约概率并不能较好反映出市场风险定价。

表2 Pearson相关性分析

3.VAR滞后一期回归结果分析

参照方差分解方法通常的设定[5]2052，[45]1259，模型假定不同债券在各期之间表现都一致，即VAR的系数矩阵A是恒定的，且债券间无个体效应。虽然系数矩阵A在各期恒定是个很强的假设，但恒定的系数矩阵条件为条件期望(3)向前迭代至债券到期日提供了便利，这也是VAR模型中去掉截距项的原因。另外，通过引入评级虚拟变量与利差交乘项后，可以在长期回归中体现出不同因素对各个评级的利差的非线性影响。

由于不存在债券之间的个体效应，使用混合最小二乘法来估计VAR模型(5)的系数矩阵A的各行。将4组评级债券放在一起查看信用评级从高到低对各因素影响的动态变化，如表3所示。

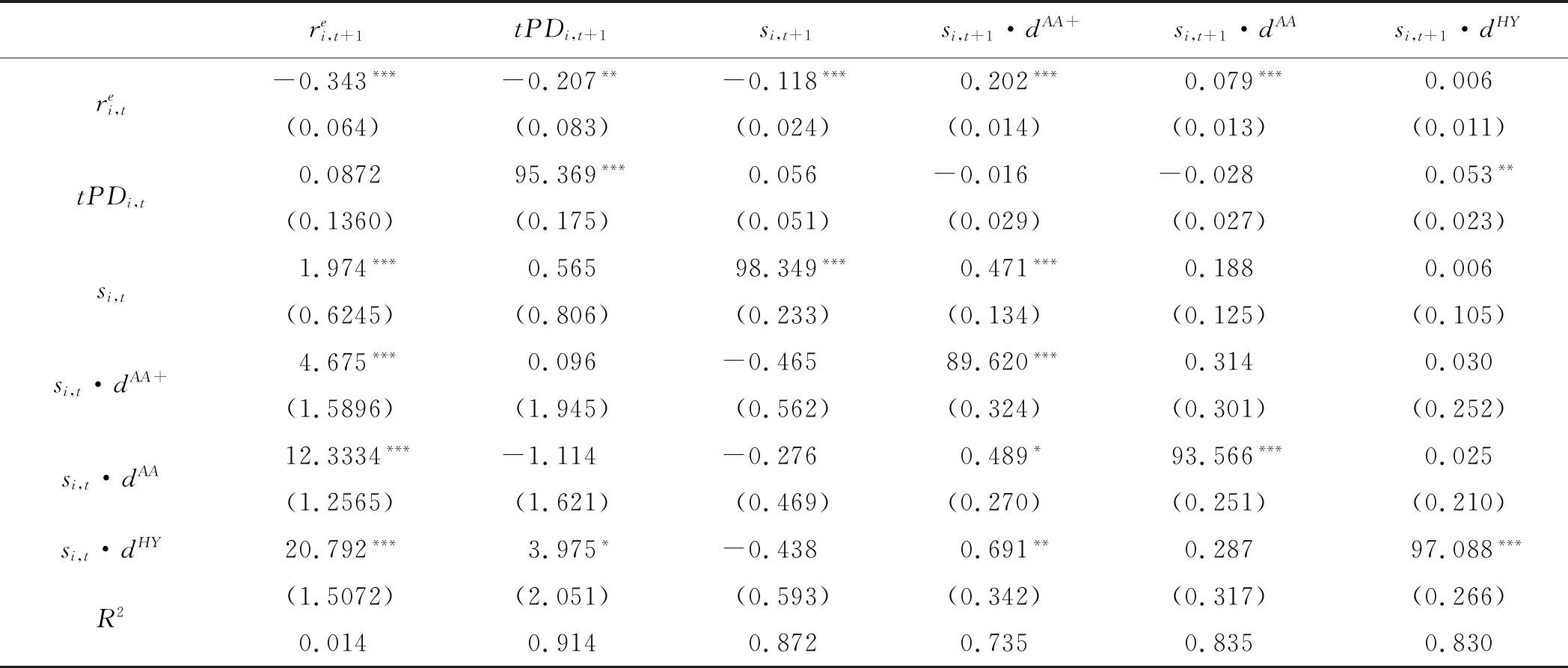
表3 一阶VAR系数估计

表3展示了VAR模型对各因子滞后一期的系数矩阵A的估计结果。此一阶VAR在方差分解方法中的作用更多是为了计算信用损失和超额收益的条件期望，并非为严格考察滞后一期向量自回归的系数的精确解释。具体而言，表格第一列估计结果说明在其他因素不变情况下，当期超额收益越小，信用利差越大，下期超额收益就会越高。

4.VAR长期回归结果分析

在回归模型中设定债券信用评级与其信用利差的交乘形式(si,t·di)是为了体现出各评级债券对预期信用损失和预期超额收益表的非线性影响。从表4的结果来看，在其他条件不变情况下，预期信用损失随评级债券下降对信用利差的边际贡献系数不断上升：基准组AAA债券是0.064个单位，AA+债券是0.50(0.064+0.434)个单位，AA债券是0.77(0.064+0.705)个单位，高收益债券组(AA-，A+，A，BB+，C)平均来看是0.80(0.064+0.740)个单位。而预期超额收益对信用利差的贡献则是边际递减。

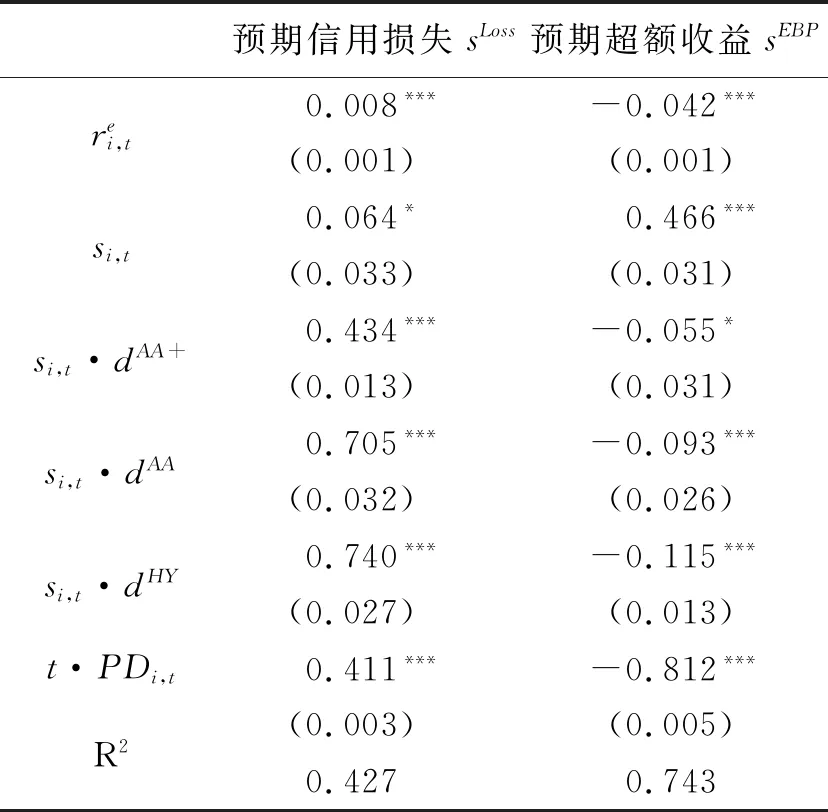
表4 各因素的长期回归

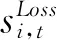
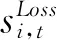
图1 各评级债券的信用风险和超额收益对信用利差的边际贡献注:图中横轴是信用利差，评级区间曲线斜率对应各评级债券的信用利差在长期回归中的回归系数；虚线是正/负标准差边界。

从表5结果来看，投资者的信用损失风险预期只贡献了27%的信用利差变动，而预期风险溢价贡献了48%的信用利差变动，所以，横截面信用利差波动主要是由债券期望收益因素推动而非信用损失预期。这一结论与国外等研究结果一致[15]，[22]273，[25]941，[26]243，[46]。

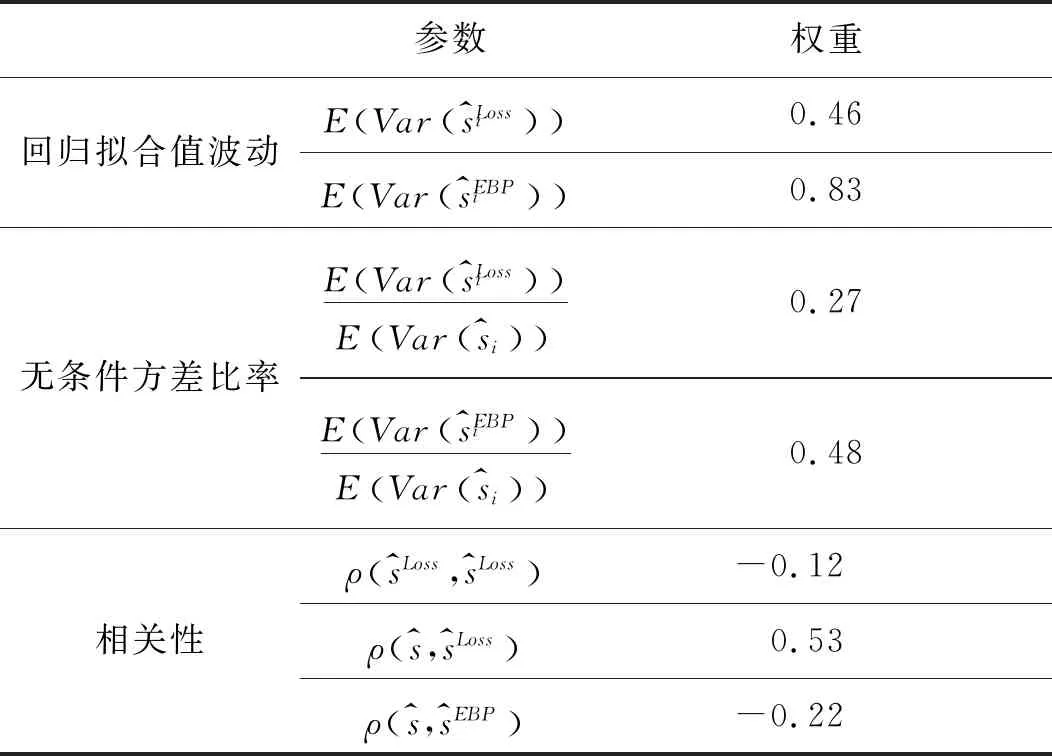
表5 方差分解结果及贡献权重

投资者预期信用损失因素占比偏小对于我国有特定的原因。一是信用风险并未完全反映到公司债定价中。正如纪志宏[29]提到的我国债券市场现状：由于存在政府的“刚性兑付”，投资者并未承担其信用风险，于是利用质押回购交易对信用债不断加杠杆。这也使得我们信用利差展现出很强的顺流动性周期，而非顺经济周期。流动性等交易层面的因素对信用利差的影响更大。二是我国公司债交易量太小且流动性极差，于是债券价格的波动更为剧烈，导致债券超额收益变动过大。

投资者的信用损失预期和超额收益预期一起贡献了75%的信用利差的变动，剩下的25%对应为方差分解式(4)的右边第三项cov(sLoss，sEBP)/σ(S)，即违约与非违约因素的相互影响解释了四分之一的信用利差波动。有文献专门对这部分因素交互影响进行了研究，实证了信用违约因素和流动性因素的相互影响部分对信用利差有显著正向影响[20]886,[23]2231(10%～24%)。预期信用损失序列和预期超额收益序列长期来看具有弱负相关性(-0.22)，说明预期违约风险越大的债券在超额收益上的预期越小。

五、结论与建议

基本所有信用债发行人都会向债券投资者支付一定高于无风险利率的溢价，以补偿贷款人的预期违约损失以及其他预期因素。以往通过结构化模型研究违约风险的文献往往需要对公司债券结构和违约选择进行假设，本文使用方差分解方法不需依赖模型假设，直接从债券交易数据和财务数据计算出投资者对信用损失与风险溢价的时变预期变化，并考察了它们对信用利差的解释程度。

利用我国上市公司在2014Q1至2019Q1发行信用债的月度交易数据得到以下结果：总体来看，债券的预期信用损失对公司债信用利差贡献偏小(27%)，而预期风险溢价是主导因素(48%)；从结构上来看，投资者对债券信用违约风险的预期对信用利差影响在AAA级最小，且随评级下降而递增；债券超额收益的预期对信用利差贡献在AAA级达到最大，但随评级下降而递减。

尽管我国从2014年后开始出现债券违约，但信用风险在债券信用利差中的作用并不明显。所以，首先，应继续打破“刚兑”预期，使违约逐步市场化、法制化。发挥我国信用债市场违约风险定价机制，使信用利差能更多反映信用状况的波动，让市场在资源配置中发挥决定性作用。其次，健全债券违约的配套处置机制。如建立到期违约债券转让机制，既可以保护债券投资者被动等待兑付的局面，又提高了违约债券处置效率。

本文基于会计恒等式方差分解方法的优势在于各组成部分的数量级可以直接依据数据估计出来，不需要依赖于具体信用模型或财务结构假设。但此方法受限于会计等式分解出来的变量，对于包含于变量其中及之外的因素无法考察，如杠杆率、交易机制、流动性等[2],[32],[47]。今后研究可将我国债券质押回购交易套利的杠杆[29]5行为纳入到在会计恒等式的方差分解框架下，进一步分析流动性及杠杆交易对债券定价的影响机制。