混凝土徐变对桥梁施工中挠度控制的影响研究

李 成

（中铁十九局集团第二工程有限公司，北京 100176）

0 引言

桥梁监控能够随时掌握桥梁施工时的受力情况，以确保施工质量以及安全性。在施工控制中线形控制是主要内容，而预拱度的设置是线形监控的主要内容。对于预拱度的设置而言，混凝土的徐变具有较大贡献。因此，正确确定混凝土的徐变效应对于混凝土桥梁的控制具有重大意义。

1 有限元分析

某工程的预应力混凝土连续刚构桥的跨径布置为44+88+44 m，桥梁上部为变截面箱梁，采用悬臂浇筑的施工方法。各节段混凝土的不断浇筑使桥梁施工时的荷载不断叠加。因为混凝土材料的不稳定性，使计算该桥梁的变形工作变得较为复杂。为确保桥梁施工时拥有科学的指导，需要在悬臂施工前以有限元分析的方式对该桥梁的应力以及位移进行监控，同时比较截面的应力和预拱度，以将其作为施工监控的依据。本文应用MIDAS/CIVIL 对该桥梁进行建模计算。模型中考虑了混凝土材料的徐变系数，并设置了桥梁预拱度。本项目选用的是国内相关规范中的徐变模型，时间与徐变系数的变化如图1 所示。

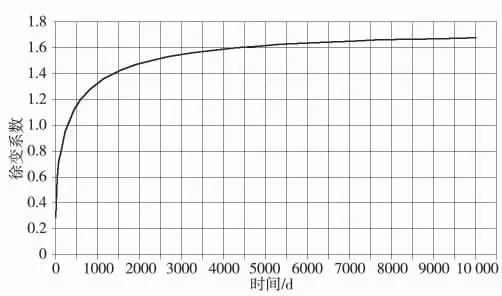
图1 混凝土徐变系数随时间的变化趋势

由于桥梁监控数据受温度的影响较大，因此应避免在高温时段监测桥梁的内力。该桥梁的应力监测时间为上午6:00～7:00以及傍晚的7:00 左右，桥梁的高程监测需在张拉弯预应力钢绞线以及悬臂浇筑后进行。部分监测结果见表1。

由表1 可知，模型计算的挠度值和实测值近似相等，不过以模型计算所得的挠度值比实测值要小，仅有部分数据偏大。综合分析后认为，导致这一情况的因素有混凝土的收缩续编以及温度应力等。为更加准确地预测桥梁施工时的线形，使模型计算结果更加准确，就需要对桥梁混凝土的容重、徐变等进行测试计算。

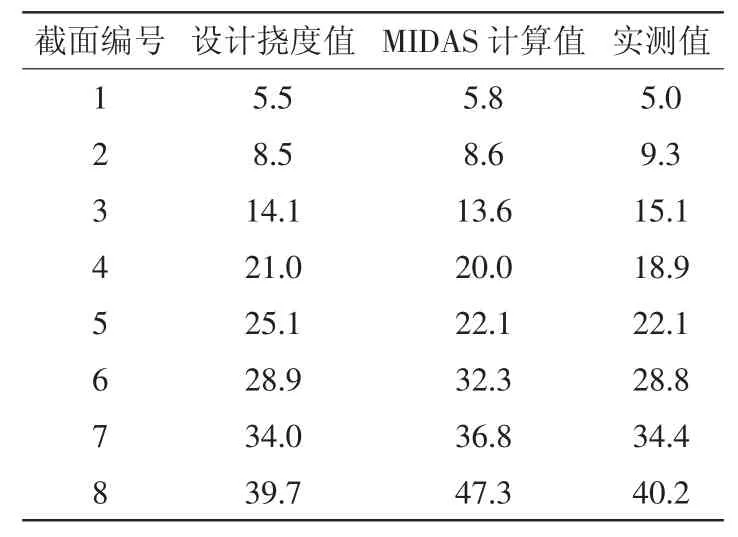
表1 桥梁挠度监测结果对比 mm

2 施工过程混凝土引起的挠度

2.1 混凝土徐变系数的计算

本文在计算混凝土徐变系数时，考虑了混凝土在加载时的不同龄期的固化程度以及环境因数等因素。混凝土加载时的龄期如图2 所示（仅列出部分计算图示）。

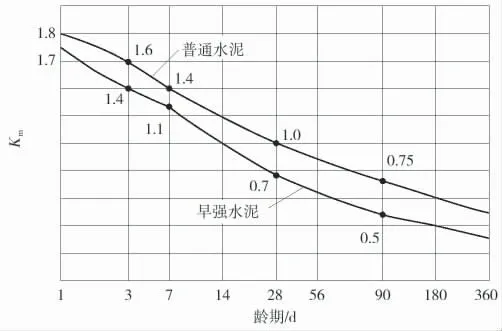
图2 混凝土加载时的龄期

在国内现有桥梁设计规范中，对混凝土收缩徐变模型有如下两种规定：一种是以滞后弹性变形加上塑性变形作为徐变系数的计算表达式，表示随着龄期的增加徐变系数不断增加的规定，此外在该规范中，还添加了混凝土加载时的强度以及加载龄期等相关的系数；一种是以名义徐变系数与相对应的时间跟徐变的函数表达式的乘积，在该规范中不再细分徐变，并增加了随着混凝土强度变化时徐变系数的变化规律，对于水泥品种以及温度则是以修正加载龄期的方式进行考虑。两种规范采用的是不同的量化规律。本文在计算混凝土徐变时采用的是第二种规范，所得结果如表2 所示。

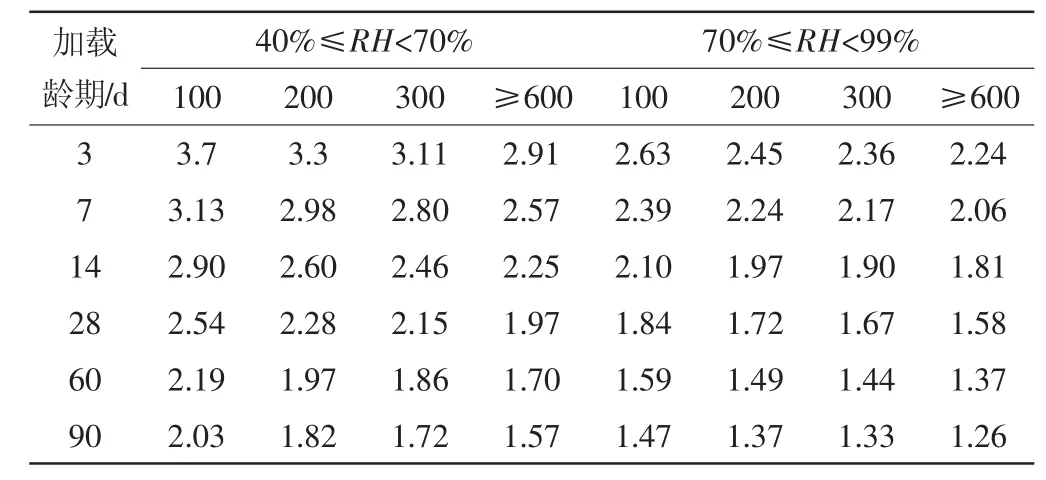
表2 混凝土徐变加载龄期与理论厚度h 的关系 mm

当桥梁所处地区的年平均相对湿度RH 在40%～70%时，RH 应取55%；当其所处区间为70%～90%时，应取80%。当桥梁构件加载龄期以及厚度为表中中间值时，可采用直线内插法的方式求取其混凝土名义徐变系数。

2.2 徐变计算式参数选取

徐变系数的选取可按照以下步骤进行：确定桥梁实际的年平均相对湿度值RH，按照实际加载龄期确定混凝土的徐变发展系数，根据表2 数据确定桥梁的名义徐变系数来求取桥梁的徐变系数（表3）。于该桥梁所处地区的年平均相对湿度，将RH取值确定为55%。

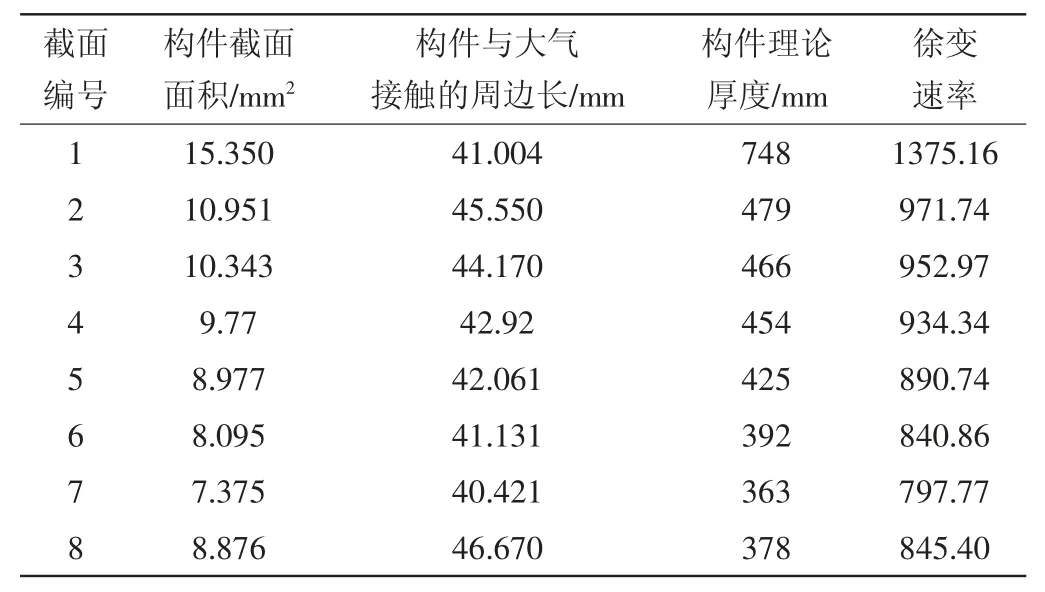
表3 徐变系数参数

按表3 中的徐变速率即可对其徐变系数间计算。因该桥梁混凝土的加载龄期均在90 d 以内，因此其名义系数可以通过直线内插的方式求取。

2.3 不同龄期混凝土松弛模量

在计算因混凝土收缩徐变所引起的挠度值以及桥梁变形值等都需要用到混凝土材料松弛模量参数。在试验现场开展混凝土弹性模量测试试验具有重要的意义。该试验可为混凝土桥梁施工时提供数据支撑，并且加深技术人员对混凝土强度变化的了解情况。

作为人工合成的混合材料，混凝土对桥梁结构的安全性有重大影响。但在实际工程应用时难以预测其相关性质。松弛模量作为混凝土重要的特性，其随着时间的推移会不断发生变化，并且具有较大的变异性。虽然国内已有混凝土松弛模量的验收标准，但施工期间混凝土的松弛模量值并无精确的取值。在工程实际中，鉴于施工条件不同，各个构件在某一时刻所处松弛模量与规范中的建议值并不相等，因此不能直接以规范进行取值。

混凝土的松弛模量与其所养护龄期等有关。在现场测试混凝土的松弛模量，可给施工监控提供参考以控制施工标高误差。并且，当前监测混凝土的受力状态主要是以应变传感器的方式实现，在将所测得的应变换算为应力时需将材料的模量值导入。要进行准确的换算必须要知道材料的模量变化规律。因此为了提高控制精度，需要对混凝土的模量值进行测试。在该项目中，选取了不同龄期的混凝土试块进行试验，样品数量为5。该种方法适用于完全样品数量在3～50 内的试验（图3）。

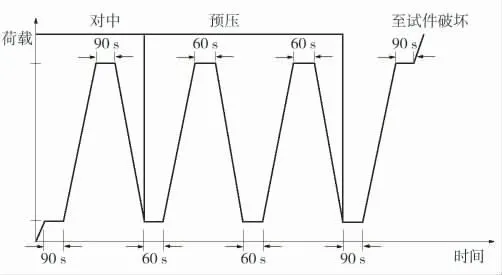
图3 模量试验加载流程

C50 混凝土在龄期为3 d、7 d、14 d、28 d 和355 d 时，实验得到的弹性模量分别为32.4 GPa、35.0 GPa、36.6 GPa、37.6 GPa 和34.3 GPa。在上述数据的基础上，假定混凝土松弛模量随时间呈指数分布，将两者关系绘制成图（图4）。

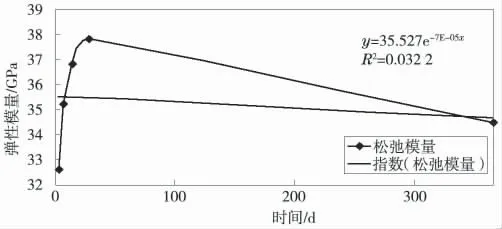
图4 混凝土松弛模量随时间变化趋势

2.4 结果对比

以上述结果分析张拉施工完成后因混凝土徐变所引起的挠度值，所得结果如表4 所示。

由表4 可知，与修正后的模型计算值相比，实算值修正后所得数据与实测值更加接近。以上述截面为例，其偏离程度最大的截面仅有9%的偏离率，而修正后的模型计算值却有12.5%的偏离率。以现场实际测量数据对徐变进行计算，所得到的挠度值具有较好的符合度。导致挠度出现偏差的因素有很多，其中主要是因为选取混凝土徐变系数时的误差导致的，在实际施工时应结合现场情况选取相应的徐变系数。

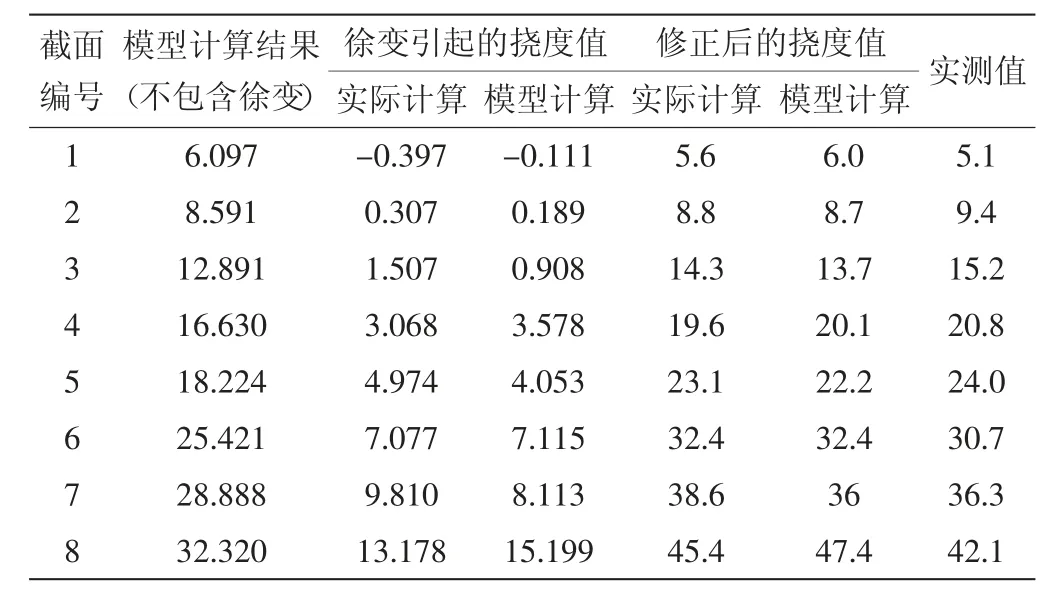
表4 施工阶段挠度对比 mm

3 结语

以上述分析可知，在桥梁的线形监控中，混凝土的徐变对其具有较大影响，必须采取相应的有效措施来降低混凝土徐变对线形的影响，使桥梁监控的准确性有所提高，确保桥梁成桥后线形控制效果良好。