交换半环上的广义正交矩阵

刘丽娟， 舒乾宇

（四川师范大学数学科学学院，四川成都610066）

半环，作为一种特殊的代数结构，于1894 年被Dedeking［1］在研究结合环的理想时提出，随后被许多 学 者 研 究［2-4］. 1979 年，Cuninghame - Green等［5］在min-plus 代数中构建了类似于经典线性代数的一系列理论.2007 年，Nola 等［6］在 MV - 代数上建立了半模，并得到了一些类似于经典线性代数中的结论.2010 年，Zhao 等［7］给出了 zerosumfree半环上的n 维半模中每组基有相同基数的充分条件；2011 年，Shu 等［8］给出了 zerosumfree 半环上的n维半模中每组基有相同基数的充要条件，并证明了一组向量为基当且仅当它是标准正交的. 2014年，Tan［9］给出了过渡矩阵的定义，并给出了交换半环上的有限生成自由半模中任意两个基有相同基数的等价条件；同年，文献［10］给出了交换半环上内积与正交集的定义，得到了一定条件下半域中标准正交集扩充为标准正交基的等价描述.众所周知，在经典线性代数中，标准正交基到标准正交基的过渡矩阵是正交矩阵，且任一正交向量组都能扩充成一组正交基.本文将研究交换半环中的正交矩阵，进而讨论有限生成半模中标准正交集的扩充问题.

1 预备知识

为了讨论方便，下面给出一些基本概念及已有的结论.

定义 1.1［2］半环 L ＝ 〈L，+，.，0，1〉是满足下述性质的代数结构：

1）（L，+，0）是交换幺半群；

2）（L，.，1）是幺半群；

3）对任意的 r，s，t∈L 满足 r.（s+t）＝r.s+r.t和（s+t）.r ＝ s.r+t.r；

4）对任意的 r∈L，有 0.r ＝ r.0 ＝0 成立；

5）0≠1.

特别地，若对任意的 r，s∈L，都有 r. s ＝ s. r，则称 L 是交换半环.对任意的 a，b∈L，若 a +b ＝0 蕴含 a ＝b ＝0，则称 L 是 zerosumfree 半环.

例1.1设N表示所有自然数构成的集合，则N连同普通加法和普通乘法运算构成一个交换的zerosumfree半环，记作 L ＝〈N，+，.，0，1〉.

定义 1.2［2］设 L ＝ 〈L，+，.，0，1〉为半环，M ＝（M，+M，0M）为一个加法交换幺半群.若外积*：L × M→M 满足对任意的 r，t∈L 和 α，β ∈M都有：

1）（r.t）*α ＝r*（t*α）；

2）r*（α+Mβ）＝r*α+Mr*β；

3）（r+t）*α ＝r*α +Mt*α；

4）1*α ＝α；

5）0*α ＝r*0M＝0M，

则称〈L，+，.，0，1；*；M，+M，0M〉为左 L-半模.

类似地，还可以定义右L -半模，其中外积的定义为M × L→M.在不引起混淆的情况下，在左L-半模 M 中，对任意的 r∈L，α∈M，将用 rα 来代替r*α.为方便起见，令＝ ｛1，2，…，n｝，其中 n为任意正整数.如无特别说明，下文中所指的半环均为交换半环，半模均为左L-半模.

例 1.2设L ＝〈L，+，.，0，1〉是半环，对n≥1，令其中（x1，x2，…，xn）T表示（x1，x2，…，xn）的转置.对任意的 x ＝ （x1，x2，…，xn）T，y ＝ （y1，y2，…，yn）T∈Vn（L）和 r∈L，定义运算如下：

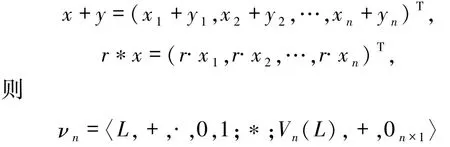
为L-半模，其中

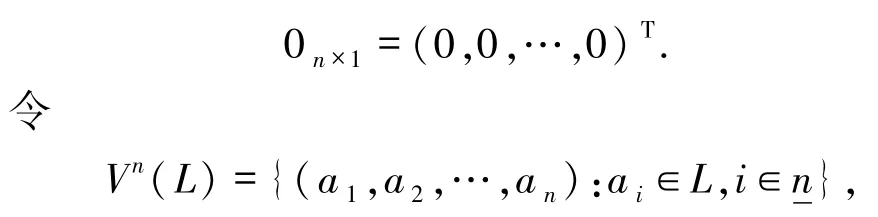
类似地，按以上方法来定义+和*，则

也为L-半模，其中

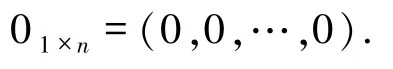
设A为L-半模M的非空集合.M中所有包含A的子半模的交集也是M 的子半模，称为由A生成的子半模，记为 Span（A）.易知

如果 Span（A）＝M，称 A 为 M 的生成集，称存在有限生成集的半模为有限生成半模，否则，称为无限生成半模.称M 的生成集中的最小基数n为M的秩，记为r（M）＝n.易知，任意有限生成半模的秩存在.

定义 1.3［10］设 A 为 L - 半模 M 的非空集合.若对任意的α∈A，有

则称A是线性无关的；否则，称A是线性相关的.若M中任意元素至多由A 中的元素唯一线性表出，则称A是自由的.

定义 1.4［10］设 M 为 L - 半模.称 M 中线性无关的生成集为M 的基，称M 中自由的生成集为M的自由基.

定义1.5［10］在 L -半模 M 上定义了一个二元运算〈，〉，称为M的内积，它具有性质：

1）〈α，β〉＝ 〈β，α〉；

2）〈λα +μβ，γ〉＝λ〈α，γ〉+μ〈β，γ〉，其中，α，β，γ∈M，λ，μ∈L.

例1.3在L-半模νn中，对任意的向量α ＝（a1，a2，…，an）T，β ＝ （b1，b2，…，bn）T∈Vn，α 和 β的内积记作〈α，β〉，等于它们对应分量的乘积之和

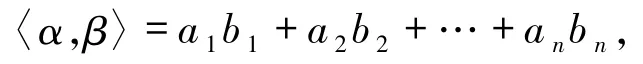
称该内积为νn的标准内积.

定义 1.6［10］设 M 为 L-半模，α，β∈M.若〈α，β〉＝0，则称 α、β 是正交的，记作 α⊥β.设 N 为M 的子集，若对任意的 α，β∈N，α≠β，α⊥β，则称N是正交的.若N是正交的，且对任意的α∈N，有

则称N是标准正交的.特别地，若〈α，α〉＝1，则称N是规范化正交的.

定义 1.7［10］设 M 为 L - 半模，称 M 中正交的（或标准正交的、规范化正交的）基为正交基（或标准正交基、标准基）.

例1.4在L-半模νn中，若考虑标准内积，则 ε1，ε2，…，εn是 νn的标准基，其中 ε1＝ （1，0，…，0）T，ε2＝ （0，1，…，0）T，…，εn＝ （0，0，…，1）T.

方便起见，下面将用 Mm×n（L）表示半环 L 上所有m×n矩阵构成的集合.特别地，令

对任意的 A ＝ （aij）m×n，B ＝ （bij）m×n∈Mm×n（L）和C ＝ （cij）n×l∈Mn×l（L），定义运算如下：

那么〈Mn（L），+，.，On，In〉为半环，其中同经典线性代数一样，在半模理论中，也能类似定义可逆矩阵、矩阵的转置、矩阵的迹等概念.

定义 1. 8［2］对任意的 A∈Mn（L），若存在B∈Mn（L）使得 AB ＝ BA ＝ In，则称 A 是可逆的，B为A的逆矩阵，记为B ＝A-1.

2 广义正交矩阵的定义及其性质

下面将给出广义正交矩阵的定义及其等价刻画.方便起见，先给出相关的记号.记

定义 2.1设 A ＝ （aij）∈Mn（L），若

则称A为广义正交矩阵.特别地，若ATA ＝In，则称A为标准正交矩阵.

引理 2.1［11］设 L 为半环，对任意的 A，B∈Mn（L）.如果 AB ＝ In，那么 BA ＝ In.

引理 2.2［12］设 L ＝ 〈L，+，.，0，1〉为 zerosumfree半环，若 A∈Mn（L）是可逆的，则 ATA、AAT都是可逆对角矩阵.

由定义2.1，有

命题2.1设A∈Mn（L）为广义正交矩阵，则下面结论成立：

1）A是可逆矩阵；

2）令 ATA ＝D，则 AD-1AT＝In；

3）（A-1）T为广义正交矩阵；

4）若 L 是 zerosumfree 半环，则 AT是广义正交矩阵；

5）若A是标准正交矩阵，B 是广义正交矩阵，则AB为广义正交矩阵.

证明1）若A∈Mn（L）为广义正交矩阵，由定义2.1 有

In＝（ATA）-1（ATA）＝［（ATA）-1AT］A.由引理2.1 知，A为可逆矩阵.

2）显然

因此，由引理2.1 有 AD-1AT＝In.

3）不妨设 ATA ＝D，则

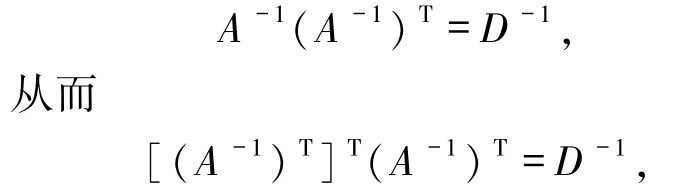
由定义2.1 知（A-1）T为广义正交矩阵.

由引理2.2 易知4）成立.

5）不妨设BTB ＝D，其中D为可逆对角阵，则

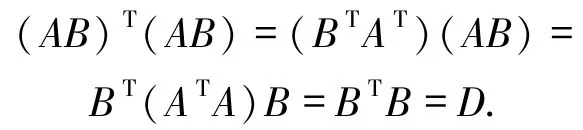
因此，AB为广义正交矩阵.

注 2.1i）一般情况下，即使 A∈Mn（L）为广义正交矩阵，A-1也不一定是广义正交矩阵.例如，在实数域R中，令则易验证A 为广义正交矩阵，然而却不是广义正交矩阵.

ii）值得注意的是，命题2.1 的5）中，若A为广义正交矩阵，B为标准正交矩阵，则AB不一定为广义正交矩阵.例如，在实数域R中，有

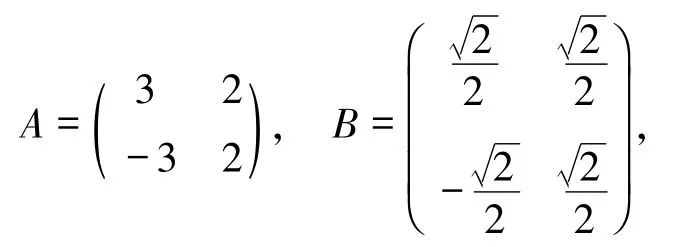
易知A为广义正交矩阵，B为标准正交矩阵，但

定义 2.2对任意的 A ＝ （aij）∈Mn（L），A 的主对角线上的元素之和称为A的迹，记为tr（A），即

定理 2.1设 A ＝ （aij）∈Mn（L），若 A 是广义正交矩阵，则：

1）tr（AAT）＝tr（ATA）＝d1+d2+… +dn；

2）ATA、AAT均为可逆矩阵，且

证明1）由定义2.2 知

2）易知ATA为可逆矩阵且

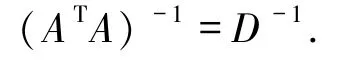
由命题 2.1 的 2）知 AD-1AT＝ In，则

因此，AAT

是可逆矩阵且

3）由

标准正交矩阵A 的转置AT与逆矩阵A-1均为广义正交矩阵，且A-1＝AT.然而，在一般情况下，此结论对广义正交矩阵却不一定成立.例如，在实数域R 中，令则那么

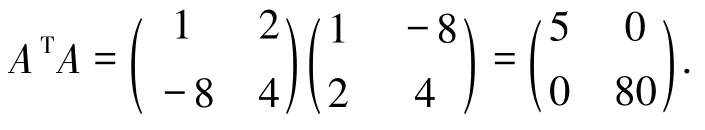
因此，矩阵A为广义正交矩阵.但

下面将在一些半环上给出广义正交矩阵的转置与逆矩阵为广义正交矩阵的充要条件.首先给出一些相关定义.

定义2.3［2］半环L中元素a 称为加法可消的，当且仅当对任意的 b，c∈L，由 a +b ＝ a +c可得b ＝c.用K+（L）表示半环 L 中所有加法可消元构成的集合.若 K+（L）＝L，则称半环 L 是加法可消的.

定义 2.4［2］在半环 L 中，设 W（L）＝｛a∈L：若 b∈L，则存在元素 r∈L 使得 a +r ＝ b 或 a ＝ r +b｝.若 W（L）＝L，则称 L 是 yoked半环.

定义2.5［2］设a为半环L中的非零元，若存在非零元b∈L 使得 ab ＝0，则称 a 是一个左零因子，而称b是一个右零因子.若一个非零元既是左零因子又是右零因子，则称之为零因子.

定义2.6［2］半环L 中元素a 称为乘法可消的，当且仅当对任意的 b，c∈L，由 ab ＝ac可得 b ＝c.

引理 2.3［2］设 L ＝ 〈L，+，.，0，1〉是加法可消的yoked半环，对任意的a∈L，若a是非零因子，则a是乘法可消的.

定理 2.2设 L ＝ 〈L，+，.，0，1〉是加法可消的 yoked 半环，A ＝ （aij）∈Mn（L）为广义正交矩阵，如果A满足条件：存在某一行和某一列的元素均为非零因子，那么下列条件等价：

1）AT为广义正交矩阵；

2）A-1为广义正交矩阵；

3）D1＝aIn，其中 D1＝ATA，a∈U（L）.

证明1）⇒3） 不妨设

由（1）式知

进而有

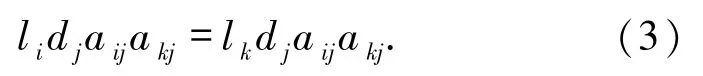
又L是yoked的，所以对任意的li、lk，存在r∈L使得 li+r ＝ lk或 li＝ r +lk.若 li+r ＝ lk，则由（3）式知

又L是加法可消的.因此

不妨设A 的第p 列的元素均是非零因子，由引理2.3知对任意的是乘法可消的，则由对任意的知 r ＝ 0.因此，li＝ lk，∀i，若 li＝ r+lk，类似可证不妨设不妨设A的第t行的元素全为非零因子，即对任意的为非零因子.由（2）式知

因为L是yoked的，所以对任意的dj、a，存在r∈L，使得 dj+r ＝ a 或 dj＝ r +a.若 dj+r ＝ a，则由（4）式知

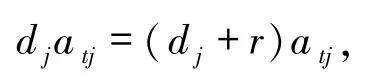
又 L 是加法可消的.因此，ratj＝ 0.由为非零因子可知 r ＝0，故若 dj＝ r +a，类似可证因此

3）⇒2） 由 ATA ＝D1＝ aIn，a∈U（L）知

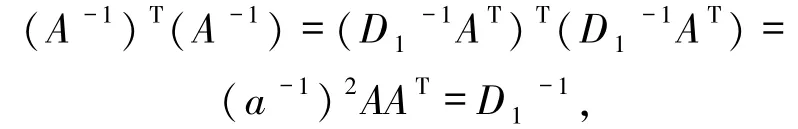
即A-1为广义正交矩阵.

2）⇒1） 不妨设（A-1）TA-1＝ D3，其中 D3为可逆对角阵，则

即AT为广义正交矩阵.

定义 2.7［10］设 M 为 L - 半模，若 M 的每个基有相同的基数，则称该基数为M的维数，记作dim（M）.

记 V（L）＝｛a∈L：存在 b∈L 使得 a +b ＝0｝.事实上，如果V（L）＝L，则L是环.

定义 2. 8［2］设 A ＝ （aij）∈Mn，σ 为排列的正行列式 ｜A ｜+和负行列式｜A｜-为：

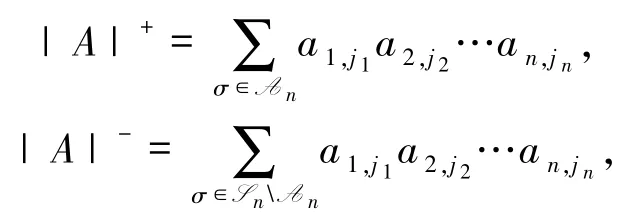
其中 Sn和 An分别表示｛1，2，…，n｝的对称群和交错群.若｜A｜-∈V（L），则 A 的行列式

若｜A｜+∈V（L），则

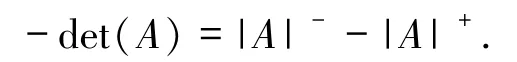
引理 2.4［13］设 L 为半环，dim（ν1）＝1，A ＝（α1，α2，…，αn）∈Mn（L），其中 αi＝ （a1i，a2i，…，那么A 是可逆矩阵当且仅当A 的列向量满足以下性质：

3）要么 det（A）存在，且 det（A）∈U（L），要么-det（A）存在，且 -det（A）∈U（L）.

令 V（L）2＝｛a∈L：存在 b，c∈V（L）使得 bc ＝a｝.

定理 2.3设 dim（ν1）＝1 且 V（L）2＝ ｛0｝，V（L）≠L.若 A ＝ （α1，α2，…，αn）∈Mn（L）满足条件：对任意的若

则A为广义正交矩阵当且仅当A可逆，其中

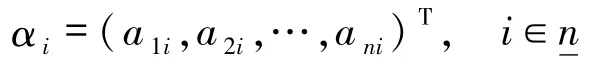
表示A的第i列.

证明由命题2.1 的1）知只须证明充分性.由引理 2. 4，不妨设 a11，a22，…，ann∈U（L），aij∈V（L），其中任意的由于 V（L）2＝ ｛0｝，所以故对任意的有

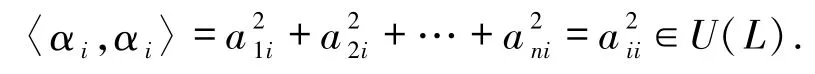
即A为广义正交矩阵.

推论 2. 1［13］设 L 是 zerosumfree 半 环，dim（ν1）＝1，若 A∈Mn（L），则以下条件等价：

1）A为广义正交矩阵；

2）A为可逆矩阵；

3）存在置换矩阵 Q∈Mn（L）使得QA 为可逆对角矩阵.

设 M 为 L-半模，｛β1，β2，…，βn｝为 M 的一组基，则对任意αj∈M，不妨设其中则

其中 A ＝（aij）∈Mn×m（L）.若｛α1，α2，…，αm｝为 M的一组基，称 A 为基｛β1，β2，…，βn｝到基｛α1，α2，…，αm｝的过渡矩阵.

在经典线性代数中，标准正交基到标准正交基的过渡矩阵为正交矩阵，在半模中是否也有类似的结论呢？讨论此问题之前，先给出相关的一些结论.

引理 2.5［10］在L-半模 M 中，若 r（M）＝n，则有

1）M中任意标准正交集的基数都不超过n；

2）M中任意基数为n的标准正交集是M的标准正交基；

3）若M有标准正交基，那么M 中任意基数为n的正交集是M的标准正交基.

如无特别说明，下面所指的L-半模均为存在标准基的有限生成半模.

定义 2. 9［10］设 A ＝ ｛α1，α2，…，αm｝，B ＝｛β1，β2，…，βn｝为L-半模M 的2 个非空子集.对任意的若 αi可以表示为 β1，β2，…，βn的线性组合，且对任意的可以表示为 α1，α2，…，αm的线性组合，则称A与B等价，记作A∽B.

引理 2.6［10］设 A ＝ ｛α1，α2，…，αm｝，B ＝｛β1，β2，…，βn｝为 L- 半模 M 的两个标准正交子集，如果A∽B，那么m ＝n.

引理 2.7［7］在 L- 半模 νn中，A∈Mn（L）为可逆矩阵当且仅当A的列向量为νn的一组基.

定理 2.4设｛ε1，ε2，…，εn｝为 L - 半模 M的一组标准基，若（α1，α2，…，αm）＝ （ε1，ε2，…，εn）A，其中 A ＝（aij）∈Mn×m（L），那么｛α1，α2，…，αm｝为M的一组标准正交基当且仅当A为广义正交矩阵且m ＝n.

证明必要性 若｛α1，α2，…，αm｝为标准正交基，由引理 2.6 知 m ＝ n.又｛α1，α2，…，αm｝是标准正交的，故对任意的 i，j∈n，

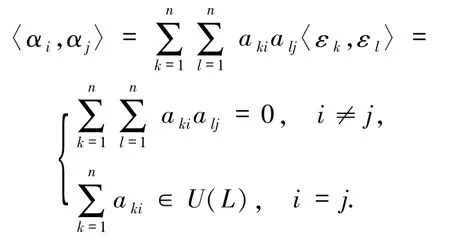
充分性 不妨设 ATA ＝ diag（d1，d2，…，dn），则有

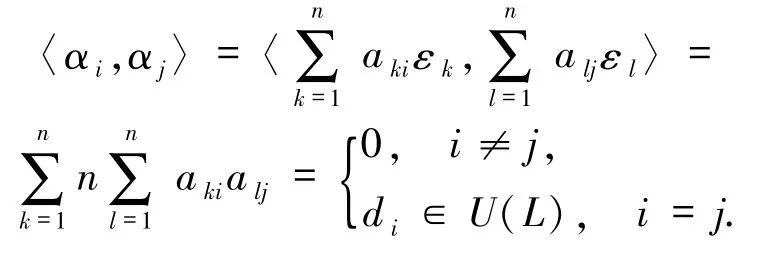
因此，｛α1，α2，…，αn｝为标准正交集.由引理 2.5可知｛α1，α2，…，αn｝为 M 的标准正交基.

由定理2.4 及其证明，有下面推论成立.

推论 2.2设｛ε1，ε2，…，εn｝为 L - 半模 M的一组标准基，若（α1，α2，…，αm）＝ （ε1，ε2，…，εn）A，其中 A ＝ （aij）∈Mn×m（L），则有

1）｛α1，α2，…，αm｝为 M 的标准基当且仅当A为标准正交矩阵；

2）｛α1，α2，…，αm｝是标准正交的当且仅当ATA为可逆对角阵；

3）若｛α1，α2，…，αm｝为 M 的标准正交集，则A的列向量组为L-半模νn的标准正交集.

定理 2.5设｛ε1，ε2，…，εn｝为 L - 半模 M的一组标准基，则

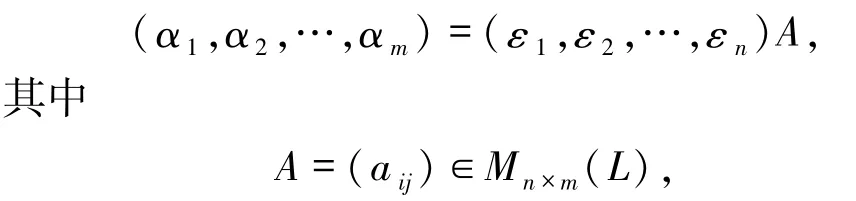
若｛α1，α2，…，αm｝为 M 的标准正交基，则 A 的行向量组为νm的一组自由基.

证明由定理2.4 和命题2.1 知A 为可逆矩阵，从而AT也为可逆矩阵，故存在B∈Mn（L）使得BAT＝In.不妨设 AT＝ （β1，β2，…，βn）.由引理 2.7知｛β1，β2，…，βn｝为 νn的一组基，下证｛β1，β2，…，βn｝是自由的.对任意的 β∈νn，若

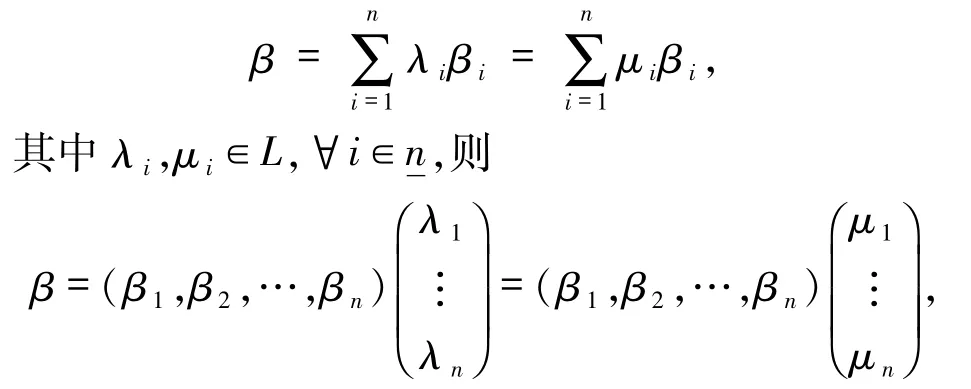
两边同乘矩阵B，则有

设 r（M）＝ n，值得注意的是，如果 A 为 M 的标准基到标准正交基的过渡矩阵，那A的行向量组不一定为 νn的标准正交基.因为A 为广 义正交矩阵，但AT不一定是广义正交矩阵，故AT的列向量组不一定为νn的标准正交基.

3 标准正交集的扩张

下面将讨论在L -半模M 中标准正交集扩充为标准正交基的充要条件.

定理 3.1设｛ε1，ε2，…，εn｝为 L - 半模 M的一组标准基，若

（α1，α2，…，αm）＝（ε1，ε2，…，εn）A， m≤n，

则 α1，α2，…，αm可以扩充为 M 的一组标准正交基当且仅当存在 ξm+1，…，ξn∈νn，使得

B ＝ （ξ1，…，ξm，ξm+1，…，ξn）

为广义正交矩阵，其中ξ1，…，ξm为A的列向量.

证明必要性 若 α1，α2，…，αm可扩充为 M的标准正交基，由引理2.6知，存在αm+1，…，αn使得α1，…，αm，αm+1，…，αn为 M 一组标准正交基.设

（α1，α2，…，αn）＝ （ε1，ε2，…，εn）B，

由定理2.4知，B为广义正交矩阵且B的第i列等于A 的第 i列

充分性 令

又B 为广义正交矩阵，故由定理2.4 知，α1，α2，…，αn为一组标准正交基，即 α1，α2，…，αm可扩张为M的一组标准正交基.

由定理3.1 和推论2.1 有如下推论.

推论 3.1设L 是zerosumfree半环，dim（ν1）＝1.令 ε1，ε2，…，εn为 L- 半模 M 的一组标准基，则M的任意标准正交集α1，α2，…，αm可以扩充为标准正交基，当且仅当存在对任意的存在唯一的使得 αi＝kiεji，其中 ki∈U（L）且对任意的若 i≠l，则 j≠jl.

引理 3.1［13］在半环 L 中，若 V（L）≠L 且dim（ν1）＝1，则 U（L）+V（L）＝U（L）.

引理3.2［14］设L为半环，那么

1）对任意的 a，b∈L，a+b∈V（L）⇔a，b∈V（L）；

2）对任意的a∈V（L），r∈L，有ra，ar∈V（L）.

定理 3.2设 dim（ν1）＝1 且 V（L）∩U（L）＝Ø.令｛ε1，ε2，…，εn｝为 L - 半模 M 的一组标准基，（α1，α2，…，αm）＝（ε1，ε2，…，εn）A，其中

A ＝ （aij）∈Mn×m（L）， m ＜ n，

则 α1，α2，…，αm可以扩充为标准正交基当且仅当A的每列的不同位置恰有一个乘法可逆元，其余元素全为加法可逆元.

证明充分性 不妨设 a11，a22，…，amm∈U（L）.首先证明存在 β 不能由 α1，α2，…，αm线性表出，其中

若任意这样的 β 均可由 α1，α2，…，αm线性表出，则存在 k1，k2，…，km∈L，使得

k1ai1+k2ai2+… +kmaim∈V（L），

由引理 3.2 和 aii∈U（L）知 ki∈V（L）.又因为

am+1，1，am+1，2，…，am+1，m∈V（L）.

因此，由引理 3.2 和（5）式知

k1am+1，1+k2am+1，2+ … +kmam+1，m∈V（L），

矛盾.设 γ 不能由 α1，α2，…，αm线性表出，其中

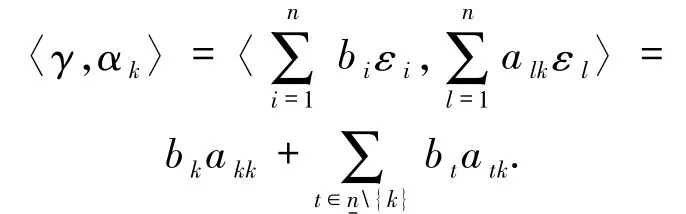
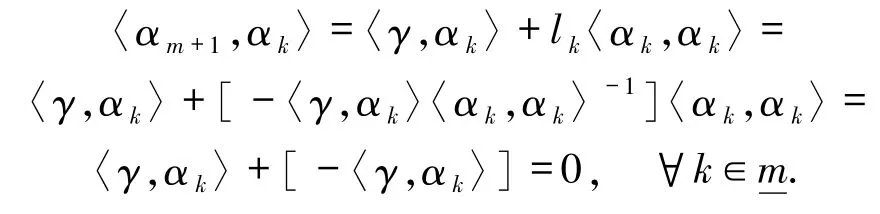
由（7）式有

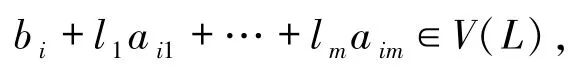
由引理3.1 知

则B的每列的不同位置恰有一个乘法可逆元，其余元素全为加法可逆元.若 α1，…，αm，αm+1是标准正交基，则结论成立，若 α1，…，αm，αm+1不是标准正交基，则重复以上证明过程可知 α1，α2，…，αm可扩充为M的一组标准正交基.

必要性 若 α1，α2，…，αm可扩充为 M 的标准正交基，由引理 2.6 知，则存在 αm+1，…，αn使得α1，α2，…，αn为 M 的一组标准正交基，故存在矩阵C∈Mn（L），使得

同理，由｛ε1，ε2，…，εn｝是 M 的一组标准基，故存在矩阵 B∈Mn（L），使得

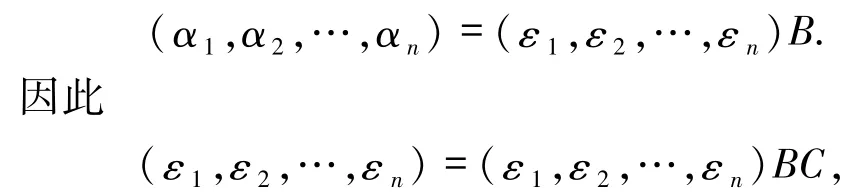
故BC ＝In.由引理2.1及引理2.4知B的每列的不同位置恰有一个乘法可逆元，其余元素全为加法可逆元，且对任意的有B的第i列等于A的第i列.

引理3.3［2］若1∈V（L），则 V（L）＝L.

定理3.3若半环L满足V（L）∩U（L）≠Ø，设 α1，α2，…，αn-1为 L - 半模 M 的标准正交集，若 r（M）＝ n，则必存在 αn使得 α1，α2，…，αn-1，αn为M的一组标准正交基.

证明若 V（L）∩U（L）≠Ø，则由引理 3.3 易知V（L）＝L.因为r（M）＝n，所以存在β∈M不能由｛α1，α2，…，αn-1｝线性表出，令

由 α1，α2，…，αn-1是标准正交的，则

故 α1，α2，…，αn-1，αn为 M 的正交集，由引理2.5知 α1，α2，…，αn-1，αn为 M 的标准正交基.

4 结论

本文给出了广义正交矩阵的定义及其等价刻画，并讨论了一类特殊的半环上有限生成半模中标准正交集扩充为标准正交基的充要条件.遗憾的是，一般交换半环上，标准正交集扩充为标准正交基的充要条件仍未能给出.