基于Dirichlet 模型的国内COVID-19 疫情数据的Bayesian 估计

杨云源， 杨新平， 张 洁

（1.楚雄师范学院地理科学与旅游管理学院，云南楚雄675000； 2.楚雄师范学院数学与统计学院，云南楚雄675000；3.楚雄医药高等专科学校，云南楚雄675000）

截至2020 -04 -10，全国 COVID -19 确诊83 369例，海外确诊1 537 039 例.疫情在美国、意大利、西班牙、德国等地急剧爆发.通过合理的数学模型，分别计算我国COVID -19 4 个概率指标（治愈概率、重症概率、病死概率、轻症概率）和4 个总量指标（累计治愈病例数、现有重症病例数、累计病死病例数、现有轻症病例数）的点估计及区间估计分别进行计算，以期为国内和海外COVID -19 疫情监测、指标估计和疫情阻断提供参考.

与治愈率、重症率、病死率、轻症率相关的研究，主要集中在疫情数据描述统计和疫情相关指标预测（估算）上.

1）疫情数据描述统计.如中华预防医学会COVID-19 防控专家组［1］基于截至 2020 -02 -10 的42 780 例确诊病例数据统计，指出COVID -19 病死率为2.38%，合并基础疾病的老年男性病死率较高.中国疾病预防控制中心COVID -19 应急响应机制流行病学组［2］对截至2020 -02 -11 的72 314例4 类病例的年龄、性别、旅居史等进行回顾性分析，揭示疫情自首次报告病例日后30 d 蔓延至31个省（区/市），粗病死率为2.3%.

2）疫情相关指标预测（估算），主要围绕再生数、感染规模、倍增时间等估算展开.如Wu 等［3］使用马尔科夫-蒙特卡洛法（MCMC）估算武汉COVID-19 再生数为2.68，流行倍增时间为6.4 d.陈端兵等［4］使用蒙特卡洛法（MC）依据少量患者的症状出现时间对有效再生数进行估计，表明我国在防控措施出台两周内，COVID-19 传播得到了有效遏制.其他方法如：使用 SEIR 或修正 SEIR 模型［5-7］、自回归移动平均模型（ARIMA）［8］、随机传输模 型［9］、最 大 似 然 法［10］、自 助 抽 样 法 （Bootstrap）［11］进行 COVID-19 疫情估算.以上文献中，文献［1 -2］基于病例数据的统计分析较全面，描述统计结果具有一定的可信度；模型使用中，主要针对再生数、感染规模等进行估算；参数确定直接关乎模型精度，如文献［5 -6］对相同研究区（湖北省、武汉市）使用相同方法，不同参数得到不同估算结果；文献［7］的疫情估算使用数据、方法较全面，首次使用了AI技术，预测国内疫情于4 月底结束.对于COVID-19 的治愈率、重症率、病死率、轻症率等重要指标，主要通过描述统计来量化，通过模型估计的较少.

Bayesian方法在医学运用方面，高文龙等［12］、张继巍等［13］分别简要介绍了 GeoBugs、OpenBugs在医学中的应用方法.贝叶斯方法可以量化给定数据条件下的不确定性参数值，借助先验信息和数据信息可提高数据分布参数的量化精度［14］.如 Yarnell等［15］将贝叶斯分析用于危重病医学中.Thall［16］将Bayesian方法用于癌症术后发病率估算与药物剂量确定.Li等［17］使用Bayesian方法来确定不同非药物疗法对失眠症的疗效和安全性的差异.

对疫情指标采用概率意义下的可信区间估计不仅能得到误差限而且精度高，有一定的实际意义.本研究根据国家卫建委2020 -01 -20 至03 -28 公报数据，建立 Bayesian 框架下的 Dirichlet 模型，通过MCMC 方法进行求解，得到逐日4 个概率指标（治愈概率、重症概率、病死概率、轻症概率）的点估计与区间估计，进一步计算逐日4 个总量指标（累计治愈病例数、现有重症病例数、累计病死病例数、现有轻症病例数）的点估计与区间估计，并进行误差分析，给出了估计误差限.以期研究方法与结果能为国内和海外COVID -19 疫情监测、指标估计和疫情阻断提供参考.

1 数据和方法

收集国家卫建委2020 -01 -20 至03 -28 公布的累计确诊病例数n、累计治愈病例数c、现有重症病例数e、累计病死病例数d数据.累计轻症病例为 m，则

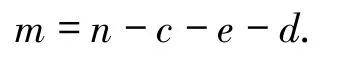
将 n、c、e、d、m 视为总体，第 t天的观测值分别记nt、ct、et、dt、mt.2020 -01 -20 至 01 -22 共 3 d 公报数据中的e1＝0、d1＝0，并且 3 d 的新增治愈数为0.所以本研究使用的样本数据为2020 -01 -23 至03 -28 共66 d的日报数据.

COVID-19 确诊病例逐日病情诊断、治疗康复出院前核算检测都需要一定的时间，加之前期检测试剂、医疗资源短缺，上报全国的疫情的各项日报指标值工作量较大.数据的误差可能是来自随机因素，也可能是系统误差，该误差不能消除，只能设法减小［18］，采用可信区间对COVID -19 疫情指标进行估计就变得更有实际意义.用带有一定误差的数据对治愈率、重症率、病死率、轻症率等相对指标进行计算，误差会累积，而Bayesian框架下的Dirichlet分布是解决此类问题的有力的工具.将国家卫健委公布的累记确诊病例数视为当日的独立试验次数（当日每个确诊病例病情变化视为一次实验过程），结合试验的结果（日报值），以多项分布为基础，建立Bayesian框架下的Dirichlet模型，借助数据信息及先验信息，通过Gibbs抽样方法得到总体参数的后验样本，采用MCMC方法得到治愈概率pt1、重症概率pt2、病死概率pt3及轻症概率pt4为参数的Bayesian 估计，进一步计算总量指标（治愈病例数、重症病例数、病死病例数、轻症病例数）的Bayesian点估计和区间估计.使用软件为Eviews、R语言和OpenBUGS.

2 Bayesian框架下的Dirichlet模型的建立

2.1 模型的建立将第t 天累计确诊病例数nt视为nt次独立试验，当日每个确诊病例的病情变化视为一次实验，每次试验有4 个互不相容的结果：At1＝“治愈”，At2＝ “重症”，At3＝ “病死”及At4＝“轻症”，且只有一种结果发生（无症状感染者日报起始于 2020 -04 -01），P（Ati）＝ pti，i ＝ 1，2，3，4.记待估参数为

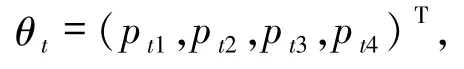
日报数据记为

由多项分布的定义有：

datat～ Multinomial（θt，nt），相应的似然函数为模型（1）

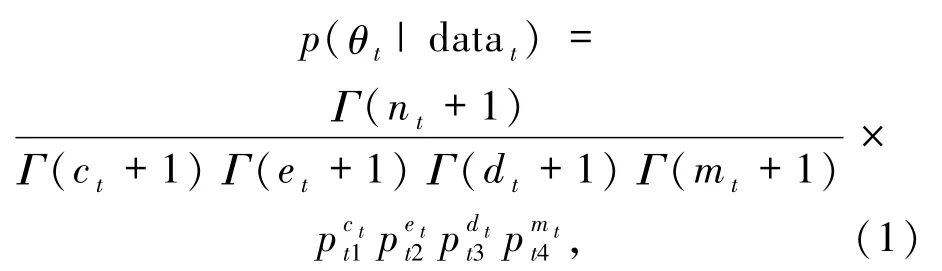
模型（1）中，

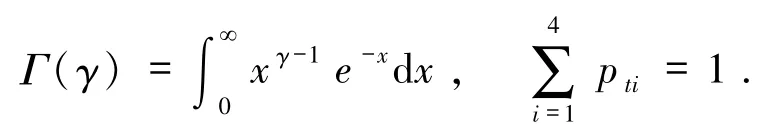
因为参数θt没有任何先验信息，按照 Nguyen的理论［19］，选择 Dirichlet 分布为其先验分布，第 t天先验分布模型为模型（2）

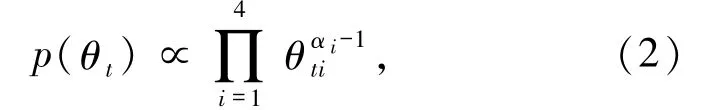
记 α ＝ （α1，α2，α3，α4）T，从而得到θt的后验精确分布

θt～ Dirichlet（α1+ct，α2+et，α3+dt，α4+mt），

相应的后验密度函数为模型（3）

模型（3）中，参数θt没有任何先验信息，根据Lunn等的理论［20］，对于先验分布 p（θt），选择 α ＝（1，1，1，1）T，该分布等价于四维的均匀分布作为θt先验分布.分别求出各个参数的满条件分布p（θti｜θt（-i），datat，α），其中，θt（-i）表示θt中 4 个分量去掉第i个分量后剩下的3 个分量构成的向量.比如

参数θt1相应的满条件分布为模型（4）

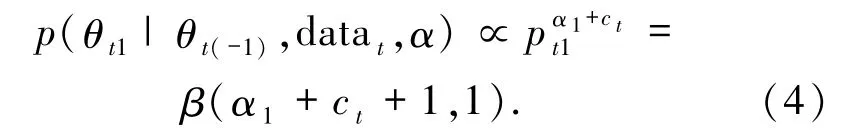
模型（4）是一个标准分布，其他3 个满条件分布与之类似，可以采用Gibbs 抽样得到全部参数（计 66 ×4 ＝264 个参数）的后验样本，形成 264 条MC链，完成Bayesian推断.

2.2 模型的求解在OpenBUGS 环境下进行模型求解.由于参数个数较多，设定随机数种子后，由软件自动生成参数的迭代初始值.为降低后验样本间的自相关性、同时又确保马氏链（MC 链）收敛，取间隔抽样步长为100，燃烧期为5 000，进行105次迭代Gibbs抽样，得到264 个待估参数的后验样本（264 条MC链）.扔掉燃烧期的前4 999 个样本后，用剩余的95 001 个样本通过MC 方法完成对参数θt的Bayesian推断，相应的参数估计值（表1）包括：均值估计标准差（σ）、MC 误差（εMC）、中位值估计（Median）及95% CI（可信区间）.同时将逐日 4 个参数（pt1、pt2、pt3及pt4各 66 个 Bayesian 估计）列表显示，表中“…”表示中间的行省略.

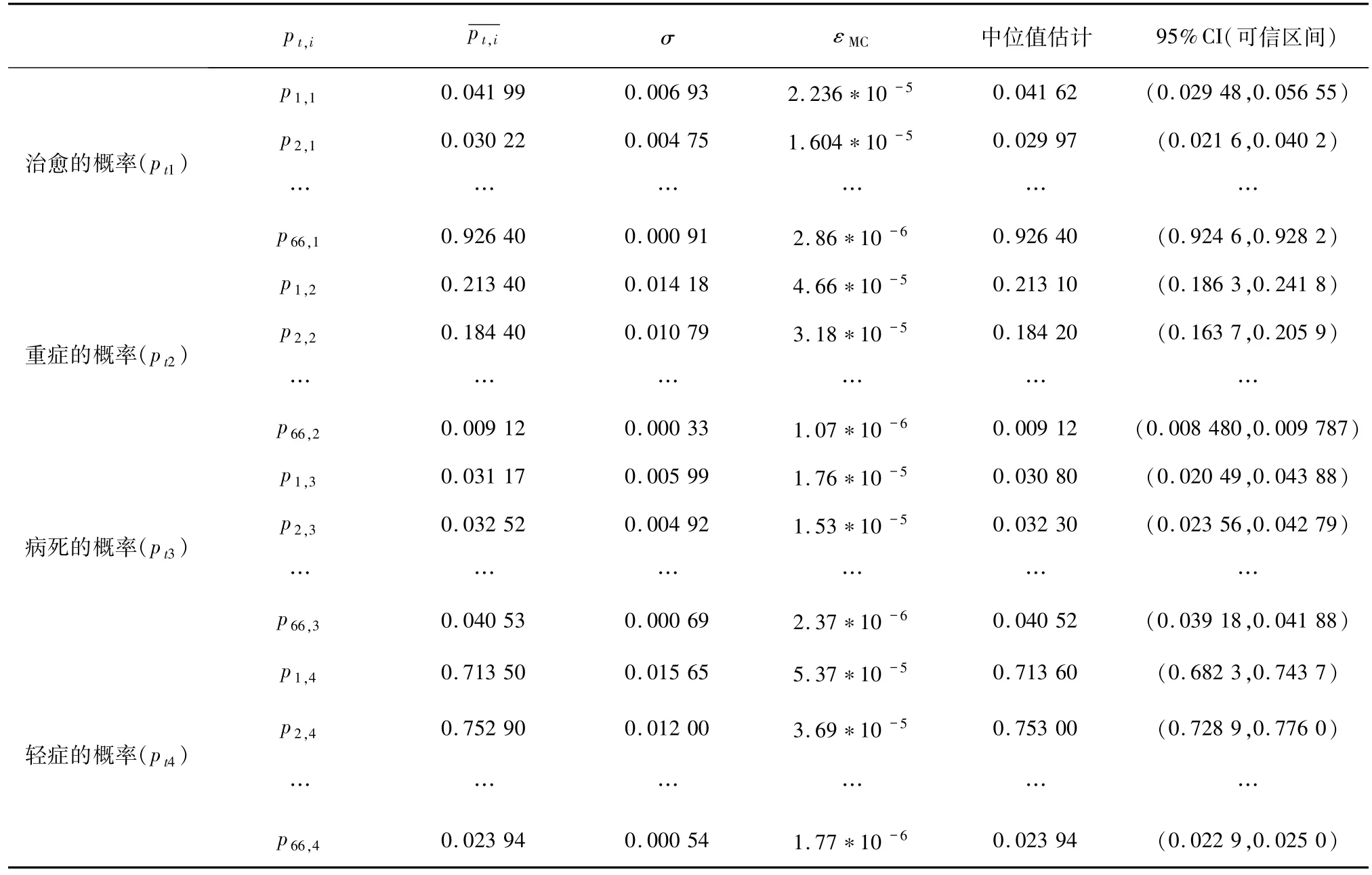
表1 参数θt的Bayesian估计及部分统计量汇总表Tab. 1 Summary of Bayesian estimation and partial statistics of θt

2.3 模型诊断对于模型（3）中的264 个参数，分别绘制History-strace-plot图、核密度估计曲线图和 Autocorrelation 图（以p1，1和p66，4为例，见图 1，其余的262 个图略，下同）. 264 个参数的 History -strace-plot 显示，前4 999 个燃烧值样本舍弃后，264 条MC链均收敛，且极限分布都是各自的后验分布，适宜用相应的MC 链作为后验样本进行统计推断.通过后验样本，分别求出参数pt，1至pt，4，t ＝ 1，2，…，66 的后验核密度估计（图 1 C -D，以p1，1和p66，4为例），结果显示参数的分布呈对称性，以正态分布为近似分布，后验均值与中位值几乎相等.每一条 MC 链的自相关图（图 1 E -F，以p1，1和p66，4为例）显示，在滞后期≥2 以后，自相关系数接近于0，所以每一条链均可视为独立同分布的MC 链，样本均值成为一致、有效、无偏的估计. 264 个参数的εMC均小于5.37 × 10-5. pt1、pt2、pt3及pt4最大εMC对应的相应数据信息见表 2.表 2 中（max｛εMC｝／σ）×100%最大值仅为0.774 55%，说明模型（3）具有较高的精度［19］.最大的εMC发生的时点均是2020 -01 -23，最大εMC对应4 个概率全部集中在2020 -01 -23；而且在2020-02-13前，样本计算得到的指标数据波动较大，后期逐渐光滑.说明2020 -02 -13前的日报数据误差明显大于后面的日报数据误差，再次说明区间估计的重要性.由各自的可信区间计算得到pt1、pt2、pt3及pt4点估计的最大误差限分别是0.013 535、0.027 7、0.011 695 及 0.030 7，预测误差最大发生的时点也是2020 -01 -23.

图 1 参数p1，1和p66，4的 History-strace-plot图、核密度估计曲线和 Autocorrelation 图Fig. 1 History-strace-plot，Kernel density estimation curve and Autocorrelation of parameters p1，1 and p66，4

表2 模型（3）的各条MC链的最大MC误差及相应数据信息汇总表Tab. 2 Summary of maximum MC error and corresponding data information of each MC chain of Model（3）

采用概率意义下的可信区间对疫情指标进行估计，精准性更高.它不仅给出每个日报指标的下限，而且给出上限及误差信息，同时，可信区间能覆盖指标的直实数据值.为此，利用模型求解过程中得到了264 条MC链（每条链都收敛于各自的后验分布），采用MC 方法得到相应参数的估计及统计量.然后提取逐日4 个概率的2.5%的后验分位数和97.5%的分位数绘制各自95%的可信区间，从而得到逐日4 个概率的95%的可信区间带.

3 结果与分析

3.1 治愈概率 、重症概率、病死概率及轻症概率估计本文2.3 模型诊断结果，充分说明模型（3）对于疫情的相对指标（4 个概率）估计的合理性与精确性，为了进一步将模型（3）的估计结果（概率）和样本计算的结果（频率）作对比分析.记fti（i ＝1，2，3，4）分别表示第 t 天样本计算的治愈频率、重症频率、病死频率和轻症频率.第 t 天相应概率Dirichlet模型（3）计算得到的中位值估计（ptif），数值结果见表 1，分别用qtil和qtiu（i ＝1，2，3，4）分别表示概率ptif的95%的可信区间的下限和上限，并用计算结果绘制相应的频率，概率曲线及95%可信区间带（图2）.

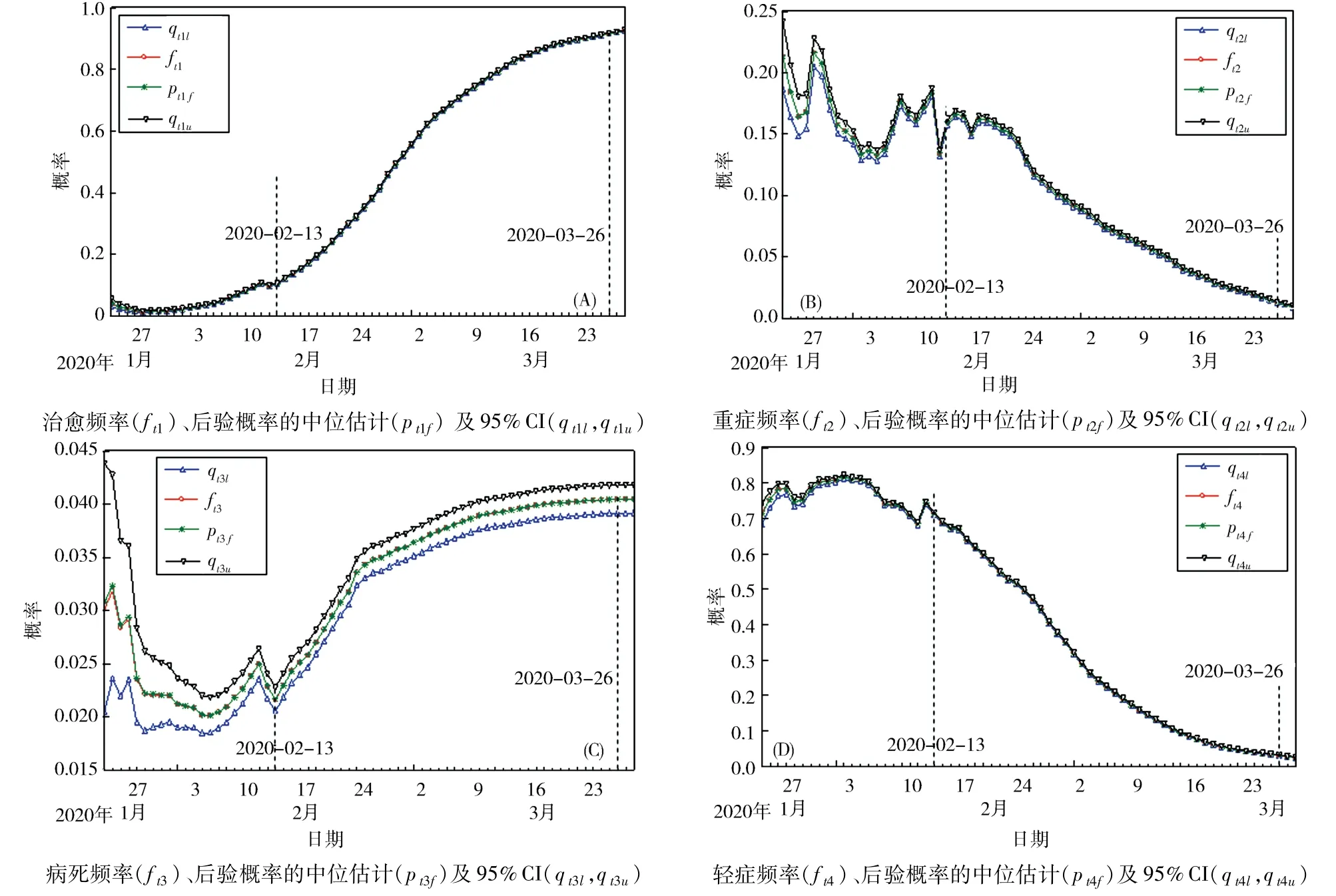
图2 治愈频率、重症频率、病死频率、轻症频率及对应的后验概率估计Fig. 2 Cure frequency，severe frequency，fatal frequency，mild frequency and the corresponding posterior probability estimation

结果显示：1）同一天的4 个概率和为1；2）除病死概率的可信区间带略宽，预测误差略大外，其他三者的可信区间带较窄，几乎与预测值曲线重叠，精度较高；3）4 个概率曲线在02 -14 后均呈现出光滑变化特性；4）治愈概率、重症概率、病死概率及轻症概率基本上呈现3 个阶段的变化特征.第一阶段（2020 -01 -23 至02 -13）治愈概率经历短期下降后缓慢上升，在2020 -02 -11 呈现小幅振荡；重症概率在幅度为2.8% ～24.2%的范围内振荡；病死概率在幅度为1.84% ～4.39%的范围内剧烈振荡；轻症概率在幅度为68% ～82%的范围内振荡.第二阶段（2020 -02 -14 至03 -26）治愈概率呈S型曲线逐渐上升，重症概率在2020 -02 -16经过小幅振荡后逐步下降，前期（02 -14 至02 -21）下降速度慢度，后期（02 -21 以后）下降速度稍快；病死概率前期（02 -14 至02 -23）上升速度比后期（02 - 23 以后）快，变化范围为 2. 18% ～4.18%，可信带稍宽；轻症概率呈反S 型曲线逐渐下降.第三阶段（03 -26后），治愈概率上升到92%以上；因为疫情得到控制，大量治愈病人出院，医院滞留病人快速减少，重症概率降到1.2%以下，且呈减少趋势；病死概率稳定在4%左右；轻症概率下降到3%以下，并趋于稳定.

3.2 累计治愈病例数、现有重症病例数、累计病死病例数、现有轻症病例数估计为简化公式，记

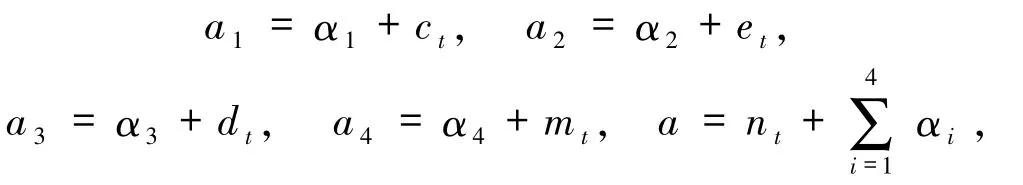
由Dirichlet分布的性质可知

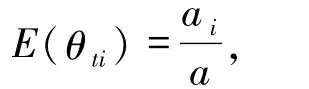
由K-Pearson替换原理，将各自的总体期望用后验均值估计替代，可得第t 天总体总量指标的Bayesian估计，分别记为累计治愈病例数估计ctf，现有重症病例数估计etf，累计病死病例数估计dtf，累记轻症病例数估计（记为mtf）.并借助表1 中概率的可信区间上下限，进一步求各个总体总量指标的95%的可信区间（下限、上限分别在相应符号后加l、u表示.如：累记治愈数95%的可信区间记为95%CI：（ctl，ctu），下同）.将 4 个总量指标点估计及区间估计绘制曲线图（见图3）.

图3 4 个总量指标估计及对应的95%可信区间Fig. 3 Four total quantity indexes and corresponding 95% confidence interval

结果显示：

1）除累记病死病例的可信区间带略宽，预测误差略大外，其他三者的可信区间带较窄，几乎与估计值曲线重叠，精度较高，而且上述四条可信区间带全部覆盖了样本值.

2）累计治愈人数和累计病死人数呈S 型曲线变化.表明医院治愈病例快速增加，后期进入对重症集中救治攻坚阶段.两个指标趋于稳定，略呈上升趋势.重症病例数以2020 -02 -18 为分界，前期为增长阶段，含 3 个振荡时点（02 -07、02 -12、02 -16），间隔期分别为5 d.后期为下降阶段，下降速度慢于前期的增长速度.轻症病例数以2020 -02 -16 为分界，前期为增长阶段，含一个跳跃时点（02 -12）.该值是第四版诊疗方案向第五版诊疗方案过渡，临床病例并入确诊病例产生.后期为下降阶段，下降速度慢于前期的增长速度.

3）将图3 中的4 组数据分别提取出来进行对比分析，发现绝大多数时点的Bayesian 点估计和样本观测值几乎一样，误差也较小.

为了反映总量指标的预测精度，将累计治愈病例数、现有重症病例数、累计病死病例数和累记轻症病例数预测误差限最大的4 个时点及对应的值提取出来汇总成表（表3），其他时点的预测误差限均比该时点的误差限小.

结果显示：这4 个指标的点估计的最大预测误差限为277.141 例，相应的指标是2020 -02 -25的轻症病例数（样本值36 852例）.

表3 4 个总量指标预测误差限最大的时点及对应值Tab. 3 Time and corresponding values of the maximum prediction error limit of four total quantity indexes

66 d逐日4 个指标，共计264 个点估计值，528个区间估计值（下限，上限），无法在一个表中呈现.以样本截止日2020 -03 -28 的计算结果为例（表4）进行说明.结果显示：点估计和样本值几乎相等，95%CI的上下限之差，点估计误差限都很小，充分说明用可信区间进行疫情的估计更为合理.

表4 2020 -03 -28 的4 个总量指标Bayesian估计及误差Tab. 4 Bayesian estimation and error of four aggregate indicators on March 2020 -03 -28

4 结论与展望

建立Bayesian框架下的Dirichlet 模型，借助样本和先验信息，通过Gibbs 抽样方法得到总体参数的后验样本，采用MCMC方法计算得到264 个模型参数的Bayesian 估计，即逐日4 个概率指标（治愈概率、重症概率、病死概率及轻症概率）的点估计及区间估计；使用Dirichlet 分布的性质进一步计算4个总量指标（累计治愈病例数、现有重症病例数、累计病死死病例数、现有轻症病例数）的点估计及区间估计.在Dirichlet模型求解过程中，264 个参数对应264 条 MC 链均收敛，最大εMC仅为标准差的0.775%，且极限分布都是各自的后验分布，适宜用相应的MC 链作为后验样本进行统计推断.计算了2020 -01 -23 至03 -28 逐日4 个概率（治愈概率、病死概率、重症概率、轻症概率）的点估计（共264个值）和95%区间估计（共528 个值）；治愈概率、病死概率总体呈现上升后趋于平稳趋势，重症概率、轻症概率总体呈现逐渐下降趋势；2020 -03 -26 后4 个概率指标都趋于平稳.计算了2020 -01 -23 至03 -28 逐日4 个总量指标（累计治愈病例数、现有重症病例数、累计病死病例数、现有轻症病例数）的点估计与95%区间估计.4 个总量指标点估计的最大预测误差限为277.141 例，对应的指标是2020 -02 -25 的现有轻症病例数（样本值368 52例）.截至2020 -03 -28，累计治愈病例数、现有重症病例数、累计病死病例数、现有轻症病例数点估计误差限分别为 146. 595、53. 100 8、109.948、85.515 例，对应的95%区间估计分别为：（75 301.20，75 594.39）、（689.881 0，796.082 6）、（3 189.937，3 409.833）、（1 864.045，2 035.075）.

用Bayesian框架下的Dirichlet模型计算逐日4个概率（治愈概率、病死概率、重症概率、轻症概率）的点估计与区间估计；计算逐日4 个总量指标（累计治愈病例数、现有重症病例数、累计病死病例数、现有轻症病例数）的点估计与区间估计，各自的计算精度均很高.Bayesian 方法还可广泛运用于更广泛的领域.